2.3: Tathmini, Kurahisisha, na Tafsiri Maneno (Sehemu ya 1)
- Page ID
- 173412
- Tathmini maneno ya aljebraic
- Tambua maneno, coefficients, na kama maneno
- Kurahisisha maneno kwa kuchanganya maneno kama hayo
- Tafsiri misemo ya neno kwa maneno ya algebraic
Kabla ya kuanza, fanya jaribio hili la utayari.
- Je\(n ÷ 5\), ni usemi au equation? Ikiwa umekosa tatizo hili, kagua Mfano 2.1.4.
- Kurahisisha\(4^5\). Ikiwa umekosa tatizo hili, kagua Mfano 2.1.6.
- Kurahisisha\(1 + 8 • 9\). Ikiwa umekosa tatizo hili, kagua Mfano 2.1.8.
Tathmini Maneno ya Aljebraic
Katika sehemu ya mwisho, sisi rahisi maneno kwa kutumia utaratibu wa shughuli. Katika sehemu hii, tutaweza kutathmini maelezo-tena kufuatia utaratibu wa shughuli.
Kutathmini kujieleza algebraic ina maana ya kupata thamani ya kujieleza wakati variable ni kubadilishwa na idadi fulani. Ili kutathmini maneno, tunabadilisha nambari iliyotolewa kwa kutofautiana katika kujieleza na kisha kurahisisha maneno kwa kutumia utaratibu wa shughuli.
Tathmini\(x + 7\) wakati
- \(x = 3\)
- \(x = 12\)
Suluhisho
- Kutathmini, badala\(3\) ya\(x\) kujieleza, na kisha kurahisisha.
| \(x + 7\) | |
| Mbadala. | \(\textcolor{red}{3} + 7\) |
| Ongeza. | \(10\) |
Wakati\(x = 3\), maneno\(x + 7\) ina thamani ya\(10\).
- Kutathmini, badala\(12\) ya\(x\) kujieleza, na kisha kurahisisha.
| \(x + 7\) | |
| Mbadala. | \(\textcolor{red}{12} + 7\) |
| Ongeza. | \(19\) |
Wakati\(x = 12\), maneno\(x + 7\) ina thamani ya\(19\). Kumbuka kwamba tulipata matokeo tofauti kwa sehemu (a) na (b) hata kama sisi ilianza na kujieleza sawa. Hii ni kwa sababu maadili yaliyotumiwa\(x\) yalikuwa tofauti. Tunapotathmini usemi, thamani inatofautiana kulingana na thamani inayotumiwa kwa kutofautiana.
Tathmini:\(y + 4\) wakati
- \(y = 6\)
- \(y = 15\)
- Jibu
-
\(10\)
- Jibu b
-
\(19\)
Tathmini:\(a − 5\) wakati
- \(a = 9\)
- \(a = 17\)
- Jibu
-
\(4\)
- Jibu b
-
\(12\)
Tathmini\(9x − 2\), wakati
- \(x = 5\)
- \(x = 1\)
Suluhisho
Kumbuka\(ab\) ina maana\(a\) mara\(b\), hivyo\(9x\) ina maana\(9\) nyakati\(x\).
- Kutathmini maneno wakati\(x = 5\), sisi badala\(5\) ya\(x\), na kisha kurahisisha.
| \(9x - 2\) | |
| Mbadala\(\textcolor{red}{5}\) kwa ajili ya x. | \(9 \cdot \textcolor{red}{5} - 2\) |
| Kuzidisha. | \(45 - 2\) |
| Ondoa. | \(43\) |
- Kutathmini maneno wakati\(x = 1\), sisi badala\(1\) ya\(x\), na kisha kurahisisha.
| \(9x - 2\) | |
| Mbadala\(\textcolor{red}{1}\) kwa ajili ya x. | \(9 \cdot \textcolor{red}{1} - 2\) |
| Kuzidisha. | \(9 - 2\) |
| Ondoa. | \(7\) |
Kumbuka kwamba katika sehemu (a) kwamba sisi aliandika\(9 • 5\) na katika sehemu (b) sisi aliandika\(9(1)\). Wote dot na mabano hutuambia kuzidi.
Tathmini:\(8x − 3\), wakati
- \(x = 2\)
- \(x = 1\)
- Jibu
-
\(13\)
- Jibu b
-
\(5\)
Tathmini:\(4y − 4\), wakati
- \(y = 3\)
- \(y = 5\)
- Jibu
-
\(8\)
- Jibu b
-
\(16\)
Tathmini\(x^2\) wakati\(x = 10\).
Suluhisho
Sisi badala\(10\) ya\(x\), na kisha kurahisisha kujieleza.
| \(x^{2}\) | |
| Mbadala\(\textcolor{red}{10}\) kwa ajili ya x. | \(\textcolor{red}{10}^{2}\) |
| Tumia ufafanuzi wa exponent. | \(10 \cdot 10\) |
| Kuzidisha | \(100\) |
Wakati\(x = 10\), maneno\(x^2\) ina thamani ya\(100\).
Tathmini:\(x^2\) wakati\(x = 8\).
- Jibu
-
\(64\)
Tathmini:\(x^3\) wakati\(x = 6\).
- Jibu
-
\(216\)
Tathmini\(2^x\) wakati\(x = 5\).
Suluhisho
Katika maneno haya, variable ni exponent.
| \(2^{x}\) | |
| Mbadala\(\textcolor{red}{5}\) kwa ajili ya x. | \(2^{\textcolor{red}{5}}\) |
| Tumia ufafanuzi wa exponent. | \(2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\) |
| Kuzidisha | \(32\) |
Wakati\(x = 5\), maneno\(2^x\) ina thamani ya\(32\).
Tathmini:\(2^x\) wakati\(x = 6\).
- Jibu
-
\(64\)
Tathmini:\(3^x\) wakati\(x = 4\).
- Jibu
-
\(81\)
Tathmini\(3x + 4y − 6\) wakati\(x = 10\) na\(y = 2\).
Suluhisho
Maneno haya ina vigezo viwili, hivyo ni lazima kufanya mbadala mbili.
| \(3x + 4y − 6\) | |
| Mbadala\(\textcolor{red}{10}\) ya x na\(\textcolor{blue}{2}\) kwa y. | \(3(\textcolor{red}{10}) + 4(\textcolor{blue}{2}) − 6\) |
| Kuzidisha. | \(30 + 8 - 6\) |
| Ongeza na uondoe kushoto kwenda kulia. | \(32\) |
Wakati\(x = 10\) na\(y = 2\), maneno\(3x + 4y − 6\) ina thamani ya\(32\).
Tathmini:\(2x + 5y − 4\) wakati\(x = 11\) na\(y = 3\)
- Jibu
-
\(33\)
Tathmini:\(5x − 2y − 9\) wakati\(x = 7\) na\(y = 8\)
- Jibu
-
\(10\)
Tathmini\(2x^2 + 3x + 8\) wakati\(x = 4\).
Suluhisho
Tunahitaji kuwa makini wakati kujieleza ina variable na exponent. Katika maneno haya,\(2x^2\) ina maana\(2 • x • x\) na ni tofauti na maneno\((2x)^2\), ambayo ina maana\(2x • 2x\).
| \(2x^{2} + 3x + 8\) | |
| Mbadala\(\textcolor{red}{4}\) kwa kila x. | \(2(\textcolor{red}{4})^{2} + 3(\textcolor{red}{4}) + 8\) |
| Kurahisisha 4 2. | \(2(16) + 3(4) + 8\) |
| Kuzidisha. | \(32 + 12 + 8\) |
| Ongeza. | \(52\) |
Tathmini:\(3x^2 + 4x + 1\) wakati\(x = 3\).
- Jibu
-
\(40\)
Tathmini:\(6x^2 − 4x − 7\) wakati\(x = 2\).
- Jibu
-
\(9\)
Tambua Masharti, Coefficients, na Masharti Kama
Maneno ya algebraic yanajumuishwa na maneno. Neno ni mara kwa mara au bidhaa ya vigezo vya mara kwa mara na moja au zaidi. Baadhi ya mifano ya maneno ni\(7\)\(y\),\(5x^2\),\(9a\), na\(13xy\).
Mara kwa mara ambayo huzidisha variable (s) kwa muda inaitwa mgawo. Tunaweza kufikiria mgawo kama namba mbele ya kutofautiana. Mgawo wa neno\(3x\) ni\(3\). Tunapoandika\(x\), mgawo ni\(1\), tangu\(x = 1 • x\). Jedwali\(\PageIndex{1}\) hutoa coefficients kwa kila maneno katika safu ya kushoto.
| Muda | Mgawo |
|---|---|
| 7 | 7 |
| 9a | 9 |
| y | 1 |
| 5x 2 | 5 |
Maneno ya algebraic yanaweza kuwa na maneno moja au zaidi yaliyoongezwa au yameondolewa. Katika sura hii, tutafanya kazi tu na maneno ambayo yanaongezwa pamoja. Jedwali\(\PageIndex{2}\) linatoa baadhi ya mifano ya maneno ya algebraic na idadi mbalimbali ya maneno. Kumbuka kwamba sisi ni pamoja na operesheni kabla ya muda na hayo.
| Ufafanuzi | Masharti |
|---|---|
| 7 | 7 |
| y | y |
| x 7 | x, 7 |
| 2x 7y + 4 | 2x, 7y, 4 |
| 3x 2 + 4x 2 + 5y + 3 | 3x 2, 4x 2, 5y, 3 |
Tambua kila neno katika maneno\(9b + 15x^2 + a + 6\). Kisha kutambua mgawo wa kila neno.
Suluhisho
Maneno yana maneno manne. Wao ni\(9b\),\(15x^2\),\(a\), na\(6\).
Mgawo wa\(9b\) ni\(9\).
Mgawo wa\(15x^2\) ni\(15\).
Kumbuka kwamba ikiwa hakuna namba iliyoandikwa kabla ya kutofautiana, mgawo ni\(1\). Hivyo mgawo wa ni\(1\).
Mgawo wa mara kwa mara ni mara kwa mara, hivyo mgawo wa\(6\) ni\(6\).
Tambua maneno yote katika maneno yaliyotolewa, na coefficients zao:\(4x + 3b + 2\)
- Jibu
-
Masharti ni\(4x, 3b,\) na\(2\). Coefficients ni\(4, 3,\) na\(2\).
Tambua maneno yote katika maneno yaliyotolewa, na coefficients zao:\(9a + 13a^2 + a^3\)
- Jibu
-
maneno ni\(9a, 13a^2,\) na\(a^3\), coefficients ni\(9, 13,\) na\(1\).
Baadhi ya maneno hushiriki sifa za kawaida. Angalia maneno yafuatayo. Ambayo inaonekana kuwa na sifa za kawaida?
\(5x, 7, n^{2}, 4, 3x, 9n^{2}\)
Ni ipi kati ya maneno haya ni kama maneno?
- Masharti\(7\) na\(4\) ni masharti ya mara kwa mara.
- Masharti\(5x\) na\(3x\) ni masharti yote na\(x\).
- Masharti\(n^2\) na\(9n^2\) wote wawili wana\(n^2\).
Masharti huitwa kama maneno kama wana vigezo sawa na vielelezo. Masharti yote ya mara kwa mara pia yanafanana na maneno. Hivyo kati ya maneno\(5x, 7, n^2, 4, 3x, 9n^2, 7\) na\(4\) ni kama maneno,\(5x\) na\(3x\) ni kama maneno,\(n^2\) na\(9n^2\) ni kama maneno.
Masharti ambayo ni ama constants au kuwa na vigezo sawa na exponents sawa ni kama maneno.
Tambua maneno kama hayo:
- \(y^3, 7x^2, 14, 23, 4y^3, 9x, 5x^2\)
- \(4x^2 + 2x + 5x^2 + 6x + 40x + 8xy\)
Suluhisho
- \(y^3, 7x^2, 14, 23, 4y^3, 9x, 5x^2\)
Angalia vigezo na exponents. Maneno yana\(y^3, x^2, x\), na mara kwa mara. Masharti\(y^3\) na\(4y^3\) ni kama maneno kwa sababu wote wana\(y^3\). Masharti\(7x^2\) na\(5x^2\) ni kama maneno kwa sababu wote wana\(x^2\). Masharti\(14\) na\(23\) ni kama maneno kwa sababu wote wawili ni mara kwa mara. Neno\(9x\) halina maneno kama hayo katika orodha hii kwani hakuna maneno mengine ambayo variable\(x\) kukulia kwa nguvu ya\(1\).
- \(4x^2 + 2x + 5x^2 + 6x + 40x + 8xy\)
Angalia vigezo na exponents. Maneno yana maneno\(4x^2, 2x, 5x^2, 6x, 40x\), na\(8xy\) Masharti\(4x^2\) na\(5x^2\) ni kama maneno kwa sababu wote wana\(x^2\). maneno\(2x, 6x\), na\(40x\) ni kama maneno kwa sababu wote wana\(x\). Neno\(8xy\) halina maneno kama hayo katika usemi uliotolewa kwa sababu hakuna maneno mengine yana vigezo viwili\(xy\).
Tambua maneno kama hayo katika orodha au maneno:\(9, 2x^3, y^2, 8x^3, 15, 9y, 11y^2\)
- Jibu
-
\(9, 15\);\(2x^3\) na\(8x^3\),\(y^2\), na\(11y^2\)
Tambua maneno kama hayo katika orodha au maneno:\(4x^3 + 8x^2 + 19 + 3x^2 + 24 + 6x^3\)
- Jibu
-
\(4x^3\)na\(6x^3\);\(8x^2\) na\(3x^2\);\(19\) na\(24\)
Kurahisisha Maneno kwa Kuchanganya Kama Masharti
Tunaweza kurahisisha kujieleza kwa kuchanganya maneno kama hayo. Unafikiri\(3x + 6x\) ingekuwa kurahisisha kwa? Ikiwa umefikiri\(9x\), ungekuwa sahihi!
Tunaweza kuona kwa nini hii inafanya kazi kwa kuandika maneno yote kama matatizo ya kuongeza.
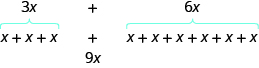
Ongeza coefficients na uendelee kutofautiana sawa. Haijalishi\(x\) ni nini. Ikiwa una\(3\) kitu na kuongeza\(6\) zaidi ya kitu kimoja, matokeo yake ni\(9\) yao. Kwa mfano,\(3\) machungwa pamoja na\(6\) machungwa ni\(9\) machungwa. Tutajadili mali ya hisabati nyuma ya hili baadaye.
Maneno\(3x + 6x\) yana maneno mawili tu. Wakati maneno yana maneno zaidi, inaweza kuwa na manufaa kupanga upya masharti ili maneno kama hayo yameunganishwa. Mali ya Kubadilisha ya Kuongezea inasema kwamba tunaweza kubadilisha utaratibu wa viambatisho bila kubadilisha jumla. Hivyo tunaweza upya kujieleza zifuatazo kabla ya kuchanganya kama maneno.
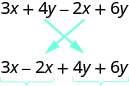
Sasa ni rahisi kuona maneno kama hayo ya kuunganishwa.
Hatua ya 1. Tambua maneno kama hayo.
Hatua ya 2. Panga upya maneno ili kama maneno ni pamoja.
Hatua ya 3. Ongeza coefficients ya maneno kama hayo.
Kurahisisha kujieleza:\(3x + 7 + 4x + 5\).
Suluhisho
| \(3x + 7 + 4x + 5\) | |
| Tambua maneno kama hayo | \(\textcolor{red}{3x} + \textcolor{blue}{7} + \textcolor{red}{4x} + \textcolor{blue}{5}\) |
| Panga upya maneno, hivyo maneno kama hayo ni pamoja. | \(\textcolor{red}{3x} + \textcolor{red}{4x} + \textcolor{blue}{7} + \textcolor{blue}{5}\) |
| Ongeza coefficients ya maneno kama hayo. | \(\textcolor{red}{7x} + \textcolor{blue}{12}\) |
| Maneno ya awali ni rahisi kwa... | \(7x + 12\) |
Kurahisisha:\(7x + 9 + 9x + 8\)
- Jibu
-
\(16x+17\)
Kurahisisha:\(5y + 2 + 8y + 4y + 5\)
- Jibu
-
\(17y+7\)
Kurahisisha kujieleza:\(7x^2 + 8x + x^2 + 4x\).
Suluhisho
| \(7x^{2} + 8x + x^{2} + 4x\) | |
| Tambua maneno kama hayo. | \(\textcolor{red}{7x^{2}} + \textcolor{blue}{8x} + \textcolor{red}{x^{2}} + \textcolor{blue}{4x}\) |
| Panga upya maneno ili kama maneno ni pamoja. | \(\textcolor{red}{7x^{2}} + \textcolor{red}{x^{2}} + \textcolor{blue}{8x} + \textcolor{blue}{4x}\) |
| Ongeza coefficients ya maneno kama hayo. | \(\textcolor{red}{8x^{2}} + \textcolor{blue}{12x}\) |
Haya si kama maneno na haiwezi kuunganishwa. Hivyo\(8x^2 + 12x\) ni katika fomu rahisi.
Kurahisisha:\(3x^2 + 9x + x^2 + 5x\)
- Jibu
-
\(4x^2+14x\)
Kurahisisha:\(11y^2 + 8y + y^2 + 7y\)
- Jibu
-
\(12y^2+15y\)


