1.7: Kuzidisha Idadi nzima (Sehemu ya 1)
- Page ID
- 173368
- Tumia notation ya kuzidisha
- Uzidishaji wa mfano wa idadi nzima
- Kuzidisha idadi nzima
- Tafsiri misemo ya neno kwa nukuu ya hesabu
- Panua idadi nzima katika programu
Kabla ya kuanza, fanya jaribio hili la utayari.
- Ongeza:\(1,683 + 479\). Ikiwa umekosa tatizo hili, kagua Mfano 1.2.10.
- Ondoa:\(605 − 321\). Ikiwa umekosa tatizo hili, kagua Mfano 1.3.4.
Tumia Nukuu ya kuzidisha
Tuseme uliulizwa kuhesabu pennies haya yote inavyoonekana katika Kielelezo\(\PageIndex{1}\).

Kielelezo\(\PageIndex{1}\)
Je, wewe kuhesabu pennies mmoja mmoja? Au je, wewe kuhesabu idadi ya pennies katika kila mstari na kuongeza kwamba\(3\) mara idadi.
\[8 + 8 + 8 \nonumber\]
Kuzidisha ni njia ya kuwakilisha kuongeza mara kwa mara. Hivyo badala ya kuongeza mara\(8\) tatu, tunaweza kuandika kujieleza kuzidisha.
\[3 \times 8 \nonumber \]
Sisi wito kila namba kuwa tele sababu na matokeo ya bidhaa. Tunasoma\(3 × 8\) kama mara tatu nane, na matokeo kama bidhaa ya tatu na nane.
Kuna alama kadhaa zinazowakilisha kuzidisha. Hizi ni pamoja na ishara × pamoja na nukta, •, na mabano ().
Kuelezea kuzidisha, tunaweza kutumia alama na maneno.
| Operesheni | Nukuu | Ufafanuzi | Soma kama | Matokeo |
|---|---|---|---|---|
| Kuzidisha | × | 3 × 8 | mara tatu nane | bidhaa ya 3 na 8 |
| • | 3 • 8 | |||
| () | 3 (8) |
Tafsiri kutoka hesabu nukuu kwa maneno:
- \(7 × 6\)
- \(12 · 14\)
- \(6(13)\)
Suluhisho
- Tunasoma hii kama mara saba sita na matokeo ni bidhaa ya saba na sita.
- Tunasoma hii kama mara kumi na nne na nne na matokeo ni bidhaa ya kumi na mbili na kumi na nne.
- Tunasoma hii kama mara sita kumi na tatu na matokeo ni bidhaa ya sita na kumi na tatu.
Tafsiri kutoka hesabu nukuu kwa maneno:
- \(8 × 7\)
- \(18 • 11\)
- Jibu
-
mara nane saba; bidhaa ya nane na saba
- Jibu b
-
kumi na nane mara kumi na moja; bidhaa ya kumi na nane na kumi na moja
Tafsiri kutoka hesabu nukuu kwa maneno:
- \((13)(7)\)
- \(5(16)\)
- Jibu
-
kumi na tatu mara saba; bidhaa ya kumi na tatu na saba
- Jibu b
-
mara tano kumi na sita; bidhaa ya tano na kumi na sita
Uzidishaji wa mfano wa Hesabu Nzima
Kuna njia nyingi za kuzidisha mfano. Tofauti na sehemu zilizopita ambapo tulitumia\(10\) vitalu vya msingi, hapa tutatumia counters kutusaidia kuelewa maana ya kuzidisha. Counter ni kitu chochote ambacho kinaweza kutumika kwa kuhesabu. Tutatumia counters pande zote za bluu.
Mfano:\(3 × 8\).
Suluhisho
Ili kutengeneza bidhaa\(3 × 8\), tutaanza na safu ya\(8\) counters.

Sababu nyingine ni\(3\), hivyo tutafanya\(3\) safu ya\(8\) counters.

Sasa tunaweza kuhesabu matokeo. Kuna\(24\) counters katika yote.
\[3 \times 8 = 24 \nonumber \]
Kama ukiangalia counters sideways, utaona kwamba tunaweza pia kuwa alifanya\(8\) safu ya\(3\) counters. Bidhaa ingekuwa sawa. Tutaweza kupata nyuma wazo hili baadaye.
Mfano kila kuzidisha:\(4 × 6\).
- Jibu
-

Mfano kila kuzidisha:\(5 × 7\).
- Jibu
-

Kuzidisha Nambari nzima
Ili kuzidisha bila kutumia mifano, unahitaji kujua ukweli wote wa kuzidisha tarakimu moja. Hakikisha unawajua kwa ufasaha kabla ya kuendelea katika sehemu hii. Jedwali\(\PageIndex{2}\) linaonyesha ukweli wa kuzidisha. Kila sanduku inaonyesha bidhaa ya namba chini ya safu ya kushoto na namba katika mstari wa juu. Kama huna uhakika kuhusu bidhaa, mfano ni. Ni muhimu kukariri ukweli wowote wa namba ambazo hujui tayari, hivyo utakuwa tayari kuzidisha idadi kubwa.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Ni nini kinachotokea unapozidisha idadi kwa sifuri? Unaweza kuona kwamba bidhaa ya namba yoyote na sifuri ni sifuri. Hii inaitwa Mali ya Kuzidisha ya Zero.
Bidhaa ya idadi yoyote na\(0\) ni\(0\).
\[a \cdot 0 = 0\]
\[0 \cdot a = 0\]
Kuzidisha:
- \(0 • 11\)
- \((42)0\)
Suluhisho
| Bidhaa ya nambari yoyote na sifuri ni sifuri. | 0 • 11 = 0 |
| Kuongezeka kwa matokeo ya sifuri katika sifuri. | (42) 0 = 0 |
Pata kila bidhaa:
- \(0 • 19\)
- \((39)0\)
- Jibu
-
\(0\)
- Jibu b
-
\(0\)
Pata kila bidhaa:
- \(0 • 24\)
- \((57)0\)
- Jibu
-
\(0\)
- Jibu b
-
\(0\)
Ni nini kinachotokea unapozidisha idadi kwa moja? Kuzidisha idadi kwa moja hakubadilisha thamani yake. Tunaita ukweli huu Mali ya Utambulisho wa Kuzidisha, na\(1\) inaitwa utambulisho wa kuzidisha.
Bidhaa ya nambari yoyote na\(1\) ni namba.
\[1 \cdot a = a\]
\[a \cdot 1 = a\]
Kuzidisha:
- \((11)1\)
- \(1 • 42\)
Suluhisho
| Bidhaa ya namba yoyote na moja ni namba. | (11) 1 = 11 |
| Kuongezeka kwa moja hakubadilisha thamani. | 1 • 42 = 42 |
Pata kila bidhaa:
- \((19)1\)
- \(1 • 39\)
- Jibu
-
\(19\)
- Jibu b
-
\(39\)
Pata kila bidhaa:
- \((24)(1)\)
- \(1 × 57\)
- Jibu
-
\(24\)
- Jibu b
-
\(57\)
Mapema katika sura hii, tulijifunza kwamba Mali ya Kubadilisha ya Aidha inasema kuwa kubadilisha utaratibu wa kuongeza haubadili jumla. Tuliona kwamba\(8 + 9 = 17\) ni sawa na\(9 + 8 = 17\).
Je, hii pia ni kweli kwa kuzidisha? Hebu tuangalie jozi chache za mambo.
\[\begin{split} 4 \cdot 7 & = 28 \qquad 7 \cdot 4 = 28 \\ 9 \cdot 7 & = 63 \qquad 7 \cdot 9 = 63 \\ 8 \cdot 9 & = 72 \qquad 9 \cdot 8 = 72 \end{split}\]
Wakati utaratibu wa mambo umebadilishwa, bidhaa haibadilika. Hii inaitwa Mali ya Commutative ya Kuzidisha.
Kubadilisha utaratibu wa mambo haubadili bidhaa zao.
\[a \cdot b = b \cdot a\]
Kuzidisha:
- \(8 • 7\)
- \(7 • 8\)
Suluhisho
| Kuzidisha. | 8 • 7 = 56 |
| Kuzidisha. | 7 • 8 = 56 |
Kubadilisha utaratibu wa mambo haubadili bidhaa.
Kuzidisha:
- \(9 • 6\)
- \(6 • 9\)
- Jibu
-
\(54\)
- Jibu b
-
\(54\)
Kuzidisha:
- \(8 • 6\)
- \(6 • 8\)
- Jibu
-
\(48\)
- Jibu b
-
\(48\)
Ili kuzidisha idadi na tarakimu zaidi ya moja, kwa kawaida ni rahisi kuandika namba kwa wima katika nguzo kama tulivyofanya kwa kuongeza na kuondoa.

Tunaanza kwa kuzidisha\(3\) na\(7\).
\[3 \times 7 = 21 \nonumber \]
Tunaandika\(1\) katika sehemu moja ya bidhaa. Tunachukua\(2\) makumi kwa kuandika\(2\) juu ya mahali pa makumi.

Kisha sisi kuzidisha\(3\) kwa\(2\), na kuongeza\(2\) juu ya makumi mahali kwa bidhaa. Hivyo\(3 × 2 = 6\), na\(6 + 2 = 8\). Andika\(8\) katika sehemu ya makumi ya bidhaa.

Bidhaa ni\(81\).
Tunapozidisha namba mbili na idadi tofauti ya tarakimu, kwa kawaida ni rahisi kuandika idadi ndogo chini. Unaweza kuandika kwa njia nyingine, pia, lakini njia hii ni rahisi kufanya kazi na.
Kuzidisha:\(15 • 4\).
Suluhisho
| Andika namba ili tarakimu 5 na 4 zinasimama kwa wima. |  |
| Panua 4 kwa tarakimu katika sehemu moja ya 15. 4 • 5 = 20. | |
| Andika 0 katika sehemu moja ya bidhaa na kubeba makumi 2. |  |
| Panua 4 kwa tarakimu katika mahali pa makumi ya 15. 4 - 1 = 4. Ongeza makumi 2 tuliyobeba. 4 + 2 = 6. | |
| Andika 6 katika sehemu ya makumi ya bidhaa. |  |
Kuzidisha:\(64 • 8\).
- Jibu
-
\(512\)
Kuzidisha:\(57 • 6\).
- Jibu
-
\(342\)
Kuzidisha:\(286 • 5\).
Suluhisho
| Andika namba ili tarakimu 5 na 6 ziweke kwenye wima. | 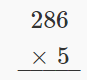 |
| Panua 5 kwa tarakimu katika sehemu moja ya 286. 5 • 6 = 30. | |
| Andika 0 katika sehemu moja ya bidhaa na kubeba 3 hadi mahali pa makumi. Panua 5 kwa tarakimu katika mahali pa makumi ya 286. 5 • 8 = 40. | 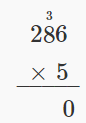 |
| Ongeza makumi 3 tuliyobeba ili kupata 40 + 3 = 43. Andika 3 katika sehemu ya makumi ya bidhaa na kubeba 4 hadi mahali pa mamia. |  |
| Kuzidisha 5 kwa tarakimu katika sehemu ya mamia ya 286. 5 • 2 = 10. Ongeza mamia ya 4 tuliyobeba ili kupata 10 + 4 = 14. Andika 4 katika sehemu ya mamia ya bidhaa na 1 kwa maelfu mahali. |  |
Kuzidisha:\(347 • 5\).
- Jibu
-
\(1,735\)
Kuzidisha:\(462 • 7\).
- Jibu
-
\(3,234\)
Tunapozidisha kwa namba na tarakimu mbili au zaidi, tunazidisha kwa kila tarakimu tofauti, kufanya kazi kutoka kulia kwenda kushoto. Kila bidhaa tofauti ya tarakimu inaitwa bidhaa ya sehemu. Tunapoandika bidhaa za sehemu, lazima tuhakikishe kuzingatia maadili ya mahali.
Hatua ya 1. Andika namba ili kila thamani mahali mistari up wima.
Hatua ya 2. Panua tarakimu katika kila thamani ya mahali.
- Kazi kutoka kulia kwenda kushoto, kuanzia na mahali pekee kwenye nambari ya chini.
- Panua nambari ya chini kwa tarakimu moja kwenye nambari ya juu, kisha kwa tarakimu kumi, na kadhalika.
- Ikiwa bidhaa katika thamani ya mahali ni zaidi ya 9, kubeba thamani ya mahali inayofuata.
- Andika bidhaa za sehemu, ukiweka tarakimu katika maadili ya mahali na namba zilizo hapo juu.
- Kurudia kwa makumi mahali katika idadi ya chini, mahali mamia, na kadhalika.
- Weka sifuri kama kishika na kila bidhaa ya ziada ya sehemu.
Hatua ya 3. Ongeza bidhaa za sehemu.
Kuzidisha:\(62(87)\).
Suluhisho
| Andika namba ili kila mahali mistari up vertically | 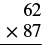 |
| Anza kwa kuzidisha 7 na 62. Panua 7 kwa tarakimu katika sehemu moja ya 62. 7 • 2 = 14. Andika 4 katika sehemu moja ya bidhaa na kubeba 1 hadi mahali pa makumi. |  |
| Panua 7 kwa tarakimu katika mahali pa makumi ya 62. 7 • 6 = 42. Ongeza kumi ya 1 tuliyobeba. 42 + 1 = 43. Andika 3 katika sehemu ya makumi ya bidhaa na 4 katika mahali pa mamia. | 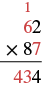 |
| Bidhaa ya kwanza ya sehemu ni 434. | |
| Sasa, andika 0 chini ya 4 katika sehemu moja ya bidhaa inayofuata ya sehemu kama kishika tangu sasa tunazidisha tarakimu katika mahali pa makumi ya 87 na 62. Panua 8 kwa tarakimu katika sehemu moja ya 62. 8 • 2 = 16. Andika 6 katika sehemu inayofuata ya bidhaa, ambayo ni mahali pa makumi. Weka 1 hadi mahali pa makumi. |  |
| Kuzidisha 8 na 6, tarakimu katika mahali pa makumi ya 62, kisha kuongeza 1 kumi tuliyobeba ili kupata 49. Andika 9 katika sehemu ya mamia ya bidhaa na 4 katika maelfu mahali. |  |
| Bidhaa ya pili ya sehemu ni 4960. Ongeza bidhaa za sehemu. |  |
Bidhaa ni\(5,394\).
Kuzidisha:\(43(78)\).
- Jibu
-
\(3,354\)
Kuzidisha:\(64(59)\).
- Jibu
-
\(3,776\)
Kuzidisha:
- \(47 • 10\)
- \(47 • 100\)
Suluhisho
| (a) 47 • 10 |  |
| (b) 47 • 100 |  |
Wakati sisi kuzidisha\(47\) mara\(10\), bidhaa ilikuwa\(470\). Taarifa kwamba\(10\) ina sifuri moja, na sisi kuweka sifuri moja baada ya\(47\) kupata bidhaa. Wakati sisi kuzidisha\(47\) mara\(100\), bidhaa ilikuwa\(4,700\). Taarifa kwamba\(100\) ina zero mbili na sisi kuweka zeros mbili baada ya\(47\) kupata bidhaa.
Je! Unaona mfano? Kama sisi kuzidisha\(47\) mara\(10,000\), ambayo ina zeros nne, tutakuwa kuweka zeros nne baada ya\(47\) kupata bidhaa\(470,000\).
Kuzidisha:
- \(54 • 10\)
- \(54 • 100\)
- Jibu
-
\(540\)
- Jibu b
-
\(5,400\)
Kuzidisha:
- \(75 • 10\)
- \(75 • 100\)
- Jibu
-
\(750\)
- Jibu
-
\(7,500\)
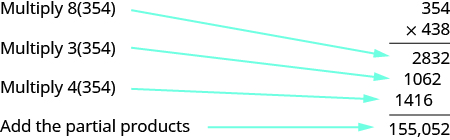
Kuzidisha:\(354(438)\).
Suluhisho
Kuna tarakimu tatu katika mambo hivyo kutakuwa na bidhaa za\(3\) sehemu. Hatuna kuandika\(0\) kama kishika kwa muda mrefu kama sisi kuandika kila bidhaa sehemu katika mahali sahihi.
Kuzidisha:\(265(483)\).
- Jibu
-
\(127,995\)
Kuzidisha:\(823(794)\).
- Jibu
-
\(653,462\)
Kuzidisha:\(896(201)\).
Suluhisho
Kuna lazima iwe na bidhaa za\(3\) sehemu. Bidhaa ya pili ya sehemu itakuwa matokeo ya kuzidisha\(896\) na\(0\).
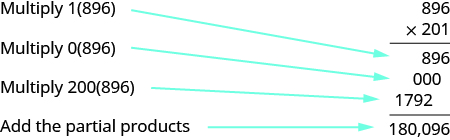
Angalia kwamba bidhaa ya pili ya sehemu ya zero zote haiathiri matokeo. Tunaweza mahali sifuri kama kishika katika mahali mamia na kisha kuendelea moja kwa moja na kuzidisha kwa\(2\) katika mamia mahali, kama inavyoonekana.
Kuzidisha kwa\(10\), lakini ingiza sifuri moja tu kama kishika mahali pa makumi. Kuzidisha kwa\(200\), kuweka\(2\) kutoka\(12\). \(2 • 6 = 12\)katika mahali mamia.

Kuzidisha:\((718)509\).
- Jibu
-
\(365,462\)
Kuzidisha:\((627)804\).
- Jibu
-
\(504,108\)
Wakati kuna mambo matatu au zaidi, tunazidisha mbili za kwanza na kisha kuzidisha bidhaa zao kwa sababu inayofuata. Kwa mfano:
| kuzidisha | 8 • 3 • 2 |
| kwanza kuzidisha 8 • 3 | 24 • 2 |
| kisha kuzidisha 24 • 2 | 48 |


