1.3: Ongeza Hesabu nzima (Sehemu ya 1)
- Page ID
- 173371
- Tumia maelezo ya kuongeza
- Kuongezea mfano wa idadi nzima
- Ongeza namba nzima bila mifano
- Tafsiri misemo ya neno kwa nukuu ya hesabu
- Ongeza namba nzima katika programu
Kabla ya kuanza, fanya jaribio hili la utayari.
- Nambari inayotokana na\(10\) vitalu vya msingi ni nini? Ikiwa umekosa tatizo hili, kagua Mfano 1.1.2.

Kielelezo\(\PageIndex{1}\)
- Andika namba mia tatu arobaini na mbili elfu sita kwa kutumia tarakimu? Ikiwa umekosa tatizo hili, kagua Mfano 1.1.6.
Tumia Nukuu ya kuongeza
Mwanafunzi wa chuo ana kazi ya wakati mmoja. Wiki iliyopita alifanya kazi\(3\) masaa Jumatatu na\(4\) masaa Ijumaa. Kupata jumla ya idadi ya masaa alifanya kazi wiki iliyopita, aliongeza\(3\) na\(4\).
Uendeshaji wa kuongeza unachanganya namba ili kupata jumla. Nukuu tunayotumia ili kupata jumla ya\(3\) na\(4\) ni:
\[3 + 4 \nonumber \]
Tunasoma hii kama tatu pamoja na nne na matokeo ni jumla ya tatu na nne. Nambari\(3\) na\(4\) huitwa viambatisho. Taarifa ya hesabu ambayo inajumuisha namba na shughuli inaitwa kujieleza.
Kuelezea kuongeza, tunaweza kutumia alama na maneno.
| Operesheni | Nukuu | Ufafanuzi | Soma kama | Matokeo |
|---|---|---|---|---|
| Ongezeko | + | 3+4 | tatu pamoja na nne | jumla ya 3 na 4 |
Tafsiri kutoka hesabu nukuu kwa maneno:
- \(7 + 1\)
- \(12 + 14\)
Suluhisho
- Maneno haya yana alama ya pamoja inayounganisha viambatisho\(7\) na\(1\). Tunasoma hii kama saba pamoja na moja. Matokeo ni jumla ya saba na moja.
- Maneno haya yana alama ya pamoja inayounganisha viambatisho\(12\) na\(14\). Tunasoma hii kama kumi na mbili pamoja na kumi na nne. Matokeo yake ni jumla ya kumi na mbili na kumi na nne.
Tafsiri kutoka hesabu nukuu kwa maneno:
- \(8 + 4\)
- \(18 + 11\)
- Jibu
-
nane pamoja na nne; jumla ya nane na nne
- Jibu b
-
kumi na nane na kumi na moja; jumla ya kumi na nane na kumi na moja
Tafsiri kutoka hesabu nukuu kwa maneno:
- \(21 + 16\)
- \(100 + 200\)
- Jibu
-
ishirini na moja pamoja na kumi na sita; jumla ya ishirini na moja na kumi na sita
- Jibu b
-
mia moja pamoja na mia mbili; jumla ya mia moja na mia mbili
Uongeze wa mfano wa Hesabu Nzima
Aidha ni kweli tu kuhesabu. Tutaongeza mfano na\(10\) vitalu vya msingi. Kumbuka, block inawakilisha\(1\) na fimbo inawakilisha\(10\). Hebu tuanze kwa kuimarisha maelezo ya kuongeza tuliyozingatia tu,\(3 + 4\).
Kila addend ni chini ya 10, hivyo tunaweza kutumia wale vitalu.
|
Tunaanza kwa kuimarisha namba ya kwanza na vitalu 3. |
 |
|
Kisha sisi mfano namba ya pili na vitalu 4. |
 |
|
Hesabu idadi ya vitalu. |
 |
Kuna\(7\) vitalu katika yote. Tunatumia ishara sawa (\(=\)) ili kuonyesha jumla. Sentensi ya hesabu inayoonyesha kwamba maneno mawili ni sawa inaitwa equation. Tumeonyesha kuwa\(3 + 4 = 7\).
Mfano wa kuongeza\(2 + 6\).
Suluhisho
\(2 + 6\)ina maana jumla ya\(2\) na\(6\)
Kila addend ni chini ya\(10\), hivyo tunaweza kutumia wale vitalu.
| Tengeneza nambari ya kwanza na vitalu 2. |  |
| Tengeneza nambari ya pili na vitalu 6. |  |
| Hesabu idadi ya vitalu |  |
| Kuna vitalu 8 kwa wote, hivyo 2 + 6 = 8. |
Mfano:\(3 + 6\).
- Jibu
-
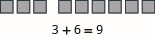
Mfano:\(5 + 1\).
- Jibu
-
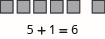
Wakati matokeo ni\(10\) au zaidi ya vitalu, tutabadilisha\(10\) vitalu kwa fimbo moja.
Mfano wa kuongeza\(5 + 8\).
Suluhisho
\(5 + 8\)ina maana jumla ya\(5\) na\(8\).
| Kila nyongeza ni chini ya 10, se tunaweza kutumia wale vitalu. | |
| Tengeneza nambari ya kwanza na vitalu 5. |  |
| Tengeneza nambari ya pili na vitalu 8. |  |
| Hesabu matokeo. Kuna vitalu zaidi ya 10 hivyo tunabadilishana 10 vitalu kwa fimbo ya makumi 1. | 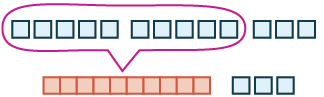 |
| Sasa tuna 1 kumi na 3, ambayo ni 13. | $5 + 8 = 13 $$ |
Angalia kwamba tunaweza kuelezea mifano kama wale vitalu na fimbo kumi, au tunaweza tu kusema wale na makumi. Kuanzia sasa, tutatumia toleo fupi lakini kukumbuka kwamba wanamaanisha kitu kimoja.
Mfano wa kuongeza:\(5 + 7\)
- Jibu
-
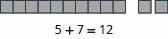
Mfano wa kuongeza:\(6 + 8\).
- Jibu
-
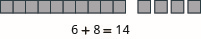
Mfano wa kuongeza:\(17 + 26\).
Suluhisho
\(17 + 26\)ina maana jumla ya\(17\) na\(26\).
| mfano 17. | 1 kumi na 7 |  |
| mfano 26. | 2 makumi na 6 |  |
| Kuchanganya. | 3 makumi na 13 |  |
| Exchange 10 kwa 1 kumi. |
4 makumi na 3 40 + 3 = 43 |
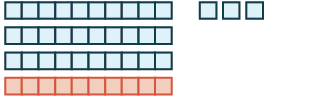 |
| Tumeonyesha kuwa 17 + 26 = 43 |
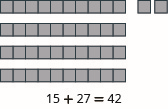
Mfano kila kuongeza:\(15 + 27\).
- Jibu
-
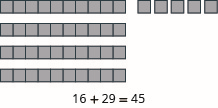
Mfano kila kuongeza:\(16 + 29\).
- Jibu
-
Ongeza Hesabu Nzima bila Mifano
Sasa kwa kuwa tumetumia mifano ya kuongeza namba, tunaweza kuendelea na kuongeza bila mifano. Kabla ya kufanya hivyo, hakikisha unajua ukweli wote wa tarakimu moja. Utahitaji kutumia ukweli huu wa nambari unapoongeza idadi kubwa.
Fikiria kujaza Jedwali\(\PageIndex{1}\) kwa kuongeza kila nambari ya mstari upande wa kushoto kwa kila nambari ya safu juu. Hakikisha kwamba unapata kila jumla iliyoonyeshwa. Ikiwa una shida, fanya mfano. Ni muhimu kwamba wewe kukariri idadi yoyote ukweli huna tayari kujua ili uweze haraka na kwa uhakika kutumia ukweli idadi wakati wewe kuongeza idadi kubwa.
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Je, umeona nini kinatokea unapoongeza sifuri kwa nambari? Jumla ya idadi yoyote na sifuri ni namba yenyewe. Tunaita hii Mali Identity ya Aidha. Zero inaitwa utambulisho wa kuongezea.
Jumla ya idadi yoyote\(a\) na\(0\) ni idadi.
\[a + 0 = a\]
\[0 + a = a\]
Pata kila jumla:
- \(0 + 11\)
- \(42 + 0\)
Suluhisho
|
0 + 11 = 11 |
|
42 + 0 = 42 |
Pata kila jumla:
- \(0 + 19\)
- \(39 + 0\)
- Jibu
-
\(0+19=19\)
- Jibu b
-
\(39+0=39\)
Pata kila jumla:
- \(0 + 24\)
- \(57 + 0\)
- Jibu
-
\(0+24=24\)
- Jibu b
-
\(57+0=57\)
Angalia jozi ya kiasi.
| 2 + 3 = 5 | 3 + 2 = 5 |
| 4 + 7 = 11 | 7 + 4 = 11 |
| 8 + 9 = 17 | 9 + 8 = 17 |
Angalia kwamba wakati utaratibu wa viambatisho unapobadilishwa, jumla haibadilika. Mali hii inaitwa Mali ya Kubadilisha ya Kuongeza, ambayo inasema kuwa kubadilisha utaratibu wa viambatisho havibadili jumla yao.
Kubadilisha utaratibu wa viambatisho a na b havibadili jumla yao.
\[a + b = b + a\]
Ongeza:
- \(8 + 7\)
- \(7 + 8\)
Suluhisho
- \(\begin{align*} 8+7 & \\ 15 & \end{align*}\)
- \(\begin{align*} 7 + 8 & \\ 15 & \end{align*}\)
Kuongeza:\(9 + 7\) na\(7 + 9\).
- Jibu
-
\(9+7=16; 7+9=16\)
Kuongeza:\(8 + 6\) na\(6 + 8\).
- Jibu
-
\(8+6=14; 6+8=14\)
Ongeza:\(28 + 61\).
Suluhisho
Ili kuongeza namba na tarakimu zaidi ya moja, mara nyingi ni rahisi kuandika namba kwa wima kwenye nguzo.
| Andika nambari ili wale na tarakimu kumi ziweke kwenye wima. | 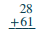 |
| Kisha kuongeza tarakimu katika kila thamani ya mahali. Ongeza wale: 8 + 1 = 9. | 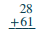 |
| Ongeza makumi: 2 + 6 = 8. | 89 |
Ongeza:\(32 + 54\).
- Jibu
-
\(32+54=86\)
Ongeza:\(25 + 74\).
- Jibu
-
\(25+74=99\)
Katika mfano uliopita, jumla ya wale na jumla ya makumi walikuwa chini ya\(10\). Lakini ni nini kinachotokea ikiwa jumla ni\(10\) au zaidi? Hebu tutumie msingi wetu\(10\) wa mfano ili kujua. Kielelezo\(\PageIndex{2}\) inaonyesha kuongeza ya\(17\) na\(26\) tena.
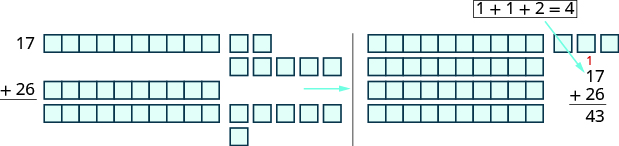
Kielelezo\(\PageIndex{2}\)
Wakati sisi kuongeza ndio\(7 + 6\), sisi kupata\(13\) ndio. Kwa sababu tuna zaidi ya\(10\) wale, tunaweza kubadilishana\(10\) wale kwa\(1\) kumi. Sasa tuna\(4\) makumi na\(3\) wale. Bila kutumia mfano, tunaonyesha hii kama nyekundu ndogo\(1\) juu ya tarakimu katika mahali pa makumi.
Wakati jumla katika safu ya thamani ya mahali ni kubwa kuliko\(9\), tunaendelea kwenye safu inayofuata upande wa kushoto. Kubeba ni sawa na kuunganisha kwa kubadilishana. Kwa mfano,\(10\) ndio kwa\(1\) kumi au\(10\) makumi kwa\(1\) mia.
Hatua ya 1. Andika namba ili kila thamani mahali mistari up wima.
Hatua ya 2. Ongeza tarakimu katika kila thamani ya mahali. Kazi kutoka kulia kwenda kushoto kuanzia na mahali pekee. Ikiwa jumla katika thamani ya mahali ni zaidi ya\(9\), kubeba kwa thamani ya mahali inayofuata.
Hatua ya 3. Endelea kuongeza thamani ya kila mahali kutoka kulia kwenda kushoto, uongeze thamani ya kila mahali na kubeba ikiwa inahitajika.
Ongeza:\(43 + 69\).
Suluhisho
| Andika namba ili tarakimu ziweke kwenye wima. | 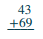 |
| Ongeza tarakimu kila mahali. Ongeza wale: 3 + 9 = 12. | |
| Andika 2 katika sehemu moja kwa jumla. Ongeza 1 kumi hadi mahali pa makumi. | 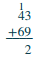.png) |
| Sasa ongeza makumi: 1 + 4 + 6 = 11. Andika 11 kwa jumla. | 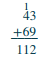.png) |
Ongeza:\(35 + 98\).
- Jibu
-
\(35+98=133\)
Ongeza:\(72 + 89\).
- Jibu
-
\(72+89=161\)
Ongeza:\(324 + 586\).
Suluhisho
| Andika namba ili tarakimu ziweke kwenye wima. | 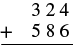 |
| Ongeza tarakimu katika kila thamani ya mahali. Ongeza wale: 4 + 6 = 10. Andika 0 katika sehemu moja kwa jumla na kubeba 1 kumi hadi mahali pa makumi. | 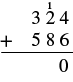 |
| Ongeza makumi: 1 + 2 + 8 = 11. Andika 1 katika mahali pa makumi kwa jumla na kubeba mia 1 hadi mamia. | 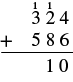 |
| Ongeza mamia: 1 + 3 + 5 = 9. Andika 9 katika mahali mamia. | 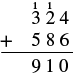 |
Ongeza:\(456 + 376\).
- Jibu
-
\(456+376=832\)
Ongeza:\(269 + 578\).
- Jibu
-
\(269+578=847\)
Ongeza:\(1,683 + 479\).
Suluhisho
| Andika namba ili tarakimu ziweke kwenye wima. | 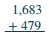.png) |
| Ongeza tarakimu katika kila thamani ya mahali | |
| Ongeza wale: 3 + 9 = 12. Andika 2 katika sehemu moja ya jumla na kubeba 1 kumi hadi mahali pa makumi. | 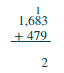.png) |
| Ongeza makumi: 1 + 7 + 8 = 16. Andika 6 katika mahali pa makumi na kubeba mia 1 hadi mahali pa mamia. | 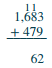.png) |
| Ongeza mamia: 1 + 6 + 4 = 11. Andika 1 katika mahali mamia na kubeba 1 elfu mahali maelfu | 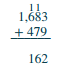.png) |
| Ongeza maelfu 1 + 1 = 2. Andika 2 katika sehemu ya maelfu ya jumla. | .png) |
Wakati viambatisho vina namba tofauti za tarakimu, kuwa makini kuzingatia maadili ya mahali yanayofanana kuanzia na wale na kusonga upande wa kushoto.
Ongeza:\(4,597 + 685\).
- Jibu
-
\(4,597+685=5,282\)
Ongeza:\(5,837 + 695\).
- Jibu
-
\(5,837+695=6,532\)
Ongeza:\(21,357 + 861 + 8,596\).
Suluhisho
| Andika namba ili maadili ya mahali yanapanda wima. | .png) |
| Ongeza tarakimu katika kila thamani ya mahali. | |
| Ongeza wale: 7 + 1 + 6 = 14. Andika 4 katika sehemu moja ya jumla na kubeba 1 hadi mahali pa makumi. | .png) |
| Ongeza makumi: 1 + 5 + 6 + 9 = 21. Andika 1 katika mahali pa makumi na kubeba 2 hadi mahali pa mamia. | .png) |
| Ongeza mamia: 2 + 3 + 8 + 5 = 18. Andika 8 katika mahali mamia na kubeba 1 kwa mahali maelfu. | .png) |
| Ongeza maelfu 1 + 1 + 8 = 10. Andika 0 katika mahali maelfu na kubeba 1 hadi mahali maelfu kumi. | .png) |
| Ongeza maelfu kumi 1 + 2 = 3. Andika 3 katika maelfu kumi mahali kwa jumla. | 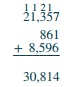.png) |
Mfano huu ulikuwa na viambatisho vitatu. Tunaweza kuongeza idadi yoyote ya viambatisho kwa kutumia mchakato huo kwa muda mrefu kama sisi ni makini kwa line up maadili mahali kwa usahihi.
Ongeza:\(46,195 + 397 + 6,281\).
- Jibu
-
\(46,195 + 397 + 6,281=52,873\)
Ongeza:\(53,762 + 196 + 7,458\).
- Jibu
-
\(53,762 + 196 + 7,458=61,416\)


