Sura ya 9 Mazoezi Mapitio
- Page ID
- 177323
Sura ya 9 Mazoezi Mapitio
Kurahisisha na Tumia mizizi ya Mraba
Punguza Maneno na Mizizi ya Mraba
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{64}\)
\(\sqrt{144}\)
- Jibu
-
12
\(−\sqrt{25}\)
\(−\sqrt{81}\)
- Jibu
-
—9
\(\sqrt{−9}\)
\(\sqrt{−36}\)
- Jibu
-
si idadi halisi
\(\sqrt{64}+\sqrt{225}\)
\(\sqrt{64+225}\)
- Jibu
-
17
Katika mazoezi yafuatayo, tathmini kila mizizi ya mraba kati ya namba mbili za mfululizo.
\(\sqrt{28}\)
\(\sqrt{155}\)
- Jibu
-
\(12<\sqrt{155}<13\)
Mizizi ya Mraba
Katika mazoezi yafuatayo, takriban kila mizizi ya mraba na pande zote kwa maeneo mawili ya decimal.
\(\sqrt{15}\)
\(\sqrt{57}\)
- Jibu
-
7.55
Punguza maneno ya kutofautiana na Mizizi ya Mraba
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{q^2}\)
\(\sqrt{64b^2}\)
- Jibu
-
8b
\(−\sqrt{121a^2}\)
\(\sqrt{225m^{2}n^{2}}\)
- Jibu
-
15mn
\(−\sqrt{100q^2}\)
\(\sqrt{49y^2}\)
- Jibu
-
7y
\(\sqrt{4a^{2}b^{2}}\)
\(\sqrt{121c^{2}d^{2}}\)
- Jibu
-
11cd
Kurahisisha mizizi ya mraba
Tumia mali ya Bidhaa ili kurahisisha Mizizi ya Mraba
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{300}\)
\(\sqrt{98}\)
- Jibu
-
\(7\sqrt{2}\)
\(\sqrt{x^{13}}\)
\(\sqrt{y^{19}}\)
- Jibu
-
\(y^{9}\sqrt{y}\)
\(\sqrt{16m^4}\)
\(\sqrt{36n^{13}}\)
- Jibu
-
\(6n^{6}\sqrt{n}\)
\(\sqrt{288m^{21}}\)
\(\sqrt{150n^7}\)
- Jibu
-
\(5n^3\sqrt{6n}\)
\(\sqrt{48r^{5}s^{4}}\)
\(\sqrt{108r^{5}s^{3}}\)
- Jibu
-
\(6r^{2}s\sqrt{3rs}\)
\(\frac{10−\sqrt{50}}{5}\)
\(\frac{6+\sqrt{72}}{6}\)
- Jibu
-
\(1+\sqrt{2}\)
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{\frac{16}{25}}\)
\(\sqrt{\frac{81}{36}}\)
- Jibu
-
\(\frac{3}{2}\)
\(\sqrt{\frac{x^8}{x^4}}\)
\(\sqrt{\frac{y^6}{y^2}}\)
- Jibu
-
\(y^2\)
\(\sqrt{\frac{98p^6}{2p^2}}\)
\(\sqrt{\frac{72q^8}{2q^4}}\)
- Jibu
-
\(6q^2\)
\(\sqrt{\frac{65}{121}}\)
\(\sqrt{\frac{26}{169}}\)
- Jibu
-
\(\frac{\sqrt{26}}{13}\)
\(\sqrt{\frac{64x^4}{25x^2}}\)
\(\sqrt{\frac{36r^{10}}{16r^5}}\)
- Jibu
-
\(\frac{3r^2\sqrt{r}}{2}\)
\(\sqrt{\frac{48p^{3}q^{5}}{27pq}}\)
\(\sqrt{\frac{12r^{5}s^{7}}{75r^{2}s}}\)
- Jibu
-
\(\frac{2rs^3\sqrt{r}}{5}\)
Ongeza na Ondoa Mizizi ya Mraba
Ongeza na Ondoa Kama Mizizi ya Mraba
Katika mazoezi yafuatayo, kurahisisha.
\(3\sqrt{2}+\sqrt{2}\)
\(5\sqrt{5}+7\sqrt{5}\)
- Jibu
-
\(12\sqrt{5}\)
\(4\sqrt{y}+4\sqrt{y}\)
\(6\sqrt{m}−2\sqrt{m}\)
- Jibu
-
\(4\sqrt{m}\)
\(−3\sqrt{7}+2\sqrt{7}−\sqrt{7}\)
\(8\sqrt{13}+2\sqrt{3}+3\sqrt{13}\)
- Jibu
-
\(11\sqrt{13}+2\sqrt{3}\)
\(3\sqrt{5xy}−\sqrt{5xy}+3\sqrt{5xy}\)
\(2\sqrt{3rs}+\sqrt{3rs}−5\sqrt{rs}\)
- Jibu
-
\(3\sqrt{3rs}−5\sqrt{rs}\)
Ongeza na Ondoa Mizizi ya Mraba ambayo inahitaji kurahisisha
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{32}+3\sqrt{2}\)
\(\sqrt{8}+\sqrt{32}\)
- Jibu
-
\(5\sqrt{2}\)
\(\sqrt{72}+\sqrt{50}\)
\(\sqrt{48}+\sqrt{75}\)
- Jibu
-
\(9\sqrt{3}\)
\(3\sqrt{32}+\sqrt{98}\)
\(\frac{1}{3}\sqrt{27}−\frac{1}{8}\sqrt{192}\)
- Jibu
-
0
\(\sqrt{50y^5}−\sqrt{72y^5}\)
Kuongeza mazoezi Nakala hapa.
- Jibu
-
\(17n^2\sqrt{2}\)
Kuzidisha mizizi ya Mraba
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{2}·\sqrt{20}\)
\(2\sqrt{2}·6\sqrt{14}\)
- Jibu
-
\(24\sqrt{7}\)
\(\sqrt{2m^2}·\sqrt{20m^4}\)
\((\sqrt{62y})(\sqrt{350y^3})\)
- Jibu
-
\(180y^2\)
\((6\sqrt{3v^4})(5\sqrt{30v})\)
\((\sqrt{8})^2\)
- Jibu
-
8
\((−\sqrt{10})^2\)
\((2\sqrt{5})(5\sqrt{5})\)
- Jibu
-
50
\((−3\sqrt{3})(5\sqrt{18})\)
Katika mazoezi yafuatayo, kurahisisha.
\(10(2−\sqrt{7})\)
- Jibu
-
\(20−10\sqrt{7}\)
\(\sqrt{3}(4+\sqrt{12})\)
\((5+\sqrt{2})(3−\sqrt{2})\)
- Jibu
-
\(13−2\sqrt{2}\)
\((5−3\sqrt{7})(1−2\sqrt{7})\)
\((1−3\sqrt{x})(5+2\sqrt{x})\)
- Jibu
-
\(5−13\sqrt{x}−6x\)
\((3+4\sqrt{y})(10−\sqrt{y})\)
\((1+6\sqrt{p})^2\)
- Jibu
-
\(1+12\sqrt{p}+36p\)
\((2−6\sqrt{5})^2\)
\((3+2\sqrt{7})(3−2\sqrt{7})\)
- Jibu
-
19-19
\((6−\sqrt{11})(6+\sqrt{11})\)
Gawanya mizizi ya mraba
Gawanya mizizi ya mraba
Katika mazoezi yafuatayo, kurahisisha.
\(\frac{\sqrt{75}}{10}\)
- Jibu
-
\(\frac{\sqrt{3}}{2}\)
\(\frac{2−\sqrt{12}}{6}\)
\(\frac{\sqrt{48}}{\sqrt{27}}\)
- Jibu
-
\(\frac{4}{3}\)
\(\frac{\sqrt{75x^7}}{\sqrt{3x^3}}\)
\(\frac{\sqrt{20y^5}}{\sqrt{2y}}\)
- Jibu
-
\(y^2\sqrt{10}\)
\(\frac{\sqrt{98p^{6}q^{4}}}{\sqrt{2p^{4}q^{8}}}\)
Katika mazoezi yafuatayo, rationalize denominator.
\(\frac{10}{\sqrt{15}}\)
- Jibu
-
\(\frac{2\sqrt{15}}{3}\)
\(\frac{6}{\sqrt{6}}\)
\(\frac{5}{3\sqrt{5}}\)
- Jibu
-
\(\frac{\sqrt{5}}{3}\)
\(\frac{10}{2\sqrt{6}}\)
\(\sqrt{\frac{3}{28}}\)
- Jibu
-
\(\frac{\sqrt{21}}{14}\)
\(\sqrt{\frac{9}{75}}\)
Katika mazoezi yafuatayo, rationalize denominator.
\(\frac{4}{4+\sqrt{27}}\)
- Jibu
-
\(\frac{16−12\sqrt{3}}{−11}\)
\(\frac{5}{2−\sqrt{10}}\)
\(\frac{4}{2−\sqrt{5}}\)
- Jibu
-
\(−8−4\sqrt{5}\)
\(\frac{5}{4−\sqrt{8}}\)
\(\frac{\sqrt{2}}{\sqrt{p}+\sqrt{3}}\)
- Jibu
-
\(\frac{\sqrt{2p}−\sqrt{6}}{p−3}\)
\(\frac{\sqrt{x}−\sqrt{2}}{\sqrt{x}+\sqrt{2}}\)
Tatua Equations na Mizizi ya Mraba
Kutatua equations radical
Katika mazoezi yafuatayo, tatua equation.
\(\sqrt{7z+1}=6\)
- Jibu
-
5
\(\sqrt{4u−2}−4=0\)
\(\sqrt{6m+4}−5=0\)
- Jibu
-
\(\frac{7}{2}\)
\(\sqrt{2u−3}+2=0\)
\(\sqrt{u−4}+4=u\)
- Jibu
-
hakuna suluhisho
\(\sqrt{v−9}+9=0\)
\(\sqrt{r−4}−r=−10\)
- Jibu
-
13
\(\sqrt{s−9}−s=−9\)
\(2\sqrt{2x−7}−4=8\)
- Jibu
-
\(\frac{43}{2}\)
\(\sqrt{2−x}=\sqrt{2x−7}\)
\(\sqrt{a}+3=\sqrt{a+9}\)
- Jibu
-
0
\(\sqrt{r}+3=\sqrt{r+4}\)
\(\sqrt{u}+2=\sqrt{u+5}\)
- Jibu
-
\(\frac{11}{6}\)
\(\sqrt{n+11}−1=\sqrt{n+4}\)
\(\sqrt{y+5}+1=\sqrt{2y+3}\)
- Jibu
-
11
Katika mazoezi yafuatayo, tatua. Round makadirio ya mahali moja decimal.
Kipande cha sod kitafunika eneo la futi za mraba 600. Trinh anataka kuagiza godoro la sod kufanya lawn mraba katika mashamba yake. Kutumia formula\(s=\sqrt{A}\) kupata urefu wa kila upande wa lawn yake.
Helikopta imeshuka mfuko kutoka kimo cha miguu 900 juu ya hiker stranded. Tumia formula\(t=\frac{\sqrt{h}}{4}\) ili kupata sekunde ngapi ilichukua kwa mfuko ili kufikia hiker.
- Jibu
-
Sekunde 7.5
Afisa Morales alipima alama za skid za moja ya magari yaliyohusika katika ajali. Urefu wa alama za skid ulikuwa miguu 245. Tumia formula\(s=\sqrt{24d}\) ili kupata kasi ya gari kabla ya breki zilitumiwa.
Mizizi ya Juu
Rahisisha Maneno na Mizizi ya Juu
Katika mazoezi yafuatayo, kurahisisha.
- \(\sqrt[6]{64}\)
- \(\sqrt[3]{64}\)
- Jibu
-
- 2
- 4
- \(\sqrt[3]{−27}\)
- \(\sqrt[4]{−64}\)
- \(\sqrt[9]{d^9}\)
- \(\sqrt[8]{v^8}\)
- Jibu
-
- d
- |v|
- \(\sqrt[5]{a^{10}}\)
- \(\sqrt[3]{b^{27}}\)
- \(\sqrt[4]{16x^8}\)
- \(\sqrt[6]{64y^{12}}\)
- Jibu
-
- \(2x^2\)
- \(2y^2\)
- \(\sqrt[7]{128r^{14}}\)
- \(\sqrt[4]{81s^{24}}\)
Tumia Mali ya Bidhaa ili kurahisisha Maneno na Mizizi ya Juu
Katika mazoezi yafuatayo, kurahisisha.
- \(\sqrt[9]{d^9}\)
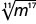
- Jibu
-
- d
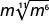
- \(\sqrt[3]{54}\)
- \(\sqrt[4]{128}\)
- \(\sqrt[5]{64c^8}\)
- \(\sqrt[4]{48d^7}\)
- Jibu
-
- \(2c\sqrt[5]{2c^3}\)
- \(2d\sqrt[4]{3d^3}\)
- \(\sqrt[3]{343q^7}\)
- \(\sqrt[6]{192r^9}\)
- \(\sqrt[3]{−500}\)
- \(\sqrt[4]{−16}\)
- Jibu
-
- \(−5\sqrt[3]{4}\)
- si idadi halisi
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt[5]{\frac{r^{10}}{r^5}}\)
\(\sqrt[3]{\frac{w^{12}}{w^2}}\)
- Jibu
-
\(w^3\sqrt[3]{w}\)
\(\sqrt[4]{\frac{64y^8}{4y^5}}\)
\(\sqrt[3]{\frac{54z^9}{2z^3}}\)
- Jibu
-
\(3z^2\)
\(\sqrt[6]{\frac{64a^7}{b^2}}\)
Katika mazoezi yafuatayo, kurahisisha.
\(4\sqrt[5]{20}−2\sqrt[5]{20}\)
- Jibu
-
\(2\sqrt[5]{20}\)
\(4\sqrt[3]{18}+3\sqrt[3]{18}\)
\(\sqrt[4]{1250}−\sqrt[4]{162}\)
- Jibu
-
\(2\sqrt[4]{2}\)
\(\sqrt[3]{640c^5}−\sqrt[3]{−80c^3}\)
\(\sqrt[5]{96t^8}+\sqrt[5]{486t^4}\)
- Jibu
-
\(2t^\sqrt[5]{3t^3}+3\sqrt[5]{2t^4}\)
Mantiki watetezi
Kurahisisha Maneno na\(a^{\frac{1}{n}}\)
Katika mazoezi yafuatayo, andika kama kujieleza kwa kiasi kikubwa.
\(r^{\frac{1}{8}}\)
\(s^{\frac{1}{10}}\)
- Jibu
-
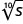
Katika mazoezi yafuatayo, andika kwa ufafanuzi wa busara.
\(\sqrt[5]{u}\)
\(\sqrt[6]{v}\)
- Jibu
-
\(v^{\frac{1}{6}}\)
\(\sqrt[3]{9m}\)
\(\sqrt[6]{10z}\)
- Jibu
-
\((10z)^{\frac{1}{6}}\)
Katika mazoezi yafuatayo, kurahisisha.
\(16^{\frac{1}{4}}\)
\(32^{\frac{1}{5}}\)
- Jibu
-
2
\((−125)^{\frac{1}{3}}\)
\((125)^{−\frac{1}{3}}\)
- Jibu
-
\(\frac{1}{5}\)
\((−9)^{\frac{1}{2}}\)
\((36)^{−\frac{1}{2}}\)
- Jibu
-
\(\frac{1}{6}\)
Katika mazoezi yafuatayo, andika kwa ufafanuzi wa busara.
\(\sqrt[3]{q^5}\)
\(\sqrt[5]{n^8}\)
- Jibu
-
\(n^{\frac{8}{5}}\)
Katika mazoezi yafuatayo, kurahisisha.
\(27^{−\frac{2}{3}}\)
\(64^{\frac{5}{2}}\)
- Jibu
-
32,768
\(36^{\frac{3}{2}}\)
\(81^{−\frac{5}{2}}\)
- Jibu
-
\(\frac{1}{59,049}\)
Tumia Sheria za Watazamaji ili kurahisisha Maneno na Maonyesho ya Mantiki
Katika mazoezi yafuatayo, kurahisisha.
\(3^{\frac{4}{5}}·3^{\frac{6}{5}}\)
\((x^6)^{\frac{4}{3}}\)
- Jibu
-
\(x^8\)
\(\frac{z^{\frac{5}{2}}}{z^{\frac{7}{5}}}\)
\((16s^{\frac{9}{4}})^{\frac{1}{4}}\)
- Jibu
-
\(2s^{\frac{9}{16}}\)
\((m^{8}n^{12})^{\frac{1}{4}}\)
\(\frac{z^{\frac{2}{3}}·z^{−\frac{1}{3}}}{z^{−\frac{5}{3}}}\)
- Jibu
-
\(z^2\)
Mazoezi mtihani
Katika mazoezi yafuatayo, kurahisisha.
\(\sqrt{81+144}\)
\(\sqrt{169m^{4}n^{2}}\)
- Jibu
-
\(13m^{2}|n|\)
\(\sqrt{36n^{13}}\)
\(3\sqrt{13}+5\sqrt{2}+\sqrt{13}\)
- Jibu
-
\(4\sqrt{13}+5\sqrt{2}\)
\(5\sqrt{20}+2\sqrt{125}\)
\((3\sqrt{6y})(\sqrt{250y^3})\)
- Jibu
-
\(180y^2\sqrt{3}\)
\((2−5\sqrt{x})(3+\sqrt{x})\)
\((1−2\sqrt{q})^2\)
- Jibu
-
\(1−4\sqrt{q}+4q\)
- \(\sqrt{a^{12}}\)
- \(\sqrt[3]{b^{21}}\)
- \(\sqrt[4]{81x^{12}}\)
- \(\sqrt[6]{64y^{18}}\)
- Jibu
-
- \(3x^3\)
- \(2y^3\)
\(\sqrt[6]{\frac{64r^{12}}{25r^6}}\)
\(\sqrt{\frac{14y^3}{7y}}\)
- Jibu
-
\(y\sqrt{2}\)
\(\frac{\sqrt{256x^7}}{\sqrt{54x^2}}\)
\(\sqrt[4]{512}−2\sqrt[4]{32}\)
- Jibu
-
0
- \(256^{\frac{1}{4}}\)
- \(243^{\frac{1}{5}}\)
\(49^{\frac{3}{2}}\)
- Jibu
-
343
\(25^{−\frac{5}{2}}\)
\(\frac{w^{\frac{3}{4}}}{w^{\frac{7}{4}}}\)
- Jibu
-
\(\frac{1}{w}\)
\((27s^{\frac{3}{5}})^{\frac{1}{3}}\)
Katika mazoezi yafuatayo, rationalize denominator.
\(\frac{3}{2\sqrt{6}}\)
- Jibu
-
\(\frac{\sqrt{6}}{4}\)
\(\frac{\sqrt{3}}{\sqrt{x}+\sqrt{5}}\)
Katika mazoezi yafuatayo, tatua.
\(3\sqrt{2x−3}−20=7\)
- Jibu
-
42
\(\sqrt{3u−2}=\sqrt{5u+1}\)
Katika zoezi zifuatazo, tatua.
helikopta flying katika urefu wa 600 miguu imeshuka mfuko kwa lifeboat. Tumia formula\(t=\frac{\sqrt{h}}{4}\) ili kupata sekunde ngapi ilichukua kwa mfuko ili kufikia hiker. Pindua jibu lako kwa karibu kumi ya pili.
- Jibu
-
6.1 sekunde


