Sura ya 8 Mazoezi Mapitio
- Page ID
- 177699
Sura ya Mapitio ya mazoezi
Kurahisisha maneno ya busara
Tambua Maadili ambayo Ufafanuzi wa busara haukufafanuliwa
Katika mazoezi yafuatayo, tambua maadili ambayo maneno ya busara hayajafafanuliwa.
\(\dfrac{2a+1}{3a−2}\)
- Jibu
-
\(a \ne \dfrac{2}{3}\)
\(\dfrac{b−3}{b^2−16}\)
\(\dfrac{3xy^2}{5y}\)
- Jibu
-
\(y \ne 0\)
\(\dfrac{u−3}{u^2−u−30}\)
Tathmini Maneno ya busara
Katika mazoezi yafuatayo, tathmini maneno ya busara kwa maadili yaliyotolewa.
\(\dfrac{4p−1}{p^2+5}\)lini\(p=−1\)
- Jibu
-
\(−\dfrac{5}{6}\)
\(\dfrac{q^2−5}{q+3}\)lini\(q=7\)
\(\dfrac{y^2−8}{y^2−y−2}\)lini\(y=1\)
- Jibu
-
\(\dfrac{7}{2}\)
\(\dfrac{z^2+2}{4z−z^2}\)lini\(z=3\)
Katika mazoezi yafuatayo, kurahisisha.
\(\dfrac{10}{24}\)
- Jibu
-
\(\dfrac{5}{12}\)
\(\dfrac{8m^4}{16mn^3}\)
\(\dfrac{14a−14}{a−1}\)
- Jibu
-
\(14\)
\(\dfrac{b^2+7b+12}{b^2+8b+16}\)
Kurahisisha maneno ya busara na Mambo ya kinyume
Katika mazoezi yafuatayo, kurahisisha.
\(\dfrac{c^2−c−2}{4−c^2}\)
- Jibu
-
\(-\dfrac{c+1}{c+2}\)
\(\dfrac{d−16}{16−d}\)
\(\dfrac{7v−35}{25−v^2}\)
- Jibu
-
\(−\dfrac{7}{5+v}\)
\(\dfrac{w^2−3w−28}{49−w^2}\)
Panua na Gawanya Maneno ya busara
Kuzidisha maneno ya busara
Katika mazoezi yafuatayo, ongeze.
\(\dfrac{3}{8}·\dfrac{2}{15}\)
- Jibu
-
\(\dfrac{1}{20}\)
\(\dfrac{2xy^2}{8y^3}·\dfrac{16y}{24x}\)
\(\dfrac{3a^2+21a}{a^2+6a−7}·\dfrac{a−1}{ab}\)
- Jibu
-
\(\dfrac{3}{b}\)
\(\dfrac{5z^2}{5z^2+40z+35}·\dfrac{z^2−1}{3z}\)
Gawanya Maneno ya busara
Katika mazoezi yafuatayo, ugawanye.
\(\dfrac{t^2−4t-12}{t^2+8t+12}÷\dfrac{t^2−36}{6t}\)
- Jibu
-
\(\dfrac{6t}{(t+6)^2}\)
\(\dfrac{r^2−16}{4}÷\dfrac{r^3−64}{2r^2−8r+32}\)
\(\dfrac{11+w}{w−9}÷\dfrac{121−w^2}{9−w}\)
- Jibu
-
\(\dfrac{1}{11+w}\)
\(\dfrac{3y^2−12y−63}{4y+3}÷(6y^2−42y)\)
\(\dfrac{\dfrac{c^2−64}{3c^2+26c+16}}{\dfrac{c^2−4c−32}{15c+10}}\)
- Jibu
-
\(5c+4\)
\(\dfrac{8m^2−8m}{m−4}·\dfrac{m^2+2m−24}{m^2+7m+10}÷\dfrac{2m^2−6m}{m+5}\)
Ongeza na Ondoa Maneno ya busara na Denominator ya kawaida
Ongeza Maneno ya busara na Denominator ya kawaida
Katika mazoezi yafuatayo, ongeza.
\(\dfrac{3}{5}+\dfrac{2}{5}\)
- Jibu
-
\(1\)
\(\dfrac{4a^2}{2a−1}−\dfrac{1}{2a−1}\)
\(\dfrac{p^2+10p}{p+5}+\dfrac{25}{p+5}\)
- Jibu
-
\(p+5\)
\(\dfrac{3x}{x−1}+\dfrac{2}{x−1}\)
Ondoa Maneno ya busara na Denominator ya kawaida
Katika mazoezi yafuatayo, toa.
\(\dfrac{d^2}{d+4}−\dfrac{3d+28}{d+4}\)
- Jibu
-
\(d-7\)
\(\dfrac{z^2}{z+10}−\dfrac{100}{z+10}\)
\(\dfrac{4q^2−q+3}{q^2+6q+5}−\dfrac{3q^2+q+6}{q^2+6q+5}\)
- Jibu
-
\(\dfrac{q−3}{q+5}\)
\(\dfrac{5t+4t+3}{t^2−25}−\dfrac{4t^2−8t−32}{t^2−25}\)
Katika mazoezi yafuatayo, ongeza na uondoe.
\(\dfrac{18w}{6w−1}+\dfrac{3w−2}{1−6w}\)
- Jibu
-
\(\dfrac{15w+2}{6w−1}\)
\(\dfrac{a^2+3a}{a^2−4}−\dfrac{3a−8}{4−a^2}\)
\(\dfrac{2b^2+3b−15}{b^2−49}−\dfrac{b^2+16b−1}{49−b^2}\)
- Jibu
-
\(\dfrac{3b−2}{b+7}\)
\(\dfrac{8y^2−10y+7}{2y−5}+\dfrac{2y^2+7y+2}{5−2y}\)
Ongeza na Ondoa Maneno ya busara Kwa Tofauti na Denominators
Pata Denominator ya kawaida ya maneno ya busara
Katika mazoezi yafuatayo, pata LCD.
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\)
- Jibu
-
\((m+2)(m−5)(m+4)\)
\(\dfrac{6}{n^2−4},\quad\dfrac{2n}{n^2−4n+4}\)
\(\dfrac{5}{3p^2+17p−6},\quad\dfrac{2m}{3p^2−23p−8}\)
- Jibu
-
\((3p+1)(p+6)(p+8)\)
Katika mazoezi yafuatayo, andika upya kama maneno sawa ya busara na denominator iliyotolewa.
Andika upya kama maneno sawa ya busara na denominator\((m+2)(m−5)(m+4)\)
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\).
Andika upya kama maneno sawa ya busara na denominator\((n−2)(n−2)(n+2)\)
\(\dfrac{6}{n^2−4n+4},\quad\dfrac{2n}{n^2−4}\).
- Jibu
-
\(\dfrac{6n+12}{(n−2)(n−2)(n+2)},\quad\dfrac{2n^2−4n}{(n−2)(n−2)(n+2)}\)
Andika upya kama maneno sawa ya busara na denominator\((3p+1)(p+6)(p+8)\)
\(\dfrac{5}{3p^2+19p+6},\quad\dfrac{7p}{3p^2+25p+8}\)
Katika mazoezi yafuatayo, ongeza.
\(\dfrac{2}{3}+\dfrac{3}{5}\)
- Jibu
-
\(\dfrac{19}{15}\)
\(\dfrac{7}{5a}+\dfrac{3}{2b}\)
\(\dfrac{2}{c−2}+\dfrac{9}{c+3}\)
- Jibu
-
\(\dfrac{11c−12}{(c−2)(c+3)}\)
\(\dfrac{3d}{d^2−9}+\dfrac{5}{d^2+6d+9}\)
\(\dfrac{2x}{x^2+10x+24}+\dfrac{3x}{x^2+8x+16}\)
- Jibu
-
\(\dfrac{5x^2+26x}{(x+4)(x+4)(x+6)}\)
\(\dfrac{5q}{p^{2}q−p^2}+\dfrac{4q}{q^2−1}\)
Katika mazoezi yafuatayo, toa na uongeze.
\(\dfrac{3v}{v+2}−\dfrac{v+2}{v+8}\)
- Jibu
-
\(\dfrac{2(v^2+10v−2)}{(v+2)(v+8)}\)
\(\dfrac{−3w−15}{w^2+w−20}−\dfrac{w+2}{4−w}\)
\(\dfrac{7m+3}{m+2}−5\)
- Jibu
-
\(\dfrac{2m−7}{m+2}\)
\(\dfrac{n}{n+3}+\dfrac{2}{n−3}−\dfrac{n−9}{n^2−9}\)
\(\dfrac{8d}{d^2−64}−\dfrac{4}{d+8}\)
- Jibu
-
\(4d−8\)
\(\dfrac{5}{12x^{2}y}+\dfrac{7}{20xy^3}\)
Kurahisisha Maneno ya busara
Kurahisisha Complex Muhtasari kujieleza kwa kuandika kama Idara
Katika mazoezi yafuatayo, kurahisisha.
\(\dfrac{\dfrac{5a}{a+2}}{\dfrac{10a^2}{a^2−4}}\)
- Jibu
-
\(\dfrac{a−2}{2a}\)
\(\dfrac{\dfrac{2}{5}+\dfrac{5}{6}}{\dfrac{1}{3}+\dfrac{1}{4}}\)
\(\dfrac{x−\dfrac{3x}{x+5}}{\dfrac{1}{x+5}+\dfrac{1}{x−5}}\)
- Jibu
-
\(\dfrac{(x−8)(x−5)}{2}\)
\(\dfrac{\dfrac{2}{m}+\dfrac{m}{n}}{\dfrac{n}{m}−\dfrac{1}{n}}\)
Katika mazoezi yafuatayo, kurahisisha.
\(\dfrac{6+\dfrac{2}{q−4}}{\dfrac{5}{q}+4}\)
- Jibu
-
\(\dfrac{(q−2)(q+4)}{5(q−4)}\)
\(\dfrac{\dfrac{3}{a^2}−\dfrac{1}{b}}{\dfrac{1}{a}+\dfrac{1}{b^2}}\)
\(\dfrac{\dfrac{2}{z^2−49}+\dfrac{1}{z+7}}{\dfrac{9}{z+7}+\dfrac{12}{z−7}}\)
- Jibu
-
\(\dfrac{z−5}{21z+21}\)
\(\dfrac{\dfrac{3}{y^2−4y−32}}{\dfrac{2}{y−8}+\dfrac{1}{y+4}}\)
Kutatua milinganyo ya busara
Kutatua milinganyo ya busara
Katika mazoezi yafuatayo, tatua.
\(\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{1}{x}\)
- Jibu
-
\(\dfrac{6}{7}\)
\(1−\dfrac{2}{m}=\dfrac{8}{m^2}\)
\(\dfrac{1}{b−2}+\dfrac{1}{b+2}=\dfrac{3}{b^2−4}\)
- Jibu
-
\(\dfrac{3}{2}\)
\(\dfrac{3}{q+8}−\dfrac{2}{q−2}=1\)
\(\dfrac{v−15}{v^2−9v+18}=\dfrac{4}{v−3}+\dfrac{2}{v−6}\)
- Jibu
-
hakuna suluhisho
\(\dfrac{z}{12}+\dfrac{z+3}{3z}=\dfrac{1}{z}\)
Tatua usawa wa busara kwa Variable Maalum
Katika mazoezi yafuatayo, tatua kwa kutofautiana iliyoonyeshwa.
\(\dfrac{V}{l}=hw\)kwa\(l\)
- Jibu
-
\(l=\dfrac{V}{hw}\)
\(\dfrac{1}{x}−\dfrac{2}{y}=5\)kwa\(y\)
\(x=\dfrac{y+5}{z−7}\)kwa\(z\)
- Jibu
-
\(z=\dfrac{y+5+7x}{x}\)
\(P=\dfrac{k}{V}\)kwa\(V\)
Kutatua Uwiano na Sawa Kielelezo Maombi Ufanana
Kutatua idadi
Katika mazoezi yafuatayo, tatua.
\(\dfrac{x}{4}=\dfrac{3}{5}\)
- Jibu
-
\(\dfrac{12}{5}\)
\(\dfrac{3}{y}=\dfrac{9}{5}\)
\(\dfrac{s}{s+20}=\dfrac{3}{7}\)
- Jibu
-
\(15\)
\(\dfrac{t−3}{5}=\dfrac{t+2}{9}\)
Katika mazoezi yafuatayo, tatua kutumia uwiano.
Rachael alikuwa\(21\) ounce strawberry kuitingisha ambayo ina\(739\) kalori. Kuna kalori ngapi katika kuitingisha kwa\(32\) ounce?
- Jibu
-
\(1161\)kalori
Leo akaenda Mexico juu ya mapumziko ya Krismasi na kubadilisha\($525\) dola katika peso Mexican. Wakati huo, kiwango cha ubadilishaji alikuwa\($1\) Marekani ni sawa na peso ya\(16.25\) Mexican. Alipata peso ngapi za Mexico kwa safari yake?
Katika mazoezi yafuatayo, tatua.
\(∆ABC\)ni sawa na\(∆XYZ\). Urefu wa pande mbili za kila pembetatu hutolewa katika takwimu. Pata urefu wa pande za tatu.
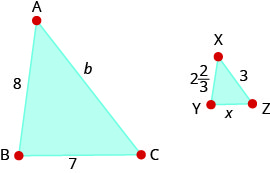
- Jibu
-
\(b=9\);\(x=2\dfrac{1}{3}\)
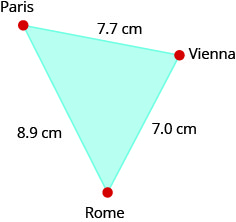
Katika ramani ya Ulaya, Paris, Roma, na Vienna huunda pembetatu ambayo pande zake zinaonyeshwa kwenye takwimu hapa chini. Ikiwa umbali halisi kutoka Roma hadi Vienna ni\(700\) maili, pata umbali kutoka
- Paris hadi Roma
- b Paris hadi Vienna
Tony ni\(5.75\) miguu mirefu. Mwishoni mwa mchana mmoja, kivuli chake kilikuwa\(8\) miguu ndefu. Wakati huo huo, kivuli cha mti wa karibu kilikuwa\(32\) miguu ndefu. Pata urefu wa mti.
- Jibu
-
\(23\)miguu
Urefu wa lighthouse huko Pensacola, Florida ni\(150\) miguu. Kusimama karibu na sanamu,\(5.5\) mguu mrefu Natalie kutupwa kivuli\(1.1\) mguu muda gani kivuli cha lighthouse kuwa?
Tatua Matatizo ya Maombi ya Uniform na Kazi
Kutatua maombi ya mwendo Sare
Katika mazoezi yafuatayo, tatua.
Wakati wa kufanya gari la saa 5 nyumbani kwa kutembelea wazazi wake, Lisa alikimbia katika hali mbaya ya hewa. Aliweza kuendesha\(176\) maili wakati hali ya hewa ilikuwa nzuri, lakini kisha kuendesha gari\(10\) mph polepole, akaenda\(81\) maili katika hali mbaya ya hewa. Aliendesha gari kwa kasi gani wakati hali ya hewa ilikuwa mbaya?
- Jibu
-
45 mph
Mark ni wanaoendesha ndege ambayo inaweza kuruka\(490\) maili na tailwind ya\(20\) mph wakati huo huo kwamba inaweza kuruka\(350\) maili dhidi tailwind ya\(20\) mph. Kasi ya ndege ni nini?
John anaweza wapanda baiskeli\(8\) mph yake kwa kasi zaidi kuliko Luka unaweza wapanda baiskeli Inachukua muda mrefu wa\(3\) masaa Luke kuliko John kuendesha\(48\) maili. Jinsi ya kufunga unaweza John wapanda baiskeli yake?
- Jibu
-
\(16\)mph
Mark alikuwa mafunzo kwa triathlon. Alikimbia\(8\) kilomita na\(32\) kilomita za baiskeli kwa jumla ya\(3\) masaa. Kasi yake ya kukimbia ilikuwa\(8\) kilomita kwa saa chini ya kasi yake ya baiskeli. Je! Kasi yake ya mbio ilikuwa nini?
Katika mazoezi yafuatayo, tatua.
Jerry unaweza sura chumba katika\(1\) saa, wakati Jake inachukua\(4\) masaa. Je! Wangeweza kuunda chumba cha kufanya kazi pamoja?
- Jibu
-
\(\dfrac{4}{5}\)saa
Lisa inachukua\(3\) masaa ya mow lawn wakati binamu yake, Barb, inachukua\(2\) masaa. Itachukua muda gani kufanya kazi pamoja?
Jeffrey anaweza kuchora nyumba kwa\(6\) siku, lakini kama anapata msaidizi anaweza kufanya hivyo kwa\(4\) siku. Itachukua muda gani msaidizi wa kuchora nyumba peke yake?
- Jibu
-
\(12\)siku
Sue na Deb hufanya kazi pamoja wakiandika kitabu kinachochukua\(90\) siku. Kama Sue kazi peke yake itachukua\(120\) siku zake. Itachukua muda gani Deb kuandika kitabu peke yake?
Tumia Tofauti ya moja kwa moja na Inverse
Tatua matatizo ya Tofauti ya moja kwa moja
Katika mazoezi yafuatayo, tatua.
Kama\(y\) inatofautiana moja kwa moja kama\(x\), wakati\(y=9\) na\(x=3\), kupata\(x\) wakati\(y=21\).
- Jibu
-
\(7\)
Kama\(y\) inatofautiana moja kwa moja kama\(x\), wakati\(y=20\) na\(x=2\), kupata\(y\) wakati\(x=4\).
Kama\(m\) inatofautiana inversely na mraba wa\(n\), wakati\(m=4\) na\(n=6\), kupata\(m\) wakati\(n=2\).
- Jibu
-
\(36\)
Vanessa anasafiri kumwona mchumba wake. umbali\(d\), inatofautiana moja kwa moja na kasi\(v\), yeye anatoa. Kama yeye husafiri\(258\) maili kuendesha gari\(60\) mph, umbali gani yeye kusafiri kwenda\(70\) mph?
Kama gharama ya pizza inatofautiana moja kwa moja na kipenyo chake, na kama\(8\) “kipenyo pizza gharama\($12\), ni kiasi gani\(6\)” kipenyo pizza gharama?
- Jibu
-
\($9\)
Umbali wa kuacha gari unatofautiana moja kwa moja na mraba wa kasi yake. Inachukua\(200\) miguu kuacha gari kwenda\(50\) mph. Ngapi miguu ingekuwa kuchukua kuacha gari kwenda\(60\) mph?
Katika mazoezi yafuatayo, tatua.
Idadi ya tiketi kwa kuchangisha muziki inatofautiana inversely na bei ya tiketi. Ikiwa Madelyn ana pesa za kutosha kununua\(12\) tiketi\($6\), ni tiketi ngapi ambazo Madelyn zinaweza kumudu kununua ikiwa bei imeongezeka hadi\($8\)?
- Jibu
-
\(97\)tiketi
Kwenye chombo cha kamba, urefu wa kamba hutofautiana kinyume na mzunguko wa vibrations zake. Ikiwa kamba\(11\) -inch kwenye violin ina mzunguko wa\(360\) mizunguko kwa sekunde, ni mzunguko gani\(12\) -inch kamba ina?
Mazoezi mtihani
Katika mazoezi yafuatayo, kurahisisha.
\(\dfrac{3a^{2}b}{6ab^2}\)
- Jibu
-
\(\dfrac{a}{2b}\)
\(\dfrac{5b−25}{b^2−25}\)
Katika mazoezi yafuatayo, fanya operesheni iliyoonyeshwa na kurahisisha.
\(\dfrac{4x}{x+2}·\dfrac{x^2+5x+6}{12x^2}\)
- Jibu
-
\(\dfrac{x+3}{3x}\)
\(\dfrac{5y}{4y−8}·\dfrac{y^2−4}{10}\)
\(\dfrac{4p}{q}+\dfrac{5}{p}\)
- Jibu
-
\(\dfrac{4+5q}{pq}\)
\(\dfrac{1}{z−9}−\dfrac{3}{z+9}\)
\(\dfrac{\dfrac{2}{3}+\dfrac{3}{5}}{\dfrac{2}{5}}\)
- Jibu
-
\(\dfrac{19}{16}\)
\(\dfrac{\dfrac{1}{m}−\dfrac{1}{n}}{\dfrac{1}{n}+\dfrac{1}{m}}\)
Katika mazoezi yafuatayo, tatua kila equation.
\(\dfrac{1}{2}+\dfrac{2}{7}=\dfrac{1}{x}\)
- Jibu
-
\(x = \dfrac{14}{11}\)
\(\dfrac{5}{y−6}=\dfrac{3}{y+6}\)
\(\dfrac{1}{z−5}+\dfrac{1}{z+5}=\dfrac{1}{z^2−25}\)
- Jibu
-
\(z = \dfrac{1}{2}\)
\(\dfrac{t}{4}=\dfrac{3}{5}\)
\(\dfrac{2}{r−2}=\dfrac{3}{r−1}\)
- Jibu
-
\(r = 4\)
Katika mazoezi yafuatayo, tatua.
Kama\(y\) inatofautiana moja kwa moja na\(x\), na\(x=5\) wakati\(y=30\), kupata\(x\) wakati\(y=42\).
Kama\(y\) inatofautiana inversely\(x\) na na\(x=6\) wakati\(y=20\), kupata\(y\) wakati\(x=2\).
- Jibu
-
\(y=60\)
Kama\(y\) inatofautiana inversely na mraba wa\(x\) na\(x=3\) wakati\(y=9\), kupata\(y\) wakati\(x=4\).
Kipimo cha erythromycin kilichopendekezwa kwa mbwa, ni\(5\) mg kwa kila pound mbwa huzidi. Ikiwa Daisy ina uzito wa\(25\) paundi, ni miligramu ngapi za erythromycin anapaswa kuagiza daktari wake?
- Jibu
-
\(125\)mg
Julia alitumia\(4\) masaa Jumapili mchana utumiaji katika mazoezi. Yeye mbio juu ya treadmill kwa\(10\) maili na kisha baiskeli kwa\(20\) maili. Biking yake kasi ilikuwa\(5\) mph kasi zaidi kuliko mbio kasi yake juu ya treadmill. Je! Kasi yake ya mbio ilikuwa nini?
Kurt anaweza kuendesha baiskeli yake kwa\(30\) maili na upepo kwa kiasi hicho cha muda kwamba anaweza kwenda\(21\) maili dhidi ya upepo. Ikiwa kasi ya upepo ni\(6\) mph, kasi ya Kurt kwenye baiskeli yake ni nini?
- Jibu
-
\(14\)mph
Amanda jogs kwa\(8\) maili mbuga kwa kutumia njia moja na kisha anarudi kupitia njia\(14\) -maili. Safari ya kurudi inachukua\(1\) saa yake kwa muda mrefu kuliko jog yake kwenye hifadhi. Kupata kiwango cha jogging yake.
Washer wa dirisha mwenye ujuzi anaweza kuosha madirisha yote katika nyumba ya Mike kwa\(2\) masaa, wakati mwanafunzi mpya anaweza kuosha madirisha yote kwa\(7\) masaa. Je, itawachukua muda gani kufanya kazi pamoja?
- Jibu
-
\(1\frac{5}{9}\)saa
Josh unaweza kupasuliwa truckload ya magogo katika\(8\) masaa, lakini kufanya kazi na baba yake wanaweza kupata kufanyika katika\(3\) masaa. Je, itachukua muda gani baba wa Josh kufanya kazi peke yake ili kugawanya magogo?
Bei ambayo Tyler hulipia gesi inatofautiana moja kwa moja na idadi ya galoni anayenunua. Kama\(24\) galoni gharama yake\($59.76\), nini\(30\) galoni gharama?
- Jibu
-
\($74.70\)
Kiasi cha gesi katika chombo kinatofautiana kinyume na shinikizo la gesi. Ikiwa chombo cha nitrojeni kina kiasi cha\(29.5\) lita na\(2000\) psi, ni kiasi gani ikiwa tank ina kiwango cha\(14.7\) psi? Pande zote kwa nambari nzima iliyo karibu.
Miji ya Dayton, Columbus, na Cincinnati huunda pembetatu kusini mwa Ohio, kama inavyoonekana kwenye takwimu hapa chini, ambayo inatoa umbali wa ramani kati ya miji hii kwa inchi.
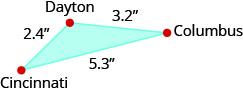
umbali halisi kutoka Dayton kwa Cincinnati ni\(48\) maili. ni umbali halisi kati ya Dayton na Columbus nini?
- Jibu
-
\(64\)maili