7.6E: Mazoezi

Last updated
Save as PDF

Page ID: 177515

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Mazoezi hufanya kamili

Tumia mali ya Bidhaa ya Zero

Katika mazoezi yafuatayo, tatua.

Zoezi 1

$(x−3)(x+7)=0$

Jibu: $x=3$,$x=−7$ hivyo kuweka suluhisho ni:$\{3, -7\}$

Zoezi la 2

$(y−11)(y+1)=0$

Zoezi la 3

$(3a−10)(2a−7)=0$

Jibu: $a=\frac{10}{3}$,$a=\frac{7}{2}$ hivyo kuweka suluhisho ni:$\Big\{\tfrac{10}{3}, \tfrac{7}{2}\Big\}$

Zoezi la 4

$(5b+1)(6b+1)=0$

Zoezi 5

$6m(12m−5)=0$

Jibu: $m=0$,$m=\frac{5}{12}$ hivyo kuweka suluhisho ni:$\Big\{0, \tfrac{5}{12}\Big\}$

Zoezi la 6

$2x(6x−3)=0$

Zoezi la 7

$(y−3)^2=0$

Jibu: $y=3$hivyo kuweka suluhisho ni:$\{3\}$

Zoezi 8

$(b+10)^2=0$

Zoezi la 9

$(2x−1)^2=0$

Jibu: $x=\frac{1}{2}$hivyo kuweka suluhisho ni:$\Big\{\tfrac{1}{2}\Big\}$

Zoezi 10

$(3y+5)^2=0$

Tatua Ulinganisho wa Quadratic kwa kuzingatia

Katika mazoezi yafuatayo, tatua.

Zoezi 11

$x^2+7x+12=0$

Jibu: $x=−3$,$x=−4$ hivyo kuweka suluhisho ni:$\{-3, -4\}$

Zoezi 12

$y^2−8y+15=0$

Zoezi 13

$5a^2−26a=24$

Jibu: $a=−\tfrac{4}{5}$,$a=6$ hivyo kuweka suluhisho ni:$\Big\{−\tfrac{4}{5}, 6\Big\}$

Zoezi 14

$4b^2+7b=−3$

Zoezi 15

$4m^2=17m−15$

Jibu: $m=\frac{5}{4}$,$m=3$ hivyo kuweka suluhisho ni:$\Big\{\tfrac{5}{4}, 3\Big\}$

Zoezi 16

$n^2=5−6n$

Zoezi 17

$7a^2+14a=7a$

Jibu: $a=−1$,$a=0$ hivyo kuweka suluhisho ni:$\{-1, 0\}$

Zoezi 18

$12b^2−15b=−9b$

Zoezi la 19

$49m^2=144$

Jibu: $m=\frac{12}{7}$,$m=−\frac{12}{7}$ hivyo kuweka suluhisho ni:$\Big\{−\tfrac{12}{7}, \tfrac{12}{7}\Big\}$

Zoezi la 20

$625=x^2$

Zoezi 21

$(y−3)(y+2)=4y$

Jibu: $y=−1$,$y=6$ hivyo kuweka suluhisho ni:$\{-1, 6\}$

Zoezi la 22

$(p−5)(p+3)=−7$

Zoezi 23

$(2x+1)(x−3)=−4x$

Jibu: $x=\frac{3}{2}$,$x=−1$ hivyo kuweka suluhisho ni:$\Big\{-1,\tfrac{3}{2}\Big\}$

Zoezi 24

$(x+6)(x−3)=−8$

Zoezi 25

$16p^3=24p^2−9p$

Jibu: $p=0$,$p=\frac{3}{4}$ hivyo kuweka suluhisho ni:$\Big\{0,\tfrac{3}{4}\Big\}$

Zoezi 26

$m^3−2m^2=−m$

Zoezi 27

$20x^2−60x=−45$

Jibu: $x=\frac{3}{2}$hivyo kuweka suluhisho ni:$\Big\{\tfrac{3}{2}\Big\}$

Zoezi 28

$3y^2−18y=−27$

Kutatua Maombi yanayotokana na equations Quadratic

Katika mazoezi yafuatayo, tatua.

Zoezi 29

Bidhaa ya integers mbili mfululizo ni 56. Pata integers.

Jibu: 7 na 8; -8 na -7

Zoezi 30

Bidhaa ya integers mbili mfululizo ni 42. Pata integers.

Zoezi 31

Eneo la carpet mstatili ni futi za mraba 28. Urefu ni miguu mitatu zaidi ya upana. Pata urefu na upana wa carpet.

Jibu: Miguu 4 na miguu 7

Zoezi 32

Ukuta wa kubakiza mstatili una eneo la miguu ya mraba 15. Urefu wa ukuta ni miguu miwili chini ya urefu wake. Pata urefu na urefu wa ukuta.

Zoezi la 33

Pennant ni umbo kama pembetatu ya kulia, na hypotenuse 10 miguu. Urefu wa upande mmoja wa pennant ni urefu wa miguu miwili kuliko urefu wa upande mwingine. Pata urefu wa pande mbili za pennant.

Jibu: Miguu 6 na miguu 8

Zoezi 34

Bwawa la kutafakari linaumbwa kama pembetatu ya kulia, na mguu mmoja kando ya ukuta wa jengo. Hypotenuse ni urefu wa miguu 9 kuliko upande wa jengo hilo. Upande wa tatu ni urefu wa miguu 7 kuliko upande kando ya jengo. Pata urefu wa pande zote tatu za bwawa la kutafakari.

Mazoezi ya mchanganyiko

Katika mazoezi yafuatayo, tatua.

Zoezi 35

(x+8) (x-3) =0

Jibu: $x=−8, \; x=3$hivyo kuweka suluhisho ni:$\{-8, 3\}$

Zoezi 36

(3y-5) (y+7) =0

Zoezi 37

$p^2+12p+11=0$

Jibu: $p=−1, \;p=−11$hivyo kuweka suluhisho ni:$\{-11, -1\}$

Zoezi 38

$q^2−12q−13=0$

Zoezi 39

$m^2=6m+16$

Jibu: $m=−2, \; m=8$hivyo kuweka suluhisho ni:$\{-2, 8\}$

Zoezi 40

$4n^2+19n=5$

Zoezi 41

$a^3−a^2−42a=0$

Jibu: $a=0, \;a=−6, \;a=7$hivyo kuweka suluhisho ni:$\{-6, 0, 7\}$

Zoezi 42

$4b^2−60b+224=0$

Zoezi 43

Bidhaa ya integers mbili mfululizo ni 110. Pata integers.

Jibu: 10 na 11; -11 na -10

Zoezi 44

Urefu wa mguu mmoja wa pembetatu ya kulia ni tatu zaidi kuliko mguu mwingine. Ikiwa hypotenuse ni 15, pata urefu wa miguu miwili.

kila siku Math

Zoezi 45

Eneo la patio Ikiwa kila upande wa patio ya mraba umeongezeka kwa miguu 4, eneo la patio itakuwa miguu ya mraba 196. Kutatua equation (s+4) 2=196 (s+4) 2=196 kwa s kupata urefu wa upande wa patio.

Jibu: Futi 10

Zoezi 46

Tone la Watermelon Watermelon imeshuka kutoka hadithi ya kumi ya jengo. Tatua equation -16t2+144=0,116t2+144=0 kwa tt ili kupata idadi ya sekunde inachukua watermelon kufikia ardhi.

Mazoezi ya kuandika

Zoezi 47

Eleza jinsi ya kutatua equation quadratic. Ni majibu ngapi unatarajia kupata equation quadratic?

Jibu: Majibu yanaweza kutofautiana kwa maelezo. Unapaswa kutarajia hakuna ufumbuzi zaidi ya 2 kwa equation quadratic. Mara nyingi ina ufumbuzi mbili, lakini wakati mwingine, inaweza kuwa na suluhisho moja kwa mara au hata hakuna suluhisho.

Zoezi 48

Kutoa mfano wa equation quadratic ambayo ina GCF na hakuna ufumbuzi wa equation ni sifuri.

Self Check

Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

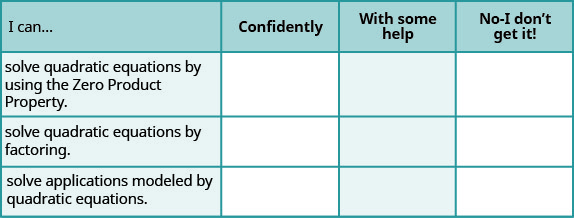
$Jedwali hili lina kauli zifuatazo zote kutanguliwa na “Naweza...”. Mstari wa kwanza ni “kutatua equations quadratic kwa kutumia mali ya bidhaa zero”. Mstari wa pili ni “kutatua equations quadratic kwa factoring”. Mstari wa tatu ni “kutatua maombi yaliyotokana na equations quadratic”. Katika nguzo kando ya kauli hizi ni vichwa, “kwa ujasiri”, “kwa msaada fulani”, na “Hakuna-siipati!”.$

b Kwa ujumla, baada ya kuangalia orodha, unafikiri umeandaliwa vizuri kwa ajili ya sehemu inayofuata? Kwa nini au kwa nini?