7.6: Ulinganifu wa Quadratic
- Page ID
- 177504
Mwishoni mwa sehemu hii, utaweza:
- Tatua equations quadratic kwa kutumia Zero Bidhaa Mali
- Kutatua equations quadratic factoring
- Tatua programu zinazoelekezwa na equations quadratic
Kabla ya kuanza, fanya jaribio hili la utayari.
- Kutatua:\(5y−3=0\).
Ikiwa umekosa tatizo hili, tathmini Zoezi 2.3.1. - Kutatua:\(10a=0\).
Ikiwa umekosa tatizo hili, tathmini Zoezi 2.2.1. - Kuchanganya kama maneno:\(12 x^{2}-6 x+4 x\).
Kama amekosa tatizo hili, kupitia Zoezi 1.3.37. - Sababu\(n^{3}-9 n^{2}-22 n\) kabisa.
Kama amekosa tatizo hili, kupitia Zoezi 7.3.10.
Tayari tumetatua equations linear, equations ya fomu\(a x+b y=c\). Katika equations linear, vigezo hawana exponents. Ulinganisho wa Quadratic ni equations ambayo variable ni mraba. Imeorodheshwa hapa chini ni baadhi ya mifano ya equations quadratic:
\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]
equation mwisho haionekani kuwa na squared variable, lakini wakati sisi kurahisisha kujieleza upande wa kushoto sisi kupata\(n^{2}+n\).
Aina ya jumla ya equation quadratic ni\(a x^{2}+b x+c=0\), na\(a \neq 0\).
Equation ya fomu\(a x^{2}+b x+c=0\) inaitwa equation quadratic.
\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]
Ili kutatua equations quadratic tunahitaji mbinu tofauti na yale tuliyotumia katika kutatua equations linear. Tutaangalia njia moja hapa na kisha wengine kadhaa katika sura ya baadaye.
Tatua Ulinganisho wa Quadratic Kutumia Mali ya Bidhaa ya Zero
Sisi kwanza kutatua equations quadratic kwa kutumia Zero Bidhaa Mali. Mali ya Bidhaa ya Zero inasema kwamba ikiwa bidhaa ya kiasi mbili ni sifuri, lazima iwe kwamba angalau moja ya kiasi ni sifuri. Njia pekee ya kupata bidhaa sawa na sifuri ni kuzidi kwa sifuri yenyewe.
\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)
Sasa tutatumia mali ya Bidhaa ya Zero, ili kutatua equation ya quadratic.
Kutatua:\((x+1)(x-4)=0\)
- Jibu
-



Kutatua:\((x-3)(x+5)=0\)
- Jibu
-
\(x=3, x=-5\)
Kutatua:\((y-6)(y+9)=0\)
- Jibu
-
\(y=6, y=-9\)
Kwa kawaida tutafanya kazi kidogo zaidi kuliko tulivyofanya katika mfano huu wa mwisho ili kutatua equations linear kwamba matokeo kutokana na kutumia Zero Bidhaa Mali.
Kutatua:\((5 n-2)(6 n-1)=0\)
- Jibu
-
\((5 n-2)(6 n-1)=0\) Tumia mali ya Bidhaa ya Zero ili kuweka
kila sababu kwa 0.\(5 n-2=0 \)
\(6 n-1=0\) Tatua equations. \(n=\frac{2}{5}\) \(n = \frac{1}{6}\) Angalia majibu yako. 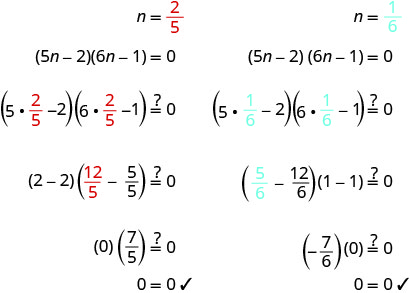
Kutatua:\((3 m-2)(2 m+1)=0\)
- Jibu
-
\(m=\frac{2}{3}, m=-\frac{1}{2}\)
Kutatua:\((4 p+3)(4 p-3)=0\)
- Jibu
-
\(p=-\frac{3}{4}, p=\frac{3}{4}\)
Angalia wakati sisi checked ufumbuzi kwamba kila mmoja wao alifanya jambo moja tu sawa na sifuri. Lakini bidhaa ilikuwa sifuri kwa ufumbuzi wote.
Kutatua:\(3 p(10 p+7)=0\)
- Jibu
-
\(3p(10p+7)=0\) Tumia mali ya Bidhaa ya Zero ili kuweka
kila sababu kwa 0.3p=0 10p+7=0 Tatua equations. p=0 10p=-7 \(p=-\frac{7}{10}\) Angalia majibu yako. 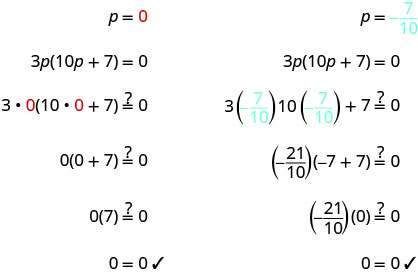
Kutatua:\(2 u(5 u-1)=0\)
- Jibu
-
\(u=0, u=\frac{1}{5}\)
Kutatua:\(w(2 w+3)=0\)
- Jibu
-
\(w=0, w=-\frac{3}{2}\)
Inaweza kuonekana kwamba kuna sababu moja tu katika mfano unaofuata. Kumbuka, hata hivyo, hiyo\((y-8)^{2}\) ina maana\((y-8)(y-8)\).
Kutatua:\((y-8)^{2}=0\)
- Jibu
-
\((y−8)^{2}=0\) Andika upya upande wa kushoto kama bidhaa. (y-8) (y-8) =0 Tumia Zero Bidhaa Mali na
kuweka kila sababu kwa 0.y-8=0 y-8=0 Tatua equations. y=8 y=8 Wakati suluhisho linarudia,
tunaiita mizizi mara mbili.Angalia jibu lako. 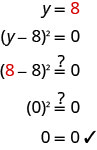
Kutatua:\((x+1)^{2}=0\)
- Jibu
-
\(x=1\)
Kutatua:\((v-2)^{2}=0\)
- Jibu
-
\(v=2\)
Tatua Ulinganisho wa Quadratic kwa kuzingatia
Kila moja ya milinganyo tuna kutatuliwa katika sehemu hii hadi sasa alikuwa upande mmoja katika fomu factored. Ili kutumia mali ya Bidhaa ya Zero, equation ya quadratic lazima ifanyike, na sifuri upande mmoja. Hivyo sisi kuwa na uhakika wa kuanza na equation quadratic katika hali ya kiwango,\(a x^{2}+b x+c=0\). Kisha tunaelezea maneno upande wa kushoto.
Kutatua:\(x^{2}+2 x-8=0\)
- Jibu
-

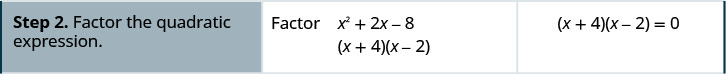



Kutatua:\(x^{2}-x-12=0\)
- Jibu
-
\(x=4, x=-3\)
Kutatua:\(b^{2}+9 b+14=0\)
- Jibu
-
\(b=-2, b=-7\)
- Andika equation quadratic katika fomu ya kawaida,\(a x^{2}+b x+c=0\).
- Fanya kujieleza kwa quadratic.
- Tumia mali ya Bidhaa ya Zero.
- Tatua equations linear.
- Angalia.
Kabla ya sisi sababu, ni lazima kuhakikisha equation quadratic ni katika hali ya kawaida.
Kutatua:\(2 y^{2}=13 y+45\)
- Jibu
-
\(2 y^{2}=13 y+45\) Andika equation quadratic katika fomu ya kawaida. \(2 y^{2}-13 y-45=0\) Fanya kujieleza kwa quadratic. \((2 y+5)(y-9)=0\) Tumia mali ya Bidhaa ya Zero
ili kuweka kila sababu kwa 0.\(2 y+5=0\) \(y-9=0\) Kutatua kila equation. \(y=-\frac{5}{2}\) \(y=9\) Angalia majibu yako. 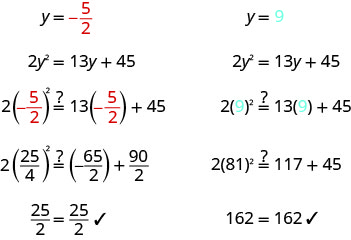
Kutatua:\(3 c^{2}=10 c-8\)
- Jibu
-
\(c=0, c=\frac{4}{3}\)
Kutatua:\(2 d^{2}-5 d=3\)
- Jibu
-
\(d=3, d=-\frac{1}{2}\)
Kutatua:\(5 x^{2}-13 x=7 x\)
- Jibu
-
\(5 x^{2}-13 x=7 x\) Andika equation quadratic katika fomu ya kawaida. \(5 x^{2}-20 x=0\) Factor upande wa kushoto wa equation. \(5 x(x-4)=0\) Tumia mali ya Bidhaa ya Zero
ili kuweka kila sababu kwa 0.\(5x=0\) \(x−4=0\) Kutatua kila equation. \(x=0\) \(x=4\) Angalia majibu yako. 
Kutatua:\(6 a^{2}+9 a=3 a\)
- Jibu
-
\(a=0, a=-1\)
Kutatua:\(45 b^{2}-2 b=-17 b\)
- Jibu
-
\(b=0, b=-\frac{1}{3}\)
Kutatua equations quadratic kwa factoring itatumia mbinu zote factoring umejifunza katika sura hii! Je, unatambua muundo maalum wa bidhaa katika mfano unaofuata?
Kutatua:\(144 q^{2}=25\)
- Jibu
-
\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)
Kutatua:\(25 p^{2}=49\)
- Jibu
-
\(p=\frac{7}{5}, p=-\frac{7}{5}\)
Kutatua:\(36 x^{2}=121\)
- Jibu
-
\(x=\frac{11}{6}, x=-\frac{11}{6}\)
Upande wa kushoto katika mfano unaofuata unafanywa, lakini upande wa kulia sio sifuri. Ili kutumia mali ya Bidhaa ya Zero, upande mmoja wa equation lazima iwe sifuri. Tutaweza kuzidisha sababu na kisha kuandika equation katika hali ya kiwango.
Kutatua:\((3 x-8)(x-1)=3 x\)
- Jibu
-
\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)
Kutatua:\((2 m+1)(m+3)=12 m\)
- Jibu
-
\(m=1, m=\frac{3}{2}\)
Kutatua:\((k+1)(k-1)=8\)
- Jibu
-
\(k=3, k=-3\)
Mali ya Bidhaa ya Zero pia inatumika kwa bidhaa ya mambo matatu au zaidi. Ikiwa bidhaa ni sifuri, angalau moja ya mambo lazima iwe sifuri. Tunaweza kutatua equations baadhi ya shahada zaidi ya mbili kwa kutumia Zero Bidhaa Mali, kama sisi kutatuliwa equations quadratic.
Kutatua:\(9 m^{3}+100 m=60 m^{2}\)
- Jibu
-
\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Kutatua:\(8 x^{3}=24 x^{2}-18 x\)
- Jibu
-
\(x=0, x=\frac{3}{2}\)
Kutatua:\(16 y^{2}=32 y^{3}+2 y\)
- Jibu
-
\(y=0, y=\frac{1}{4}\)
Wakati sisi sababu equation quadratic katika mfano unaofuata tutapata mambo matatu. Hata hivyo, sababu ya kwanza ni mara kwa mara. Tunajua kwamba sababu haiwezi sawa 0.
Kutatua:\(4 x^{2}=16 x+84\)
- Jibu
-
\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Kutatua:\(18 a^{2}-30=-33 a\)
- Jibu
-
\(a=-\frac{5}{2}, a=\frac{2}{3}\)
Kutatua:\(123 b=-6-60 b^{2}\)
- Jibu
-
\(b=2, b=\frac{1}{20}\)
Kutatua Maombi yanayotokana na equations Quadratic
Mkakati wa kutatua tatizo tulitumia mapema kwa ajili ya maombi ambayo hutafsiri kwa equations linear itafanya kazi vizuri kwa ajili ya maombi ambayo kutafsiri kwa equations quadratic. Sisi nakala ya kutatua tatizo mkakati hapa ili tuweze kuitumia kwa ajili ya kumbukumbu.
- Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
- Tambua kile tunachotafuta.
- Jina kile tunachotafuta. Chagua variable kuwakilisha kiasi hicho.
- Tafsiri katika equation. Inaweza kuwa na manufaa kurejesha tatizo katika sentensi moja na taarifa zote muhimu. Kisha, tafsiri sentensi ya Kiingereza kwenye equation ya algebra.
- Kutatua equation kutumia mbinu nzuri algebra.
- Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
- Jibu swali kwa sentensi kamili.
Tutaanza na tatizo namba kupata mazoezi kutafsiri maneno katika equation quadratic.
Bidhaa ya integers mbili mfululizo ni\(132 .\) Kupata integers.
- Jibu
-
\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)
Bidhaa ya integers mbili mfululizo ni\(240 .\) Kupata integers.
- Jibu
-
\(-15,-16\)na\(15,16\)
Bidhaa ya integers mbili mfululizo ni\(420 .\) Kupata integers.
- Jibu
-
\(-21,-20\)na\(20,21\)
Je, ulishangaa na jozi ya integers hasi ambayo ni moja ya ufumbuzi wa mfano uliopita? Bidhaa ya integers mbili nzuri na bidhaa za integers mbili hasi zote mbili hutoa 132.
Katika baadhi ya programu, ufumbuzi hasi utatokana na algebra, lakini haitakuwa kweli kwa hali hiyo.
Bustani ya mstatili ina eneo la miguu ya mraba 15. Urefu wa bustani ni miguu miwili zaidi ya upana. Pata urefu na upana wa bustani.
- Jibu
-
Hatua ya 1. Soma tatizo. Katika matatizo yanayohusisha takwimu za kijiometri, mchoro unaweza kukusaidia kutazama hali hiyo. 
Hatua ya 2. Tambua unachotafuta. Tunatafuta urefu na upana. Hatua ya 3. Jina unachotafuta.
Urefu ni miguu miwili zaidi ya upana.Hebu W = upana wa bustani.
W + 2 = urefu wa bustaniHatua ya 4. Tafsiri katika equation.
Rejesha habari muhimu katika sentensi.
Eneo la bustani ya mstatili ni futi za mraba 15.Tumia formula kwa eneo la mstatili. \(A=L \cdot W\) Mbadala katika vigezo. \(15=(W+2) W\) Hatua ya 5. Kutatua equation. Kusambaza kwanza. \(15=W^{2}+2 W\) Pata sifuri upande mmoja. \(0=W^{2}+2 W-15\) Sababu ya trinomial. \(0=(W+5)(W-3)\) Tumia mali ya Bidhaa ya Zero. \(0=W+5\) \(0=W−3\) Kutatua kila equation. \(−5=W\) \(3=W\) Kwa kuwa W ni upana wa bustani,
haina maana kwa kuwa
hasi. Tunaondoa thamani hiyo kwa W.\(W=−5\) cannot be the width, since it's negative.
\(W=3\)\(3=W\)
Upana ni miguu 3.Pata thamani ya urefu. \(\text{length}=W+2\) \(\text{length}=3+2\) \(\text{length}=5\) Urefu ni miguu 5. Hatua ya 6. Angalia jibu.
Je! Jibu lina maana?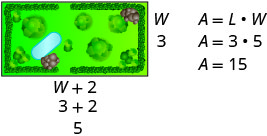
Ndiyo, hii ina maana. Hatua ya 7. Jibu swali. Upana wa bustani ni futi 3
na urefu ni futi 5.
Ishara ya mstatili ina eneo la miguu ya mraba 30. Urefu wa ishara ni mguu mmoja zaidi ya upana. Pata urefu na upana wa ishara.
- Jibu
-
Miguu 55 na miguu 66
Patio ya mstatili ina eneo la futi za mraba 180. Upana wa patio ni miguu mitatu chini ya urefu. Pata urefu na upana wa patio.
- Jibu
-
Miguu 12 na miguu 15
Katika sura ya awali, tulitumia Theorem ya Pythagorean\(\left(a^{2}+b^{2}=c^{2}\right)\). Ilitoa uhusiano kati ya miguu na hypotenuse ya pembetatu sahihi.
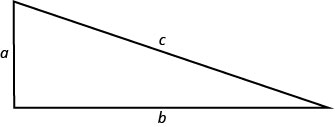
Tutatumia formula hii kwa mfano unaofuata.
Justine anataka kuweka staha katika kona ya mashamba yake katika sura ya pembetatu ya kulia, kama inavyoonekana hapa chini. Hypotenuse itakuwa urefu wa miguu 17. Urefu wa upande mmoja utakuwa chini ya miguu 7 kuliko urefu wa upande mwingine. Pata urefu wa pande za staha.
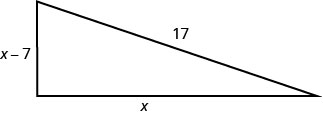
- Jibu
-
Hatua ya 1. Soma tatizo. Hatua ya 2. Tambua unachotafuta. Tunatafuta urefu wa pande
za staha.Hatua ya 3. Jina unachotafuta.
Upande mmoja ni 7 chini ya nyingine.Hebu x = urefu wa upande wa staha
x - 7 = urefu wa upande mwingineHatua ya 4. Tafsiri katika equation.
Kwa kuwa hii ni pembetatu sahihi tunaweza kutumia Theorem ya
Pythagorean.\(a^{2}+b^{2}=c^{2}\) Mbadala katika vigezo. \(x^{2}+(x-7)^{2}=17^{2}\) Hatua ya 5. Kutatua equation. \(x^{2}+x^{2}-14 x+49=289\) Kurahisisha. \(2 x^{2}-14 x+49=289\) Ni equation quadratic, hivyo kupata sifuri upande mmoja. \(2 x^{2}-14 x-240=0\) Factor sababu kubwa ya kawaida. \(2\left(x^{2}-7 x-120\right)=0\) Sababu ya trinomial. \(2(x-15)(x+8)=0\) Tumia mali ya Bidhaa ya Zero. \(2\neq 0\) \(x−15=0\) \(x+8=0\) Kutatua. \(2\neq 0\) \(x=15\) \(x=-8\) Kwa kuwa\(x\) ni upande wa pembetatu,\(x=−8\) haina
maana.\(2\neq 0\) \(x=15\) \(\cancel{x=−8}\) Pata urefu wa upande mwingine. Ikiwa urefu wa upande mmoja ni \(x=15\) basi urefu wa upande mwingine ni \(x-7\) \(15 - 7 = 8\) 8 ni urefu wa upande mwingine. Hatua ya 6. Angalia jibu.
Je, nambari hizi zina maana?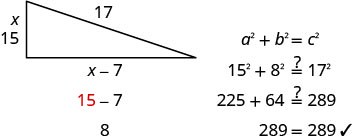
Hatua ya 7. Jibu swali. Pande za staha ni 8, 15, na 17 miguu.
Meli ya mashua ni pembetatu sahihi. Urefu wa upande mmoja wa meli ni futi 7 zaidi ya upande mwingine. Hypotenuse ni 13. Pata urefu wa pande mbili za meli.
- Jibu
-
Miguu 5 na miguu 12
Bustani ya kutafakari iko katika sura ya pembetatu ya kulia, na mguu mmoja wa miguu 7. Urefu wa hypotenuse ni moja zaidi ya urefu wa moja ya miguu mingine. Pata urefu wa hypotenuse na mguu mwingine.
- Jibu
-
Miguu 24 na miguu 25
Dhana muhimu
- Zero Bidhaa Mali Kama\(a \cdot b=0\), basi aidha a=0 au b = 0 au wote wawili. Angalia Mfano.
- Kutatua equation quadratic kwa factoring Ili kutatua equation quadratic kwa factoring: Angalia Mfano.
- Andika equation quadratic katika fomu ya kawaida,\(a x^{2}+b x+c=0\).
- Fanya kujieleza kwa quadratic.
- Tumia mali ya Bidhaa ya Zero.
- Tatua equations linear.
- Angalia.
- Tumia mkakati wa kutatua tatizo kutatua matatizo ya neno Angalia Mfano.
- Soma tatizo. Hakikisha maneno yote na mawazo yanaeleweka.
- Tambua kile tunachotafuta.
- Jina kile tunachotafuta. Chagua variable kuwakilisha kiasi hicho.
- Tafsiri katika equation. Inaweza kuwa na manufaa kurejesha tatizo katika sentensi moja na taarifa zote muhimu. Kisha, tafsiri sentensi ya Kiingereza kwenye equation ya algebra.
- Kutatua equation kutumia mbinu nzuri algebra.
- Angalia jibu katika tatizo na uhakikishe kuwa ni busara.
- Jibu swali kwa sentensi kamili.
faharasa
- equations quadratic
- ni equations ambayo variable ni squared.
- Zero Bidhaa Mali
- Mali ya Bidhaa ya Zero inasema kwamba, ikiwa bidhaa ya kiasi mbili ni sifuri, angalau moja ya kiasi ni sifuri.


