Skip to main content
Global

7.3: Vipengele vya Quadratic vya Quadratic na Mgawo wa Uongozi Zaidi ya 1

  1. Last updated
  2. Save as PDF
  • Page ID
    177493

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Kutambua mkakati wa awali kwa sababu polynomials kabisa
    • Factor trinomials ya fomu\(ax^{2}+bx+c\) na GCF
    • Vipengele vya trinomials kutumia jaribio na hitilafu
    • Vipengele vya trinomials kutumia njia ya 'ac'
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kupata GCF ya 45\(p^{2}\) na 30\(p^{6}\)
      Kama amekosa tatizo hili, mapitio Zoezi 7.1.4.
    2. Kuzidisha\((3 y+4)(2 y+5)\)
      Ikiwa umekosa tatizo hili, tathmini Zoezi 6.3.37.
    3. Kuchanganya kama maneno\(12 x^{2}+3 x+5 x+9\)
      Kama amekosa tatizo hili, mapitio Zoezi 1.3.37.

    Kutambua Mkakati wa awali wa Kufanya

    Hebu muhtasari ambapo sisi ni hadi sasa na factoring polynomials. Katika sehemu mbili za kwanza za sura hii, tulitumia mbinu tatu za kuzingatia: kuzingatia GCF, kuzingatia kwa makundi, na kuzingatia trinomial kwa “kufuta” FOIL. Mbinu zaidi zitafuata unapoendelea katika sura hii, na baadaye katika masomo yako ya algebra.

    Je, utajuaje wakati wa kutumia kila njia ya factoring? Unapojifunza mbinu zaidi za kuzingatia, utajuaje wakati wa kutumia kila njia na usiwachanganyike? Itasaidia kuandaa mbinu za factoring katika mkakati ambao unaweza kukuongoza kutumia njia sahihi.

    Unapoanza kuzingatia polynomial, daima uulize kwanza, “Je, kuna sababu kubwa ya kawaida?” Ikiwa kuna, fikiria kwanza.

    Kitu kingine cha kuzingatia ni aina ya polynomial. Je, ni maneno ngapi? Je, ni binomial? Trinomial? Au ina maneno zaidi ya tatu?

    • Ikiwa ni trinomial ambapo mgawo wa kuongoza ni moja\(x^{2}+b x+c\), tumia njia ya “kufuta FOIL”.
    • Ikiwa ina maneno zaidi ya tatu, jaribu njia ya kikundi. Hii ndiyo njia pekee ya kutumia kwa polynomials ya maneno zaidi ya tatu.

    Baadhi ya polynomials haiwezi kufananishwa. Wanaitwa “mkuu.” Chini sisi muhtasari mbinu tuna hadi sasa.

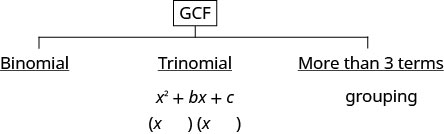
    Takwimu hii inaorodhesha mikakati ya factoring polynomials. Juu ya takwimu ni G C F, ambapo factoring daima huanza. Kutoka huko, takwimu ina matawi matatu. Ya kwanza ni binomial, ya pili ni trinomial na fomu x ^ 2 + b x +c, na ya tatu ni “maneno zaidi ya tatu”, ambayo inaitwa na kikundi.

    CHAGUA MKAKATI WA SABABU POLYNOMIALS KABISA.
    1. Je, kuna sababu kubwa ya kawaida?
      • Factor ni nje.
    2. Je, polynomial ni binomial, trinomial, au kuna maneno zaidi ya tatu?
      • Ikiwa ni binomial, hivi sasa hatuna njia ya kuzingatia.
      • Ikiwa ni trinomial ya fomu\(x^{2}+b x+c\): Tengeneza FOIL\((x\qquad)(x\qquad)\)
      • Ikiwa ina maneno zaidi ya tatu: Tumia njia ya kikundi.
    3. Angalia kwa kuzidisha mambo.

    Tumia mkakati wa awali kwa sababu ya polynomial kabisa. Polynomial inachukuliwa kabisa ikiwa, isipokuwa monomials, mambo yake yote ni ya kwanza.

    Zoezi\(\PageIndex{1}\)

    Tambua njia bora ya kutumia ili kuzingatia kila polynomial.

    1. \(6 y^{2}-72\)
    2. \(r^{2}-10 r-24\)
    3. \(p^{2}+5 p+p q+5 q\)
    Jibu

    \[\begin{array}{ll} &6 y^{2}-72\\ \text { Is there a greatest common factor? } & \text {Yes, 6. } \\ \text { Factor out the } 6 &6\left(y^{2}-12\right) \\ \text { Is it a binomial, trinomial, or are there } & \text {Binomial, we have no method to factor } \\ \text { more than } 3 \text { terms? } & \text {binomials yet. } \end{array} \nonumber\]

    Jibu b

    \[\begin{array}{ll} &r^{2}-10 r-24\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {Trinomial, with leading coefficient } 1, \text { so } \\ \text { more than three terms? }& \text {"undo" FOIL. }\end{array} \nonumber\]

    Jibu c

    \[\begin{array}{ll} &p^{2}+5 p+p q+5 q\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {More than three terms, so factor using }\\ \text { more than three terms? }& \text {grouping. }\end{array} \nonumber\]

    Zoezi\(\PageIndex{2}\)

    Tambua njia bora ya kutumia ili kuzingatia kila polynomial:

    1. \(4 y^{2}+32\)
    2. \(y^{2}+10 y+21\)
    3. \(y z+2 y+3 z+6\)
    Jibu

    hakuna njia

    Jibu b

    tengua kutumia FOIL

    Jibu c

    sababu na kikundi

    Zoezi\(\PageIndex{3}\)

    Tambua njia bora ya kutumia ili kuzingatia kila polynomial:

    1. \(a b+a+4 b+4\)
    2. \(3 k^{2}+15\)
    3. \(p^{2}+9 p+8\)
    Jibu

    sababu kwa kutumia kikundi

    Jibu b

    hakuna njia

    Jibu c

    tengua kutumia FOIL

    Factor Trinomials ya fomu shaba 2 + bx + c na GCF

    Sasa kwa kuwa tumeandaa kile tulichofunikwa hadi sasa, tuko tayari kuzingatia trinomials ambao mgawo wa kuongoza sio 1, trinomials ya fomu\(a x^{2}+b x+c\). Kumbuka daima kuangalia kwa GCF kwanza! Wakati mwingine, baada ya kuzingatia GCF, mgawo wa kuongoza wa trinomial unakuwa 1 na unaweza kuifanya kwa njia katika sehemu ya mwisho. Hebu tufanye mifano michache ili kuona jinsi hii inavyofanya kazi. Jihadharini na ishara katika mifano miwili ijayo.

    Zoezi\(\PageIndex{4}\)

    Sababu kabisa:\(2 n^{2}-8 n-42\).

    Jibu

    Tumia mkakati wa awali.

    \(\begin{array}{ll} \text { Is there a greatest common factor? }&2 n^{2}-8 n-42\\ \text { Yes, GCF }=2 . \text { Factor it out. }& 2\left(n^{2}-4 n-21\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 2(n\qquad )(n\qquad) \\ \text { Use } 3 \text { and }-7 \text { as the last terms of the binomials. } & 2(n+3)(n-7) \end{array}\)

    Mambo ya -21 Jumla ya mambo
    1, -21 1+ (-21) =-20
    3, -7 3+ (-7) =-4*

    \(\begin{array}{l}{\text {Check. }} \\ {2(n+3)(n-7)} \\ {2\left(n^{2}-7 n+3 n-21\right)} \\ {2\left(n^{2}-4 n-21\right)} \\ {2 n^{2}-8 n-42 }\checkmark \end{array}\)

    Zoezi\(\PageIndex{5}\)

    Sababu kabisa:\(4 m^{2}-4 m-8\)

    Jibu

    4\((m+1)(m-2)\)

    Zoezi\(\PageIndex{6}\)

    Sababu kabisa:\(5 k^{2}-15 k-50\)

    Jibu

    5\((k+2)(k-5)\)

    Zoezi\(\PageIndex{7}\)

    Sababu kabisa:\(4 y^{2}-36 y+56\)

    Jibu

    Tumia mkakati wa awali.
    \(\begin{array}{ll} \text { Is there a greatest common factor? }&4 y^{2}-36 y+56\\ \text { Yes, GCF }=4 . \text { Factor it out. }&4\left(y^{2}-9 y+14\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 4(y\qquad )(y\qquad) \\\text { Use a table like the one below to find two numbers that multiply to }&\\ 14 \text { and add to }-9\\ \text { Both factors of } 14 \text { must be negative. } & 4(y-2)(y-7) \end{array}\)

    Mambo ya 14 Jumla ya mambo
    -1, -14 -1+ (-14) =-15
    -2, -7 -2+ (-7) =-9*

    \(\begin{array}{l}{\text { Check. }} \\ {4(y-2)(y-7)} \\ {4\left(y^{2}-7 y-2 y+14\right)} \\ {4\left(y^{2}-9 y+14\right)} \\ {4 y^{2}-36 y+42 } \checkmark \end{array}\)

    Zoezi\(\PageIndex{8}\)

    Sababu kabisa:\(3 r^{2}-9 r+6\)

    Jibu

    3\((r-1)(r-2)\)

    Zoezi\(\PageIndex{9}\)

    Sababu kabisa:\(2 t^{2}-10 t+12\)

    Jibu

    2\((t-2)(t-3)\)

    Katika mfano unaofuata GCF itajumuisha kutofautiana.

    Zoezi\(\PageIndex{10}\)

    Sababu kabisa:\(4 u^{3}+16 u^{2}-20 u\)

    Jibu

    Tumia mkakati wa awali.
    \(\begin{array}{ll} \text { Is there a greatest common factor? }&4 u^{3}+16 u^{2}-20 u\\ \text { Yes, GCF }=4 u . \text { Factor it. }&4 u\left(u^{2}+4 u-5\right) \\\text { Binomial, trinomial, or more than three terms? }&\\ \text { more than three terms? }& \\ \text { It is a trinomial. So "undo FOIL." } & 4u(u\qquad )(u\qquad) \\\text { Use a table like the table below to find two numbers that }&4 u(u-1)(u+5)\\ \text { multiply to }-5 \text { and add to } 4\end{array}\)

    Mambo ya -5 Jumla ya mambo
    —1,5 -1+5=4*
    1, -5 1+ (-5) =-4

    Angalia.

    \(\begin{array}{l}{4 u(u-1)(u+5)} \\ {4 u\left(u^{2}+5 u-u-5\right)} \\ {4 u\left(u^{2}+4 u-5\right)} \\ {4 u^{3}+16 u^{2}-20 u }\checkmark \end{array}\)

    Zoezi\(\PageIndex{11}\)

    Sababu kabisa:\(5 x^{3}+15 x^{2}-20 x\)

    Jibu

    5\(x(x-1)(x+4)\)

    Zoezi\(\PageIndex{12}\)

    Sababu kabisa:\(6 y^{3}+18 y^{2}-60 y\)

    Jibu

    6\(y(y-2)(y+5)\)

    Factor Trinomials kutumia Jaribio na Hitilafu

    Ni nini kinachotokea wakati mgawo wa kuongoza sio 1 na hakuna GCF? Kuna mbinu kadhaa ambazo zinaweza kutumiwa kuzingatia hizi trinomials. Kwanza tutatumia njia ya Jaribio na Hitilafu.

    Hebu tuchunguze trinomial\(3 x^{2}+5 x+2\)

    Kutoka kwa kazi yetu ya awali tunatarajia hii itafanyika katika binomials mbili.

    \[\begin{array}{c}{3 x^{2}+5 x+2} \\ {( \qquad)( \qquad)}\end{array}\]

    Tunajua maneno ya kwanza ya mambo ya binomial yatazidisha kutupa 3\(x^{2}\). Sababu pekee za 3\(x^{2}\) ni\(1 x, 3 x\). Tunaweza kuwaweka katika binomials.

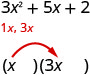
    Takwimu hii ina polynomial 3 x^ 2 +5 x +2. Chini kuna maneno mawili, 1 x, na 3 x Chini hizi ni sababu mbili x na (3 x) kuwa umeonyesha kuzidisha.

    Angalia. Je,\(1 x \cdot 3 x=3 x^{2}\)?

    Tunajua masharti ya mwisho ya binomials yatazidisha hadi 2. Kwa kuwa hii trinomial ina maneno yote mazuri, tunahitaji tu kuzingatia mambo mazuri. Sababu pekee za 2 ni 1 na 2. Lakini sasa tuna kesi mbili ya kuzingatia kama itakuwa kuleta tofauti kama sisi kuandika 1, 2, au 2, 1.

    Takwimu hii inaonyesha sababu zinazowezekana za 3x ^ 2 +5x +2 ya polynomial. Polynomial imeandikwa mara mbili. Chini ya wote wawili, kuna maneno 1x, 3x chini ya 3x ^ 2. Pia, kuna sababu 1,2 chini ya muda wa 2. Chini ya takwimu kuna factorizations mbili iwezekanavyo ya polynomial. Ya kwanza ni (x + 1) (3x + 2) na inayofuata ni (x + 2) (3x + 1).

    Ni mambo gani sahihi? Kuamua kwamba, tunazidisha maneno ya ndani na nje.

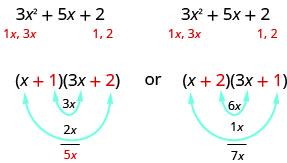
    Takwimu hii inaonyesha sababu zinazowezekana za polynomial 3 x^ 2 + 5 x +2. Polynomial imeandikwa mara mbili. Chini ya wote wawili, kuna maneno 1 x, 3 x chini ya 3 x ^ 2. Pia, kuna sababu 1, 2 chini ya muda wa 2. Chini ya takwimu kuna factorizations mbili iwezekanavyo ya polynomial. Ya kwanza ni (x + 1) (3 x + 2). Chini ya factorization hii ni bidhaa 3 x kutoka kuzidisha maneno ya kati 1 na 3 x Pia kuna bidhaa ya 2 x kutoka kuzidisha maneno ya nje x na 2. Bidhaa hizi za 3 x na 2 x zinaongeza 5 x Chini ya factorization ya pili ni bidhaa 6 x kutoka kuzidisha maneno ya kati 2 na 3 x Pia kuna bidhaa ya 1 x kutoka kuzidisha maneno ya nje x na 1. Bidhaa hizi mbili za 6 x na 1 x kuongeza 7 x.

    Tangu muda wa kati wa trinomial ni 5 x, sababu katika kesi ya kwanza itafanya kazi. Hebu FOIL kuangalia.

    \[\begin{array}{l}{(x+1)(3 x+2)} \\ {3 x^{2}+2 x+3 x+2} \\ {3 x^{2}+5 x+2}\checkmark \end{array}\]

    Matokeo yetu ya factoring ni:

    \[\begin{array}{l}{3 x^{2}+5 x+2} \\ {(x+1)(3 x+2)}\end{array}\]

    Zoezi\(\PageIndex{13}\): How to Factor Trinomials of the Form \(ax^2+bx+c\) Using Trial and Error

    Sababu kabisa:\(3 y^{2}+22 y+7\)

    Jibu

    Jedwali hili linafupisha hatua za kuzingatia 3 y ^ 2 + 22 y + 7. Mstari wa kwanza unasema kuandika trinomial katika utaratibu wa kushuka. Polynomial imeandikwa 3 y ^ 2 +22 y + 7.Mstari wa pili inasema kupata jozi zote za muda wa kwanza. Jozi pekee zilizoorodheshwa ni 1 y, 3 y.Kisha, kwa kuwa kuna jozi moja tu, ziko katika mabano yaliyoandikwa (1 y) na (3 y).Mstari wa tatu unasema “tafuta jozi zote zilizowekwa kwa muda wa tatu”. Pia inasema mambo pekee ya 7 ni 1 na 7.Mstari wa nne unasema mtihani mchanganyiko wote unaowezekana wa mambo mpaka bidhaa sahihi inapatikana. Sababu zinazowezekana zinaonyeshwa (y + 1) (3 y + 7) na (y + 7) (3y + 1). Chini ya kila sababu ni bidhaa za maneno ya nje na maneno ya ndani. Kwa kwanza ni 7y na 3y. Kwa pili ni 21 y na y. mchanganyiko (y + 7) (3 y + 1) ni factoring sahihi.

    Mstari wa mwisho unasema kuangalia kwa kuzidisha. Bidhaa ya (y + 7) (3 y + 1) inavyoonyeshwa kama 3 y ^ 2 + 22 y + 7.
    Zoezi\(\PageIndex{14}\)

    Sababu kabisa:\(2 a^{2}+5 a+3\)

    Jibu

    \((a+1)(2 a+3)\)

    Zoezi\(\PageIndex{15}\)

    Sababu kabisa:\(4 b^{2}+5 b+1\)

    Jibu

    \((b+1)(4 b+1)\)

    VIPENGELE VYA TRINOMIALS YA FOMU\(ax^2+bx+c\) USING TRIAL AND ERROR.
    1. Andika trinomial katika utaratibu wa kushuka kwa digrii.
    2. Pata jozi zote za muda wa kwanza.
    3. Pata jozi zote za muda wa tatu.
    4. Jaribu mchanganyiko wote unaowezekana wa mambo mpaka bidhaa sahihi inapatikana.
    5. Angalia kwa kuzidisha.

    Wakati muda wa kati ni hasi na muda wa mwisho ni chanya, ishara katika binomials lazima zote ziwe hasi.

    Zoezi\(\PageIndex{16}\)

    Sababu kabisa:\(6 b^{2}-13 b+5\)

    Jibu
    The trinomial tayari iko katika utaratibu wa kushuka. .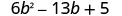
    Pata sababu za muda wa kwanza. .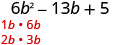
    Pata sababu za muda wa mwisho. Fikiria ishara. Tangu muda wa mwisho, 5 ni chanya, sababu zake lazima ziwe chanya au zote mbili ziwe hasi. Mgawo wa muda wa kati ni hasi, kwa hiyo tunatumia sababu hasi. .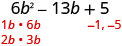
    Fikiria mchanganyiko wote wa mambo.
    \(6 b^{2}-13 b+5\)
    Sababu zinazowezekana Bidhaa
    \ (6 b^ {2} -13 b+5\) Sababu zinazowezekana” data-valign="top” class="lt-math-15168"> (b-1) (6b-5) \ (6 b^ {2} -13 b+5\) Bidhaa” data-valign="top” class="lt-math-15168">\(6 b^{2}-11 b+5\)
    \ (6 b^ {2} -13 b+5\) Sababu zinazowezekana” data-valign="top” class="lt-math-15168"> (b-5) (6b-1) \ (6 b^ {2} -13 b+5\) Bidhaa” data-valign="top” class="lt-math-15168">\(6 b^{2}-31 b+5\)
    \ (6 b^ {2} -13 b+5\) Sababu zinazowezekana” data-valign="top” class="lt-math-15168"> (2b-1) (3b-185) \ (6 b^ {2} -13 b+5\) Bidhaa” data-valign="top” class="lt-math-15168">\(6 b^{2}-13 b+5\) *
    \ (6 b^ {2} -13 b+5\) Sababu zinazowezekana” data-valign="top” class="lt-math-15168"> (2b-5) (3b-1) \ (6 b^ {2} -13 b+5\) Bidhaa” data-valign="top” class="lt-math-15168">\(6 b^{2}-17 b+5\)
    \(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 b-1)(3 b-5)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 v}\checkmark \end{array}\end{array}\)
    Zoezi\(\PageIndex{17}\)

    Sababu kabisa:\(8 x^{2}-14 x+3\)

    Jibu

    \((2 x-3)(4 x-1)\)

    Zoezi\(\PageIndex{18}\)

    Sababu kabisa:\(10 y^{2}-37 y+7\)

    Jibu

    \((2 y-7)(5 y-1)\)

    Wakati sisi sababu kujieleza, sisi daima kuangalia kwa sababu kubwa ya kawaida kwanza. Ikiwa maneno hayana sababu kubwa ya kawaida, hawezi kuwa na moja katika mambo yake ama. Hii inaweza kutusaidia kuondoa baadhi ya mchanganyiko wa sababu zinazowezekana.

    Zoezi\(\PageIndex{19}\)

    Sababu kabisa:\(14 x^{2}-47 x-7\)

    Jibu
    The trinomial tayari iko katika utaratibu wa kushuka. .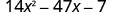
    Pata sababu za muda wa kwanza. .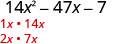
    Pata sababu za muda wa mwisho. Fikiria ishara. Kwa kuwa ni hasi, jambo moja lazima liwe chanya na moja hasi. .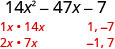
    Fikiria mchanganyiko wote wa mambo. Tunatumia kila jozi ya mambo ya 14\(x^{2}\) na kila jozi ya mambo ya -7.
    Mambo ya\(14x^2\) Jozi na Mambo ya -7
    \ (14x^2\)” data-valign="top” class="lt-math-15168">\(x, 14 x\)   11, -7
    -7, 11
    (utaratibu wa reverse)
    \ (14x^2\)” data-valign="top” class="lt-math-15168">\(x, 14 x\)   -1, 77
    77, -1
    (utaratibu wa reverse)
    \ (14x^2\)” data-valign="top” class="lt-math-15168">\(2x,7x\)   11, -7
    -7, 11
    (utaratibu wa reverse)
    \ (14x^2\)” data-valign="top” class="lt-math-15168">\(2x,7x\)   -1, 77
    77, -1
    (utaratibu wa reverse)

    Jozi hizi husababisha mchanganyiko nane wafuatayo.

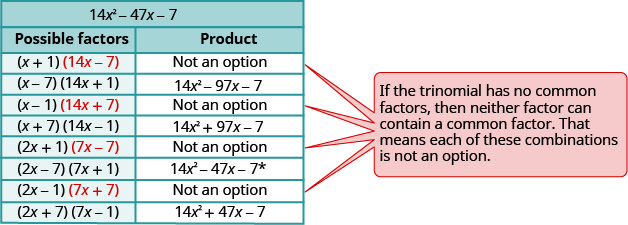
    Jedwali hili lina kichwa cha 14 x ^ 2 - 47 x bala 7. Jedwali hili lina nguzo mbili. Safu ya kwanza inaitwa “sababu zinazowezekana” na safu ya pili inaitwa “bidhaa”. Safu ya kwanza inaorodhesha mchanganyiko wote wa mambo iwezekanavyo na safu ya pili ina bidhaa. Katika mstari wa kwanza chini ya “sababu zinazowezekana” inasoma (x+1) na (14 x minus 7). Chini ya bidhaa, katika safu inayofuata, inasema “si chaguo”. Katika mstari unaofuata chini, inaonyesha (x minus 7) na (14 x pamoja na 1). Katika mstari unaofuata chini, inaonyesha (x minus 1) na (14 x pamoja na 7). Karibu na hili katika safu ya bidhaa, inasema “si chaguo.” Mstari uliofuata chini ya “sababu zinazowezekana”, ina equation (x plus 7 na 14 x minus 1). Karibu na hili katika safu ya bidhaa ina 14 x ^2 pamoja na 97 x minus 7. Mstari uliofuata chini ya sababu zinazowezekana, ina 2 x pamoja na 1 na 7 x minus 7. Karibu na hii chini ya safu ya bidhaa, inasema “si chaguo”. Mstari uliofuata chini unasoma 2 x minus 7 na 7x pamoja na 1. Karibu na hili chini ya safu ya bidhaa, ina 14 x ^2 minus 47 x minus 7 na asterisk ifuatayo 7. Mstari uliofuata chini unasoma 2 x minus 1 na 7 x pamoja na 7. Karibu na hili katika safu ya bidhaa inasoma “si chaguo”. Mstari wa mwisho unasoma 2 x pamoja na 7 na 7 x minus 1. Karibu na hili katika safu ya bidhaa inasoma 14, x, ^ 2 pamoja na 47 x minus 7. Karibu na meza ni sanduku yenye mishale minne inayoelezea kila mstari “sio chaguo”. Sababu iliyotolewa katika sanduku la maandishi ni “ikiwa trinomial haina mambo ya kawaida, basi hakuna sababu inaweza kuwa na jambo la kawaida. Hiyo ina maana kwamba kila moja ya mchanganyiko huu si chaguo.”
    \(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 x-7)(7 x+1)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 }\checkmark \end{array}\end{array}\)
    Zoezi\(\PageIndex{20}\)

    Sababu kabisa:\(8 a^{2}-3 a-5\)

    Jibu

    \((a-1)(8 a+5)\)

    Zoezi\(\PageIndex{21}\)

    Sababu kabisa:\(6 b^{2}-b-15\)

    Jibu

    \((2 b+3)(3 b-5)\)

    Zoezi\(\PageIndex{22}\)

    Sababu kabisa:\(18 n^{2}-37 n+15\)

    Jibu
    The trinomial tayari iko katika utaratibu wa kushuka. \(18 n^{2}-37 n+15\)
    Pata sababu za muda wa kwanza. .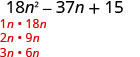
    Pata sababu za muda wa mwisho. Fikiria ishara. Kwa kuwa 15 ni chanya na mgawo wa muda wa kati ni hasi, tunatumia sababu hasi. .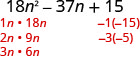

    Fikiria mchanganyiko wote wa mambo.

    Jedwali hili lina kichwa 18 n ^ 2 - 37n + 15. Jedwali hili lina nguzo mbili. Safu ya kwanza imeandikwa sababu zinazowezekana na safu ya pili imeandikwa bidhaa. Safu ya kwanza inaorodhesha mchanganyiko wote wa mambo iwezekanavyo na safu ya pili ina bidhaa. Safu nane zinaorodhesha bidhaa sio chaguo. Kuna sanduku la maandishi linalotoa sababu ya chaguo. Sababu katika sanduku la maandishi ni “ikiwa trinomial haina mambo ya kawaida, basi hakuna sababu inaweza kuwa na sababu ya kawaida”. Mstari ulio na mambo (2n - 3) (9n - 5) na bidhaa 18n ^ 2 minus 37 n + 15 ina kinyota.
    \(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 n-3)(9 n-5)\\\\\text {Check by multiplying. } \\\\ \begin{array}{l}{(2 n-3)(9 n-5)} \\ {18 n^{2}-10 n-27 n+15} \\ {18 n^{2}-37 n+15 } \checkmark\end{array} \end{array}\)
    Zoezi\(\PageIndex{23}\)

    Sababu kabisa:\(18 x^{2}-3 x-10\)

    Jibu

    \((3 x+2)(6 x-5)\)

    Zoezi\(\PageIndex{24}\)

    Sababu kabisa:\(30 y^{2}-53 y-21\)

    Jibu

    \((3 y+1)(10 y-21)\)

    Usisahau kutafuta GCF kwanza.

    Zoezi\(\PageIndex{25}\)

    Sababu kabisa:\(10 y^{4}+55 y^{3}+60 y^{2}\)

    Jibu
      \(10 y^{4}+55 y^{3}+60 y^{2}\)
    Angalia kubwa ya kawaida sababu, na sababu ni ya kwanza. 5\(y^{2}\left(2 y^{2}+11 y+12\right)\)
    Sababu ya trinomial. .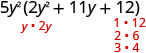

    Fikiria mchanganyiko wote.

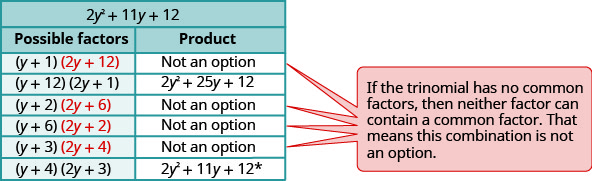
    Jedwali hili lina kichwa cha 2 y squared + 11 y + 12 Jedwali hili lina nguzo mbili. Safu ya kwanza inaitwa “sababu zinazowezekana” na safu ya pili inaitwa “bidhaa”. Safu ya kwanza inaorodhesha mchanganyiko wote wa mambo iwezekanavyo na safu ya pili ina bidhaa. Safu nne zinaorodhesha bidhaa sio chaguo. Kuna sanduku la maandishi linalotoa sababu ya chaguo. Sababu katika sanduku la maandishi ni “ikiwa trinomial haina mambo ya kawaida, basi hakuna sababu inaweza kuwa na sababu ya kawaida”. Mstari ulio na mambo (y + 4) (2y + 3) na bidhaa 2 y squared + 11 y + 12 ina asterisk.
    \(\begin{array}{ll}\text{The correct factors are those whose product} &5 y^{2}(y+4)(2 y+3) \\ \text{is the original trinomial. Remember to include} & \\\text {the factor } 5 y^{2}\\\text {Check by multiplying. } \\\\ \begin{array}{l}{5 y^{2}(y+4)(2 y+3)} \\ {5 y^{2}\left(2 y^{2}+8 y+3 y+12\right)} \\ {10 y^{4}+55 y^{3}+60 y^{2}}\checkmark\end{array} \end{array}\)
    Zoezi\(\PageIndex{26}\)

    Sababu kabisa:\(15 n^{3}-85 n^{2}+100 n\)

    Jibu

    5\(n(n-4)(3 n-5)\)

    Zoezi\(\PageIndex{27}\)

    Sababu kabisa:\(56 q^{3}+320 q^{2}-96 q\)

    Jibu

    8\(q(q+6)(7 q-2)\)

    Factor Trinomials kutumia “ac” Njia

    Njia nyingine ya kuzingatia trinomials ya fomu\(ax^2+bx+c\) ni njia ya “ac”. (Njia ya “ac” wakati mwingine huitwa njia ya makundi.) Njia ya “ac” ni kweli ugani wa mbinu ulizotumia katika sehemu ya mwisho ili kuzingatia trinomials na mgawo wa kuongoza moja. Njia hii imeundwa sana (hiyo ni hatua kwa hatua), na inafanya kazi daima!

    Zoezi\(\PageIndex{28}\): How to Factor Trinomials Using the “ac” Method

    Sababu:\(6 x^{2}+7 x+2\)

    Jibu

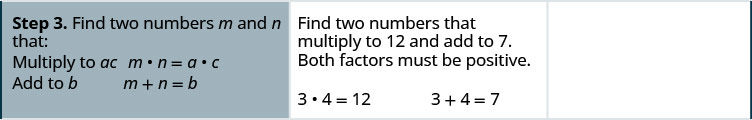
    Jedwali hili linaorodhesha hatua za kuzingatia 6 x ^ 2 + 7 x + 2. Hatua ya kwanza ni kuzingatia GCF. Polynomial hii haina.Mstari wa pili inasema kupata bidhaa c Kisha, inaorodhesha c kama mara 6 2 = 12.Hatua ya tatu ni kupata namba mbili m na n ambayo m mara n = c na m + n = b. safu ya kati inasoma, “tafuta namba mbili zinazoongeza 7. Sababu zote mbili lazima ziwe chanya”. Idadi ni 3 na 4. Mara 3 4 ni 12 na 3 + 4 ni 7.Hatua inayofuata ni kugawanya muda wa kati kwa kutumia m na n Hiyo ni, kuandika 7 x kama 3 x + 4 x Kwa hiyo, 6 x ^ 2 + 7 x 2 imeandikwa upya kama 6 x ^ 2 +3 x 4 x + 2.Hatua inayofuata ni kuzingatia kwa kikundi. 3 x (2 x + 1) + 2 (2 x + 1) kisha factor tena (2 x + 1) (3 x + 2).Hatua ya mwisho ni kuangalia kwa kuzidisha. Panua mambo (2 x + 1) (3 x + 2) ili kupata 6 x ^ 2 + 7 x + 2.

    Zoezi\(\PageIndex{29}\)

    Sababu:\(6 x^{2}+13 x+2\)

    Jibu

    \((x+2)(6 x+1)\)

    Zoezi\(\PageIndex{30}\)

    Sababu:\(4 y^{2}+8 y+3\)

    Jibu

    \((2 y+1)(2 y+3)\)

    VIPENGELE VYA TRINOMIALS YA FOMU KWA KUTUMIA NJIA YA “AC”.
    1. Sababu yoyote GCF.
    2. Pata ac ya bidhaa.
    3. Kupata namba mbili m na n kwamba:
      \(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\)
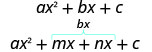
    4. Split muda wa kati kwa kutumia m na n:Takwimu hii inaonyesha equations mbili. Equation juu inasoma mara x squared pamoja b mara x plus c. chini ya hii, ni equation mara x squared pamoja m mara x plus n mara x plus c. zaidi m mara x plus n mara x x ni mabano na b mara x juu yake.
    5. Sababu kwa kikundi.
    6. Angalia kwa kuzidisha mambo.

    Wakati muda wa tatu wa trinomial ni hasi, sababu za muda wa tatu zitakuwa na ishara tofauti.

    Zoezi\(\PageIndex{31}\)

    Sababu:\(8 u^{2}-17 u-21\)

    Jibu
    Je, kuna sababu kubwa ya kawaida? Hapana.   .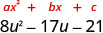
    Kupata\(a\cdot c\) \(a\cdot c\)  
      8 (-21)  
      -168

    Pata namba mbili zinazozidisha hadi -168 na uongeze hadi -17. Sababu kubwa lazima iwe hasi.

    Mambo ya -168 Jumla ya mambo
    1, -168 1+ (-168) =-167
    2,84 2+ (-84) =-82
    3, -56 3+ (-56) =-53
    4, -42 4+ (-42) =-38
    6,28 6+ (-28) =-22
    7,24 7+ (-24) =-17*
    8,21 8+ (-21) =-13

    \(\begin{array}{lc}\text { Split the middle term using } 7 u \text { and }-24 u &8 u^{2}-17 u-21 \\ & \qquad\space \swarrow\searrow \\ & \underbrace{8 u^{2}+7 u} \underbrace{-24 u-21} \\ \text { Factor by grouping. } & u(8 u+7)-3(8 u+7) \\ & (8 u+7)(u-3) \\ \text { Check by multiplying. } & \begin{array}{l}{(8 u+7)(u-3)} \\ {8 u^{2}-24 u+7 u-21} \\ {8 u^{2}-17 u-21} \checkmark \end{array} \end{array}\)

    Zoezi\(\PageIndex{32}\)

    Sababu:\(20 h^{2}+13 h-15\)

    Jibu

    \((4 h-5)(5 h+3)\)

    Zoezi\(\PageIndex{33}\)

    Sababu:\(6 g^{2}+19 g-20\)

    Jibu

    \((q+4)(6 q-5)\)

    Zoezi\(\PageIndex{34}\)

    Sababu:\(2 x^{2}+6 x+5\)

    Jibu
    Je, kuna sababu kubwa ya kawaida? Hapana. .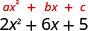
    Pata ac ac
      2 (5)
      10

    Pata namba mbili zinazozidisha hadi 10 na uongeze kwenye 6.

    Mambo ya 10 Jumla ya mambo
    1,10 1+10=11
    2, 5 2+5=7

    Hakuna mambo ambayo huzidisha hadi 10 na kuongeza hadi 6. Polynomial ni mkuu.

    Zoezi\(\PageIndex{35}\)

    Sababu:\(10 t^{2}+19 t-15\)

    Jibu

    \((2 t+5)(5 t-3)\)

    Zoezi\(\PageIndex{36}\)

    Sababu:\(3 u^{2}+8 u+5\)

    Jibu

    \((u+1)(3 u+5)\)

    Usisahau kuangalia kwa sababu ya kawaida!

    Zoezi\(\PageIndex{37}\)

    Sababu:\(10 y^{2}-55 y+70\)

    Jibu
    Je, kuna sababu kubwa ya kawaida? Ndiyo. GCF ni 5. .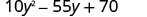
    Factor yake. Kuwa makini kuweka sababu ya 5 njia yote kupitia suluhisho! .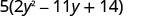
    Ya trinomial ndani ya mabano ina mgawo wa kuongoza ambao sio 1. .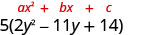
    Sababu ya trinomial. .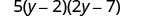
    Angalia kwa kuzidisha mambo yote matatu.  
    5\(\left(2 y^{2}-2 y-4 y+14\right)\)  
    5\(\left(2 y^{2}-11 y+14\right)\)  
    \(10 y^{2}-55 y+70\)✓
    Zoezi\(\PageIndex{38}\)

    Sababu:\(16 x^{2}-32 x+12\)

    Jibu

    4\((2 x-3)(2 x-1)\)

    Zoezi\(\PageIndex{39}\)

    Sababu:\(18 w^{2}-39 w+18\)

    Jibu

    3\((3 w-2)(2 w-3)\)

    Sasa tunaweza update awali factoring Mkakati, kama inavyoonekana katika Kielelezo\(\PageIndex{1}\) na kina katika Chagua mkakati wa sababu polynomials kabisa (updated), ni pamoja na trinomials ya fomu\(a x^{2}+b x+c\). Kumbuka, baadhi ya polynomials ni mkuu na hivyo hawawezi kuhesabiwa.

    Takwimu hii ina mkakati wa factoring polynomials. Juu ya takwimu ni GCF. Chini ya hii, kuna chaguzi tatu. Ya kwanza ni binomial. Ya pili ni trinomial. Chini ya trinomial kuna x squared + b x + c na x squared + b x +c. mbinu mbili hapa ni majaribio na makosa na “c” njia. Chaguo la tatu ni kwa maneno zaidi ya tatu. Ni kikundi.
    Kielelezo\(\PageIndex{1}\)
    CHAGUA MKAKATI WA SABABU POLYNOMIALS KABISA (UPDATED).
    1. Je, kuna sababu kubwa ya kawaida?
      • Factor yake.
    2. Je, polynomial ni binomial, trinomial, au kuna maneno zaidi ya tatu?
      • Ikiwa ni binomial, hivi sasa hatuna njia ya kuzingatia.
      • Kama ni trinomial ya fomu\(x^{2}+b x+c\)
        Tengeneza FOIL\\((x\qquad)(x\qquad)\).
      • Ikiwa ni trinomial ya fomu\(a x^{2}+b x+c\)
        Tumia Jaribio na Hitilafu au njia ya “ac”.
      • Ikiwa ina maneno zaidi ya tatu
        Tumia njia ya kikundi.
    3. Angalia kwa kuzidisha mambo.
    Kumbuka

    Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na factoring trinomials ya fomu\(a x^{2}+b x+c\)

    Dhana muhimu

    • Factor Trinomials ya Fomu kwa\(a x^{2}+b x+c\) kutumia Jaribio na Hitilafu: Angalia Mfano.
      1. Andika trinomial katika utaratibu wa kushuka kwa digrii.
      2. Pata jozi zote za muda wa kwanza.
      3. Pata jozi zote za muda wa tatu.
      4. Jaribu mchanganyiko wote unaowezekana wa mambo mpaka bidhaa sahihi inapatikana.
      5. Angalia kwa kuzidisha.
    • Factor Trinomials ya Fomu\(a x^{2}+b x+c\) Kutumia “ac” Method: Angalia Mfano.
      1. Sababu yoyote GCF.
      2. Pata ac ya bidhaa.
      3. Kupata namba mbili m na n kwamba:\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\)
      4. Split muda wa kati kwa kutumia m na n:
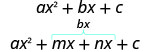
        Takwimu hii inaonyesha equations mbili. Equation juu inasoma mara x squared pamoja b mara x plus c. chini ya hii, ni equation mara x squared pamoja m mara x plus n mara x plus c. zaidi m mara x plus n mara x x ni mabano na b mara x juu yake.
      5. Sababu kwa kikundi.
      6. Angalia kwa kuzidisha mambo.
    • Chagua mkakati wa sababu polynomials kabisa (updated):
      1. Je, kuna sababu kubwa ya kawaida? Factor yake.
      2. Je, polynomial ni binomial, trinomial, au kuna maneno zaidi ya tatu?
        Ikiwa ni binomial, hivi sasa hatuna njia ya kuzingatia.
        Ikiwa ni trinomial ya fomu\(x^2+bx+c\)
        Tengeneza FOIL\((x\qquad)(x\qquad)\).
        Ikiwa ni trinomial ya fomu\(ax^2+bx+c\)
        Tumia Jaribio na Hitilafu au njia ya “ac”.
        Ikiwa ina maneno zaidi ya tatu
        Tumia njia ya kikundi.
      3. Angalia kwa kuzidisha mambo.

    faharasa

    mkuu wa polynomials
    Polynomials ambayo haiwezi kuhesabiwa ni polynomials mkuu.