Skip to main content
Global

6.6: Gawanya Polynomials

  1. Last updated
  2. Save as PDF
  • Page ID
    177781

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Gawanya polynomial na monomial
    • Gawanya polynomial na binomial
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Kuongeza:\(\dfrac{3}{d}+\dfrac{x}{d}\)
      Kama amekosa tatizo hili, kupitia Zoezi 1.7.1.
    2. kurahisisha:\(\dfrac{30 x y^{3}}{5 x y}\)
      Kama amekosa tatizo hili, mapitio Zoezi 6.5.37.
    3. Kuchanganya kama maneno:\(8 a^{2}+12 a+1+3 a^{2}-5 a+4\)
      Kama amekosa tatizo hili, mapitio Zoezi 1.3.37.

    Gawanya Polynomial na Monomial

    Katika sehemu ya mwisho, umejifunza jinsi ya kugawanya monomial na monomial. Unapoendelea kujenga ujuzi wako wa polynomials utaratibu unaofuata ni kugawanya polynomial ya maneno mawili au zaidi na monomial.

    Njia tutakayotumia kugawanya polynomial na monomial inategemea mali ya kuongeza sehemu. Hivyo tutaweza kuanza na mfano kupitia sehemu Aidha.

    \(\begin{array}{ll}{\text { The sum, }} & {\dfrac{y}{5}+\dfrac{2}{5}} \\ {\text { simplifies to }} & {\dfrac{y+2}{5}}\end{array}\)

    Sasa tutafanya hivyo kwa reverse ili kugawanya sehemu moja katika vipande tofauti.

    Tutaweza hali sehemu ya kuongeza mali hapa kama wewe kujifunza na katika reverse.

    SEHEMU YA KUONGEZA

    Ikiwa a, b, na c ni namba ambapo\(c\neq 0\), basi

    \[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \quad \text { and } \quad \dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\]

    Tunatumia fomu upande wa kushoto ili kuongeza sehemu ndogo na tunatumia fomu kwa haki ya kugawanya polynomial na monomial.

    \(\begin{array}{ll}{\text { For example, }} & {\dfrac{y+2}{5}} \\ {\text { can be written }} & {\dfrac{y}{5}+\dfrac{2}{5}}\end{array}\)

    Tunatumia fomu hii ya kuongeza sehemu ili kugawanya polynomials na monomials.

    MGAWANYIKO WA POLYNOMIAL NA MONOMIAL

    Ili kugawanya polynomial na monomial, kugawanya kila neno la polynomial na monomial.

    Zoezi\(\PageIndex{1}\)

    Pata quotient:\(\dfrac{7 y^{2}+21}{7}\)

    Jibu

    \(\begin{array}{ll} & \dfrac{7 y^{2}+21}{7}\\\text{Divide each term of the numerator by the denominator.} & \dfrac{7 y^{2}}{7}+\dfrac{21}{7} \\ \text {Simplify each fraction. } & y^{2}+3 \end{array}\)

    Zoezi\(\PageIndex{2}\)

    Pata quotient:\(\dfrac{8 z^{2}+24}{4}\)

    Jibu

    \(2 z^{2}+6\)

    Zoezi\(\PageIndex{3}\)

    Pata quotient:\(\dfrac{18 z^{2}-27}{9}\)

    Jibu

    \(2 z^{2}-3\)

    Kumbuka kwamba mgawanyiko unaweza kuwakilishwa kama sehemu. Unapoulizwa kugawanya polynomial na monomial na si tayari katika fomu ya sehemu, andika sehemu na polynomial katika nambari na monomial katika denominator.

    Zoezi\(\PageIndex{4}\)

    Pata quotient:\(\left(18 x^{3}-36 x^{2}\right) \div 6 x\)

    Jibu

    \(\begin{array}{ll} & \left(18 x^{3}-36 x^{2}\right) \div 6 x\\\text { Rewrite as a fraction. } & \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}}{6 x}-\dfrac{36 x^{2}}{6 x}\\ \text { Simplify. } &3 x^{2}-6 x\end{array}\)

    Zoezi\(\PageIndex{5}\)

    Pata quotient:\(\left(27 b^{3}-33 b^{2}\right) \div 3 b\)

    Jibu

    \(9 b^{2}-11 b\)

    Zoezi\(\PageIndex{6}\)

    Pata quotient:\(\left(25 y^{3}-55 y^{2}\right) \div 5 y\)

    Jibu

    \(5 y^{2}-11 y\)

    Tunapogawanya na hasi, lazima tuwe makini zaidi na ishara.

    Zoezi\(\PageIndex{7}\)

    Pata quotient:\(\dfrac{12 d^{2}-16 d}{-4}\)

    Jibu

    \(\begin{array}{ll} &\dfrac{12 d^{2}-16 d}{-4}\\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Simplify. Remember, subtracting a negative is like adding a positive! }& -3 d^{2}+4 d\end{array}\)

    Zoezi\(\PageIndex{8}\)

    Pata quotient:\(\dfrac{25 y^{2}-15 y}{-5}\)

    Jibu

    \(-5 y^{2}+3 y\)

    Zoezi\(\PageIndex{9}\)

    Pata quotient:\(\dfrac{42 b^{2}-18 b}{-6}\)

    Jibu

    \(-7 b^{2}+3 b\)

    Zoezi\(\PageIndex{10}\)

    Pata quotient:\(\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\)

    Jibu

    \(\begin{array}{ll} &\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\\ \text { Separate the terms. }& \dfrac{105 y^{5}}{5 y^{2}}+\dfrac{75 y^{3}}{5 y^{2}}\\ \text { Simplify. }& 21 y^{3}+15 y\end{array}\)

    Zoezi\(\PageIndex{11}\)

    Pata quotient:\(\dfrac{60 d^{7}+24 d^{5}}{4 d^{3}}\)

    Jibu

    \(15 d^{4}+6 d^{2}\)

    Zoezi\(\PageIndex{12}\)

    Pata quotient:\(\dfrac{216 p^{7}-48 p^{5}}{6 p^{3}}\)

    Jibu

    \(36 p^{4}-8 p^{2}\)

    Zoezi\(\PageIndex{13}\)

    Pata quotient:\(\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\)

    Jibu

    \(\begin{array}{ll} &\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\\ \text { Rewrite as a fraction. }& \dfrac{15 x^{3} y-35 x y^{2}}{-5 x y}\\\text { Separate the terms. Be careful with the signs! }& \dfrac{15 x^{3} y}{-5 x y}-\dfrac{35 x y^{2}}{-5 x y}\\ \text { Simplify. } & -3 x^{2}+7 y\end{array}\)

    Zoezi\(\PageIndex{14}\)

    Pata quotient:\(\left(32 a^{2} b-16 a b^{2}\right) \div(-8 a b)\)

    Jibu

    \(-4 a+2 b\)

    Zoezi\(\PageIndex{15}\)

    Pata quotient:\(\left(-48 a^{8} b^{4}-36 a^{6} b^{5}\right) \div\left(-6 a^{3} b^{3}\right)\)

    Jibu

    \(8 a^{5} b+6 a^{3} b^{2}\)

    Zoezi\(\PageIndex{13}\)

    Pata quotient:\(\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\)

    Jibu

    \(\begin{array}{ll} &\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\\\text { Separate the terms. }& \dfrac{36 x^{3} y^{2}}{9 x^{2} y}+\dfrac{27 x^{2} y^{2}}{9 x^{2} y}-\dfrac{9 x^{2} y^{3}}{9 x^{2} y}\\ \text { Simplify. } & 4 x y+3 y-y^{2}\end{array}\)

    Zoezi\(\PageIndex{14}\)

    Pata quotient:\(\dfrac{40 x^{3} y^{2}+24 x^{2} y^{2}-16 x^{2} y^{3}}{8 x^{2} y}\)

    Jibu

    \(5 x y+3 y-2 y^{2}\)

    Zoezi\(\PageIndex{15}\)

    Pata quotient:\(\dfrac{35 a^{4} b^{2}+14 a^{4} b^{3}-42 a^{2} b^{4}}{7 a^{2} b^{2}}\)

    Jibu

    \(5 a^{2}+2 a^{2} b-6 b^{2}\)

    Zoezi\(\PageIndex{16}\)

    Pata quotient:\(\dfrac{10 x^{2}+5 x-20}{5 x}\)

    Jibu

    \(\begin{array}{ll}&\dfrac{10 x^{2}+5 x-20}{5x}\\\text { Separate the terms. }& \dfrac{10 x^{2}}{5 x}+\dfrac{5 x}{5 x}-\dfrac{20}{5 x}\\ \text { Simplify. } &2 x+1-\dfrac{4}{x}\end{array}\)

    Zoezi\(\PageIndex{17}\)

    Pata quotient:\(\dfrac{18 c^{2}+6 c-9}{6 c}\)

    Jibu

    \(3 c+1-\dfrac{3}{2 c}\)

    Zoezi\(\PageIndex{18}\)

    Pata quotient:\(\dfrac{10 d^{2}-5 d-2}{5 d}\)

    Jibu

    \(2 d-1-\dfrac{2}{5 d}\)

    Gawanya Polynomial na Binomial

    Ili kugawanya polynomial na binomial, tunafuata utaratibu sawa na mgawanyiko mrefu wa idadi. Basi hebu tuangalie kwa makini hatua tunazochukua wakati tunagawanya nambari ya tarakimu 3, 875, na namba ya tarakimu 2, 25.

    Tunaandika mgawanyiko mrefu 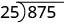Mgawanyiko wa muda mrefu wa 875 na 25.
    Tunagawanya tarakimu mbili za kwanza, 87, na 25. 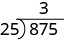25 inafaa katika 87 mara tatu. 3 imeandikwa juu ya tarakimu ya pili ya 875 katika mabano ya mgawanyiko mrefu.
    Tunazidisha mara 3 25 na kuandika bidhaa chini ya 87. 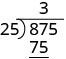Bidhaa ya 3 na 25 ni 75, ambayo imeandikwa chini ya tarakimu mbili za kwanza za 875 katika bracket ya mgawanyiko mrefu.
    Sasa tunaondoa 75 kutoka 87. 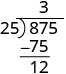87 minus 75 ni 12, ambayo imeandikwa chini ya 75.
    Kisha sisi kuleta chini tarakimu ya tatu ya mgao, 5. 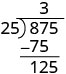The 5 katika 875 ni kuletwa chini karibu na 12, na kufanya 125.
    Kurudia mchakato, kugawanya 25 hadi 125. 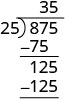25 inafaa katika 125 mara tano. 5 imeandikwa kwa haki ya 3 juu ya bracket ya mgawanyiko mrefu. Mara 5 25 ni 125. 125 chini 125 ni sifuri. Kuna sifuri salio, hivyo 25 inafaa katika 125 hasa mara tano. 875 kugawanywa na 25 sawa 35.

    Tunaangalia mgawanyiko kwa kuzidisha quotient na mgawanyiko.

    Ikiwa tulifanya mgawanyiko kwa usahihi, bidhaa lazima iwe sawa na mgao.

    \[\begin{array}{l}{35 \cdot 25} \\ {875}\checkmark\end{array}\]

    Sasa tutagawanya trinomial na binomial. Unaposoma kupitia mfano, angalia jinsi hatua zilivyo sawa na mfano wa namba hapo juu.

    Zoezi\(\PageIndex{19}\)

    Pata quotient:\(\left(x^{2}+9 x+20\right) \div(x+5)\)

    Jibu
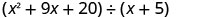
      Trinomial, x mraba pamoja na 9 x pamoja na 20, imegawanywa na binomial, x pamoja na 5.
    Andika kama tatizo la mgawanyiko mrefu.  
    Kuwa na uhakika mgao ni katika hali ya kawaida. 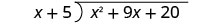Mgawanyiko wa muda mrefu wa x mraba pamoja na 9 x pamoja na 20 na x pamoja na 5
    Gawanya x 2 na x. Inaweza kusaidia kujiuliza, “Ninahitaji nini kuzidisha x na kupata x 2?”  
    Weka jibu, x, katika quotient juu ya muda x. 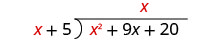x inafaa katika x squared x nyati. x imeandikwa juu ya muda wa pili wa x squared pamoja 9 x plus 20 katika muda mrefu mgawanyiko mabano.
    Kuzidisha x mara x + 5. Line up maneno kama chini ya mgao. 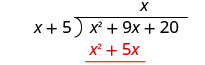Bidhaa ya x na x plus 5 ni x squared pamoja 5 x, ambayo imeandikwa chini ya masharti mawili ya kwanza ya x squared pamoja 9x plus 20 katika muda mrefu mgawanyiko bracket.
    Ondoa x 2 + 5 x kutoka x 2 + 9 x.  
    Unaweza kupata ni rahisi kubadili ishara na kisha kuongeza.
    Kisha kuleta chini ya muda wa mwisho, 20.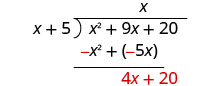    		 Jumla ya x squared pamoja na 9 x x na hasi x squared pamoja hasi 5 x ni 4 x, ambayo imeandikwa chini ya hasi 5 x mrefu wa tatu katika x squared pamoja 9 x pamoja 20 ni kuletwa chini karibu na 4 x, na kufanya 4 x pamoja 20.
    Gawanya 4 x na x. Inaweza kusaidia kujiuliza, “Ninahitaji nini
    kuzidisha x na kupata 4 x?”    		  
    Weka jibu, 4, katika quotient juu ya muda wa mara kwa mara. 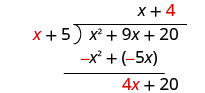4 x kugawanywa na x ni 4. Plus 4 imeandikwa juu ya muda mrefu mgawanyiko mabano, karibu na x na juu ya 20 katika x squared pamoja 9 x plus 20.
    Kuzidisha mara 4 x + 5. 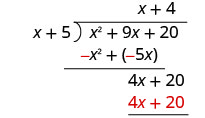x pamoja mara 5 4 ni 4 x plus 20, ambayo imeandikwa chini ya kwanza 4 x pamoja 20.
    Ondoa 4 x + 20 kutoka 4 x + 20. 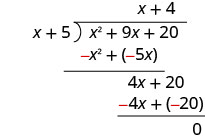4 x pamoja 20 minus 4 x pamoja 20 ni 0. salio ni 0. x squared pamoja 9 x plus 20 kugawanywa na x plus 5 sawa x plus 4.
    Angalia:  
    Panua quotient na mgawanyiko.  
    (x + 4) (x + 5)  
    Unapaswa kupata mgao.  
    x 2 + 9 x + 20 ✓
    Zoezi\(\PageIndex{20}\)

    Pata quotient:\(\left(y^{2}+10 y+21\right) \div(y+3)\)

    Jibu

    y+7

    Zoezi\(\PageIndex{21}\)

    Pata quotient:\(\left(m^{2}+9 m+20\right) \div(m+4)\)

    Jibu

    m+5

    Wakati mgawanyiko ina Ondoa ishara, ni lazima kuwa makini zaidi wakati sisi kuzidisha quotient sehemu na kisha Ondoa. Inaweza kuwa salama kuonyesha kwamba tunabadilisha ishara na kisha kuongeza.

    Zoezi\(\PageIndex{22}\)

    Pata quotient:\(\left(2 x^{2}-5 x-3\right) \div(x-3)\)

    Jibu
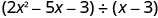
      Trinomial, 2 x squared minus 5 x minus 3, imegawanywa na binomial, x minus 3.
    Andika kama tatizo la mgawanyiko mrefu.  
    Kuwa na uhakika mgao ni katika hali ya kawaida. 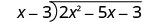Mgawanyiko mrefu wa 2 x squared minus 5 x minus 3 na x minus 3.
    Gawanya 2 x 2 na x.
    Weka jibu, 2 x, katika quotient juu ya muda x.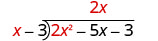    		 x inafaa katika 2 x squared 2 x mara. 2 x imeandikwa juu ya muda wa pili wa 2 x squared minus 5 x minus 3 katika muda mrefu mgawanyiko bracket.
    Kuzidisha 2 x mara x - 3. Line up maneno kama chini ya mgao. 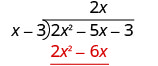Bidhaa ya 2 x na x minus 3 ni 2 x squared minus 6 x, ambayo imeandikwa chini ya masharti mawili ya kwanza ya 2 x squared minus 5 x bala 3 katika muda mrefu mgawanyiko bracket.
    Ondoa 2 x 2 - 6 x kutoka 2 x 2 - 5 x.
    Badilisha ishara na kisha uongeze.
    Kisha kuleta chini muda wa mwisho.    		 Jumla ya 2 x mraba bala 5 x na hasi 2 x squared pamoja 6 x ni x, ambayo imeandikwa chini ya 6 x mrefu ya tatu katika 2 x squared bala 5 x bala 3 ni kuletwa chini karibu na x, na kufanya x minus 3.
    Gawanya x na x.
    Weka jibu, 1, katika quotient juu ya muda wa mara kwa mara.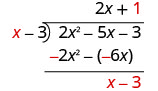    		 Plus 1 imeandikwa juu ya bracket ya mgawanyiko mrefu, karibu na 2 x na juu ya minus 3 katika 2 x squared minus 5 x minus 3.
    Panua mara 1 x - 3. 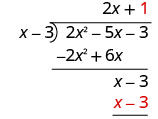x minus mara 3 1 ni x minus 3, ambayo imeandikwa chini ya kwanza x minus 3.
    Ondoa x - 3 kutoka x - 3 kwa kubadilisha ishara na kuongeza. 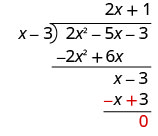Binomial x minus 3 minus bala binomial hasi x pamoja 3 ni 0. Salio ni 0. 2 x squared minus 5 x minus 3 imegawanywa na x minus 3 sawa 2 x plus 1.
    Kuangalia, kuzidisha (x - 3) (2 x + 1).  
    Matokeo yake yanapaswa kuwa 2 x 2 - 5 x -3.
    Zoezi\(\PageIndex{23}\)

    Pata quotient:\(\left(2 x^{2}-3 x-20\right) \div(x-4)\)

    Jibu

    2x+5

    Zoezi\(\PageIndex{24}\)

    Pata quotient:\(\left(3 x^{2}-16 x-12\right) \div(x-6)\)

    Jibu

    3x+2

    Wakati sisi kugawanywa 875 na 25, hatukuwa na salio. Lakini wakati mwingine mgawanyiko wa idadi haina kuondoka salio. Vile vile ni kweli wakati tunagawanya polynomials. Katika Zoezi\(\PageIndex{25}\), tutakuwa na mgawanyiko kwamba majani salio. Tunaandika salio kama sehemu na mgawanyiko kama denominator.

    Zoezi\(\PageIndex{25}\)

    Pata quotient:\(\left(x^{3}-x^{2}+x+4\right) \div(x+1)\)

    Jibu
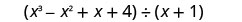
      Polynomial, x cubed minus x squared pamoja x pamoja na 4, kugawanywa na mwingine polynomial, x pamoja 1.
    Andika kama tatizo la mgawanyiko mrefu.  
    Kuwa na uhakika mgao ni katika hali ya kawaida. 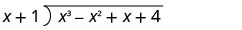Mgawanyiko wa muda mrefu wa x cubed minus x squared pamoja x plus 4 na x plus 1.
    Gawanya x 3 na x.
    Weka jibu, x 2, katika quotient juu ya muda x 2.
    Kuzidisha x mara 2 x + 1. Line up maneno kama chini ya mgao.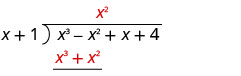    		 x inafaa katika x squared x nyati. x imeandikwa juu ya muda wa pili wa x cubed minus x squared pamoja x plus 4 katika muda mrefu mgawanyiko mabano.
    Ondoa x 3 + x 2 kutoka x 3 - x 2 kwa kubadilisha ishara na kuongeza.
    Kisha kuleta chini ya muda ujao.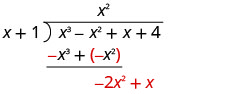    		 Jumla ya x cubed minus x squared na hasi x cubed pamoja hasi x squared ni hasi 2 x squared, ambayo imeandikwa chini ya x squared hasi. Muda unaofuata katika x cubed minus x squared pamoja x pamoja na 4 ni kuletwa chini karibu na hasi 2 x squared, na kufanya hasi 2 x squared pamoja x.
    Gawanya -1 x 2 na x.
    Weka jibu, -1 x, katika quotient juu ya muda x.
    Kuzidisha -1 x mara x + 1. Line up maneno kama chini ya mgao.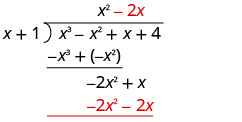    		 Minus 2 x imeandikwa juu ya bracket ya mgawanyiko mrefu, karibu na x mraba na juu ya x katika x cubed minus x squared pamoja x plus 4. Hasi 2 x mraba minus 2 x imeandikwa chini ya hasi 2 x squared pamoja x.
    Ondoa -2 x 2 - 2 x kutoka -2 x 2 + x kwa kubadilisha ishara na kuongeza.
    Kisha kuleta chini muda wa mwisho.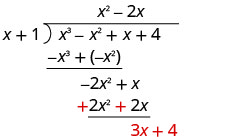    		 Jumla ya hasi 2 x squared pamoja x na 2 x squared pamoja 2 x inapatikana kuwa 3 x. muda wa mwisho katika x cubed bala x squared pamoja x pamoja x 4 ni kuletwa chini, na kufanya 3 x pamoja 4.
    Gawanya 3 x na x.
    Weka jibu, 3, katika quotient juu ya muda wa mara kwa mara.
    Panua mara 3 x + 1. Line up maneno kama chini ya mgao.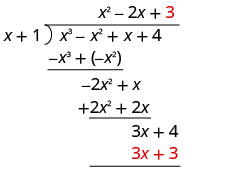    		 Plus 3 imeandikwa juu ya mabano ya mgawanyiko mrefu, juu ya 4 katika x cubed minus x squared pamoja x plus 4. 3 x plus 3 imeandikwa chini ya 3 x plus 4.
    Ondoa 3 x + 3 kutoka 3 x + 4 kwa kubadilisha ishara na kuongeza.
    Andika salio kama sehemu na mgawanyiko kama denominator.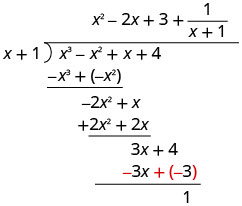    		 Jumla ya 3 x pamoja na 4 na hasi 3 x pamoja na hasi 3 ni 1. Kwa hiyo, polynomial x cubed minus x squared pamoja x pamoja 4, kugawanywa na x binomial pamoja 1, sawa x squared bala 2 x pamoja sehemu 1 juu ya x pamoja 1.
    Kuangalia,\((x+1)\left(x^{2}-2 x+3+\dfrac{1}{x+1}\right)\)
    kuzidisha Matokeo lazima\(x^{3}-x^{2}+x+4\)
    Zoezi\(\PageIndex{26}\)

    Pata quotient:\(\left(x^{3}+5 x^{2}+8 x+6\right) \div(x+2)\)

    Jibu

    \(x^{2}+3 x+2+\dfrac{2}{x+2}\)

    Zoezi\(\PageIndex{27}\)

    Pata quotient:\(\left(2 x^{3}+8 x^{2}+x-8\right) \div(x+1)\)

    Jibu

    \(2 x^{2}+6 x-5-\dfrac{3}{x+1}\)

    Angalia nyuma kwenye gawio katika Mfano, Mfano, na Mfano. Masharti yaliandikwa katika utaratibu wa kushuka kwa digrii, na hapakuwa na digrii zilizopo. mgao katika Mfano itakuwa\(x^{4}-x^{2}+5 x-2\). Inakosa\(x^{3}\) muda. Sisi kuongeza katika\(0x^{3}\) kama kishika.

    Zoezi\(\PageIndex{28}\)

    Pata quotient:\(\left(x^{4}-x^{2}+5 x-2\right) \div(x+2)\)

    Jibu

    Kumbuka kwamba hakuna\(x^{3}\) mrefu katika mgao. Sisi kuongeza\(0x^{3}\) kama kishika.

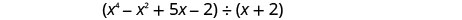
      Polynomial, x kwa nguvu ya nne minus x squared minus 5 x minus 2, kugawanywa na mwingine polynomial, x pamoja 2.
    Andika kama tatizo la mgawanyiko mrefu. Kuwa na uhakika mgao ni katika hali ya kawaida na placeholders kwa masharti kukosa. 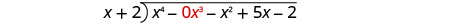Mgawanyiko wa muda mrefu wa x hadi nguvu ya nne pamoja na 0 x cubed minus x squared minus 5 x 2 na x pamoja 2.
    Gawanya x 4 na x.
    Weka jibu, x 3, katika quotient juu ya muda x 3.
    Kuzidisha x mara 3 x + 2. Weka masharti kama hayo.
    Ondoa na kisha kuleta chini ya muda ujao.    		 x cubed imeandikwa juu ya muda mgawanyiko mabano juu x cubed mrefu katika mgao. Chini ya masharti mawili ya kwanza ya mgao x kwa nguvu ya nne pamoja 2 x cubed ni subtracted kutoa hasi 2 x cubed minus x squared. Maelezo yaliyo karibu na mgawanyiko yanasoma “Inaweza kuwa na manufaa kubadili ishara na kuongeza.”
    Gawanya -1 x 3 na x.
    Weka jibu, -2 x 2, katika quotient juu ya muda x 2.
    Kuzidisha -1 x 2 mara x + 1. Weka masharti kama hayo.
    Ondoa na kuleta chini ya muda ujao.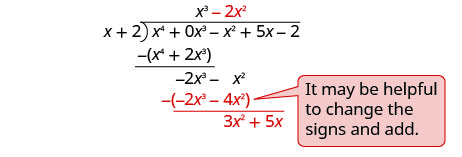    		 x cubed minus 2 x squared imeandikwa juu ya muda mrefu mgawanyiko bracket. Chini ya mgawanyiko wa muda mrefu hasi 2 x cubed minus 4 x squared ni subtracted kutoa 3 x squared pamoja 5 x. kumbuka anasoma “Inaweza kuwa na manufaa kwa mabadiliko ya ishara na kuongeza.”
    Gawanya 3 x 2 na x.
    Weka jibu, 3 x, katika quotient juu ya muda x.
    Kuzidisha mara 3 x + 1. Weka masharti kama hayo.
    Ondoa na kuleta chini ya muda ujao.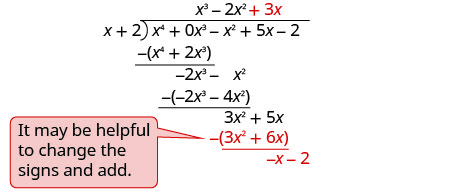    		 x cubed minus 2 x squared pamoja 3 x imeandikwa juu ya muda mrefu mgawanyiko bracket. Chini ya mgawanyiko wa muda mrefu 3 x mraba pamoja na 6 x hutolewa ili kutoa hasi x minus 2. Maelezo yanasoma “Inaweza kuwa na manufaa kubadili ishara na kuongeza.”
    Gawanya - x kwa x.
    Weka jibu, -1, katika quotient juu ya muda wa mara kwa mara.
    Kuzidisha -1 mara x + 1. Weka masharti kama hayo.
    Badilisha ishara, ongeza.    		 x cubed minus 2 x squared pamoja 3 x minus 1 imeandikwa juu ya muda mrefu mgawanyiko bracket. Chini ya mgawanyiko mrefu hasi x minus 2 ni Ondoa kutoa 0. Maelezo yanasoma “Inaweza kuwa na manufaa kubadili ishara na kuongeza.” Polynomial x kwa nguvu ya nne minus x squared pamoja 5 x minus 2, kugawanywa na x binomial pamoja 2 sawa na polynomial x cubed minus 2 x squared pamoja 3 x minus 1.
    Kuangalia, kuzidisha\((x+2)\left(x^{3}-2 x^{2}+3 x-1\right)\)  
    Matokeo yake yanapaswa kuwa\(x^{4}-x^{2}+5 x-2\)
    Zoezi\(\PageIndex{29}\)

    Pata quotient:\(\left(x^{3}+3 x+14\right) \div(x+2)\)

    Jibu

    \(x^{2}-2 x+7\)

    Zoezi\(\PageIndex{30}\)

    Pata quotient:\(\left(x^{4}-3 x^{3}-1000\right) \div(x+5)\)

    Jibu

    \(x^{3}-8 x^{2}+40 x-200\)

    Katika Zoezi\(\PageIndex{31}\), tutagawanya na\(2a−3\). Kama sisi kugawanya tutakuwa na kuzingatia constants kama vile vigezo.

    Zoezi\(\PageIndex{31}\)

    Pata quotient:\(\left(8 a^{3}+27\right) \div(2 a+3)\)

    Jibu

    Wakati huu tutaonyesha mgawanyiko wote kwa hatua moja. Tunahitaji kuongeza placeholders mbili ili kugawanya.

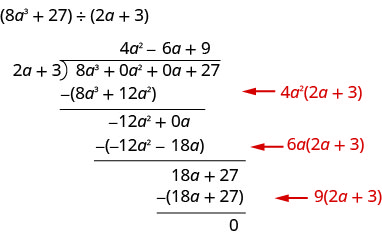
    Takwimu inaonyesha mgawanyiko mrefu wa 8 cubed pamoja 27 na 2 pamoja na 3. Katika bracket ya mgawanyiko wa muda mrefu, wawekaji wa nafasi 0 mraba na 0 a huongezwa kwenye polynomial. Kwenye mstari wa kwanza chini ya mgao 8 cubed pamoja na 12 mraba hutolewa. Kwa upande wa kulia, mshale unaonyesha kwamba thamani hii ilitoka kuzidisha 4 mraba na 2 pamoja na 3. Ondoa hutoa hasi 12 mraba pamoja na 0 a. kutoka hasi hii 12 mraba minus 18 a hutolewa. Kwa upande wa kulia, mshale unaonyesha kwamba thamani hii ilitoka kuzidisha 6 a na 2 pamoja na 3. Kutoa kutoa 18 pamoja na 27. Kutoka hii 18 pamoja na 27 imeondolewa. Kwa upande wa kulia, mshale unaonyesha kwamba thamani hii ilitoka kuzidisha 9 na 2 pamoja na 3. Matokeo yake ni 0.

    Kuangalia, kuzidisha\((2 a+3)\left(4 a^{2}-6 a+9\right)\)

    Matokeo yake yanapaswa kuwa\(8 a^{3}+27\)

    Zoezi\(\PageIndex{32}\)

    Pata quotient:\(\left(x^{3}-64\right) \div(x-4)\)

    Jibu

    \(x^{2}+4 x+16\)

    Zoezi\(\PageIndex{33}\)

    Pata quotient:\(\left(125 x^{3}-8\right) \div(5 x-2)\)

    Jibu

    \(25 x^{2}+10 x+4\)

    Kumbuka

    Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kugawa polynomials:

    • Gawanya Polynomial na Monomial
    • Gawanya Polynomial na Monomial 2
    • Gawanya Polynomial na Binomial

    Dhana muhimu

    • Sehemu ya kuongeza
      • Ikiwa a, b, na c ni namba ambapo\(c\neq 0\), basi
        \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\) na\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\)
    • Idara ya Polynomial na Monomial
      • Ili kugawanya polynomial na monomial, kugawanya kila neno la polynomial na monomial.