Skip to main content
Global

5.3: Tatua Mifumo ya Equations kwa Kuondoa

  1. Last updated
  2. Save as PDF
  • Page ID
    177341

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza

    Mwishoni mwa sehemu hii, utaweza:

    • Tatua mfumo wa equations kwa kuondoa
    • Tatua matumizi ya mifumo ya equations kwa kuondoa
    • Chagua njia rahisi zaidi ya kutatua mfumo wa equations linear
    Kumbuka

    Kabla ya kuanza, fanya jaribio hili la utayari.

    1. Rahisisha -5 (6—3a).
      Kama amekosa tatizo hili, kupitia Zoezi 1.10.43.
    2. Kutatua equation\(\frac{1}{3}x+\frac{5}{8}=\frac{31}{24}\).
      Ikiwa umekosa tatizo hili, kagua Zoezi 2.5.1.

    Tumetatua mifumo ya equations linear kwa graphing na kwa badala. Graphing kazi vizuri wakati coefficients variable ni ndogo na ufumbuzi ina maadili integer. Badala kazi vizuri wakati tunaweza kwa urahisi kutatua equation moja kwa moja ya vigezo na kuwa na sehemu nyingi mno katika kujieleza kusababisha.

    Njia ya tatu ya kutatua mifumo ya usawa wa mstari inaitwa Njia ya Kuondoa. Wakati sisi kutatuliwa mfumo kwa badala, sisi ilianza na equations mbili na vigezo mbili na kupunguza kwa equation moja na variable moja. Hii ndio tutafanya na njia ya kuondoa, pia, lakini tutakuwa na njia tofauti ya kufika huko.

    Tatua Mfumo wa Equations kwa Kuondoa

    Njia ya Kuondoa inategemea Mali ya Kuongeza ya Usawa. Mali ya Kuongezea ya Usawa inasema kwamba unapoongeza kiasi sawa kwa pande zote mbili za usawa, bado una usawa. Tutaongeza Mali ya Kuongeza ya Usawa kusema kwamba unapoongeza kiasi sawa kwa pande zote mbili za equation, matokeo ni sawa.

    Kwa maneno yoyote a, b, c, na d,

    \[\begin{array}{lc} \text{ if } & a=b \\ \text { and } & c=d \\ \text { then } &a+c =b+d \end{array}\]

    Ili kutatua mfumo wa equations kwa kuondoa, tunaanza na equations zote mbili katika fomu ya kawaida. Kisha tunaamua ni aina gani ya kutofautiana itakuwa rahisi kuondokana. Tunaamuaje? Tunataka kuwa na coefficients ya variable moja kuwa kinyume, ili tuweze kuongeza equations pamoja na kuondoa kwamba variable.

    Angalia jinsi kwamba kazi wakati sisi kuongeza equations hizi mbili pamoja:

    \[\begin{array}{l} 3x+y=5 \\ \underline{2x-y=0} \\ 5x\quad\quad=5\end{array}\]

    y ya kuongeza sifuri na tuna equation moja na variable moja.

    Hebu jaribu mwingine:

    \[\left\{\begin{array}{l}{x+4 y=2} \\ {2 x+5 y=-2}\end{array}\right.\]

    Wakati huu hatuoni variable ambayo inaweza kuondolewa mara moja kama sisi kuongeza equations.

    Lakini ikiwa tunazidisha equation ya kwanza kwa -1, tutafanya coefficients ya kinyume x. Lazima tuzidishe kila neno pande zote mbili za equation kwa -1.

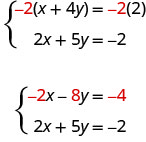
    Takwimu hii inaonyesha equations mbili. Ya kwanza ni hasi 2 mara x pamoja 4y katika mabano sawa hasi 2 mara 2. Ya pili ni 2x + 5y = hasi 2. Takwimu hii inaonyesha equations mbili. Ya kwanza ni hasi 2x minus 8y = hasi 4. Ya pili ni 2x + 5y = -hasi 2.

    Sasa tunaona kwamba coefficients ya maneno x ni kinyume, hivyo x itaondolewa wakati sisi kuongeza equations hizi mbili.

    Ongeza equations mwenyewe—matokeo yanapaswa kuwa -3 y = -6. Na kwamba inaonekana rahisi kutatua, siyo hivyo? Hapa ni nini ingekuwa kuangalia kama.

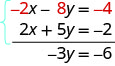
    Takwimu hii inaonyesha milinganyo miwili inayoongezwa pamoja. Ya kwanza ni hasi 2x — 8y = -4 na 2x pamoja na 5y = hasi 2. Jibu ni hasi 3y = hasi 6.

    Tutafanya moja zaidi:

    \[\left\{\begin{array}{l}{4 x-3 y=10} \\ {3 x+5 y=-7}\end{array}\right.\]

    Haionekani kwamba tunaweza kupata coefficients ya variable moja kuwa kinyume kwa kuzidisha moja ya equations na mara kwa mara, isipokuwa sisi kutumia sehemu ndogo. Hivyo badala yake, tutaweza kuwa na kuzidisha equations wote kwa mara kwa mara.

    Tunaweza kufanya coefficients ya x kuwa kinyume kama sisi kuzidisha equation kwanza na 3 na ya pili kwa -4, hivyo sisi kupata 12 x na -12 x.

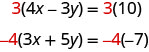
    Takwimu hii inaonyesha equations mbili. Ya kwanza ni mara 3 4x minus 3y katika mabano sawa mara 3 10. Ya pili ni hasi mara 4 3x pamoja na 5y katika mabano sawa hasi mara 4 hasi 7.

    Hii inatupa equations hizi mbili mpya:

    \[\left\{\begin{aligned} 12 x-9 y &=30 \\-12 x-20 y &=28 \end{aligned}\right.\]

    Tunapoongeza milinganyo haya,

    \[\[\left\{\begin{array}{r}{12 x-9 y=30} \\ {\underline{-12 x-20 y=28}} \\\end{array}\right.\\\quad\qquad {-29 y=58}\]\]

    x ya ni kuondolewa na sisi tu na -29 y = 58.

    Mara baada ya sisi kupata equation na variable moja tu, sisi kutatua hilo. Kisha sisi badala kwamba thamani katika moja ya equations awali kutatua kwa variable iliyobaki. Na, kama siku zote, tunaangalia jibu letu ili kuhakikisha kuwa ni suluhisho kwa equations zote za awali.

    Sasa tutaona jinsi ya kutumia kuondoa kutatua mfumo huo wa equations sisi kutatuliwa kwa graphing na badala.

    Zoezi\(\PageIndex{1}\): How to Solve a System of Equations by Elimination

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{2 x+y=7} \\ {x-2 y=6}\end{array}\right.\)

    Jibu

    Takwimu hii ina safu saba na nguzo tatu. Mstari wa kwanza unasoma, “Hatua ya 1. Andika equations zote mbili kwa fomu ya kawaida. Ikiwa coefficients yoyote ni sehemu ndogo, wazi yao.” Pia inasema, “Equations zote mbili ziko katika fomu ya kawaida, A x + B y = C. hakuna sehemu ndogo.” Pia inatoa milinganyo miwili kama 2x + y = 7 na x - 2y = 6.Mstari wa pili unasoma, “Hatua ya 2: Fanya coefficients ya kinyume kimoja cha kutofautiana. Chagua ni variable gani utaondoa. Panua equations moja au zote mbili ili coefficients ya variable hiyo ni kinyume.” Pia inasema, “Tunaweza kuondokana na y kwa kuzidisha equation kwanza kwa 2. Panua pande zote mbili za 2x + y = 7 na 2.” Pia inaonyesha hatua na equations. Awali milinganyo ni ex + y = 7 na x — 2y = 6. Kisha huwa 2 (2x + y) = mara 2 7 na x - 2y = 6. Wao kisha kuwa 4x + 2y = 14 na x — 2y = 6.Mstari wa tatu unasema, “Hatua ya 3: Ongeza milinganyo inayotokana na hatua ya 2 ili kuondoa tofauti moja.” Pia inasema, “Sisi kuongeza x ya, y, na constants.” Kisha anatoa equation kama 5x = 20.Mstari wa nne unasema, “Hatua ya 4: Tatua kwa kutofautiana iliyobaki.” Pia inasema, “Tatua kwa x.” Inatoa equation kama x = 4.Mstari wa tano unasema, “Hatua ya 5: Badilisha suluhisho kutoka Hatua ya 4 kwenye moja ya milinganyo ya awali. Kisha kutatua kwa variable nyingine.” Pia anasema, “Mbadala x = 4 katika equation pili, x - 2y = 6. Kisha kutatua kwa ajili ya y.” Kisha anatoa milinganyo kama x - 2y = 6 ambayo inakuwa 4 - 2y = 6. Hii ni kisha -2y = 2, na hivyo, y = -1.Mstari wa sita unasema, “Hatua ya 6: Andika suluhisho kama jozi ya amri.” Pia inasema, “Andika kama (x, y).” Inatoa jozi zilizoamriwa kama (4, -1).Mstari wa saba unasema, “Hatua ya 7: Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.” Pia inasema, “Mbadala (4, -1) katika 2x + y = 7 na x — 2y = 6. Je, wanafanya equations zote mbili kweli? Ndiyo!” Kisha hutoa milinganyo. 2x + y = 7 inakuwa mara 2 4 + -1 = 7 ambayo ni 7 = 7. x — 2y = 6 inakuwa 4 — mara 2 -1 = 6 ambayo ni 6 = 6. Mstari huo unasema, “Suluhisho ni (4, -1).”

    Zoezi\(\PageIndex{2}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{3 x+y=5} \\ {2 x-3 y=7}\end{array}\right.\)

    Jibu

    (2,1-1)

    Zoezi\(\PageIndex{3}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{4 x+y=-5} \\ {-2 x-2 y=-2}\end{array}\right.\)

    Jibu

    (-2,3)

    Hatua zimeorodheshwa hapa chini kwa kumbukumbu rahisi.

    JINSI YA KUTATUA MFUMO WA EQUATIONS KWA KUONDOA.
    1. Andika equations zote mbili kwa fomu ya kawaida. Ikiwa coefficients yoyote ni sehemu ndogo, wazi.
    2. Fanya coefficients ya kinyume kimoja cha kutofautiana.
      • Chagua ni variable gani utaondoa.
      • Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume.
    3. Ongeza milinganyo inayotokana na Hatua ya 2 ili kuondoa variable moja.
    4. Tatua kwa kutofautiana iliyobaki.
    5. Badilisha suluhisho kutoka Hatua ya 4 kwenye moja ya milinganyo ya awali. Kisha kutatua kwa variable nyingine.
    6. Andika suluhisho kama jozi iliyoamriwa.
    7. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.

    Kwanza tutafanya mfano ambapo tunaweza kuondoa variable moja mara moja.

    Zoezi\(\PageIndex{4}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{x+y=10} \\ {x-y=12}\end{array}\right.\)

    Jibu
      .
    Equations zote mbili ziko katika fomu ya kawaida.  
    Coefficients ya y tayari ni kinyume.  
    Ongeza equations mbili ili kuondoa y.
    Equation kusababisha ina tu 1 variable, x.    		 .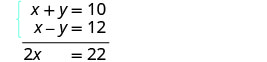
    Kutatua kwa x, variable iliyobaki.

    Mbadala x = 11 katika moja ya milinganyo ya awali.    		 .
      .
    Kutatua kwa variable nyingine, y. .
    Andika suluhisho kama jozi iliyoamriwa. Jozi iliyoamriwa ni (11, -1).
    Angalia kwamba jozi iliyoamriwa ni suluhisho la
    equations zote za awali.

    \(\begin{array}{rllrll} x+y &=&10 &x-y&=&12\\ 11+(-1) &\stackrel{?}{=}&10 & 11-(-1) &\stackrel{?}{=}&12\\ 10 &=&10 \checkmark & 12 &=&12 \checkmark \end{array}\)    		  
      Suluhisho ni (11, -1).
    Zoezi\(\PageIndex{5}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{2 x+y=5} \\ {x-y=4}\end{array}\right.\)

    Jibu

    (3, -1)

    Zoezi\(\PageIndex{6}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{x+y=3} \\ {-2 x-y=-1}\end{array}\right.\)

    Jibu

    (-2,5)

    Katika Zoezi\(\PageIndex{7}\), tutaweza kufanya coefficients ya kupinga moja kutofautiana kwa kuzidisha equation moja kwa mara.

    Zoezi\(\PageIndex{7}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{3 x-2 y=-2} \\ {5 x-6 y=10}\end{array}\right.\)

    Jibu
      .
    Equations zote mbili ziko katika fomu ya kawaida.  
    Hakuna hata coefficients ni kinyume.  
    Tunaweza kufanya coefficients ya kupinga y kwa kuzidisha equation
    ya kwanza kwa -3.    		 .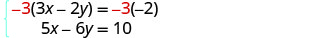
    Kurahisisha. .
    Ongeza equations mbili ili kuondoa y. .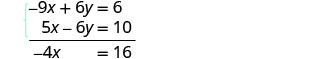
    Tatua kwa kutofautiana iliyobaki, x.
    Mbadala x = -4 katika moja ya milinganyo ya awali.    		 .
      .
    Kutatua kwa y. .
    .
    .
    Andika suluhisho kama jozi iliyoamriwa. Jozi zilizoamriwa ni (-4, -5).
    Angalia kwamba jozi iliyoamriwa ni suluhisho la equations
    zote za awali.

    \(\begin{array}{rllrll} 3x-2y &=&-2 &5x-6y&=&10\\ 3(-4)-2(-5) &\stackrel{?}{=}&-2 & 5(-4)-6(-5) &\stackrel{?}{=}&10\\ -12+10&\stackrel{?}{=}&-2 &-20+30&\stackrel{?}{=}&10\\-2 &=&-2 \checkmark & 10 &=&10 \checkmark \end{array}\)    		  
      Suluhisho ni (-4, -5).
    Zoezi\(\PageIndex{8}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{4 x-3 y=1} \\ {5 x-9 y=-4}\end{array}\right.\)

    Jibu

    (1,1)

    Zoezi\(\PageIndex{9}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{3 x+2 y=2} \\ {6 x+5 y=8}\end{array}\right.\)

    Jibu

    (-2,4)

    Sasa tutafanya mfano ambapo tunahitaji kuzidisha equations wote kwa constants ili kufanya coefficients ya kinyume variable moja.

    Zoezi\(\PageIndex{10}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{4 x-3 y=9} \\ {7 x+2 y=-6}\end{array}\right.\)

    Jibu

    Katika mfano huu, hatuwezi kuzidisha equation moja tu na mara kwa mara yoyote kupata coefficients kinyume. Hivyo sisi kimkakati kuzidisha equations wote na mara kwa mara kupata kupinga.

      .
    Equations zote mbili ziko katika fomu ya kawaida. Ili kupata
    coefficients kinyume cha y, tutazidisha equation ya kwanza na 2
    na equation ya pili na 3.    		 .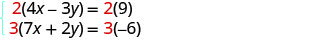
    Kurahisisha. .
    Ongeza equations mbili ili kuondoa y. .
    Kutatua kwa x.

    Mbadala x = 0 katika moja ya milinganyo ya awali.    		 .
      .
    Kutatua kwa y. .
      .
    Andika suluhisho kama jozi iliyoamriwa. Jozi iliyoamriwa ni (0, -3).
    Angalia kwamba jozi iliyoamriwa ni suluhisho la equations
    zote za awali.

    \(\begin{array}{rllrll} 4x-3y &=&9 &7x+2y&=&-6\\ 4(0)-3(-3) &\stackrel{?}{=}&9 & 7(0)+2(-3) &\stackrel{?}{=}&-6\\9 &=&9 \checkmark & -6 &=&-6 \checkmark \end{array}\)    		  
      Suluhisho ni (0, -3).
    Zoezi\(\PageIndex{11}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.\)

    Jibu

    (1,3)

    Zoezi\(\PageIndex{12}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{7 x+8 y=4} \\ {3 x-5 y=27}\end{array}\right.\)

    Jibu

    (4, 1-3)

    Wakati mfumo wa equations una sehemu ndogo, tutaanza kufuta sehemu ndogo kwa kuzidisha kila equation na LCD yake.

    Zoezi\(\PageIndex{13}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{x+\frac{1}{2} y=6} \\ {\frac{3}{2} x+\frac{2}{3} y=\frac{17}{2}}\end{array}\right.\)

    Jibu

    Katika mfano huu, equations zote mbili zina sehemu ndogo. Hatua yetu ya kwanza itakuwa kuzidisha kila equation na LCD yake ya wazi FRACTIONS.

      .
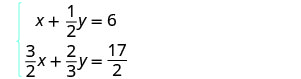
    Ili kufuta sehemu ndogo, kuzidisha kila equation na LCD yake. .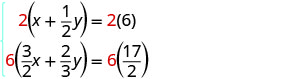
    Kurahisisha. .
    Sasa tuko tayari kuondokana na moja ya vigezo. Kumbuka kwamba equations
    wote ni katika hali ya kawaida.    		  
    Tunaweza kuondoa y kuzidisha equation ya juu kwa -4. .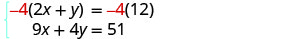
    Kurahisisha na kuongeza.



    Mbadala x = 3 katika moja ya milinganyo ya awali.    		 .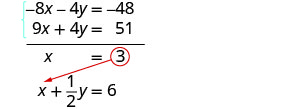
    Kutatua kwa y. .
      .
      .
    Andika suluhisho kama jozi iliyoamriwa. Jozi iliyoamriwa ni (3, 6).
    Angalia kwamba jozi iliyoamriwa ni suluhisho la
    equations zote za awali.

    \(\begin{array}{rllrll} x+\frac{1}{2}y &=&6 &\frac{3}{2}x+\frac{2}{3}y&=&\frac{17}{2}\\ 3+\frac{1}{2}(6) &\stackrel{?}{=}&6 &\frac{3}{2}(3) + \frac{2}{3}(6)&\stackrel{?}{=}&\frac{17}{2}\\ 3 + 3 &\stackrel{?}{=}&6 & \frac{9}{2 }+4 &\stackrel{?}{=} & \frac{17}{2}\\ 6 &=&6 \checkmark & \frac{9}{2} + \frac{8}{2} &\stackrel{?}{=} & \frac{17}{2}\\ && & \frac{17}{2} &=&\frac{17}{2} \checkmark \end{array}\)    		  
      Suluhisho ni (3, 6).
    Zoezi\(\PageIndex{14}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{\frac{1}{3} x-\frac{1}{2} y=1} \\ {\frac{3}{4} x-y=\frac{5}{2}}\end{array}\right.\)

    Jibu

    (6,2)

    Zoezi\(\PageIndex{15}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{x+\frac{3}{5} y=-\frac{1}{5}} \\ {-\frac{1}{2} x-\frac{2}{3} y=\frac{5}{6}}\end{array}\right.\)

    Jibu

    (1, -2)

    Katika Mifumo ya Kutatua ya Equations kwa Graphing tuliona kwamba sio mifumo yote ya equations linear ina jozi moja iliyoamriwa kama suluhisho. Wakati equations mbili zilikuwa mstari sawa, kulikuwa na ufumbuzi mkubwa sana. Sisi kuitwa kwamba mfumo thabiti. Wakati equations mbili ilivyoelezwa mistari sambamba, hapakuwa na ufumbuzi. Sisi kuitwa kwamba mfumo haiendani.

    Zoezi\(\PageIndex{16}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{3 x+4 y=12} \\ {y=3-\frac{3}{4} x}\end{array}\right.\)

    Jibu

    \(\begin{array} {ll} & \left\{\begin{aligned} 3 x+4 y &=12 \\ y &=3-\frac{3}{4} x \end{aligned}\right. \\\\\text{Write the second equation in standard form.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {\frac{3}{4} x+y=3}\end{array}\right.\\ \\ \text{Clear the fractions by multiplying thesecond equation by 4.} & \left\{\begin{aligned} 3 x+4 y &=12 \\ 4\left(\frac{3}{4} x+y\right) &=4(3) \end{aligned}\right. \\\\ \text{Simplify.} & \left\{\begin{array}{l}{3 x+4 y=12} \\ {3 x+4 y=12}\end{array}\right.\\\\ \text{To eliminate a variable, we multiply thesecond equation by −1.} & \left\{\begin{array}{c}{3 x+4 y=12} \\ \underline{-3 x-4 y=-12} \end{array}\right.\\ &\qquad\qquad\quad 0=0 \\ \text{Simplify and add.} \end{array}\)

    Hii ni kauli ya kweli. Equations ni thabiti lakini tegemezi. Grafu zao zitakuwa mstari sawa. Mfumo una ufumbuzi mkubwa sana.

    Baada ya kufuta sehemu ndogo katika equation ya pili, je, umeona kwamba equations mbili zilikuwa sawa? Hiyo ina maana tuna mistari coincident.

    Zoezi\(\PageIndex{17}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{5 x-3 y=15} \\ {y=-5+\frac{5}{3} x}\end{array}\right.\)

    Jibu

    ufumbuzi mkubwa sana

    Zoezi\(\PageIndex{18}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{x+2 y=6} \\ {y=-\frac{1}{2} x+3}\end{array}\right.\)

    Jibu

    ufumbuzi mkubwa sana

    Zoezi\(\PageIndex{19}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{-6 x+15 y=10} \\ {2 x-5 y=-5}\end{array}\right.\)

    Jibu

    \(\begin{array} {ll} \text{The equations are in standard form.}& \left\{\begin{aligned}-6 x+15 y &=10 \\ 2 x-5 y &=-5 \end{aligned}\right. \\\\ \text{Multiply the second equation by 3 to eliminate a variable.} & \left\{\begin{array}{l}{-6 x+15 y=10} \\ {3(2 x-5 y)=3(-5)}\end{array}\right. \\\\ \text{Simplify and add.} & \left\{\begin{aligned}{-6 x+15 y =10} \\ \underline{6 x-15 y =-15} \end{aligned}\right. \\ & \qquad \qquad \quad0\neq 5 \end{array}\)

    Kauli hii ni ya uongo. equations ni haiendani na hivyo grafu zao itakuwa mistari sambamba.

    Mfumo hauna suluhisho.

    Zoezi\(\PageIndex{20}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{-3 x+2 y=8} \\ {9 x-6 y=13}\end{array}\right.\)

    Jibu

    hakuna suluhisho

    Zoezi\(\PageIndex{21}\)

    Tatua mfumo kwa kuondoa. \(\left\{\begin{array}{l}{7 x-3 y=-2} \\ {-14 x+6 y=8}\end{array}\right.\)

    Jibu

    hakuna suluhisho

    Kutatua Matumizi ya Mifumo ya Equations na Kuondoa

    Baadhi ya matatizo ya programu hutafsiri moja kwa moja kwenye usawa katika fomu ya kawaida, kwa hiyo tutatumia njia ya kuondoa ili kutatua. Kama hapo awali, tunatumia Mkakati wetu wa kutatua matatizo ili kutusaidia kukaa umakini na kupangwa.

    Zoezi\(\PageIndex{22}\)

    Jumla ya namba mbili ni 39. Tofauti yao ni 9. Kupata idadi.

    Jibu

    \(\begin{array} {ll} \textbf{Step 1. Read}\text{ the problem}& \\ \textbf{Step 2. Identify} \text{ what we are looking for.} & \text{We are looking for two numbers.} \\\textbf{Step 3. Name} \text{ what we are looking for.} & \text{Let n = the first number.} \\ & \text{ m = the second number} \\\textbf{Step 4. Translate} \text{ into a system of equations.}& \\ & \text{The sum of two numbers is 39.} \\ & n+m=39\\ & \text{Their difference is 9.} \\ & n−m=9 \\ \\ \text{The system is:} & \left\{\begin{array}{l}{n+m=39} \\ {n-m=9}\end{array}\right. \\\\ \textbf{Step 5. Solve} \text{ the system of equations. } & \\ \text{To solve the system of equations, use} \\ \text{elimination. The equations are in standard} \\ \text{form and the coefficients of m are} & \\ \text{opposites. Add.} & \left\{\begin{array}{l}{n+m=39} \\ \underline{n-m=9}\end{array}\right. \\ &\quad 2n\qquad=48 \\ \\\text{Solve for n.} & n=24 \\ \\ \text{Substitute n=24 into one of the original} &n+m=39 \\ \text{equations and solve form.} & 24+m=39 \\ & m=15 \\ \textbf{Step 6. Check}\text{ the answer.} & \text{Since 24+15=39 and 24−15=9, the answers check.}\\ \textbf{Step 7. Answer} \text{ the question.} & \text{The numbers are 24 and 15.} \end{array}\)

    Zoezi\(\PageIndex{23}\)

    Jumla ya namba mbili ni 42. Tofauti yao ni 8. Kupata idadi.

    Jibu

    Idadi ni 25 na 17.

    Zoezi\(\PageIndex{24}\)

    Jumla ya namba mbili ni -15. Tofauti yao ni -35. Kupata idadi.

    Jibu

    Nambari ni -25 na 10.

    Zoezi\(\PageIndex{25}\)

    Joe ataacha kwenye mgahawa wa Burger kila siku akiwa njiani kwenda kufanya kazi. Jumatatu alikuwa na amri moja ya fries kati na soda mbili ndogo, ambayo ilikuwa na jumla ya kalori 620. Jumanne alikuwa na amri mbili za fries kati na soda moja ndogo, kwa jumla ya kalori 820. Kuna kalori ngapi katika utaratibu mmoja wa fries kati? Ni kalori ngapi katika soda moja ndogo?

    Jibu
    Hatua ya 1. Soma tatizo.  
    Hatua ya 2. Tambua kile tunachotafuta. Tunatafuta idadi ya
    kalori kwa utaratibu mmoja wa fries kati
    na katika soda moja ndogo.
    Hatua ya 3. Jina kile tunachotafuta. Hebu f = idadi ya kalori katika utaratibu
    1 wa fries kati.
    s = idadi ya kalori katika soda
    1 ndogo.
    Hatua ya 4. Tafsiri katika mfumo wa equations: moja kati fries na soda mbili ndogo alikuwa na
    jumla ya kalori 620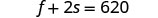
      .
      fries mbili kati na moja ndogo soda alikuwa na
    jumla ya kalori 820.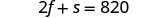
      .
    Mfumo wetu ni: .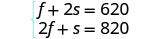
    Hatua ya 5. Tatua mfumo wa equations.
    Ili kutatua mfumo wa equations, tumia
    kuondoa. Equations ni katika
    fomu ya kawaida. Ili kupata coefficients kinyume cha f,
    kuzidisha equation ya juu na -1.    		 .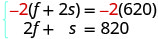
    Kurahisisha na kuongeza. .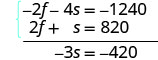
    Kutatua kwa s. .
    Mbadala s = 140 katika moja ya
    milinganyo ya awali na kisha kutatua kwa f.    		 .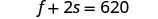
      .
      .
      .
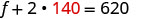
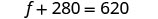
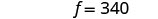
    Hatua ya 6. Angalia jibu. Thibitisha kwamba namba hizi zina maana
    katika tatizo na kwamba ni
    ufumbuzi wa equations zote mbili.
    Tunakuacha hii kwako!
    Hatua ya 7. Jibu swali. Soda ndogo ina kalori 140 na
    fries zina kalori 340.
    Zoezi\(\PageIndex{26}\)

    Malik ataacha kwenye duka la vyakula ili kununua mfuko wa diapers na makopo 2 ya formula. Anatumia jumla ya $37. Wiki ijayo anaacha na kununua mifuko 2 ya diapers na makopo 5 ya formula kwa jumla ya $87. Je! Mfuko wa diapers una gharama gani? Ni kiasi gani kinachoweza moja ya formula?

    Jibu

    Mfuko wa diapers gharama $11 na uwezo wa formula gharama $13.

    Zoezi\(\PageIndex{27}\)

    Ili kupata ulaji wake wa kila siku wa matunda kwa siku, Sasha anakula ndizi na jordgubbar 8 Jumatano kwa hesabu ya kalori ya 145. Jumatano iliyofuata, anakula ndizi mbili na jordgubbar 5 kwa jumla ya kalori 235 kwa matunda. Kuna kalori ngapi katika ndizi? Ni kalori ngapi katika strawberry?

    Jibu

    Kuna kalori 105 katika ndizi na kalori 5 katika strawberry.

    Chagua Njia rahisi zaidi ya Kutatua Mfumo wa Ulinganisho wa Mstari

    Wakati utakuwa na kutatua mfumo wa equations linear katika darasa baadaye math, wewe kawaida si kuambiwa ambayo njia ya kutumia. Utahitaji kufanya uamuzi huo mwenyewe. Kwa hivyo utahitaji kuchagua njia ambayo ni rahisi kufanya na kupunguza nafasi yako ya kufanya makosa.

    Jedwali hili lina safu mbili na nguzo tatu. Mstari wa kwanza unaandika nguzo kama “Graphing,” “Kubadilisha,” na “Kuondoa.” Chini ya “Graphing” inasema, “Tumia wakati unahitaji picha ya hali hiyo.” Chini ya “Badala” inasema, “Tumia wakati equation moja tayari kutatuliwa kwa variable moja.” Chini ya “Kutokomeza” inasema, “Tumia wakati equations iko katika fomu ya kawaida.”

    Zoezi\(\PageIndex{28}\)

    Kwa kila mfumo wa equations linear kuamua kama itakuwa rahisi zaidi kutatua kwa kubadilisha au kuondoa. Eleza jibu lako.

    1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)
    Jibu

    1. \(\left\{\begin{array}{l}{3 x+8 y=40} \\ {7 x-4 y=-32}\end{array}\right.\)

    Kwa kuwa equations zote mbili ziko katika fomu ya kawaida, kutumia kuondoa itakuwa rahisi zaidi.

    2. \(\left\{\begin{array}{l}{5 x+6 y=12} \\ {y=\frac{2}{3} x-1}\end{array}\right.\)

    Kwa kuwa equation moja tayari kutatuliwa kwa y, kutumia badala itakuwa rahisi zaidi.

    Zoezi\(\PageIndex{29}\)

    Kwa kila mfumo wa equations linear, kuamua kama itakuwa rahisi zaidi kutatua kwa kubadilisha au kuondoa. Eleza jibu lako.

    1. \(\left\{\begin{array}{l}{4 x-5 y=-32} \\ {3 x+2 y=-1}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{x=2 y-1} \\ {3 x-5 y=-7}\end{array}\right.\)
    Jibu
    1. Kwa kuwa equations zote mbili ziko katika fomu ya kawaida, kutumia kuondoa itakuwa rahisi zaidi.
    2. Kwa kuwa equation moja tayari kutatuliwa kwa xx, kutumia badala itakuwa rahisi zaidi.
    Zoezi\(\PageIndex{30}\)

    Kwa kila mfumo wa equations linear, kuamua kama itakuwa rahisi zaidi kutatua kwa kubadilisha au kuondoa. Eleza jibu lako.

    1. \(\left\{\begin{array}{l}{y=2 x-1} \\ {3 x-4 y=-6}\end{array}\right.\)
    2. \(\left\{\begin{array}{l}{6 x-2 y=12} \\ {3 x+7 y=-13}\end{array}\right.\)
    Jibu
    1. Kwa kuwa equation moja tayari kutatuliwa kwa yy, kutumia badala itakuwa rahisi zaidi;
    2. Kwa kuwa equations zote mbili ziko katika fomu ya kawaida, kutumia kuondoa itakuwa rahisi zaidi.
    Kumbuka

    Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na mifumo ya kutatua ya usawa wa mstari kwa kuondoa.

    Dhana muhimu

    • Kutatua Mfumo wa Equations kwa Kuondoa
      1. Andika equations zote mbili kwa fomu ya kawaida. Ikiwa coefficients yoyote ni sehemu ndogo, wazi.
      2. Fanya coefficients ya kinyume kimoja cha kutofautiana.
        • Chagua ni variable gani utaondoa.
        • Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume.
      3. Ongeza milinganyo inayotokana na Hatua ya 2 ili kuondoa variable moja.
      4. Tatua kwa kutofautiana iliyobaki.
      5. Badilisha suluhisho kutoka Hatua ya 4 kwenye moja ya milinganyo ya awali. Kisha kutatua kwa variable nyingine.
      6. Andika suluhisho kama jozi iliyoamriwa.
      7. Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.