1.10: Mali ya Hesabu halisi
- Page ID
- 178034
Mwishoni mwa sehemu hii, utaweza:
- Tumia mali za kubadilisha na za ushirika
- Tumia utambulisho na mali inverse ya kuongeza na kuzidisha
- Tumia mali ya sifuri
- Kurahisisha maneno kwa kutumia mali ya kusambaza
Utangulizi wa kina zaidi wa mada yaliyofunikwa katika sehemu hii inaweza kupatikana katika sura ya Prealgebra, Mali ya Hesabu halisi.
Tumia Mali za Comutative na Associative
Fikiria juu ya kuongeza namba mbili, sema 5 na 3. Ili sisi kuongeza yao haiathiri matokeo, je, ni?
\[\begin{array} { cc } { 5 + 3 } & { 3 + 5 } \\ { 8 } & { 8 } \\ { 5 + 3 = } & { 3 + 5 } \end{array}\]
Matokeo ni sawa.
Kama tunaweza kuona, utaratibu ambao tunaongeza haijalishi!
Nini kuhusu kuzidisha 5 na 3?
\[\begin{array} { c c } { 5 \cdot 3 } & { 3 \cdot 5 } \\ { 15 } & { 15 } \\ { 5 \cdot 3=} &{3 \cdot 5 } \end{array}\]
Tena, matokeo ni sawa!
Utaratibu ambao tunazidisha haijalishi!
Mifano hii kuonyesha mali commutative. Wakati wa kuongeza au kuzidisha, kubadilisha utaratibu hutoa matokeo sawa.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b \text { are real numbers, then } \quad a + b = b + a } \\ { \textbf { of Multiplication } } & { \text { If } a , b \text { are real numbers, then } \quad a \cdot b = b \cdot a } \end{array}\]
Wakati wa kuongeza au kuzidisha, kubadilisha utaratibu hutoa matokeo sawa.
Mali ya kubadilisha inahusiana na utaratibu. Ikiwa unabadilisha utaratibu wa namba wakati wa kuongeza au kuzidisha, matokeo ni sawa.
Nini kuhusu kuondoa? Je, ili jambo wakati sisi Ondoa idadi? Je, 71-3 hutoa matokeo sawa na 3—7?
\[\begin{array} { c c } { 7 - 3 } & { 3 - 7 } \\ { 4 } & { - 4 } \end{array}\]
\[\begin{aligned} 4 & \neq - 4 \\ 7 - 3 & \neq 3 - 7 \end{aligned}\]
Matokeo si sawa.
Kwa kuwa kubadilisha utaratibu wa uondoaji haukutoa matokeo sawa, tunajua kwamba uondoaji sio kubadilisha.
Hebu tuone kinachotokea tunapogawanya namba mbili. Je mgawanyiko commutative?
\[\begin{array} { cc} { 12 \div 4 } & { 4 \div 12 } \\ { \frac { 12 } { 4 } } & { \frac { 4 } { 12 } } \\ { 3 } & { \frac { 1 } { 3 } } \end{array}\]
\[\begin{aligned} 3 \neq & \frac { 1 } { 3 } \\ 12 \div 4 & \neq 4 \div 12 \end{aligned}\]
Matokeo si sawa.
Kwa kuwa kubadilisha utaratibu wa mgawanyiko haukutoa matokeo sawa, mgawanyiko hauwezi kubadilisha. Mali ya kubadilisha hutumika tu kwa kuongeza na kuzidisha!
- Kuongezea na kuzidisha ni commutative.
- Ondoa na Idara si commutative.
Ikiwa uliulizwa kurahisisha maneno haya, ungefanyaje na jibu lako lingekuwa nini?
\[7 + 8 + 2\]
Baadhi ya watu kufikiri\(7+8\) ni 15 na kisha\(15+2\) ni 17. Wengine wanaweza kuanza na\(8+2\) hufanya 10 na kisha\(7+10\) hufanya 17.
Njia yoyote inatoa matokeo sawa. Kumbuka, tunatumia mabano kama alama za makundi ili kuonyesha operesheni ipi inapaswa kufanyika kwanza.
\[\begin{array} { ll } { \text{ Add } 7 + 8 . } & { ( 7 + 8 ) + 2 } \\ { \text { Add. } } & { 15 + 2 } \\ { \text { Add. } } & { 17 } \\ \\ { } & { 7 + ( 8 + 2 ) } \\ { \text { Add } 8 + 2 . } & { 7 + 10 } \\ { \text { Add. } } & { 77 } \\\\ { ( 7 + 8 ) + 2 = 7 + ( 8 + 2 ) } \end{array}\]
Wakati wa kuongeza namba tatu, kubadilisha kikundi cha namba hutoa matokeo sawa.
Hii ni kweli kwa kuzidisha, pia.
\[\begin{array} { ll } { } & { (5\cdot \frac{1}{3})\cdot 3 } \\ { \text { Multiply. } 5\cdot \frac{1}{3} } & { \frac{5}{3}\cdot 3 } \\ { \text { Multiply. } } & { 5 } \\ \\ { } & { 5\cdot (\frac{1}{3}\cdot 3) } \\ { \text { Multiply. } \frac{1}{3}\cdot 3 } & { 5\cdot 1 } \\ { \text { Multiply. } } & { 5 } \\ \\ { (5\cdot \frac{1}{3})\cdot 3 = 5\cdot (\frac{1}{3}\cdot 3) } \end{array}\]
Wakati wa kuzidisha namba tatu, kubadilisha kikundi cha namba hutoa matokeo sawa.
Labda unajua hili, lakini istilahi inaweza kuwa mpya kwako. Mifano hii inaonyesha mali associative.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b , c \text { are real numbers, then } ( a + b ) + c = a + ( b + c ) } \\ { \textbf { of Multiplication } } & { \text { If } a , b , c \text { are real numbers, then } ( a \cdot b ) \cdot c = a \cdot ( b \cdot c ) } \end{array}\]
Wakati wa kuongeza au kuzidisha, kubadilisha kikundi hutoa matokeo sawa.
Hebu fikiria tena juu ya kuzidisha\(5\cdot \frac{1}{3}\cdot 3\). Tulipata matokeo sawa kwa njia zote mbili, lakini njia ipi ilikuwa rahisi? Kuzidisha\(\frac{1}{3}\) na 3 kwanza, kama inavyoonyeshwa hapo juu upande wa kulia, hupunguza sehemu katika hatua ya kwanza. Kutumia mali associative unaweza kufanya hesabu rahisi!
Mali ya ushirika inahusiana na kikundi. Ikiwa tunabadilisha jinsi namba zilivyowekwa, matokeo yatakuwa sawa. Taarifa ni sawa namba tatu katika utaratibu sawa-tofauti tu ni kambi.
Tuliona kwamba uondoaji na mgawanyiko haukuwa wa kubadilisha. Wao si associative aidha.
Wakati wa kurahisisha maneno, daima ni wazo nzuri kupanga mipango gani itakuwa. Ili kuchanganya maneno kama hayo katika mfano unaofuata, tutatumia mali ya kubadilisha ya kuongeza kuandika maneno kama hayo pamoja.
Kurahisisha:\(18p+6q+15p+5q\).
- Jibu
-
\[\begin{array} { l l} {} &{18p+6q+15p+5q}\\ \\{ \text { Use the commutative property of addition } } &{} \\ { \text {to re-order so that like terms are together.} } &{18p+15p+ 6q+5q} \\ \\ {\text{Add like terms.}} &{33p + 11q} \end{array}\]
Kurahisisha:\(23r+14s+9r+15s\).
- Jibu
-
\(32r+29s\)
Kurahisisha:\(37m+21n+4m−15n\).
- Jibu
-
\(41m+6n\)
Wakati tuna kurahisisha algebraic kujieleza s, tunaweza mara nyingi kufanya kazi rahisi kwa kutumia commutative au associative mali kwanza, badala ya moja kwa moja kufuata utaratibu wa shughuli. Wakati wa kuongeza au kuondoa sehemu ndogo, kuchanganya wale walio na denominator ya kawaida kwanza.
Kurahisisha:\((\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}\)
- Jibu
-
\[\begin{array} { l l } {} &{(\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}} \\{ \text { Notice that the last } 2 \text { terms have a } } \\ { \text { common denominator, so change the } } &{\frac { 5 } { 13 } + \left( \frac { 3 } { 4 } + \frac { 1 } { 4 } \right)}\\ { \text { grouping. } } &{}\\ \\ {\text{Add in parentheses first.}} &{\frac{5}{13} + (\frac{4}{4})} \\ \\ {\text{Simplify the fraction.}} &{\frac{5}{13} + 1} \\ \\ {\text{Add.}} &{1\frac{5}{13}} \\ \\ {\text{Convert to an improper fraction.}} &{\frac{18}{13}} \end{array}\]
Kurahisisha:\((\frac{7}{15} + \frac{5}{8}) + \frac{3}{8}\)
- Jibu
-
\(1\frac{7}{15}\)
Kurahisisha:\((\frac{2}{9} + \frac{7}{12}) + \frac{5}{12}\)
- Jibu
-
\(1\frac{2}{9}\)
Tumia mali ya ushirika ili kurahisisha\(6(3x)\).
- Jibu
-
Tumia mali ya ushirika wa kuzidisha\((a\cdot b)\cdot c=a\cdot (b\cdot c)\),, kubadili kikundi.
\[\begin{array} { ll } {} &{ 6 ( 3 x ) } \\ { \text { Change the grouping. } } &{(6\cdot 3)x} \\ { \text { Multiply in the parentheses. } } &{18} \end{array}\]
Kumbuka kwamba tunaweza kuzidisha\(6\cdot 3\) lakini hatukuweza kuzidisha\(3x\) bila kuwa na thamani ya\(x\).
Tumia mali ya ushirika ili kurahisisha\(8(4x)\).
- Jibu
-
\(32x\)
Tumia mali ya ushirika ili kurahisisha\(-9(7y)\).
- Jibu
-
\(-63y\)
Tumia Utambulisho na Mali ya Inverse ya Kuongeza na Kuzidisha
Nini kinatokea wakati sisi kuongeza 0 kwa idadi yoyote? Kuongeza 0 haina mabadiliko ya thamani. Kwa sababu hii, tunaita 0 utambulisho wa kuongezea.
Kwa mfano,
\[\begin{array} { c c c } { 13 + 0 } & { - 14 + 0 } & { 0 + ( - 8 ) } \\ { 13 } & { - 14 } & { - 8 } \end{array}\]
Mifano hii kuonyesha Identity Mali ya Aidha kwamba inasema kwamba kwa idadi yoyote halisi\(a\),\(a+0=a\) na\(0+a=a\).
Nini kinatokea wakati sisi kuzidisha idadi yoyote kwa moja? Kuongezeka kwa 1 haina mabadiliko ya thamani. Hivyo tunaita 1 utambulisho multiplicative.
Kwa mfano,\[\begin{array} { r r r } { 43 \cdot 1 } & { - 27 \cdot 1 } & { 1 \cdot \frac { 3 } { 5 } } \\ { 43 } & { - 27 } & { \frac { 3 } { 5 } } \end{array}\]
Mifano hii kuonyesha Identity Mali ya Kuzidisha kwamba inasema kwamba kwa idadi yoyote halisi\(a\),\(a\cdot 1=a\) na\(1\cdot a=a\).
Sisi muhtasari Mali Identity chini.
\[\begin{array} { l l} { \textbf {of addition}\text{ For any real number } a : } &{ a + 0 = a \quad 0 + a = a } \\ { \textbf{0} \text { is the}\textbf{ additive identity } } \\ {\textbf {of multiplication}\text{ For any real number } a : } &{ a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1}\text{ is the}\textbf{ multiplicative identity } } \end{array}\]

Angalia kwamba katika kila kesi, idadi ya kukosa ilikuwa kinyume na idadi!
sisi\(−a\) kuwaita. livsmedelstillsats inverse ya. Kinyume cha nambari ni inverse yake ya kuongezea. Nambari na kinyume chake huongeza sifuri, ambayo ni utambulisho wa kuongezea. Hii inasababisha Inverse Mali ya Aidha kwamba inasema kwa idadi yoyote halisi\(a, a+(−a)=0\). Kumbuka, idadi na kinyume chake huongeza sifuri.
Nini idadi tele na\(\frac{2}{3}\) anatoa utambulisho multiplicative, 1? Kwa maneno mengine,\(\frac{2}{3}\) mara nini matokeo katika 1?

Nambari gani imeongezeka kwa 2 inatoa utambulisho wa kuzidisha, 1? Kwa maneno mengine, mara 2 ni matokeo gani katika 1?

Angalia kwamba katika kila kesi, nambari iliyopo ilikuwa ya kawaida ya idadi!
Tunatoa\(\frac{1}{a}\) wito inverse multiplicative ya. Utoaji wa nambari ni inverse yake ya kuzidisha. Nambari na kuongezeka kwake kwa moja, ambayo ni utambulisho wa kuzidisha. Hii inasababisha Mali Inverse ya Kuzidisha ambayo inasema kwamba kwa idadi yoyote halisi\(a, a\neq 0, a\cdot \frac{1}{a}=1\).
Tutaweza rasmi hali mali inverse hapa:
\[\begin{array} { l l l } { \textbf { of addition } } &{ \text { For any real number } a,} &{a + (-a) = 0}\\{} &{-a \text{. is the}\textbf{ additive inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its opposite add to zero. } }&{}\\ \\{ \textbf { of multiplication } } &{ \text { For any real number } a, a\neq 0} &{a\cdot \frac{1}{a} = 1}\\{} &{\frac{1}{a} \text{. is the}\textbf{ multiplicative inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its reciprocal multiply to zero. } }&{} \end{array}\]
Kupata inverse livsmedelstillsats
- \(\frac{5}{8}\)
- \(0.6\)
- \(-8\)
- \(-\frac{4}{3}\)
- Jibu
-
Ili kupata inverse ya kuongezea, tunapata kinyume.
- Inverse ya kuongezea\(\frac{5}{8}\) ni kinyume cha\(\frac{5}{8}\). Inverse ya nyongeza ya\(\frac{5}{8}\) ni\(-\frac{5}{8}\)
- Inverse ya kuongezea\(0.6\) ni kinyume cha\(0.6\). Inverse ya nyongeza ya\(0.6\) ni\(-0.6\).
- Inverse ya kuongezea\(-8\) ni kinyume cha\(-8\). Sisi kuandika kinyume cha\(-8\) kama\(-(-8)\), na kisha kurahisisha kwa\(8\). Kwa hiyo, inverse ya nyongeza ya\(-8\) ni\(8\).
- Inverse ya kuongezea\(-\frac{4}{3}\) ni kinyume cha\(-\frac{4}{3}\). Tunaandika hii kama\(-(-\frac{4}{3})\), na kisha kurahisisha\(\frac{4}{3}\). Hivyo, inverse livsmedelstillsats ya\(-\frac{4}{3}\) ni\(\frac{4}{3}\).
Kupata inverse livsmedelstillsats
- \(\frac{7}{9}\)
- \(1.2\)
- \(-14\)
- \(-\frac{9}{4}\)
- Jibu
-
- \(-\frac{7}{9}\)
- \(-1.2\)
- \(14\)
- \(\frac{9}{4}\)
Kupata inverse livsmedelstillsats
- \(\frac{7}{13}\)
- \(8.4\)
- \(-46\)
- \(-\frac{5}{2}\)
- Jibu
-
- \(-\frac{7}{13}\)
- \(-8.4\)
- \(46\)
- \(\frac{5}{2}\)
Kupata inverse multiplicative ya
- \(9\)
- \(-\frac{1}{9}\)
- \(0.9\)
- Jibu
-
Ili kupata inverse ya kuzidisha, tunapata usawa.
- Inverse multiplicative ya\(9\) ni usawa wa\(9\), ambayo ni\(\frac{1}{9}\). Kwa hiyo, inverse multiplicative ya\(9\) ni\(\frac{1}{9}\).
- Inverse multiplicative ya\(-\frac{1}{9}\) ni usawa wa\(-\frac{1}{9}\), ambayo ni\(−9\). Hivyo, inverse multiplicative ya\(-\frac{1}{9}\) ni\(-9\).
- Ili kupata inverse multiplicative ya\(0.9\), sisi kwanza kubadilisha\(0.9\) kwa sehemu,\(\frac{9}{10}\). Kisha tunapata usawa wa sehemu hiyo. Usawa wa\(\frac{9}{10}\) ni\(\frac{10}{9}\). Hivyo inverse multiplicative ya\(0.9\) ni\(\frac{10}{9}\).
Kupata inverse multiplicative ya
- \(4\)
- \(-\frac{1}{7}\)
- \(0.3\)
- Jibu
-
- \(\frac{1}{4}\)
- \(-7\)
- \(\frac{10}{3}\)
Kupata inverse multiplicative ya
- \(18\)
- \(-\frac{4}{5}\)
- \(0.6\)
- Jibu
-
- \(\frac{1}{18}\)
- \(-\frac{5}{4}\)
- \(\frac{5}{3}\)
Tumia Mali ya Zero
mali ya utambulisho wa kuongeza anasema kwamba wakati sisi kuongeza 0 kwa idadi yoyote, matokeo ni kwamba idadi sawa. Nini kinatokea wakati sisi kuzidisha idadi kwa 0? Kuongezeka kwa 0 hufanya bidhaa sawa na sifuri.
Kwa yoyote ya kweli idadi a.
\[a \cdot 0 = 0 \quad 0 \cdot a = 0\]
Bidhaa ya idadi yoyote halisi na 0 ni 0.
Nini kuhusu mgawanyiko kuwashirikisha sifuri? Ni nini\(0\div 3\)? Fikiria juu ya mfano halisi: Ikiwa hakuna cookies katika jar ya kuki na watu 3 watawashirikisha, ni vidakuzi ngapi ambavyo kila mtu hupata? Hakuna vidakuzi vya kushiriki, hivyo kila mtu anapata cookies 0. Hivyo,
\[0\div 3 = 0\]
Tunaweza kuangalia mgawanyiko na kuhusiana kuzidisha ukweli.
\[12 \div 6 = 2 \text { because } 2 \cdot 6 = 12\]
Hivyo tunajua\(0\div 3=0\) kwa sababu\(0\cdot 3=0\).
Kwa yoyote halisi idadi a, ila\(0, \frac{0}{a}=0\) na\(0\div a=0\).
Zero imegawanywa na idadi yoyote halisi isipokuwa sifuri ni sifuri.
Sasa fikiria juu ya kugawa na sifuri. Matokeo ya kugawanya 4 na 0 ni nini? Fikiria juu ya ukweli unaohusiana na kuzidisha:\(4\div 0=?\) njia\(?\cdot 0=4\). Je, kuna idadi kwamba tele kwa 0 anatoa 4? Kwa kuwa idadi yoyote halisi tele kwa 0 anatoa 0, hakuna idadi halisi ambayo inaweza kuzidishwa na 0 kupata 4.
Tunahitimisha kuwa hakuna jibu kwa\(4\div 0\) na hivyo tunasema kuwa mgawanyiko na 0 haujafafanuliwa.
Kwa yoyote halisi idadi a, ila\(0, \frac{a}{0}\) na\(a\div 0\) ni undefined.
Idara na sifuri haijulikani.
Sisi muhtasari mali ya sifuri chini.
Kuzidisha na Zero: Kwa yoyote ya kweli idadi a,
\[a \cdot 0 = 0 \quad 0 \cdot a = 0 \quad \text { The product of any number and } 0 \text { is } 0\]
Idara ya Zero, Idara na Zero: Kwa idadi yoyote halisi\(a, a\neq 0\)
\[\begin{array} { l l } { \frac { 0 } { a } = 0 } & { \text { Zero divided by any real number, except itself is zero. } } \\ { \frac { a } { 0 } \text { is undefined } } & { \text { Division by zero is undefined. } } \end{array}\]
Kurahisisha:
- \(-8\cdot 0\)
- \(\frac{0}{-2}\)
- \(\frac{-32}{0}\)
- Jibu
-
- \[\begin{array} { cc } { } &{-8\cdot 0}\\{\text{The product of any real number and 0 is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{0}{-2}}\\{\text{Zero divided by any real number, except}} &{} \\ {\text{itself, is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{-32}{0}}\\ {\text{Division by 0 is undefined.}} &{\text{undefined}} \end{array}\]
Kurahisisha:
- \(-14\cdot 0\)
- \(\frac{0}{-6}\)
- \(\frac{-2}{0}\)
- Jibu
-
- \(0\)
- \(0\)
- haijafafanuliwa
Kurahisisha:
- \(0(-17)\)
- \(\frac{0}{-10}\)
- \(\frac{-5}{0}\)
- Jibu
-
- \(0\)
- \(0\)
- haijafafanuliwa
Sasa tutatumia kutumia mali ya utambulisho, inverses, na sifuri ili kurahisisha maneno.
Kurahisisha:
- \(\frac{0}{n + 5}\), wapi\(n\neq −5\)
- \(\frac{10 - 3p}{0}\)wapi\(10 - 3p \neq 0\)
- Jibu
-
- \[\begin{array} { ll } { } &{\frac{0}{n + 5}}\\ {\text { Zero divided by any real number except }} &{0} \\ { \text { itself is } 0.} &{} \end{array}\]
- \[\begin{array} { ll } { } &{\frac{10 - 3p}{0}}\\ {\text { Division by 0 is undefined }} &{\text{undefined}} \end{array}\]
Kurahisisha:\(−84n+(−73n)+84n\).
- Jibu
-
\[\begin{array} { l l } { } &{−84n+(−73n)+84n} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { opposites; use the commutative property of } } &{- 84 n + 84 n + ( - 73 n ) } \\ { \text { addition to re-order the terms. } } &{} \\ \\ { \text { Add left to right. } } &{0 + (-73)}\\ \\{ \text { Add. } } &{-73n} \end{array}\]
Kurahisisha:\(−27a+(−48a)+27a\).
- Jibu
-
\(−48a\)
Kurahisisha:\(39x+(−92x)+(−39x)\).
- Jibu
-
\(−92x\)
Sasa tutaona jinsi kutambua usawa ni muhimu. Kabla ya kuzidisha kushoto kwenda kulia, angalia kurudisha-bidhaa zao ni 1.
Kurahisisha:\(\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}\)
- Jibu
-
\[\begin{array} { l l } { } &{\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { reciprocals, so use the commutative } } &{\frac{7}{15}\cdot\frac{15}{7}\cdot\frac{8}{23}} \\ { \text { property of multiplication to re-order the } } &{} \\ { \text { factors. } } &{}\\ \\{ \text { Multiply left to right. } } &{1\cdot\frac{8}{23}} \\\\{\text{Multiply.}} &{\frac{8}{23}}\end{array}\]
Kurahisisha:\(\frac{9}{16}\cdot\frac{5}{49}\cdot\frac{16}{9}\)
- Jibu
-
\(\frac{5}{49}\)
Kurahisisha:\(\frac{6}{17}\cdot\frac{11}{25}\cdot\frac{17}{6}\)
- Jibu
-
\(\frac{11}{25}\)
Kurahisisha:
- \(\frac{0}{m + 7}\), wapi\(m \neq -7\)
- \(\frac{18 - 6c}{0}\), wapi\(18 - 6c \neq 0\)
- Jibu
-
- 0
- haijafafanuliwa
Kurahisisha:
- \(\frac{0}{d - 4}\), wapi\(d \neq 4\)
- \(\frac{15 - 4q}{0}\), wapi\(15 - 4q \neq 0\)
- Jibu
-
- 0
- haijafafanuliwa
Kurahisisha:\(\frac{3}{4}\cdot\frac{4}{3}(6x + 12)\)
- Jibu
-
\[\begin{array} { l l } { } &{\frac{3}{4}\cdot\frac{4}{3}(6x + 12)} \\ { \text { There is nothing to do in the parentheses, } } &{}\\ { \text { so multiply the two fractions first—notice, } } &{1(6x + 12)} \\ { \text { they are reciprocals. } } &{} \\ \\{ \text { Simplify by recognizing the multiplicative } } &{} \\{\text{ identity.}} &{6x + 12} \end{array}\]
Kurahisisha:\(\frac{2}{5}\cdot\frac{5}{2}(20y + 50)\)
- Jibu
-
\(20y + 50\)
Kurahisisha:\(\frac{3}{8}\cdot\frac{8}{3}(12z + 16)\)
- Jibu
-
\(12z + 16\)
Kurahisisha Maneno Kutumia Mali ya Usambazaji
Tuseme kwamba marafiki watatu wanaenda kwenye sinema. Kila mmoja anahitaji $9.25 - hiyo ni dola 9 na robo-1 kulipa tiketi zao. Ni kiasi gani cha fedha wanahitaji wote pamoja?
Unaweza kufikiri juu ya dola tofauti na robo. Wanahitaji mara 3 $9 hivyo $27, na 3 mara 1 robo, hivyo senti 75. Kwa jumla, wanahitaji $27.75. Ikiwa unafikiri juu ya kufanya hesabu kwa njia hii, unatumia mali ya usambazaji.
\[\begin{array} { rr } {\text { If } a , b , c \text { are real numbers, then }} &{a ( b + c ) = a b + a c} \\ \\{ \text { Also,} } &{( b + c ) a = b a + c a} \\ {} &{a ( b - c ) = a b - a c } &{} \\{} &{( b - c ) a = b a - c a } \end{array}\]
Rudi kwa marafiki zetu kwenye sinema, tunaweza kupata jumla ya fedha wanayohitaji kama hii:
\[\begin{array} { c } { 3 ( 9.25 ) } \\ { 3 ( 9 + 0.25 ) } \\ { 3 ( 9 ) + 3 ( 0.25 ) } \\ { 27 + 0.75 } \\ \\ { 27.75 } \end{array}\]
Katika algebra, tunatumia mali ya kusambaza kuondoa mabano kama sisi kurahisisha maneno.
Kwa mfano, ikiwa tunaulizwa kurahisisha maneno\(3(x+4)\), utaratibu wa shughuli unasema kufanya kazi katika mabano kwanza. Lakini hatuwezi kuongeza x na 4, kwani si kama maneno. Kwa hiyo tunatumia mali ya usambazaji, kama inavyoonekana katika Zoezi\(\PageIndex{31}\).
Kurahisisha:\(3(x+4)\).
- Jibu
-
\[\begin{array} { l l } { } & { 3 ( x + 4 ) } \\ { \text { Distribute. } } & { 3 \cdot x + 3 \cdot 4 } \\ { \text { Multiply. } } & { 3 x + 12 } \end{array}\]
Kurahisisha:\(4(x+2)\).
- Jibu
-
\(4x + 8\)
Kurahisisha:\(6(x+7)\).
- Jibu
-
\(6x + 42\)
Wanafunzi wengine wanaona ni muhimu kuteka mishale kuwakumbusha jinsi ya kutumia mali ya kusambaza. Kisha hatua ya kwanza katika Zoezi\(\PageIndex{31}\) ingeonekana kama hii:
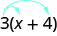
Kurahisisha:\(8(\frac{3}{8}x+\frac{1}{4})\).
- Jibu
-
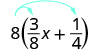
Kusambaza. 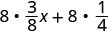
Kuzidisha. 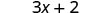
Kurahisisha:\(6(\frac{5}{6}y+\frac{1}{2})\).
- Jibu
-
\(5y + 3\)
Kurahisisha:\(12(\frac{1}{3}n+\frac{3}{4})\).
- Jibu
-
\(4n + 9\)
Kutumia mali ya usambazaji kama inavyoonekana katika Zoezi\(\PageIndex{37}\) itakuwa muhimu sana wakati sisi kutatua maombi fedha katika sura ya baadaye.
Kurahisisha:\(100(0.3+0.25q)\).
- Jibu
-
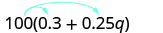
Kusambaza. 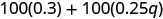
Kuzidisha. 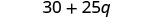
Kurahisisha:\(100(0.7+0.15p)\).
- Jibu
-
\(70 + 15p\)
Kurahisisha:\(100(0.04+0.35d)\).
- Jibu
-
\(4 + 35d\)
Tunaposambaza namba hasi, tunahitaji kuwa makini zaidi ili kupata ishara sahihi!
Kurahisisha:\(−2(4y+1)\).
- Jibu
-
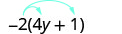
Kusambaza. 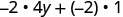
Kuzidisha. 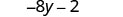
Kurahisisha:\(−3(6m+5)\).
- Jibu
-
\(−18m-15)\)
Kurahisisha:\(−6(8n+11)\).
- Jibu
-
\(−48n- 66)\)
Kurahisisha:\(−11(4-3a)\).
- Jibu
-
Kusambaza. 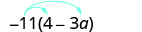
Kuzidisha. 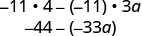
Kurahisisha. 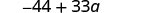
Kumbuka kwamba unaweza pia kuandika matokeo kama\(33a−44\). Unajua kwa nini?
Kurahisisha:\(−5(2-3a)\).
- Jibu
-
\(10+ 15a\)
Kurahisisha:\(−7(8-15y)\).
- Jibu
-
\(-56 + 105y\)
Zoezi\(\PageIndex{46}\) litaonyesha jinsi ya kutumia mali ya usambazaji ili kupata kinyume cha kujieleza.
Kurahisisha:\(−(y+5)\).
- Jibu
-
\[\begin{array} { ll } {} &{-(y + 5)} \\ \\{ \text {Multiplying by -1 results in the opposite.} } &{-1( y + 5 )} \\ \\ {\text{Distribute.}} &{-1\cdot y + (-1)\cdot 5}\\ \\{\text{Simplify.}} &{-y + (-5)} \\ \\ {} &{-y - 5} \end{array}\]
Kurahisisha:\(−(z-11)\).
- Jibu
-
\(-z + 11\)
Kurahisisha:\(−(x -4)\).
- Jibu
-
\(-x + 4\)
Kutakuwa na nyakati ambapo tutahitaji kutumia mali ya usambazaji kama sehemu ya utaratibu wa shughuli. Anza kwa kuangalia mabano. Ikiwa maneno ndani ya mabano hayawezi kuwa rahisi, hatua inayofuata itakuwa kuzidisha kwa kutumia mali ya kusambaza, ambayo huondoa mabano. Mifano miwili ijayo itaonyesha hili.
Kurahisisha:\(8−2(x + 3)\).
Hakikisha kufuata utaratibu wa shughuli. Kuzidisha huja kabla ya kuondoa, kwa hiyo tutasambaza 2 kwanza na kisha tuondoe.
- Jibu
-
\[\begin{array} { ll } {} &{8−2(x + 3)} \\ \\{ \text {Distribute.} } &{8−2\cdot x -2\cdot 3} \\ \\ {\text{Multiply.}} &{8 - 2x - 6}\\ \\{\text{Combine like terms.}} &{-2x + 2} \end{array}\]
Kurahisisha:\(9−3(x + 2)\).
- Jibu
-
\(3 - 3x\)
Kurahisisha:\(7x−5(x + 4)\).
- Jibu
-
\(2x - 20\)
Kurahisisha:\(4(x - 8)−(x + 3)\).
- Jibu
-
\[\begin{array} { ll } {} &{4(x - 8)−(x + 3)} \\ \\{ \text {Distribute.} } &{4x - 32 - x - 3} \\ \\{\text{Combine like terms.}} &{3x - 35} \end{array}\]
Kurahisisha:\(6(x - 9)−(x + 12)\).
- Jibu
-
\(5x - 66\)
Kurahisisha:\(8(x - 1)-(x + 5)\).
- Jibu
-
\(7x - 13\)
Mali yote ya namba halisi tumetumia katika sura hii ni muhtasari katika Jedwali\(\PageIndex{1}\).
| Comutative Mali | |
| ya kuongeza Ikiwa a, b ni namba halisi, kisha ya kuzidisha Kama a, b ni namba halisi, basi |
\(a+b=b+a\) \(a\cdot b=b\cdot a\) |
| Associative Mali | |
| ya kuongeza Ikiwa a, b, c ni namba halisi, kisha ya kuzidisha Ikiwa a, b, c ni namba halisi, basi |
\((a+b)+c=a+(b+c)\) \((a\cdot b)\cdot c=a\cdot (b\cdot c)\) |
| Mali ya Kusambaza | |
| Ikiwa, b, c ni namba halisi, basi | \(a(b+c)=ab+ac\) |
| Mali ya Identity | |
|
ya kuongeza Kwa idadi yoyote halisi a: ya kuzidisha Kwa idadi yoyote halisi a: |
\(a+0=a\) \(0+a=a\) \(1·a=a\) |
| Inverse Mali | |
| ya kuongeza Kwa yoyote ya kweli idadi a, \(−a\) ni livsmedelstillsats inverse ya kuzidisha Kwa idadi yoyote halisi\(a,a\neq 0\) \(\frac{1}{a}\) ni inverse multiplicative ya |
\(a+(−a)=0\) \(a\cdot\frac{1}{a}=1\) |
| Mali ya Zero | |
|
Kwa yoyote ya kweli idadi a, Kwa idadi yoyote halisi\(a,a\neq 0\) |
\(a\cdot 0=0\) \(0\cdot a=0\) \(\frac{0}{a} = 0\) |
Dhana muhimu
- Comutative Mali ya
- Aidha: Kama, b ni namba halisi, basi\(a+b=b+a\).
- Kuzidisha: Ikiwa a, b ni namba halisi, basi\(a\cdot b=b\cdot a\). Wakati wa kuongeza au kuzidisha, kubadilisha utaratibu hutoa matokeo sawa.
- Associative Mali ya
- Aidha: Ikiwa a, b, c ni namba halisi, basi\((a+b)+c=a+(b+c)\).
- Kuzidisha: Ikiwa a, b, c ni namba halisi, basi\((a\cdot b)\cdot c=a\cdot (b\cdot c)\).
Wakati wa kuongeza au kuzidisha, kubadilisha kikundi hutoa matokeo sawa.
- Distributive Mali: Kama, b, c ni idadi halisi, basi
- \(a(b+c)=ab+ac\)
- \((b+c)a=ba+ca\)
- \(a(b-c)=ab-ac\)
- \((b+c)a=ba-ca\)
- Mali ya Identity
- ya Aidha: Kwa yoyote halisi idadi a:\(a+0=a\)
0 ni livsmedelstillsats utambulisho - ya kuzidisha: Kwa idadi yoyote halisi a:\(a\cdot 1=a \quad 1·a=a\)
1 1 ni utambulisho multiplicative
- ya Aidha: Kwa yoyote halisi idadi a:\(a+0=a\)
- Inverse Mali
- ya Aidha: Kwa idadi yoyote halisi\(a, a+(−a)=0\). Nambari na kinyume chake huongeza sifuri. \(−a\)ni livsmedelstillsats inverse ya.
- ya Kuzidisha: Kwa idadi yoyote halisi\(a,(a\neq 0)a\cdot\frac{1}{a}=1\). Nambari na kurudi kwake huongezeka kwa moja. \(\frac{1}{a}\)ni inverse multiplicative ya.
- Mali ya Zero
- Kwa yoyote halisi idadi a,
\(a\cdot 0=0 \quad 0·a=0\) - bidhaa ya idadi yoyote halisi na 0 ni 0. - \(\frac{0}{a}=0\)kwa\(a\neq 0\) — Zero kugawanywa na idadi yoyote halisi isipokuwa sifuri ni sifuri.
- \(\frac{a}{0}\)ni undefined — Idara na sifuri ni undefined.
- Kwa yoyote halisi idadi a,


