1.4: Ongeza na Ondoa Integers
- Page ID
- 178114
- Tumia hasi na kupinga
- Kurahisisha: maneno yenye thamani kamili
- Ongeza integers
- Ondoa integers
Utangulizi wa kina zaidi wa mada yaliyofunikwa katika sehemu hii inaweza kupatikana katika sura ya Prealgebra, integers.
Tumia Hasi na Vikwazo
Kazi yetu hadi sasa imejumuisha namba za kuhesabu na namba nzima. Lakini ikiwa umewahi kupata joto chini ya sifuri au kwa ajali overdrawn akaunti yako ya kuangalia, tayari umejifunza na idadi hasi. Nambari mbaya ni idadi chini ya\(0\). Nambari hasi ni upande wa kushoto wa sifuri kwenye mstari wa namba. Angalia Kielelezo\(\PageIndex{1}\).
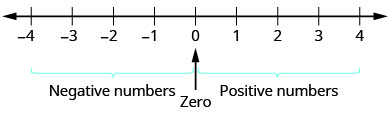
Mishale kwenye mwisho wa mstari wa nambari zinaonyesha kwamba namba zinaendelea kwenda milele. Hakuna idadi kubwa chanya, na hakuna ndogo idadi hasi.
Je, sifuri ni chanya au namba hasi? Hesabu kubwa kuliko sifuri ni chanya, na idadi ndogo kuliko sifuri ni hasi. Zero sio chanya wala hasi.
Fikiria jinsi namba zinavyoamriwa kwenye mstari wa nambari. Kwenda kutoka kushoto kwenda kulia, idadi huongezeka kwa thamani. Kwenda kutoka kulia kwenda kushoto, idadi hupungua kwa thamani. Angalia Kielelezo\(\PageIndex{2}\).
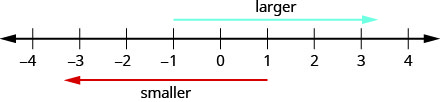
Kufanya shughuli za Hisabati za Manipulative “Nambari ya Mstari wa Sehemu ya 2” itakusaidia kuendeleza uelewa bora wa integers.
Kumbuka kwamba tunatumia notation:
\(a \lt b\)(soma “\(a\)ni chini ya\(b\)”) wakati\(a\) ni upande wa kushoto wa\(b\) kwenye mstari wa simu.
\(a \gt b\)(kusoma “\(a\)ni kubwa kuliko\(b\)”) wakati\(a\) ni na haki ya\(b\) juu ya mstari wa simu.
Sasa tunahitaji kupanua mstari namba ambayo ilionyesha idadi nzima ni pamoja na idadi hasi, pia. Nambari zilizowekwa na pointi katika Kielelezo\(\PageIndex{3}\). huitwa integers. Integers ni idadi\(...−3, −2, −1, 0, 1, 2, 3…\)

Agizo kila moja ya jozi zifuatazo za namba, kwa kutumia\(<\) au\(>\):
- \(14 \; \_\_\_\; 6\)
- \(-1\; \_\_\_ \;9\)
- \(-1\; \_\_\_ -4\)
- \(\;\; 2 \;\_\_\_ -20\)
Suluhisho:
Inaweza kuwa na manufaa kutaja mstari wa nambari iliyoonyeshwa.

Kielelezo\(\PageIndex{4}\)
\ (\ kuanza {align*} 1. \ quad & 14\;\ _\ _\ _\; 6\\ [4pt]
& 14 > 6 &&\ maandishi {\(14\)ni haki ya\(6\) kwenye mstari idadi.}\\ [8pt]
2. \ quad & -1\;\ _\ _\ _\; 9\\ [4pt]
& -1 <9 &&\ maandishi {\(-1\)ni upande wa kushoto wa\(9\) kwenye mstari namba.}\\ [8pt]
3. \ quad & -1\;\ _\ _\ _-4\\ [4pt]
& -1 > -4 &&\ maandishi {\(-1\)ni haki ya\(-4\) kwenye mstari idadi.}\\ [8pt]
4. \ quad & 2\;\ _\ _\ _-20\\ [4pt]
& 2 > -20 &&\ maandishi {\(2\)ni haki ya\(-20\) kwenye mstari idadi.} \
\ mwisho {align*}\)
Order kila moja ya jozi zifuatazo ya idadi, kwa kutumia\(<\) or \(>\):
- \(15 \; \_\_\_\; 7\)
- \(-2 \; \_\_\_\; 5\)
- \(-3 \; \_\_\_\; -7\)
- \(5 \; \_\_\_\; -17\)
- Answer
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Agizo kila moja ya jozi zifuatazo za namba, kwa kutumia\(<\) au\(>\):
- \(8 \; \_\_\_\; 13\)
- \(3 \; \_\_\_\; -4\)
- \(-5 \; \_\_\_\; -2\)
- \(9 \; \_\_\_\; -21\)
- Jibu
-
- \(<\)
- \(>\)
- \(<\)
- \(>\)
Huenda umeona kuwa, kwenye mstari wa nambari, namba hasi ni picha ya kioo ya namba nzuri, na sifuri katikati. Kwa sababu idadi\(2\) na\(−2\) ni umbali sawa kutoka sifuri, wao ni kuitwa kinyume s. Kinyume cha\(2\) ni\(−2\), na kinyume cha\(−2\) ni\(2\).
Kinyume cha namba ni namba ambayo ni umbali sawa kutoka sifuri kwenye mstari wa namba lakini upande wa pili wa sifuri.
Kielelezo\(\PageIndex{5}\) unaeleza ufafanuzi.

Wakati mwingine katika algebra ishara hiyo ina maana tofauti. Kama vile baadhi ya maneno katika Kiingereza, maana maalum inakuwa wazi kwa kuangalia jinsi inavyotumiwa. Umeona ishara “\(−\)” iliyotumiwa kwa njia tatu tofauti.
\ [kuanza {align*} &10 - 4\ quad\ maandishi {Kati ya namba mbili, inaonyesha uendeshaji wa}\ textit {kuondoa}.\\ &\ qquad\ qquad\ text {Tunasoma} 10 - 4\,\ maandishi {kama “} 10\,\ maandishi {minus}\, 4. \ Nakala {”}\\ [5pt]
&-8\ quad\ Nakala {Mbele ya idadi, inaonyesha}\ textit {hasi}\ Nakala {nambari.}\\ &\ qquad\\ maandishi {Tunasoma} -8\ maandishi {kama “hasi nane.”}\\ [5pt]
&-x\ quad\ Nakala {Mbele ya kutofautiana, inaonyesha}\ text tit {kinyume.}\\ &\ quad\ qquad\ maandishi {Tunasoma} -x\ maandishi {kama “kinyume cha} x\ maandishi {”}\\ [5pt]
&- (-2)\ quad\ maandishi {Hapa kuna ishara mbili “-”.} \\
&\ qquad\ qquad\ Nakala {Moja katika mabano inatuambia idadi ni hasi} 2. \\
&\ qquad\ qquad\ Nakala {Moja nje ya mabano inatuambia kuchukua}\ textit {kinyume}\ maandishi {ya} -2. \\
&\ qquad\ qquad\ text {Tunasoma} - (-2)\ maandishi {kama “kinyume cha mbili hasi.”} \ mwisho {align*}\]
\(−a\)ina maana kinyume cha idadi\(a\).
Nukuu\(−a\) inasomewa kama “kinyume cha\(a\).”
Kupata:
- kinyume cha\(7\)
- kinyume cha\(−10\)
- kinyume cha\(−(−6)\)
Suluhisho:
1. \( \quad −7\)ni umbali sawa na\(0\) kama\(7\), lakini upande wa pili wa\(0\). Kinyume cha\(7\) ni\(-7\).

2. \( \quad 10\)ni umbali sawa na\(0\) kama\(−10\), lakini upande wa pili wa\(0\). Kinyume cha\(-10\) ni\(10\).

3. \(\quad\)Kinyume cha\(-(-6)\) ni\(-6\).

Kupata:
- kinyume cha\(4\)
- the opposite of \(−3\)
- \(−(−1)\)
- Answer
-
- \(-4\)
- \(3\)
- \(1\)
Kupata:
- kinyume cha\(8\)
- kinyume cha\(−5\)
- \(−(−5)\)
- Jibu
-
- \(-8\)
- \(5\)
- \(5\)
Kazi yetu na kupinga inatupa njia ya kufafanua integers. Nambari nzima na kupinga kwao huitwa integers. Integers ni idadi\(…−3,−2,−1,0,1,2,3…\)
Nambari nzima na kupinga kwao huitwa integers.
Integers ni idadi
\[…−3,−2,−1,0,1,2,3… \nonumber \]
Wakati wa kutathmini kinyume cha kutofautiana, lazima tuwe makini sana. Bila kujua kama variable inawakilisha idadi chanya au hasi, hatujui kama -x-x ni chanya au hasi. Tunaweza kuona hii katika Mfano\(\PageIndex{1}\).
Tathmini
- \(-x\), lini\(x = 8\)
- \(-x\), lini\(x = -8\)
Suluhisho:
-

-x 
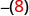
Andika kinyume cha 8. -8 -

-x 
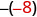
Andika kinyume cha -8. 8
Tathmini\(-n\), when
- \(n = 4\)
- \(n = -4\)
- Answer
-
- \(-4\)
- \(4\)
Tathmini\(-m\), wakati
- \(m = 11\)
- \(m = -11\)
- Jibu
-
- \(-11\)
- \(11\)
Kurahisisha: Maneno yenye Thamani kamili
Tuliona kwamba idadi kama vile\(2\) na\(−2\) ni kinyume kwa sababu wao ni umbali sawa kutoka\(0\) kwenye mstari namba. Wote wawili ni vitengo viwili kutoka\(0\). Umbali kati\(0\) na namba yoyote kwenye mstari wa namba inaitwa thamani kamili ya namba hiyo.
Thamani kamili ya namba ni umbali wake kutoka\(0\) kwenye mstari wa namba.
Thamani kamili ya namba\(n\) imeandikwa kama\(|n|\).
Kwa mfano,
- \(−5\)ni\(5\) vitengo mbali na\(0\), hivyo\(|−5|=5\).
- \(5\)ni\(5\) vitengo mbali na\(0\), hivyo\(|5|=5\).
Kielelezo\(\PageIndex{6}\) unaeleza wazo hili.
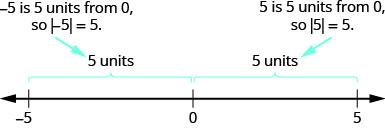
Thamani kamili ya namba haipatikani kamwe (kwa sababu umbali hauwezi kuwa hasi). Nambari pekee yenye thamani kamili sawa na sifuri ni namba sifuri yenyewe, kwa sababu umbali kutoka\(0\) hadi\(0\) kwenye mstari wa nambari ni vitengo vya sifuri.
\(|n| \geq 0\)kwa idadi zote
Maadili kamili ni daima zaidi kuliko au sawa na sifuri!
Wataalamu wa hisabati wanasema kwa usahihi zaidi, “maadili kamili ni daima yasiyo ya hasi.” Maana yasiyo ya hasi ina maana kubwa kuliko au sawa na sifuri.
Kurahisisha:
- \(|3|\)
- \(|-44|\)
- \(|0|\)
Suluhisho:
Thamani kamili ya namba ni umbali kati ya namba na sifuri. Umbali hauwezi kamwe hasi, hivyo thamani kamili haijawahi hasi.
- \( |3| = 3\)
- \(|-44| = 44\)
- \( |0| = 0\)
Kurahisisha:
- \(|4|\)
- \(|-28|\)
- \(|0|\)
- Answer
-
- \(4\)
- \(28\)
- \(0\)
Kurahisisha:
- \(|-13|\)
- \(|47|\)
- Jibu
-
- \(13\)
- \(47\)
Katika mfano unaofuata, tutaweza ili maneno na maadili kamili. Kumbuka, idadi nzuri daima ni kubwa kuliko idadi hasi!
Jaza\(<, >, \text{or} =\) kwa kila jozi zifuatazo za namba:
- \(|−5| \; {\underline{\hspace {2 em}}} \;−|−5|\)
- \(8 \;{\underline{\hspace {2 em}}} \;−|−8|\)
- \(-9 \;{\underline{\hspace {2 em}}} \;−|−9|\)
- \(-(-16) \;{\underline{\hspace {2 em}}}\; −|−16|\)
Suluhisho:
\(\begin{array} {llll} {\text{Simplification}} &{|-5|} & {\underline{\hspace {2 em}}} &{-|-5|} \\ {\text{Order.}} &{5} &{\underline{\hspace {2 em}}} &{-5} \\ {} &{5} &{>} &{-5} \\ {} &{|-5|} &{>} &{-|-5|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{8} & {\underline{\hspace {2 em}}} &{-|-8|} \\ {\text{Order.}} &{8} &{\underline{\hspace {2 em}}} &{-8} \\ {} &{8} &{>} &{-8} \\ \text{so }\\ {} & {|8|} &{>} &{-|-8|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-9} & {\underline{\hspace {2 em}}} &{-|-9|} \\ {\text{Order.}} &{-9} &{\underline{\hspace {2 em}}} &{-9} \\ {} &{-9} &{=} &{-9} \\ \text{so } \\ {} & {-9} &{=} &{-|-9|} \\ \end{array}\)
\(\begin{array} {llll} {\text{Simplification}} &{-(-16)} & {\underline{\hspace {2 em}}} &{-|16|} \\ {\text{Order.}} &{16} &{\underline{\hspace {2 em}}} &{-16} \\ {} &{16} &{>} &{-16} \\ \text{so } \\ {} & {-(-16)} &{>} &{-|-16|} \\ \end{array}\)
Jaza\(<, >, \text{or} =\) for each of the following pairs of numbers:
- \(|−9| \;{\underline{\hspace {2 em}}} \; −|−9|\)
- \(2 \;{\underline{\hspace {2 em}}} \; −|−2|\)
- \(-8 \;{\underline{\hspace {2 em}}} \; −|−8|\)
- \(-(-9) \;{\underline{\hspace {2 em}}} \; −|−9|\)
- Answer
-
- \(>\)
- \(>\)
- \(<\)
- \(>\)
Jaza\(<, >, \text{or} =\) kwa kila jozi zifuatazo za namba:
- \(7 \;{\underline{\hspace {2 em}}} \; −|−7|\)
- \(-(-10) \;{\underline{\hspace {2 em}}} \; −|−10|\)
- \(|-4| \;{\underline{\hspace {2 em}}} \; −|−4|\)
- \(-1 \;{\underline{\hspace {2 em}}} \; |−1|\)
- Jibu
-
- \(>\)
- \(>\)
- \(>\)
- \(<\)
Sasa tunaongeza baa za thamani kamili kwenye orodha yetu ya alama za makundi. Tunapotumia utaratibu wa shughuli, kwanza tunapunguza ndani ya baa za thamani kamili iwezekanavyo, basi tunachukua thamani kamili ya idadi inayosababisha.
\[\begin{array} {llll} {\text{Parentheses}} &{()} & {\text{Braces}} & {\{\}} \\ {\text{Brackets}} &{[\space]} &{\text{Absolute}} &{|\space|} \\ \end{array} \nonumber\]
Katika mfano unaofuata, sisi kurahisisha maneno ndani ya baa thamani kabisa kwanza, kama sisi kufanya na mabano.
Kurahisisha:\(24 - |19 - 3(6 - 2)|\)
Suluhisho:
\[\begin{array} {ll} {} &{24 - |19 - 3(6 - 2)|} \\ {\text{Work inside parentheses first: subtract } 2\space \text{from } 6} &{24 - |19 - 3(4)|} \\ {\text{Multiply }3(4)} &{24 - |19 - 12|} \\ {\text{Subtract inside the absolute value bars. }} &{24 - |7|} \\ {\text{Take the absolute value.}} &{24 - 7} \\ {\text{Subtract.}} &{17} \end{array}\nonumber\]
Kurahisisha:\(19 - |11 - 4(3 - 1)|\)
- Answer
-
\(16\)
Kurahisisha:\(9 - |8 - 4(7 - 5)|\)
- Jibu
-
\(9\)
Tathmini:
- \(|x|\)lini\(x = -35\)
- \(|y|\)lini\(y = -20\)
- \(-|u|\)lini\(u = 12\)
- \(-|p|\)lini\(p = -14\)
Suluhisho:
1. \(|x|\)lini\(x = -35\)
\(\begin{array} {ll} {} &{|x|} \\ {\text{Substitute } -35 \space \text{for }x} &{|-35|} \\ {\text{Take the absolute value.}} &{35} \end{array}\)
2. \(|y|\)lini\(y = -20\)
\(\begin{array} {ll} {} &{|-y|} \\ {\text{Substitute } -20 \space \text{for }y} &{|-(-20)|} \\ {\text{Simplify}} &{|20|} \\ {\text{Take the absolute value.}} &{20} \end{array}\)
3. \(-|u|\)lini\(u = 12\)
\(\begin{array} {ll} {} &{-|u|} \\ {\text{Substitute } 12 \space \text{for }u} &{|-12|} \\ {\text{Take the absolute value.}} &{-12} \end{array}\)
4. \(-|p|\)lini\(p = -14\)
\(\begin{array} {ll} {} &{-|p|} \\ {\text{Substitute } -14 \space \text{for }p} &{-|-14|} \\ {\text{Take the absolute value.}} &{-14} \end{array}\)
Tathmini:
- \(|x|\) when \(x = -17\)
- \(|y|\) when \(y = -39\)
- \(-|m|\) when \(m = 22\)
- \(-|p|\) when \(p = -11\)
- Answer
-
- \(17\)
- \(39\)
- \(-22\)
- \(-11\)
Tathmini:
- \(|y|\)lini\(y = -23\)
- \(|-y|\)lini\(y = -21\)
- \(-|n|\)lini\(n = 37\)
- \(-|q|\)lini\(q = -49\)
- Jibu
-
- \(23\)
- \(21\)
- \(-37\)
- \(-49\)
Ongeza integers
Wanafunzi wengi ni vizuri na kuongeza na kutoa ukweli kwa idadi chanya. Lakini kufanya kuongeza au kuondoa kwa namba zote mbili nzuri na hasi inaweza kuwa changamoto zaidi.
Kufanya shughuli za Hisabati za Manipulative “Kuongezea kwa Hesabu zilizosainiwa” zitakusaidia kuendeleza uelewa bora wa kuongeza integers.”
Tutatumia counters mbili za rangi ili kuongezea mfano na uondoaji wa hasi ili uweze kutazama taratibu badala ya kukariri sheria.
Tunaruhusu rangi moja (bluu) inawakilisha chanya. Rangi nyingine (nyekundu) itawakilisha hasi. Ikiwa tuna counter moja nzuri na counter moja hasi, thamani ya jozi ni sifuri. Wanaunda jozi ya neutral. Thamani ya jozi hii ya neutral ni sifuri.
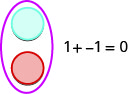
Tutatumia counters kuonyesha jinsi ya kuongeza ukweli nne kuongeza kwa kutumia namba\(5, −5\) na\(3,−3\).
\[\begin{array} {llll} {5 + 3} &{-5 + (-3)} &{-5 + 3} &{5 + (-3)} \end{array} \nonumber \]
Kuongeza\(5+3\), tunatambua kwamba\(5+3\) ina maana jumla ya\(5\) na\(3\).
| Tunaanza na\(5\) chanya. |  |
| Na kisha tunaongeza\(3\) chanya. |  |
| Sasa tuna\(8\) chanya. Jumla ya\(5\) na\(3\) ni\(8\). |  |
Sasa tutaongeza\(−5 + (−3)\). Tazama kufanana na mfano wa mwisho\(5 + 3 = 8\).
Ili kuongeza\(−5 + (−3)\), tunatambua hii ina maana ya jumla ya\(−5\) na\(−3\).
| Tunaanza na\(5\) hasi. |  |
| Na kisha tunaongeza\(3\) hasi. |  |
| Sasa tuna\(8\) hasi. Jumla ya\(-5\) na\(-3\) ni\(-8\). |  |
Kwa njia gani hizi mifano miwili ya kwanza ilikuwa sawa?
- Mfano wa kwanza unaongeza\(5\) chanya na\(3\) chanya - chanya zote mbili.
- Mfano wa pili unaongeza\(5\)\(3\) hasi na hasi - wote hasi.
Katika kila kesi tulipata\(8\) - ama\(8\) chanya au\(8\) hasi.
Wakati ishara zilikuwa sawa, counters walikuwa wote rangi sawa, na hivyo sisi aliongeza yao.

Ongeza:
- \(1 + 4\)
- \(-1 + (-4)\)
Suluhisho:
1. 
\(1\)\(4\)chanya pamoja na\(5\) chanya ni chanya.
2. 
\(1\)\(4\)hasi pamoja na\(5\) hasi ni hasi.
Ongeza:
- \(2 + 4\)
- \(-2 + (-4)\)
- Answer
-
- \(6\)
- \(-6\)
Ongeza:
- \(2 + 5\)
- \(-2 + (-5)\)
- Jibu
-
- \(7\)
- \(-7\)
Kwa nini kinatokea wakati ishara ni tofauti? Hebu tuongeze\(−5+3\). Tunatambua hii ina maana jumla ya\(−5\) na\(3\). Wakati counters walikuwa rangi sawa, tunawaweka mfululizo. Wakati counters ni rangi tofauti, tunawaweka chini ya kila mmoja.
| \(-5 + 3\)ina maana jumla ya\(-5\) na\(3\). | |
| Tunaanza na\(5\) hasi. |  |
| Na kisha tunaongeza\(3\) chanya. | 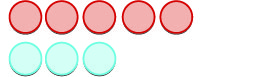 |
| Tunaondoa jozi yoyote ya neutral. | 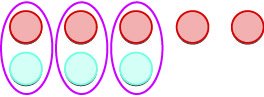 |
| Tuna\(2\) hasi kushoto. |  |
| Jumla ya\(-5\) na\(3\) ni\(-2\). | \(-5 + 3 = 2\) |
Angalia kwamba kulikuwa na hasi zaidi kuliko chanya, hivyo matokeo yalikuwa mabaya.
Hebu sasa tuongeze mchanganyiko wa mwisho,\(5+(−3)\).
| \(5 + (-3)\)ina maana jumla ya\(-5\) na\(-3\). | |
| Tunaanza na\(5\) chanya. |  |
| Na kisha tunaongeza\(3\) hasi. | 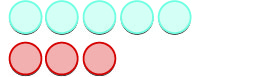 |
| Tunaondoa jozi yoyote ya neutral. | 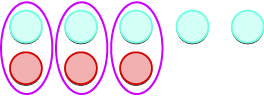 |
| Tuna\(2\) chanya kushoto. |  |
| Jumla ya\(5\) na\(-3\) ni\(2\). | \(5 + (-3) = 2\) |
Tunapotumia counters kwa mfano kuongeza ya integers chanya na hasi, ni rahisi kuona kama kuna counters chanya zaidi au zaidi hasi. Kwa hiyo tunajua kama jumla itakuwa chanya au hasi.
Ongeza:
- \(-1 + 5\)
- \(1 + (-5)\)
Suluhisho:
1. \(-1 + 5\)

Kuna chanya zaidi, hivyo jumla ni chanya.
Hivyo,\(-1 + 5 = 4\).
2. \(1 + (-5)\)

Kuna hasi zaidi, hivyo jumla ni hasi.
Hivyo,\(1 + (-5) = -4\)
Ongeza:
- \(-2 + 4\)
- \(2 + (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Ongeza:
- \(-2 + 5\)
- \(2 + (-5)\)
- Jibu
-
- \(3\)
- \(-3\)
Sasa kwa kuwa tumeongeza integers ndogo nzuri na hasi na mfano, tunaweza kutazama mfano katika akili zetu ili kurahisisha matatizo na namba yoyote.
Unapohitaji kuongeza namba kama vile\(37+(−53)\), hutaki kuhesabu hesabu za\(37\) bluu na counters\(53\) nyekundu. Kwa mfano katika akili yako, unaweza kutazama nini ungefanya ili kutatua tatizo?
Picha counters\(37\) bluu na counters\(53\) nyekundu lined up chini. Kwa kuwa kutakuwa na counters nyekundu (hasi) zaidi kuliko counters bluu (chanya), jumla itakuwa hasi. Je, kuna counters ngapi zaidi nyekundu ingekuwa? Kwa sababu\(53−37=16\), kuna counters\(16\) zaidi nyekundu.
Kwa hiyo, jumla ya\(37+(−53)\) ni\(−16\).
\[37+(−53)=−16\nonumber\]
Hebu jaribu mwingine. Tutaongeza\(−74+(−27)\). Tena, fikiria counters\(74\) nyekundu na counters nyekundu\(27\) zaidi, hivyo tunatarajia kuwa na counters\(101\) nyekundu. Hii ina maana jumla ni\(−101\).
\[−74+(−27)=−101\nonumber\]
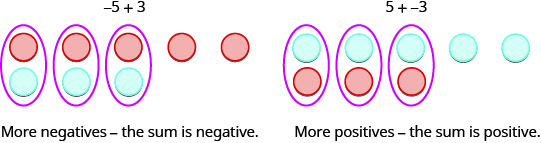
Hebu tuangalie tena matokeo ya kuongeza mchanganyiko tofauti wa\(5,−5\) na\(3, -3\).
\[\begin{array} {ll} {5 + 3=8} &{-5 + (-3)=-8} \\{\text{both positive, sum positive}} &{\text{both positive, sum positive}} \end{array}\nonumber\]
Wakati ishara ni sawa, counters itakuwa rangi sawa, hivyo kuongeza yao.
\[\begin{array} {ll} {5 + 3=-2} &{-5 + (-3)=2} \\{\text{different signs, more negatives, sum negative}} &{\text{different signs, more positives, sum positive}} \end{array}\nonumber\]
Wakati ishara ni tofauti, baadhi ya counters bila kufanya jozi neutral, hivyo Ondoa kuona ni wangapi kushoto.
Tazama mfano kama unapunguza maneno katika mifano ifuatayo.
Kurahisisha:
- \(19 + (-47)\)
- \(-14 + (-36)\)
Suluhisho:
1. Kwa kuwa ishara ni tofauti, tunaondoa\(19\) kutoka\(47\). Jibu litakuwa hasi kwa sababu kuna hasi zaidi kuliko chanya.
\(\text{Add.} \qquad 19 + (-47) = -28\)
2. Kwa kuwa ishara ni sawa, tunaongeza. Jibu litakuwa hasi kwa sababu kuna hasi zaidi kuliko chanya.
\(\text{Add.} \qquad-14 + (-36) = -50\)
Kurahisisha:
- \(-31 + (-19)\)
- \(15 + (-32)\)
- Answer
-
- \(-50\)
- \(-17\)
Kurahisisha:
- \(-42 + (-28)\)
- \(25 + (-61)\)
- Jibu
-
- \(-70\)
- \(-36\)
Mbinu zilizotumiwa hadi sasa zinaenea kwa matatizo magumu zaidi, kama yale tuliyoyaona kabla. Kumbuka kufuata utaratibu wa shughuli!
Kurahisisha:
\(-5 + 3(-2 + 7)\)
Suluhisho:
\[\begin{array} {ll} {} &{-5 + 3(-2 + 7)} \\ {\text{Simplify inside the parenthesis}} &{-5 + 3(5)} \\{\text{Multiply}} &{-5 + 15} \\{\text{add left to right}} &{10} \end{array}\nonumber\]
Kurahisisha:
\(-2 + 5(-4 + 7)\)
- Answer
-
\(13\)
Kurahisisha:
\(-4 + 2(-3 + 5)\)
- Jibu
-
\(0\)
Ondoa integers
Kufanya shughuli za Hisabati za Manipulative “Kuondoa Nambari zilizosainiwa” zitakusaidia kuendeleza uelewa bora wa kuondoa integers.
Tutaendelea kutumia counters ili kutengeneza uondoaji. Kumbuka, counters bluu kuwakilisha idadi chanya na counters nyekundu kuwakilisha idadi hasi.
Labda ulipokuwa mdogo, unasoma “\(5−3\)” kama “\(5\)uondoe\(3\).” Unapotumia counters, unaweza kufikiria kuondoa njia ile ile!
Sisi mfano nne kutoa ukweli kwa kutumia idadi\(5\) na\(3\).
\[\begin{array} {llll} {5 - 3} &{-5 - (-3))} &{-5 -3} &{5 - (-3)} \end{array}\nonumber\]
Ili kuondoa\(5−3\), tunarudia tena tatizo kama “\(5\)ondoa\(3\).”
| Tunaanza na\(5\) chanya. |  |
| Sisi 'kuchukua mbali'\(3\) chanya. |  |
| Tuna\(2\) chanya kushoto. | |
| Tofauti ya\(5\) na\(3\) ni\(2\). | \(2\) |
Sasa tutaondoa\(−5−(−3)\). Tazama kufanana na mfano wa mwisho\(5−3=2\).
Kuondoa\(−5−(−3)\), sisi restate hii kama “\(–5\)kuchukua mbali\(–3\)”
| Tunaanza na\(5\) hasi. |  |
|
Sisi 'kuondoa'\(3\) hasi. |
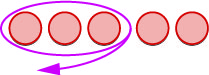 |
| Tuna\(2\) hasi kushoto. | |
| Tofauti ya\(-5\) na\(-3\) ni\(-2\). |
\(-2\) |
Angalia kwamba mifano hii miwili ni sawa sana: Mfano wa kwanza, tunaondoa chanya 3 kutoka kwa chanya cha 5 na kuishia na chanya 2.
Katika mfano wa pili, tunaondoa hasi 3 kutoka kwa negatives 5 na kuishia na hasi 2.
Kila mfano ulitumia counters ya rangi moja tu, na “kuchukua” mfano wa kuondoa ulikuwa rahisi kutumia.
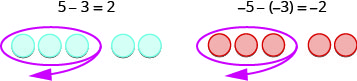
Ondoa:
- \(7 - 5\)
- \(-7 - (-5)\)
Suluhisho:
- \[\begin{array} {ll} {7 - 5} \\ {2}&{\text{Take }5\space \text{positives from }7 \space \text{positives and get }2\space \text{positives}} & \end{array}\nonumber\]
- \[\begin{array} {ll} {-7 - (-5)} \\ {-2} &{\text{Take }5\space \text{negatives from }7 \space \text{negatives and get }2\space \text{negatives}} \end{array}\nonumber\]
Ondoa:
- \(6 - 4\)
- \(-6 - (-4)\)
- Answer
-
- \(2\)
- \(-2\)
Ondoa:
- \(7 - 4\)
- \(-7 - (-4)\)
- Jibu
-
- \(3\)
- \(-3\)
Ni nini kinachotokea wakati tunapaswa kuondoa namba moja nzuri na moja hasi? Tutahitaji kutumia counters nyeupe na nyekundu pamoja na jozi zingine za neutral. Kuongeza jozi ya neutral haina mabadiliko ya thamani. Ni kama kubadilisha robo kwa nickels-thamani ni sawa, lakini inaonekana tofauti.
- Ili kuondoa\(−5−3\), tunarudia tena kama\(−5\) kuchukua\(3\).
Tunaanza na\(5\) hasi. Tunahitaji kuchukua\(3\) chanya, lakini hatuna chanya cha kuchukua.
Kumbuka, jozi ya neutral ina thamani sifuri. Kama sisi\(0\) kuongeza thamani\(5\) yake bado\(5\). Sisi kuongeza jozi neutral\(5\) kwa hasi mpaka sisi kupata\(3\) chanya kuchukua mbali.
| \(-5 -3\)ina maana ya\(-5\) kuchukua\(3\) | |
| Tunaanza na\(5\) hasi. |  |
| Sasa tunaongeza wasio na nia zinazohitajika kupata\(3\) chanya. |  |
| Sisi kuondoa\(3\) chanya. | 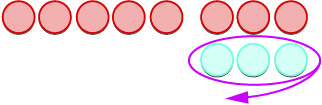 |
| Sisi ni wa kushoto na\(8\) hasi. |  |
| Tofauti ya\(-5\) na\(3\) ni\(-8\). | \(-5 - 3 = -8\) |
Na sasa, kesi ya nne,\(5−(−3)\). Tunaanza na\(5\) chanya. Tunahitaji kuondoa\(3\) hasi, lakini hakuna hasi za kuchukua. Hivyo sisi kuongeza jozi neutral mpaka tuna\(3\) negatives kuchukua mbali.
| \(5 -(-3)\)ina maana ya\(5\) kuchukua\(-3\) | |
| Tunaanza na\(5\) chanya. |  |
| Sasa tunaongeza jozi zinazohitajika za neutral. |  |
| Sisi kuondoa\(3\) hasi. | 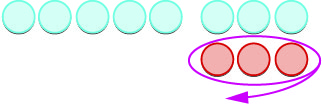 |
| Sisi ni wa kushoto na\(8\) chanya. |  |
| Tofauti ya\(5\) na\(-3\) ni\(8\). | \(5 - (-3) = 8\) |
Ondoa:
- \(-3 -1\)
- \(3 - (-1)\)
Suluhisho:
1.
|
Chukua chanya 1 kutoka kwa jozi moja ya neutral iliyoongezwa. |
  |
\(\begin{array} {l} {-3 -1} \\ {-4} \end{array}\) |
|
Chukua hasi 1 kutoka kwa jozi moja ya neutral iliyoongezwa. |
  |
\(\begin{array} {l} {3 - (-1)} \\ {4} \end{array}\) |
Ondoa:
- \(-6 -4\)
- \(6 - (-4)\)
- Answer
-
- \(-10\)
- \(10\)
Ondoa:
- \(-7-4\)
- \(7 - (-4)\)
- Jibu
-
- \(-11\)
- \(11\)
Je! Umeona kuwa uondoaji wa namba zilizosainiwa unaweza kufanywa kwa kuongeza kinyume? Katika Zoezi\(\PageIndex{33}\),\(−3−1\) ni sawa\(−3+(−1)\) na\(3−(−1)\) ni sawa na\(3+1\). Mara nyingi utaona wazo hili, mali ya kuondoa, iliyoandikwa kama ifuatavyo:
\[a−b=a+(−b) \nonumber\]
Kuondoa namba ni sawa na kuongeza kinyume chake.
Angalia mifano hii miwili.
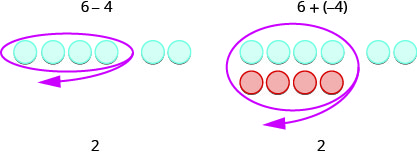
Bila shaka, wakati una tatizo la kuondoa ambalo lina idadi nzuri tu\(6−4\), kama, unafanya tu kuondoa. Tayari ulijua jinsi ya kuondoa\(6−4\) muda mrefu uliopita. Lakini kujua kwamba\(6−4\) anatoa jibu sawa na\(6+(−4)\) husaidia wakati wewe ni kuondoa idadi hasi. Hakikisha kwamba unaelewa jinsi\(6−4\) na\(6+(−4)\) kutoa matokeo sawa!
Kurahisisha:
- \(13 - 8 \space \text{and } 13 + (-8)\)
- \(-17 - 9 \space \text{and } -17 + (-9)\)
Suluhisho:
- \(\begin{array} {llll} {\text{Subtract.}} &{13 - 8} &{\text{and}} &{13 + (-8)} \\ {} &{5} &{} &{5} \end{array}\)
- \(\begin{array} {llll} {\text{Subtract.}} &{-17 - 9} &{\text{and}} &{-17 + (-9)} \\ {} &{-26} &{} &{-26} \end{array}\)
Kurahisisha:
- \(21 - 13 \space \text{and } 21 + (-13)\)
- \(-11 - 7 \space \text{and } -11 + (-7)\)
- Answer
-
- \(8\)
- \(-18\)
Kurahisisha:
- \(15 - 7 \space \text{and } 15 + (-7)\)
- \(-14 - 8 \space \text{and } -14 + (-8)\)
- Jibu
-
- \(8\)
- \(-22\)
Angalia nini kinatokea wakati sisi Ondoa hasi.

Kuondoa idadi hasi ni kama kuongeza chanya!
Wewe mara nyingi kuona hii imeandikwa kama\(a−(−b)=a+b\).
Je, kwamba kazi kwa idadi nyingine, pia? Hebu tufanye mfano unaofuata na uone.
Kurahisisha:
- \(9 - (-15) \space \text{and } 9 + 15\)
- \(-7 - (-4) \space \text{and } -7 + 4\)
Suluhisho:
- \(\begin{array} {lll} {} &{9 - (-15)} &{9 + 15} \\ {\text{Subtract}} &{24} &{24} \end{array}\)
- \(\begin{array} {lll} {} &{-7 - (-4)} &{-7 + 4} \\ {\text{Subtract}} &{-3} &{-3} \end{array}\)
Kurahisisha:
- \(6 - (-13) \space \text{and } 6 + 13\)
- \(-5 - (-1) \space \text{and } -5 + 1\)
- Answer
-
- \(19\)
- \(-4\)
Kurahisisha:
- \(4 - (-19) \space \text{and } 4 + 19\)
- \(-4 - (-7) \space \text{and } -4 + 7\)
- Jibu
-
- \(23\)
- \(3\)
Hebu tuangalie tena matokeo ya kuondoa mchanganyiko tofauti wa\(5,−5\) na\(3,−3\).
\[\begin{array} {l} {5 - 3} &{-5 - (-3)} \\ {2} &{-2} \\ {5\space\text{positives take away }3\space\text{positives}} &{5\space\text{negatives take away }3\space\text{negatives}} \\ {2\space\text{positives}} &{2\space\text{negatives}} \end{array}\nonumber\]
Wakati kutakuwa na counters ya kutosha ya rangi ya kuchukua, Ondoa.
\[\begin{array} {l} {-5 - 3} &{5 - (-3)} \\ {-8} &{8} \\ {5\space\text{negatives, want to take away }3\space\text{positives}} &{5\space\text{positives, want to take away }3\space\text{negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}} \end{array}\nonumber\]
Wakati hakutakuwa na counters ya kutosha ya rangi ya kuchukua, ongeza.
Nini kinatokea wakati kuna integers zaidi ya tatu? Tunatumia tu utaratibu wa shughuli kama kawaida.
Kurahisisha:
\(7 - (-4 -3) - 9\)
Suluhisho:
\[ \begin{array} {ll} {} &{7 - (-4 - 3) - 9} \\ {\text{Simplify inside the parenthesis first.}} &{7 - (-7) - 9} \\ {\text{Subtract left to right.}} &{14 - 9} \\ {\text{Subtract}} &{5} \end{array}\nonumber\]
Kurahisisha:
\(8−(−3−1)−9\)
- Answer
-
\(3\)
Kurahisisha:
\(12−(−9−6)−14\)
- Jibu
-
\(12\)
Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na kuongeza na kuondoa integers. Utahitaji kuwezesha Java kwenye kivinjari chako cha wavuti ili utumie programu.
Dhana muhimu
- Kuongezea kwa Integers Chanya na Hasi
\[\begin{array} {ll} {5 + 3} &{-5+(-3)} \\ {8} &{-8} \\ {\text{both positive,}} &{\text{both negative,}} \\ {\text{sum positive}} &{\text{sum negative}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 + 3} &{5+(-3)} \\ {-2} &{2} \\ {\text{different signs,}} &{\text{different signs,}} \\ {\text{more negatives}} &{\text{more positives}} \\ {\text{sum negative}} &{\text{sum positive}} \end{array}\nonumber\]
- Mali ya Thamani kamili:
\(|n| \geq 0\)kwa idadi yote. Maadili kamili ni daima zaidi kuliko au sawa na sifuri!
- Uondoaji wa integers
\[\begin{array} {ll} {5 - 3} &{-5-(-3)} \\ {2} &{-2} \\ {5\space\text{positives}} &{5\space\text{negatives}} \\ {\text{take away 3 positives}} &{\text{take away 3 negatives}} \\ {\text{2 positives}} &{\text{2 negatives}} \end{array}\nonumber\]
\[\begin{array} {ll} {-5 - 3} &{5-(-3)} \\ {-8} &{8} \\ {\text{5 negatives, want to}} &{\text{5 positives, want to}} \\ {\text{subtract 3 positives}} &{\text{subtract 3 negatives}} \\ {\text{need neutral pairs}} &{\text{need neutral pairs}}\end{array}\nonumber\]
- Ondoa Mali: Kutoa idadi ni sawa na kuongeza kinyume chake.
faharasa
- thamani kamili
- Thamani kamili ya namba ni umbali wake kutoka 0 kwenye mstari wa namba. Thamani kamili ya nambari nn imeandikwa kama |n|.
- namba kamili
- Nambari nzima na kupinga kwao huitwa integers:\(...−3, −2, −1, 0, 1, 2, 3...\)
- kinyume
- Kinyume cha namba ni namba ambayo ni umbali sawa kutoka sifuri kwenye mstari wa namba lakini upande wa pili wa sifuri:\(a\) -inamaanisha kinyume cha namba. Nukuu -\(a\) inasomewa “kinyume cha\(a\).”


