Skip to main content
Global

1.2: Utangulizi wa Hesabu Nzima

  1. Last updated
  2. Save as PDF
  • Page ID
    177925

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Mwishoni mwa sehemu hii, utaweza:
    • Tumia thamani ya mahali na namba nzima
    • Kutambua wingi na kutumia vipimo vya mgawanyiko
    • Kupata factorizations mkuu na mafungu angalau ya kawaida

    Tunapoanza utafiti wetu wa algebra ya msingi, tunahitaji kurejesha baadhi ya ujuzi wetu na msamiati. Sura hii italenga idadi nzima, integers, FRACTIONS, decimals, na idadi halisi. Tutaanza pia matumizi yetu ya notation algebraic na msamiati.

    Tumia Thamani ya Mahali na Hesabu Nzima

    Nambari za msingi zinazotumiwa katika algebra ni namba tunazozitumia kuhesabu vitu katika ulimwengu wetu:\(1, 2, 3, 4\), na kadhalika. Hizi huitwa namba ya kuhesabu s. Nambari za kuhesabu pia huitwa namba asilia. Kama sisi kuongeza sifuri kwa idadi kuhesabu, sisi kupata seti ya idadi nzima s.

    • Hesabu Hesabu:\(1, 2, 3, …\)
    • Hesabu nzima:\(0, 1, 2, 3, …\)

    Notation “\(…\)” inaitwa ellipsis na ina maana “na kadhalika,” au kwamba muundo unaendelea milele.

    Tunaweza kutazama namba za kuhesabu na namba nzima kwenye mstari wa namba (angalia Mchoro\(\PageIndex{1}\)).

    Mstari wa namba ya usawa na mishale kwenye kila mwisho na maadili ya sifuri hadi sita huendesha chini ya mchoro. Mstari wa pili wa usawa na mshale unaoelekea kushoto uongo juu ya kwanza na kupanua kutoka sifuri hadi tatu. Mstari huu umeitwa “ndogo”. Mstari wa tatu wa usawa na mshale unaoelekea kulia uongo juu ya mbili za kwanza, lakini huendesha kutoka tatu hadi sita na inaitwa “kubwa”.
    Kielelezo\(\PageIndex{1}\): Idadi kwenye mstari wa nambari hupata kubwa kama wanaenda kutoka kushoto kwenda kulia, na ndogo kama wanaenda kutoka kulia kwenda kushoto. Wakati mstari huu namba inaonyesha tu namba nzima\(0\) kwa njia ya\(6\), namba kuendelea bila mwisho.

    Kufanya shughuli za Hisabati za Manipulative “Idadi Line-Sehemu ya 1” itakusaidia kuendeleza uelewa bora wa namba za kuhesabu na namba nzima.

    Mfumo wetu wa nambari huitwa mfumo wa thamani ya mahali, kwa sababu thamani ya tarakimu inategemea nafasi yake kwa idadi. Kielelezo\(\PageIndex{2}\) kinaonyesha maadili ya mahali. Maadili ya mahali yanatenganishwa katika makundi ya matatu, ambayo huitwa vipindi. Kipindi ni ndio, maelfu, mamilioni, mabilioni, trilioni, na kadhalika. Katika namba iliyoandikwa, koma hutenganisha vipindi.

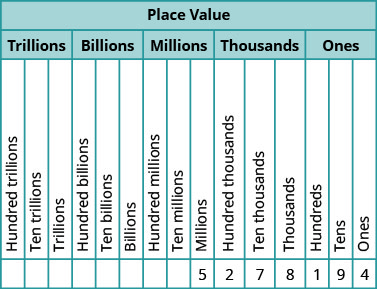
    Takwimu hii ni meza inayoonyesha namba 5,278,194 ndani ya mfumo wa thamani ya mahali. Jedwali linaonyeshwa kwa mstari wa kichwa, kinachoitwa “Thamani ya Mahali”, imegawanywa katika mstari wa pili wa kichwa kinachoitwa “Trillions”, “Mabilioni”, “Mamilioni”, “Maelfu” na “Wale”. Chini ya kichwa “Trillions” ni nguzo tatu zilizoandikwa, zilizoandikwa kutoka chini hadi juu, ambazo zinasoma “trilioni mia”, “Trilioni kumi” na “Trillions”. Chini ya kichwa “Mabilioni” ni tatu lebo nguzo, imeandikwa kutoka chini hadi juu, kwamba kusoma “Mabilioni mia”, “Mabilioni kumi” na “Mabilioni”. Chini ya kichwa “Mamilioni” ni nguzo tatu zilizoandikwa, zilizoandikwa kutoka chini hadi juu, ambazo zinasoma “mamilioni mia”, “Mamilioni kumi” na “Mamilioni”. Chini ya kichwa “Maelfu” ni nguzo tatu zilizoandikwa, zilizoandikwa kutoka chini hadi juu, ambazo zinasoma “maelfu mia”, “Maelfu kumi” na “Maelfu”. Chini ya kichwa “Wale” ni nguzo tatu zilizoandikwa, zilizoandikwa kutoka chini hadi juu, ambazo zinasoma “Mamia”, “Makumi” na “Wale”. Kutoka kushoto kwenda kulia, chini ya nguzo kinachoitwa “Mamilioni”, “Mia maelfu”, “Maelfu kumi”, “Maelfu”, “Mamia”, “Makumi”, na “Wale”, ni maadili yafuatayo: 5, 2, 7, 8, 1, 9, 4. Hii ina maana kuna mamilioni 5, maelfu mia 2, 7 maelfu kumi, maelfu 8, mamia 1, makumi 9, na 4 katika idadi milioni tano mia mbili sabini na tisa elfu moja mia moja tisini na nne.
    Kielelezo\(\PageIndex{2}\): Nambari\(5278194\) inavyoonekana kwenye chati. Nambari\(5\) iko katika mahali mamilioni. Nambari\(2\) iko mahali pa mia maelfu. Nambari\(7\) iko katika mahali pa maelfu kumi. Nambari\(8\) iko mahali pa maelfu. Nambari\(1\) iko katika sehemu ya mamia. Nambari\(9\) iko mahali pa makumi. Nambari\(4\) iko mahali pekee.
    Zoezi\(\PageIndex{1}\)

    Kwa idadi\(63407218\), pata thamani ya mahali ya kila tarakimu:

    1. \(7\)
    2. \(0\)
    3. \(1\)
    4. \(6\)
    5. \(3\)
    Jibu

    Weka nambari katika chati ya thamani ya mahali:

    Takwimu hii ni meza inayoonyesha namba 63,407,218 ndani ya mfumo wa thamani ya mahali. Jedwali linaonyeshwa kwa mstari wa kichwa, kinachoitwa “Thamani ya Mahali”, imegawanywa katika mstari wa pili wa kichwa kinachoitwa “Trillions”, “Mabilioni”, “Mamilioni”, “Maelfu” na “Wale”. Chini ya kichwa “Trillions” ni nguzo tatu zilizoandikwa, zilizoandikwa kutoka chini hadi juu, ambazo zinasoma “trilioni mia”, “Trilioni kumi” na “Trillions”. Chini ya kichwa “Mabilioni” ni tatu lebo nguzo, imeandikwa kutoka chini hadi juu, kwamba kusoma “Mabilioni mia”, “Mabilioni kumi” na “Mabilioni”. Chini ya kichwa “Mamilioni” ni nguzo tatu zilizoandikwa, zilizoandikwa kutoka chini hadi juu, ambazo zinasoma “mamilioni mia”, “Mamilioni kumi” na “Mamilioni”. Chini ya kichwa “Maelfu” ni nguzo tatu zilizoandikwa, zilizoandikwa kutoka chini hadi juu, ambazo zinasoma “maelfu mia”, “Maelfu kumi” na “Maelfu”. Chini ya kichwa “Wale” ni nguzo tatu zilizoandikwa, zilizoandikwa kutoka chini hadi juu, ambazo zinasoma “Mamia”, “Makumi” na “Wale”. Kutoka kushoto kwenda kulia, chini ya nguzo kinachoitwa “Mamilioni kumi”, “Mamilioni”, “Mia maelfu”, “Maelfu kumi”, “Maelfu”, “Mamia”, “Makumi”, na “Wale”, ni maadili yafuatayo: 6, 3, 4, 0, 7, 2, 1, 8. Hii ina maana kuna 6 mamilioni kumi, mamilioni 3, maelfu mia 4, 0 maelfu kumi, 7 maelfu, mamia 2, 1 kumi, na 8 katika idadi sitini na tatu milioni, mia nne saba elfu, mia mbili kumi na nane.
    1. The\(7\) ni katika maelfu mahali.
    2. The\(0\) ni katika maelfu kumi mahali.
    3. Ya\(1\) ni katika makumi mahali.
    4. Ya\(6\) ni katika mahali kumi mamilioni.
    5. The\(3\) ni katika mamilioni mahali.
    Zoezi\(\PageIndex{2}\)

    Kwa idadi\(27493615\), tafuta thamani ya mahali ya kila tarakimu:

    1. 2
    2. 1
    3. 4
    4. 7
    5. 5
    Jibu
    1. mamilioni kumi
    2. makumi
    3. maelfu mia
    4. mamilioni
    5. mmojammoja
    Zoezi\(\PageIndex{3}\)

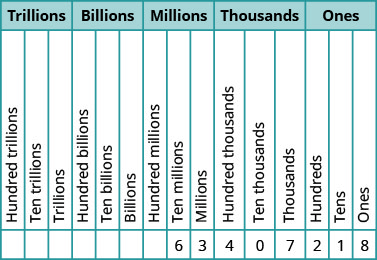
    Kwa idadi\(519711641328\), tafuta thamani ya mahali ya kila tarakimu:

    1. 9
    2. 4
    3. 2
    4. 6
    5. 7
    Jibu
    1. mabilioni
    2. maelfu kumi
    3. makumi
    4. maelfu mia
    5. mamilioni mia

    Unapoandika hundi, unaandika nambari kwa maneno pamoja na tarakimu. Kuandika nambari kwa maneno, weka nambari katika kila kipindi, ikifuatiwa na jina la kipindi, bila s mwishoni. Anza upande wa kushoto, ambapo vipindi vina thamani kubwa zaidi. Kipindi hicho hakijaitwa jina. Vipande hutenganisha vipindi, hivyo popote popote kuna comma katika nambari, weka comma kati ya maneno (angalia Mchoro\(\PageIndex{3}\)). Idadi hiyo\(74218369\) imeandikwa kuwa milioni sabini na nne, mia mbili kumi na nane elfu, mia tatu sitini na tisa.

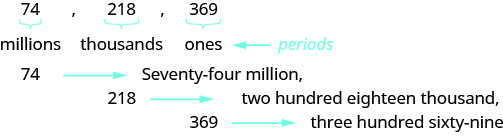
    Katika takwimu hii, namba 74, 218 na 369 zimeorodheshwa mfululizo, zikitenganishwa na commas. Kila namba ina mabano ya curly chini yake na neno “mamilioni” lililoandikwa chini ya namba 74, “maelfu” yaliyoandikwa chini ya namba 218, na “wale” iliyoandikwa chini ya namba 369. Mshale unaoelekea kushoto unaonyesha maneno haya matatu, akiwaandikisha “vipindi”. Mstari mmoja chini ni namba “74”, mshale unaoelekea kulia na maneno “milioni sabini na nne” ikifuatiwa na comma. Mstari uliofuata chini ni namba “218", mshale unaoelekea kulia na maneno “mia mbili kumi na nane elfu” ikifuatiwa na comma. Kwenye mstari wa chini ni namba “369", mshale unaoelekea kulia na maneno “mia tatu sitini na tisa”.
    Kielelezo\(\PageIndex{3}\)
    JINA NAMBARI NZIMA KWA MANENO.
    1. Anza upande wa kushoto na jina namba katika kila kipindi, ikifuatiwa na jina la kipindi.
    2. Weka koma katika nambari ili kutenganisha vipindi.
    3. Je, si jina la kipindi hicho.
    Zoezi\(\PageIndex{4}\)

    Jina namba\(8165432098710\) kwa kutumia maneno.

    Jibu

    Jina namba katika kila kipindi, ikifuatiwa na jina la kipindi.

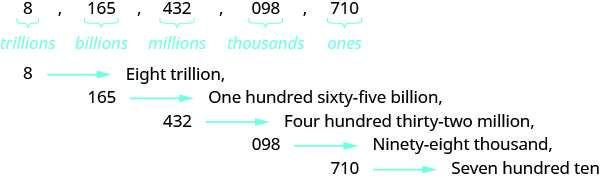
    Katika takwimu hii, namba 8, 165, 432, 098 na 710 zimeorodheshwa mfululizo, zikitenganishwa na commas. Kila namba ina mabano ya usawa chini na neno “trillions” lililoandikwa chini ya namba 8, “mabilioni” yaliyoandikwa chini ya namba 165, “mamilioni” iliyoandikwa chini ya namba 432, “maelfu” yaliyoandikwa chini ya namba 098, na “zile” zilizoandikwa chini ya namba 710. Mstari mmoja chini ni namba 8, mshale unaoelekea kulia na maneno “trilioni nane” ikifuatiwa na comma. Katika mstari unaofuata chini ni namba 165, mshale unaoelekea kulia na maneno “Bilioni mia moja sitini na tano” ikifuatiwa na comma. Katika mstari unaofuata chini ni namba 432, mshale unaoelekea kulia na maneno “Mia nne thelathini na mbili milioni” ikifuatiwa na comma. Katika mstari unaofuata chini ni namba “098”, mshale unaoelekea kulia na maneno “Tisini na nane elfu” ikifuatiwa na comma. Kwenye mstari wa chini ni namba 710, mshale unaoelekea kulia na maneno “Mia saba kumi”.

    Weka commas katika kutenganisha vipindi.

    Kwa hiyo, jina lake\(8165432098710\) ni trilioni nane, bilioni mia moja sitini na tano, milioni mia nne thelathini na mbili, tisini na nane elfu, mia saba kumi.

    Zoezi\(\PageIndex{5}\)

    Jina namba 9,258,137,904,0619,258,137,904,061 kwa kutumia maneno.

    Jibu

    trilioni tisa, mia mbili hamsini na nane bilioni, milioni mia moja thelathini na saba, mia tisa nne elfu, sitini na moja

    Zoezi\(\PageIndex{6}\)

    Jina namba 17,864,325,619,00417,864,325,619,004 kwa kutumia maneno.

    Jibu

    trilioni kumi na saba, mia nane sitini na nne bilioni, milioni mia tatu ishirini na tano, mia sita kumi na tisa elfu nne

    Sasa tunakwenda kurekebisha mchakato kwa kuandika tarakimu kutoka kwa jina la nambari. Kuandika nambari kwa tarakimu, sisi kwanza tunatafuta maneno ya kidokezo ambayo yanaonyesha vipindi. Inasaidia kuteka safu tatu kwa vipindi vinavyohitajika na kisha kujaza vifungo na namba, kutenganisha vipindi na commas.

    ANDIKA NAMBA NZIMA KWA KUTUMIA TARAKIMU.
    1. Tambua maneno yanayoonyesha vipindi. (Kumbuka, kipindi hicho hakijaitwa kamwe.)
    2. Chora vifungo vitatu ili kuonyesha idadi ya maeneo inahitajika kila kipindi. Toa vipindi kwa commas.
    3. Jina namba katika kila kipindi na uweke tarakimu katika nafasi sahihi ya thamani ya mahali.
    Zoezi\(\PageIndex{7}\)

    Andika bilioni tisa, milioni mia mbili arobaini na sita, sabini na tatu elfu, mia moja themanini na tisa kama namba nzima kwa kutumia tarakimu.

    Jibu

    Tambua maneno yanayoonyesha vipindi.
    Isipokuwa kwa kipindi cha kwanza, vipindi vingine vyote lazima iwe na sehemu tatu. Chora vifungo vitatu ili kuonyesha idadi ya maeneo inahitajika kila kipindi. Toa vipindi kwa commas.
    Kisha kuandika tarakimu katika kila kipindi.

    Picha ina mistari miwili ya maandishi. Mstari wa juu unasoma “bilioni tisa”, ikifuatiwa na comma, na “milioni mia mbili arobaini na sita”, pia ikifuatiwa na comma. Maneno “bilioni” na “milioni” yamesisitizwa na kila maneno ina bracket curly chini. Mstari wa chini unasoma “sabini na tatu elfu”, ikifuatiwa na comma, na “mia moja themanini na tisa”. Neno “elfu” linasisitizwa na kila maneno ina bracket curly chini.

    Idadi ni 9,246,073,189.
    Zoezi\(\PageIndex{8}\)

    Andika namba bilioni mbili, milioni mia nne sitini na sita, mia saba kumi na nne elfu, hamsini na moja kwa namba nzima kwa kutumia tarakimu.

    Jibu

    2,466,714,051

    Zoezi\(\PageIndex{9}\)

    Andika namba bilioni kumi na moja, milioni mia tisa ishirini na moja, mia nane thelathini elfu, mia moja sita kwa namba nzima kwa kutumia tarakimu.

    Jibu

    11,921,830,106

    Mwaka 2013, Ofisi ya Sensa ya Marekani ilikadiria idadi ya wakazi wa jimbo la New York kuwa 19,651,127. Tunaweza kusema idadi ya wakazi wa New York ilikuwa takriban milioni 20. Mara nyingi, huhitaji thamani halisi; nambari ya takriban ni nzuri ya kutosha.

    Mchakato wa kukadiria idadi inaitwa mviringo. Hesabu zimezunguka kwa thamani maalum ya mahali, kulingana na usahihi gani unahitajika. Kusema kuwa idadi ya watu wa New York ni takriban 20 milioni ina maana kwamba sisi mviringo kwa mamilioni mahali.

    Zoezi\(\PageIndex{10}\) How to Round Whole Numbers

    Pande zote 23,658 kwa mia karibu.

    Jibu

    Takwimu hii ni meza ambayo ina nguzo tatu na safu nne. Safu ya kwanza ni safu ya kichwa, na ina majina na namba za kila hatua. Safu ya pili ina maelekezo zaidi yaliyoandikwa. Safu ya tatu ina namba zinazohusiana na hatua zilizoandikwa na maelekezo. Katika mstari wa juu, kiini cha kwanza kinasema: “Hatua ya 1. Pata thamani ya mahali uliyopewa na mshale. Nambari zote upande wa kushoto hazibadilika.” Katika kiini cha pili, maelekezo yanasema: “Pata mahali mamia katika 23,658.” Katika kiini cha tatu, kuna namba 23,658 yenye mshale unaoelezea tarakimu 6, akiiandika “mahali mamia.”Mstari mmoja chini, maagizo katika kiini cha kwanza husema: “Hatua ya 2. Sisitiza tarakimu kwa haki ya thamani ya mahali uliyopewa.” Katika kiini cha pili, maagizo yanasema: “Weka 5, ambayo ni haki ya mahali pa mamia.” Katika kiini cha tatu, kuna namba 23,658 tena, mshale huo unaoelezea tarakimu 6, ukiiweka alama ya mamia. Ya 5 pia imesisitizwa katika kiini hiki.Mstari mmoja chini, kiini cha kwanza kinasema: “Hatua ya 3. Je, tarakimu hii ni kubwa kuliko au sawa na 5? Ndiyo-ongeza 1 kwa tarakimu katika thamani ya mahali fulani. Hapana—usibadilishe tarakimu katika thamani ya mahali uliyopewa.” Katika kiini cha pili, maagizo yanasema: “Ongeza 1 hadi 6 mahali pa mamia, kwa kuwa 5 ni kubwa kuliko au sawa na 5.” Kiini cha tatu kina namba 23,658 tena, na mshale unaoelezea tarakimu 6 na maandishi “ongeza 1”. Pia kuna bracket ya curly chini ya tarakimu 5 na 8, na mshale unaowaelezea na maandiko “kuchukua nafasi na 0s.”Katika mstari wa chini, kiini cha kwanza kinasema: “Hatua ya 4. Badilisha nafasi ya tarakimu zote kwa haki ya thamani ya mahali iliyotolewa na zero. Hivyo, 23,700 ni mviringo kwa mia karibu.” Katika kiini cha pili, maagizo yanasema: “Weka tarakimu zote kwa haki ya mahali pa mamia na zero.” Kiini cha tatu kina idadi 23,700, ambayo tumefikia kwa kuzunguka namba 23,658 hadi mia ya karibu.

    Zoezi\(\PageIndex{11}\)

    Pande zote kwa mia karibu: 17,852.

    Jibu

    17,900

    Zoezi\(\PageIndex{12}\)

    Pande zote kwa mia karibu: 468,751.

    Jibu

    468,800

    PANDE ZOTE NAMBA NZIMA.
    1. Pata thamani ya mahali uliyopewa na uiangalie kwa mshale. Nambari zote upande wa kushoto wa mshale hazibadilika.
    2. Weka tarakimu kwa haki ya thamani ya mahali.
    3. Je, tarakimu hii ni kubwa kuliko au sawa na 5?
      • Ndiyo-ongeza 11 kwa tarakimu katika thamani ya mahali fulani.
      • Hapana-usibadilishe tarakimu katika thamani ya mahali uliyopewa.
    4. Badilisha nafasi ya tarakimu zote kwa haki ya thamani ya mahali iliyotolewa na zero.
    Zoezi\(\PageIndex{13}\)

    Pande zote 103,978103,978 kwa karibu:

    1. mia
    2. elfu
    3. elfu kumi
    Jibu
    1.
    Machapisho mamia mahali katika 103,978. .
    Weka tarakimu kwa haki ya mahali pa mamia. .
    Tangu 7 ni kubwa kuliko au sawa na 5, kuongeza 1 kwa 9. Badilisha nafasi ya tarakimu zote kwa haki ya mahali mamia na zero. .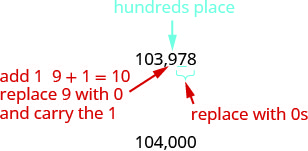
      Kwa hiyo, 104,000 ni 103,978 iliyozunguka kwa mia karibu.
    2.
    Machapisho maelfu mahali na kusisitiza tarakimu na haki ya maelfu mahali. .
    Tangu 9 ni kubwa kuliko au sawa na 5, kuongeza 1 kwa 3. Badilisha nafasi ya tarakimu zote kwa haki ya mahali mamia na zero. .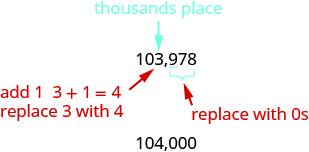
      Kwa hiyo, 104,000 ni 103,978 iliyozunguka kwa elfu ya karibu.
    3.
    Pata mahali pa maelfu kumi na usisitize tarakimu na haki ya mahali pa maelfu kumi. .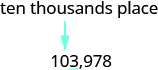
    Kwa kuwa 3 ni chini ya 5, tunaondoka 0 kama ilivyo, na kisha kuchukua nafasi ya tarakimu kwa haki na zero. .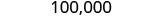
      Kwa hiyo, 100,000 ni 103,978 iliyozunguka kwa karibu elfu kumi.
    Zoezi\(\PageIndex{14}\)

    Pande zote 206,981 kwa karibu: 1. mia 2. elfu 3. elfu kumi.

    Jibu
    1. 207,000
    2. 207,000
    3. 210,000
    Zoezi\(\PageIndex{15}\)

    Pande zote 784,951 kwa karibu: 1. mia 2. elfu 3. elfu kumi.

    Jibu
    1. 785,000
    2. 785,000
    3. 780,000

    Tambua Mizigo na Tumia Vipimo vya mgawanyiko

    Nambari 2, 4, 6, 8, 10, na 12 huitwa wingi wa 2. nyingi ya 2 inaweza kuandikwa kama bidhaa ya idadi kuhesabu na 2.

    Mchoro uliofanywa na safu mbili za namba. Mstari wa juu unasoma “2, 4, 6, 8, 10, 12,” ikifuatiwa na elipsis. Chini ya 2 ni mara 2 1, chini ya 4 ni mara 2, chini ya 6 ni mara 2 3, chini ya 8 ni mara 2 4, chini ya 10 ni mara 2 5, na chini ya 12 ni mara 2 6.
    Kielelezo\(\PageIndex{4}\)

    Vile vile, nyingi ya 3 itakuwa bidhaa ya idadi ya kuhesabu na 3.

    Mchoro uliofanywa na safu mbili za namba. Mstari wa juu unasoma “3, 6, 9, 12, 15, 18,” ikifuatiwa na elipsis. Chini ya 3 ni mara 3 1, chini ya 6 ni mara 3 2, chini ya 9 ni mara 3, chini ya 12 ni mara 3 4, chini ya 15 ni mara 3 5, na chini ya 18 ni mara 3 6.
    Kielelezo\(\PageIndex{5}\)

    Tunaweza kupata wingi wa idadi yoyote kwa kuendelea na mchakato huu.

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Multiples” zitakusaidia kuendeleza uelewa bora wa wingi.

    Jedwali\(\PageIndex{1}\) linaonyesha wingi wa 2 kwa njia ya 9 kwa namba za kwanza za kuhesabu 12.

    Idadi ya Kuhesabu 1 2 3 4 5 6 7 8 9 10 11 12
    Wingi wa 2 2 4 6 8 10 12 14 16 18 20 22 24
    Wingi wa 3 3 6 9 12 15 18 21 24 27 30 33 36
    Wingi wa 4 4 8 12 16 20 24 28 32 36 40 44 48
    Wingi wa 5 5 10 15 20 25 30 35 40 45 50 55 60
    Wingi wa 6 6 12 18 24 30 36 42 48 54 60 66 72
    Wingi wa 7 7 14 21 28 35 42 49 56 63 70 77 84
    Wingi wa 8 8 16 24 32 40 48 56 64 72 80 88 96
    Wingi wa 9 9 18 27 36 45 54 63 72 81 90 99 108
    Wingi wa 10 10 20 30 40 50 60 70 80 90 100 110 120
    Jedwali\(\PageIndex{1}\)
    NYINGI YA IDADI

    idadi ni nyingi ya\(n\) kama ni bidhaa ya idadi kuhesabu na\(n\).

    Njia nyingine ya kusema kwamba 15 ni nyingi ya 3 ni kusema kwamba 15 ni mgawanyiko na 3. Hiyo ina maana kwamba wakati sisi kugawanya 3 katika 15, sisi kupata idadi kuhesabu. Kwa kweli,\(15\div 3\) ni 5, hivyo 15 ni\(5\cdot3\).

    KUGAWANYIKA NA IDADI

    Kama idadi\(m\) ni nyingi ya\(n\), basi\(m\) ni mgawanyiko na\(n\)

    Angalia wingi wa\(5\) katika Jedwali\(\PageIndex{1}\). Wote huisha katika 5 au 0. Hesabu zilizo na tarakimu ya mwisho ya 5 au 0 zinagawanyika na 5. Kuangalia mifumo mingine katika Jedwali\(\PageIndex{1}\) inayoonyesha wingi wa namba 2 kwa njia ya 9, tunaweza kugundua vipimo vya mgawanyiko zifuatazo:

    VIPIMO VYA UGAWANYIKO

    Nambari inagawanyika na:

    • 2 ikiwa tarakimu ya mwisho ni 0, 2, 4, 6, au 8.
    • 3 ikiwa jumla ya tarakimu inagawanyika na 3.
    • 5 ikiwa tarakimu ya mwisho ni 5 au 0.
    • 6 ikiwa inagawanyika na 2 na 3.
    • 10 ikiwa inaisha na 0.
    Zoezi\(\PageIndex{16}\)

    Je 5625 inagawanyika na 2? By 3? By 5? By 6? By 10?

    Jibu

    \[\begin{array} {ll} {\text{Is 5625 divisible by 2?}} &{} \\ {\text{Does it end in 0, 2, 4, 6, or 8?}} &{\text{No.}} \\ {} &{\text{5625 is not divisible by 2.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 3?}} &{} \\ {\text{What is the sum of the digits?}} &{5 + 6 + 2 + 5 = 18} \\ {\text{Is the sum divisible by 3?}} &{\text{Yes, 5625 is divisible by 3.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 5 or 10?}} &{} \\ {\text{What is the last digit? It is 5.}} &{\text{5625 is divisible by 5 but not by 10.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 6?}} &{} \\ {\text{Is it divisible by both 2 and 3?}} &{\text{No, 5625 is not divisible by 2, so 5625 is }} \\ {} &{\text{not divisible by 6.}}\end{array}\]

    Zoezi\(\PageIndex{17}\)

    Kuamua kama 4,962 inagawanyika na 2, na 3, na 5, na 6, na kwa 10.

    Jibu

    na 2, 3, na 6

    Zoezi\(\PageIndex{18}\)

    Kuamua kama 3,765 inagawanyika na 2, na 3, na 5, na 6, na kwa 10.

    Jibu

    na 3 na 5

    Kupata factorizations Mkuu na Multiples angalau kawaida

    Katika hisabati, mara nyingi kuna njia kadhaa za kuzungumza juu ya mawazo sawa. Hadi sasa, tumeona kwamba kama\(m\) ni nyingi ya\(n\), tunaweza kusema kwamba\(m\) ni mgawanyiko na\(n\). Kwa mfano, tangu 72 ni nyingi ya 8, tunasema 72 inagawanyika na 8. Tangu 72 ni nyingi ya 9, tunasema 72 ni mgawanyiko na 9. Tunaweza kueleza hii bado njia nyingine.

    Tangu\(8\cdot 9=72\), tunasema kwamba 8 na 9 ni sababu za 72. Tunapoandika\(72=8\cdot 9\), tunasema tuna factored 72.

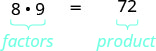
    Picha inaonyesha equation 8 mara 9 sawa 72. Imeandikwa chini ya maneno 8 mara 9 ni bracket curly na neno “sababu” wakati imeandikwa chini 72 ni bracket usawa na neno “bidhaa”.
    Kielelezo\(\PageIndex{6}\)

    Njia nyingine za kuzingatia 72 ni\(1\cdot 72\)\(2\cdot 36\),\(3\cdot 24\),\(4\cdot 18\) na\(6\cdot 12\). Sabini na mbili ina mambo mengi: 1, 2, 3, 4, 6, 8, 9, 12, 18, 36, na 72.

    SABABU

    Ikiwa\(a\cdot b=m\), basi\(a\) na\(b\) ni sababu za\(m\).

    Nambari zingine, kama 72, zina mambo mengi. Nambari nyingine zina sababu mbili tu.

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Kuzidisha Model na Factoring” itasaidia kuendeleza uelewa bora wa kuzidisha na kuzingatia.

    NAMBARI KUU NA IDADI YA VIPENGELE

    Nambari kuu ni namba ya kuhesabu zaidi ya 1, ambayo sababu zake pekee ni 1 na yenyewe.

    Nambari ya composite ni namba ya kuhesabu ambayo si mkuu. Nambari ya composite ina mambo mengine zaidi ya 1 na yenyewe.

    Kumbuka

    Kufanya shughuli za Hisabati za Manipulative “Hesabu Mkuu” zitakusaidia kuendeleza uelewa bora wa idadi kuu.

    Nambari za kuhesabu kutoka 2 hadi 19 zimeorodheshwa kwenye Kielelezo\(\PageIndex{7}\), na mambo yao. Hakikisha kukubaliana na lebo ya “mkuu” au “Composite” kwa kila mmoja!

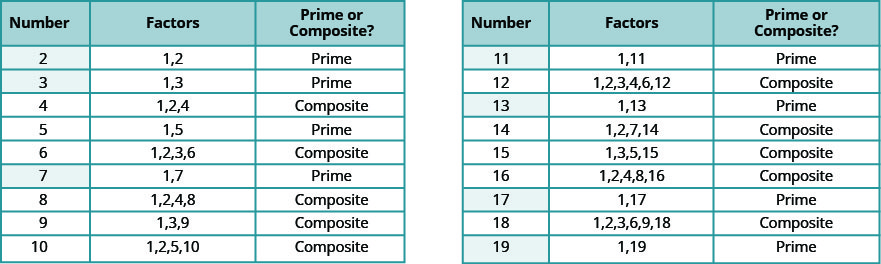
    Jedwali linaonyeshwa kwa safu kumi na moja na nguzo saba. Mstari wa kwanza ni mstari wa kichwa, na kila kiini huandika yaliyomo kwenye safu chini yake. Katika mstari wa kichwa, seli tatu za kwanza zinasoma kutoka kushoto kwenda kulia “Nambari”, “Mambo”, na “Mkuu au Composite?” Safu nzima ya nne ni tupu. Siri tatu za mwisho zinasoma kutoka kushoto kwenda kulia “Nambari”, “Factor”, na “Mkuu au Composite?” tena. Katika kila mstari unaofuata, kiini cha kwanza kina idadi, pili ina mambo yake, na ya tatu inaonyesha kama namba ni ya kwanza au composite. Nguzo tatu upande wa kushoto wa safu tupu katikati zina habari hii kwa namba 2 hadi 10, na nguzo tatu upande wa kulia wa safu ya kati tupu zina habari hii kwa namba 11 hadi 19. Kwenye upande wa kushoto wa safu tupu, katika mstari wa kwanza chini ya mstari wa kichwa, seli zinasoma kutoka kushoto kwenda kulia: “2", “1,2”, na “Mkuu”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “3", “1,3", na “Mkuu”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “4", “1,2,4", na “Composite”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “5", “1,5”, na “Mkuu”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “6", “1,2,3,6" na “Composite”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “7”, “1,7", na “Mkuu”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “8", “1,2,4,8", na “Composite”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “9", “1,3,9", na “Composite”. Katika mstari wa chini, seli zinasoma kutoka kushoto kwenda kulia: “10", “1,2,5,10", na “Composite”. Kwenye upande wa kulia wa safu tupu, katika mstari wa kwanza chini ya mstari wa kichwa, seli zinasoma kutoka kushoto kwenda kulia: “11", “1,11", na “Mkuu”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “12", “1,2,3,4,6,12", na “Composite”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “13", “1,13", na “Mkuu”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia “14", “1,2,7,14", na “Composite”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “15", “1,3,5,15", na “Composite”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia: “16", “1,2,4,8,16”, na “Composite”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia, “17", “1,17", na “Mkuu”. Katika mstari unaofuata, seli zinasoma kutoka kushoto kwenda kulia, “18", “1,2,3,6,9,18”, na “Composite”. Katika mstari wa chini, seli zinasoma kutoka kushoto kwenda kulia: “19", “1,19", na “Mkuu”.
    Kielelezo\(\PageIndex{7}\)

    Nambari kuu ni chini ya 20 ni 2, 3, 5, 7, 11, 13, 17, na 19. Kumbuka kwamba tu hata mkuu idadi ni 2.

    Nambari ya composite inaweza kuandikwa kama bidhaa ya kipekee ya primes. Hii inaitwa factorization mkuu wa idadi. Kupata factorization mkuu wa idadi Composite itakuwa muhimu baadaye katika kozi hii.

    MKUU FACTORIZATION

    Factorization mkuu wa idadi ni bidhaa ya idadi ya mkuu ambayo ni sawa na idadi.

    Ili kupata factorization kuu ya nambari ya composite, pata mambo mawili ya nambari na uitumie kuunda matawi mawili. Kama sababu ni mkuu, tawi hilo ni kamili. Circle kwamba mkuu!

    Ikiwa sababu sio mkuu, pata sababu mbili za nambari na uendelee mchakato. Mara baada ya matawi yote yamezunguka primes mwishoni, factorization imekamilika. Nambari ya composite sasa inaweza kuandikwa kama bidhaa ya namba kuu.

    Zoezi\(\PageIndex{19}\)

    Sababu 48.

    Jibu

    Takwimu hii ni meza ambayo ina nguzo tatu na safu nne. Safu ya kwanza ni safu ya kichwa, na ina majina na namba za kila hatua. Safu ya pili ina maelekezo zaidi yaliyoandikwa na baadhi ya hesabu. Safu ya tatu ina kazi nyingi za hesabu zinazohusiana na hatua zilizoandikwa na maelekezo. Katika mstari wa juu, kiini cha kwanza kinasema: “Hatua ya 1. Pata mambo mawili ambayo bidhaa ni nambari iliyotolewa. Tumia namba hizi kuunda matawi mawili.” Kiini cha pili kina equation ya algebraic 48 sawa na mara 2 24. Katika kiini cha tatu, kuna mti wa sababu na 48 juu. Matawi mawili yanatoka 48 na kusitisha saa 2 na 24 kwa mtiririko huo.Mstari mmoja chini, maagizo katika kiini cha kwanza husema: “Hatua ya 2. Kama sababu ni mkuu, tawi hilo ni kamili. Circle mkuu.” Katika kiini cha pili, maagizo yanasema: “2 ni mkuu. Circle mkuu.” Katika kiini cha tatu, mti wa sababu kutoka hatua ya 1 unarudiwa, lakini 2 chini ya mti sasa huzunguka.Mstari mmoja chini, kiini cha kwanza kinasema: “Hatua ya 3. Kama sababu si mkuu, kuandika kama bidhaa ya mambo mawili na kuendelea na mchakato.” Katika kiini cha pili, maagizo yanasema: “24 sio mkuu. Kuvunja ndani ya mambo mawili zaidi.” Kiini cha tatu kina mti wa asili, na 48 juu na matawi mawili ya kushini-akizungumzia yanayotokana na 2, ambayo imesisitizwa, na 24. Matawi mawili zaidi yanatoka 24 na kusitisha saa 4 na 6 kwa mtiririko huo. Mstari mmoja chini, maelekezo katikati ya kiini husema “4 na 6 sio mkuu. Kuvunja kila mmoja katika mambo mawili. Katika kiini upande wa kulia, mti wa sababu hurudiwa tena. Matawi mawili yanashuka kutoka 4 na kusitisha saa 2 na 2. Wote 2s huzunguka. Matawi mawili zaidi hutoka kutoka 6 na kusitisha saa 2 na a 3, ambazo zote mbili zimezunguka. Maagizo upande wa kushoto yanasema “2 na 3 ni mkuu, hivyo uwazunguze.”Katika mstari wa chini, kiini cha kwanza kinasema: “Hatua ya 4. Andika namba ya vipande kama bidhaa za primes zote zilizozunguka.” Kiini cha pili kinaachwa tupu. Kiini cha tatu kina equation ya algebraic 48 sawa mara 2 mara 2 mara 2 mara 3.

    Tunasema\(2\cdot 2\cdot 2\cdot 2\cdot 3\) ni factorization mkuu wa 48. Kwa ujumla tunaandika primes katika utaratibu wa kupanda. Hakikisha kuzidisha mambo ili kuthibitisha jibu lako!

    Kama sisi kwanza factored 48 kwa njia tofauti, kwa mfano kama\(6\cdot 8\), matokeo bado kuwa sawa. Kumaliza factorization mkuu na uhakikishe hili mwenyewe.

    Zoezi\(\PageIndex{20}\)

    Kupata factorization mkuu wa 80.

    Jibu

    \(2\cdot 2\cdot 2\cdot 2\cdot 5\)

    Zoezi\(\PageIndex{21}\)

    Kupata factorization mkuu wa 60.

    Jibu

    \(2\cdot 2\cdot 3\cdot 5\)

    KUPATA FACTORIZATION MKUU WA IDADI COMPOSITE.
    1. Pata mambo mawili ambayo bidhaa ni nambari iliyotolewa, na utumie namba hizi kuunda matawi mawili.
    2. Kama sababu ni mkuu, tawi hilo ni kamili. Circle mkuu, kama bud juu ya mti.
    3. Ikiwa jambo sio mkuu, andika kama bidhaa ya mambo mawili na uendelee mchakato.
    4. Andika nambari ya composite kama bidhaa ya primes zote zilizozunguka.
    Zoezi\(\PageIndex{22}\)

    Kupata factorization mkuu wa 252.

    Jibu
    Hatua ya 1. Pata sababu mbili ambazo bidhaa zake ni 252. 12 na 21 sio mkuu.

    Kuvunja 12 na 21 katika mambo mawili zaidi. Endelea mpaka primes zote zimezingatiwa.    		 .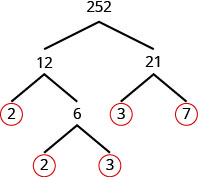
    Hatua ya 2. Andika 252 kama bidhaa ya primes zote zilizozunguka.

    \(252=2\cdot 2\cdot 3\cdot 3\cdot 7\)
    Zoezi\(\PageIndex{23}\)

    Kupata factorization mkuu wa 126.

    Jibu

    \(2\cdot 3\cdot 3\cdot 7\)

    Zoezi\(\PageIndex{24}\)

    Kupata factorization mkuu wa 294.

    Jibu

    \(2\cdot 3\cdot 7\cdot 7\)

    Moja ya sababu tunayoangalia wingi na primes ni kutumia mbinu hizi ili kupata idadi ndogo ya kawaida ya namba mbili. Hii itakuwa na manufaa wakati sisi kuongeza na Ondoa sehemu na denominator tofauti s Mbinu mbili hutumiwa mara nyingi kupata angalau kawaida nyingi na tutaangalia wote wawili.

    Njia ya kwanza ni Njia ya Kuorodhesha Multiples. Ili kupata nyingi ya kawaida ya 12 na 18, tunaandika orodha ya kwanza ya 12 na 18:

    Safu mbili za namba zinaonyeshwa. Mstari wa kwanza huanza na 12, ikifuatiwa na koloni, halafu 12, 24, 36, 48, 60, 72, 84, 96, 108, na elipsis. 36, 72, na 108 zimeandikwa kwa ujasiri. Mstari wa pili huanza na 18, ikifuatiwa na koloni, kisha 18, 36, 54, 72, 90, 108, na elipsis. Tena, namba 36, 72, na 108 zimeandikwa kwa ujasiri. Katika mstari hapa chini ni maneno “Mizigo ya kawaida”, koloni na namba 36, 72, na 108, zilizoandikwa kwa nyekundu. Mstari mmoja hapa chini ni maneno “Multiple Multiple Common”, koloni na namba 36, iliyoandikwa kwa bluu.
    Kielelezo\(\PageIndex{8}\)

    Kumbuka kwamba baadhi ya idadi kuonekana katika orodha zote mbili. Wao ni wingi wa kawaida wa 12 na 18.

    Tunaona kwamba machache ya kwanza ya kawaida ya 12 na 18 ni 36, 72, na 108. Tangu 36 ni ndogo zaidi ya mafungu ya kawaida, tunaiita kuwa nyingi zaidi. Mara nyingi tunatumia LCM ya kifupi.

    ANGALAU YA KAWAIDA NYINGI

    Nyingi ya kawaida (LCM) ya namba mbili ni idadi ndogo zaidi ambayo ni nyingi ya namba zote mbili.

    Sanduku la utaratibu linaorodhesha hatua za kuchukua ili kupata LCM kwa kutumia njia kuu ya mambo tuliyotumia hapo juu kwa 12 na 18.

    KUPATA ANGALAU YA KAWAIDA NYINGI KWA ORODHA VINGI.
    1. Andika orodha kadhaa za kila nambari.
    2. Angalia kwa idadi ndogo ambayo inaonekana katika orodha zote mbili.
    3. Nambari hii ni LCM.
    Zoezi\(\PageIndex{25}\)

    Kupata angalau kawaida nyingi ya 15 na 20 na orodha ya mafungu.

    Jibu
    Fanya orodha ya mafungu machache ya kwanza ya 15 na ya 20, na uitumie ili kupata angalau ya kawaida. .
    Angalia kwa idadi ndogo ambayo inaonekana katika orodha zote mbili. Nambari ya kwanza kuonekana kwenye orodha zote mbili ni 60, hivyo 60 ni nyingi ya kawaida ya 15 na 20.

    Kumbuka kwamba 120 ni katika orodha zote mbili, pia. Ni nyingi ya kawaida, lakini si angalau ya kawaida nyingi.

    Zoezi\(\PageIndex{26}\)

    Kupata angalau ya kawaida nyingi kwa orodha nyingi: 9 na 12.

    Jibu

    \(36\)

    Zoezi\(\PageIndex{27}\)

    Kupata angalau ya kawaida nyingi kwa orodha nyingi: 18 na 24.

    Jibu

    \(72\)

    Njia yetu ya pili ya kupata idadi ndogo ya kawaida ya namba mbili ni kutumia Njia ya Mambo Mkuu. Hebu tupate LCM ya 12 na 18 tena, wakati huu kwa kutumia sababu zao kuu.

    Zoezi\(\PageIndex{28}\)

    Kupata angalau Common Multiple (LCM) ya 12 na 18 kwa kutumia mkuu sababu mbinu.

    Jibu

    Takwimu hii ni meza ambayo ina nguzo tatu na safu nne. Safu ya kwanza ni safu ya kichwa, na ina majina na namba za kila hatua. Safu ya pili ina maelekezo zaidi yaliyoandikwa na baadhi ya hesabu. Safu ya tatu ina kazi nyingi za hesabu zinazohusiana na hatua zilizoandikwa na maelekezo. Katika mstari wa juu, kiini cha kwanza kinasema: “Hatua ya 1. Andika kila namba kama bidhaa ya primes.” Kiini cha pili kinaachwa tupu. Katika kiini cha tatu, kuna miti miwili ya sababu. Katika mti wa kwanza, matawi mawili yanatoka 18 na kukomesha saa 3 na 6 kwa mtiririko huo. Ya 3 ni mkuu na kwa hiyo ikizunguka. Matawi mawili zaidi yanashuka kutoka 6 na kusitisha katika 2 na 3, yote ambayo yanazunguka. Katika mti wa pili wa mti, matawi mawili yanatoka 12 na kukomesha saa 3 na 4. Ya 3 imezungukwa. Matawi mawili zaidi hutoka kutoka 4, kukomesha saa 2 na 2, yote ambayo yanazunguka.Mstari mmoja chini, maagizo katika kiini cha kwanza husema: “Hatua ya 2. Orodha ya primes ya kila idadi. Mechi primes wima ikiwezekana.” Katika kiini cha pili, maagizo yanasema: “Orodha ya primes ya 12. Orodha ya primes ya 18. Line up na primes ya 12 iwezekanavyo. Kama si kujenga safu mpya.” Kiini cha tatu kina factorization mkuu wa 12 imeandikwa kama equation 12 sawa mara 2 mara 3. Chini equation hii ni mwingine kuonyesha factorization mkuu wa 18 imeandikwa kama equation 18 sawa 2 mara 3 mara 3. equations mbili line up wima kwa ishara sawa. Ya kwanza 2 katika factorization mkuu wa 12 inalingana na 2 katika factorization mkuu wa 18. Chini ya pili 2 katika factorization mkuu wa 12 ni pengo katika factorization mkuu wa 18. Chini ya 3 katika factorization mkuu wa 12 ni ya kwanza 3 katika factorization mkuu wa 18. Ya pili 3 katika factorization mkuu haina sababu juu yake kutoka factorization mkuu wa 12.Mstari mmoja chini, maagizo katika kiini cha kwanza husema: “Weka nambari kutoka kila safu.” Kiini cha pili ni tupu. Kiini cha tatu kina factorizations mkuu wa 12 na 18 tena, mfano kama equations mbili iliyokaa kama ilivyokuwa kabla. Wakati huu, mstari wa usawa unafanywa chini ya factorization kuu ya 18. Chini ya mstari huu ni equation LCM sawa na mara 2 mara 2 mara 3. Mishale ni inayotolewa chini wima kutoka factorization mkuu wa 12 kwa njia ya factorization mkuu wa 18 kuishia katika LCM equation. Mshale wa kwanza huanza saa ya kwanza 2 katika factorization mkuu wa 12 na inaendelea chini kupitia 2 katika factorization mkuu wa 18, kuishia na 2 kwanza katika LCM. Mshale wa pili huanza saa 2 ijayo katika factorization mkuu wa 12 na inaendelea chini kupitia pengo katika factorization mkuu wa 18, kuishia na pili 2 katika LCM. Mshale wa tatu huanza saa 3 katika factorization mkuu wa 12 na inaendelea chini kupitia kwanza 3 katika factorization mkuu wa 18, kuishia na kwanza 3 katika LCM. Mshale wa mwisho huanza saa ya pili ya 3 katika factorization mkuu wa 18 na inaonyesha chini ya pili 3 katika LCM.Katika mstari wa chini wa meza, kiini cha kwanza kinasema: “Hatua ya 4: Panua mambo.” Kiini cha pili ni benki. Kiini cha tatu kina equation LCM sawa 36.

    Kumbuka kwamba sababu kuu ya\(12(2\cdot 2\cdot 3)\) na sababu mkuu wa\(18(2\cdot 3\cdot 3)\) ni pamoja na katika LCM\((2\cdot 2\cdot 3\cdot 3)\). Hivyo 36 ni angalau kawaida nyingi ya 12 na 18.

    Kwa kulinganisha juu ya primes ya kawaida, kila sababu ya kawaida ya kawaida hutumiwa mara moja tu. Kwa njia hii una uhakika kwamba 36 ni angalau kawaida nyingi.

    Zoezi\(\PageIndex{29}\)

    Pata LCM kwa kutumia njia kuu ya mambo: 9 na 12.

    Jibu

    \(36\)

    Zoezi\(\PageIndex{30}\)

    Kupata LCM kutumia mkuu sababu mbinu: 18 na 24.

    Jibu

    \(72\)

    KUPATA ANGALAU KAWAIDA NYINGI KWA KUTUMIA MKUU SABABU MBINU.
    1. Andika kila nambari kama bidhaa ya primes.
    2. Orodha ya primes ya kila idadi. Mechi primes wima ikiwezekana.
    3. Kuleta chini nguzo.
    4. Panua mambo.
    Zoezi\(\PageIndex{31}\)

    Kupata angalau Common Multiple (LCM) ya 24 na 36 kwa kutumia mkuu sababu mbinu.

    Jibu
    Kupata primes ya 24 na 36.
    Mechi primes wima ikiwezekana.

    Kuleta chini nguzo zote.    		 .
    Panua mambo. .
     

    LCM ya 24 na 36 ni 72.
    Zoezi\(\PageIndex{32}\)

    Kupata LCM kutumia mkuu sababu mbinu: 21 na 28.

    Jibu

    \(84\)

    Zoezi\(\PageIndex{33}\)

    Kupata LCM kutumia mkuu sababu mbinu: 24 na 32.

    Jibu

    \(96\)

    Kumbuka

    Fikia rasilimali hii ya mtandaoni kwa maelekezo ya ziada na mazoezi kwa kutumia namba nzima. Utahitaji kuwezesha Java kwenye kivinjari chako cha wavuti ili utumie programu.

    Dhana muhimu

    • Mahali Thamani kama katika Kielelezo.
    • Jina Nambari Nzima katika Maneno
      1. Anza upande wa kushoto na jina namba katika kila kipindi, ikifuatiwa na jina la kipindi.
      2. Weka koma katika nambari ili kutenganisha vipindi.
      3. Je, si jina la kipindi hicho.
    • Andika Nambari Nzima Kutumia Tarakimu
      1. Tambua maneno yanayoonyesha vipindi. (Kumbuka kipindi hicho kamwe jina lake.)
      2. Chora vifungo 3 ili kuonyesha idadi ya maeneo inahitajika kila kipindi. Toa vipindi kwa commas.
      3. Jina namba katika kila kipindi na uweke tarakimu katika nafasi sahihi ya thamani ya mahali.
    • Nambari nzima ya pande zote
      1. Pata thamani ya mahali uliyopewa na uiangalie kwa mshale. Nambari zote upande wa kushoto wa mshale hazibadilika.
      2. Weka tarakimu kwa haki ya thamani ya mahali.
      3. Je, tarakimu hii ni kubwa kuliko au sawa na 5?
        • Ndiyo-ongeza 1 kwa tarakimu katika thamani ya mahali fulani.
        • Hapana-usibadilishe tarakimu katika thamani ya mahali uliyopewa.
      4. Badilisha nafasi ya tarakimu zote kwa haki ya thamani ya mahali iliyotolewa na zero.
    • Mgawanyiko Uchunguzi: idadi ni mgawanyiko na:
      • 2 ikiwa tarakimu ya mwisho ni 0, 2, 4, 6, au 8.
      • 3 ikiwa jumla ya tarakimu inagawanyika na 3.
      • 5 ikiwa tarakimu ya mwisho ni 5 au 0.
      • 6 ikiwa inagawanyika na 2 na 3.
      • 10 ikiwa inaisha na 0.
    • Kupata Factorization Mkuu wa Idadi Composite
      1. Pata mambo mawili ambayo bidhaa ni nambari iliyotolewa, na utumie namba hizi kuunda matawi mawili.
      2. Kama sababu ni mkuu, tawi hilo ni kamili. Circle mkuu, kama bud juu ya mti.
      3. Ikiwa jambo sio mkuu, andika kama bidhaa ya mambo mawili na uendelee mchakato.
      4. Andika nambari ya composite kama bidhaa ya primes zote zilizozunguka.
    • Pata Multiples Multiple kwa Orodha Multiples
      1. Andika orodha kadhaa za kila nambari.
      2. Angalia kwa idadi ndogo ambayo inaonekana katika orodha zote mbili.
      3. Nambari hii ni LCM.
    • Pata Multiple Multiple Kutumia Njia ya Mambo Mkuu
      1. Andika kila nambari kama bidhaa ya primes.
      2. Orodha ya primes ya kila idadi. Mechi primes wima ikiwezekana.
      3. Kuleta chini nguzo.
      4. Panua mambo.

    faharasa

    idadi ya vipengele
    Nambari ya composite ni namba ya kuhesabu ambayo si mkuu. Nambari ya composite ina mambo mengine zaidi ya 1 na yenyewe.
    kuhesabu idadi
    Nambari za kuhesabu ni namba 1, 2, 3,...
    kugawanyika kwa idadi
    Kama idadi\(m\) ni nyingi ya\(n\), basi\(m\) ni mgawanyiko na\(n\). (Kama 6 ni nyingi ya 3, basi 6 ni mgawanyiko na 3.)
    mambo
    Ikiwa\(a\cdot b=m\), basi\(a\) na\(b\) ni sababu za\(m\). Tangu\(3 \cdot 4 = 12\), basi 3 na 4 ni sababu za 12.
    angalau ya kawaida nyingi
    Nambari ndogo ya kawaida ya namba mbili ni namba ndogo zaidi ambayo ni nyingi ya namba zote mbili.
    nyingi ya idadi
    idadi ni nyingi ya\(n\) kama ni bidhaa ya idadi kuhesabu na\(n\).
    nambari ya mstari
    Mstari wa nambari hutumiwa kutazama namba. Idadi kwenye mstari wa nambari hupata kubwa kama wanaenda kutoka kushoto kwenda kulia, na ndogo kama wanaenda kutoka kulia kwenda kushoto.
    asili
    Asili ni hatua iliyoandikwa 0 kwenye mstari wa namba.
    factorization mkuu
    Factorization mkuu wa idadi ni bidhaa ya idadi ya mkuu ambayo ni sawa na idadi.
    nambari kuu
    Nambari kuu ni namba ya kuhesabu zaidi ya 1, ambayo sababu zake pekee ni 1 na yenyewe.
    idadi nzima
    Nambari nzima ni namba 0, 1, 2, 3,...