17.4: Ufumbuzi wa Mfululizo wa Ulinganisho tofauti

Malengo ya kujifunza

• Tumia mfululizo wa nguvu ili kutatua equations ya kwanza na ya pili ya utaratibu tofauti.

Hapo awali, tulijifunza jinsi kazi zinaweza kuwakilishwa kama mfululizo wa nguvu,\(\displaystyle y(x)=\sum_{n=0}^{\infty} a_nx^n\). Pia tuliona kwamba tunaweza kupata uwakilishi wa mfululizo wa derivatives ya kazi hizo kwa kutofautisha muda wa mfululizo wa nguvu kwa muda. Hii inatoa

\[y′(x)=\sum_{n=1}^{\infty}na_nx^{n−1} \nonumber \]

na

\[y″(x)=\sum_{n=2}^{\infty}n(n−1)a_nx^{n−2}. \nonumber \]

Katika hali nyingine, uwakilishi wa mfululizo wa nguvu unaweza kutumika kupata ufumbuzi wa equations tofauti.

Mifano na mazoezi katika sehemu hii zilichaguliwa kwa ufumbuzi wa nguvu uliopo. Hata hivyo, si mara zote kesi kwamba ufumbuzi wa nguvu zipo. Wale wenu wanaopenda matibabu ya ukali zaidi ya mada hii wanapaswa kuchunguza sehemu ya usawa tofauti ya LibreTexts.

Mkakati wa Kutatua matatizo: Kutafuta Ufumbuzi wa Mfululizo wa Nguvu kwa usawa tofauti

1. Fikiria equation tofauti ina suluhisho la fomu\[y(x)=\sum_{n=0}^{\infty}a_nx^n. \nonumber \]
2. Tofautisha mfululizo wa nguvu mrefu kwa muda ili kupata\[y′(x)=\sum_{n=1}^{\infty}na_nx^{n−1} \nonumber \] na\[y″(x)=\sum_{n=2}^{\infty}n(n−1)a_nx^{n−2}. \nonumber \]
3. Badilisha maneno ya mfululizo wa nguvu katika usawa tofauti.
4. Re-index kiasi kama muhimu kuchanganya maneno na kurahisisha kujieleza.
5. Equate coefficients ya nguvu kama ya\(x\) kuamua maadili kwa coefficients\(a_n\) katika mfululizo nguvu.
6. Badilisha coefficients nyuma katika mfululizo wa nguvu na uandike suluhisho.

Mfano\(\PageIndex{1}\): Series Solutions to Differential Equations

Pata ufumbuzi wa mfululizo wa nguvu kwa equations tofauti zifuatazo.

1. \(y''−y=0\)
2. \((x^2−1)y″+6xy′+4y=−4\)

Suluhisho

Sehemu ya

Kudhani

\[y(x)=\sum_{n=0}^{∞}a_nx^n \tag{step 1} \]

Kisha,

\[y′(x)=\sum_{n=1}^{∞}na_nx^{n−1} \tag{step 2A} \]

na

\[y″(x)=\sum_{n=2}^{∞}n(n−1)a_nx^{n−2} \tag{step 2B} \]

Tunataka kupata maadili kwa coefficients\(a_n\) vile

\[\begin{align*} &y″−y =0 \\[4pt] &\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}−\sum_{n=0}^{∞}a_nx^n =0 \tag{step 3}. \end{align*} \]

Tunataka fahirisi za jumla zetu zifanane ili tuweze kuzieleza kwa kutumia summation moja. Hiyo ni, tunataka kuandika upya summation ya kwanza ili ianze na\(n=0\).

Kwa re-index muda wa kwanza, kuchukua nafasi\(n\) na\(n+2\) ndani ya jumla, na mabadiliko ya chini summation kikomo kwa\(n=0.\) Sisi kupata

\[\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}=\sum_{n=0}^∞ (n+2)(n+1)a_{n+2}x^n. \nonumber \]

Hii inatoa

\[\begin{align*}\sum_{n=0}^{∞}(n+2)(n+1)a_{n+2}x^n−\sum_{n=0}^{∞}a_nx_n &=0 \\[4pt] \sum_{n=0}^{∞}[(n+2)(n+1)a_{n+2}−a_n]x^n &=0 \tag{step 4}.\end{align*} \]

Kwa sababu nguvu mfululizo upanuzi wa kazi ni ya kipekee, equation hii inaweza kuwa kweli tu kama coefficients ya kila nguvu ya\(x\) ni sifuri. Hivyo tuna

\[(n+2)(n+1)a_{n+2}−a_n=0 \text{ for }n=0,1,2,…. \nonumber \]

Uhusiano huu wa kurudia unatuwezesha kuelezea kila mgawo\(a_n\) kwa suala la mgawo wa maneno mawili mapema. Hii mavuno kujieleza moja kwa hata maadili ya\(n\) na kujieleza mwingine kwa maadili isiyo ya kawaida ya\(n\). Kuangalia kwanza katika milinganyo kuwashirikisha hata maadili ya\(n\), tunaona kwamba

\[\begin{align*}a_2 &= \dfrac{a_0}{2} \\[5pt] a_4 &= \dfrac{a_2}{4⋅3} = \dfrac{a_0}{4!}\\[5pt] a_6 &= \dfrac{a_4}{6⋅5} =\dfrac{a_0}{6!} \\ &\qquad ⋮ \end{align*}\]

Hivyo, kwa ujumla, wakati\(n\) ni hata,

\[a_n=\dfrac{a_0}{n!}. \tag{step 5} \]

Kwa equations kuwashirikisha maadili isiyo ya kawaida ya\(n,\) tunaona kwamba

\[\begin{align*}a_3 &=\dfrac{a_1}{3⋅2}=\dfrac{a_1}{3!} \\[5pt] a_5 &= \dfrac{a_3}{5⋅4}=\dfrac{a_1}{5!} \\[5pt] a_7 &= \dfrac{a_5}{7⋅6}=\dfrac{a_1}{7!} \\ &\qquad ⋮ \end{align*}\]

Kwa hiyo, kwa ujumla, wakati\(n\) ni isiyo ya kawaida,

\[a_n=\dfrac{a_1}{n!}. \tag{step 5} \]

Kuweka hii pamoja, tuna

\[\begin{align*}y(x) &= \sum_{n=0}^{∞}a_nx^n \\[4pt] &=a_0+a_1x+\dfrac{a_0}{2}x^2+\dfrac{a_1}{3!}x^3+\dfrac{a_0}{4!}x^4+\dfrac{a_1}{5!}x^5+⋯. \end{align*}\]

Re-indexing kiasi kwa akaunti kwa maadili hata na isiyo ya kawaida ya\(n\) tofauti, sisi kupata

\[y(x)=a_0 \sum_{k=0}^{∞} \dfrac{1}{(2k)!}x^{2k}+a_1 \sum_{k=0}^{∞}\dfrac{1}{(2k+1)!}x^{2k+1}. \tag{step 6} \]

Uchambuzi kwa sehemu a.

Kama ilivyotarajiwa kwa pili ili tofauti equation, ufumbuzi huu inategemea constants mbili holela. Hata hivyo, kumbuka kuwa equation yetu tofauti ni equation tofauti ya mgawo wa mgawo, lakini ufumbuzi wa mfululizo wa nguvu hauonekani kuwa na fomu inayojulikana (iliyo na kazi za kielelezo) ambazo tunatumiwa kuona. Zaidi ya hayo, tangu\(y(x)=c_1e^x+c_2e^{−x}\) ni ufumbuzi wa jumla wa equation hii, ni lazima kuwa na uwezo wa kuandika ufumbuzi wowote katika fomu hii, na si wazi kama ufumbuzi nguvu mfululizo sisi tu kupatikana unaweza, kwa kweli, kuandikwa katika fomu hiyo.

Kwa bahati nzuri, baada ya kuandika uwakilishi nguvu mfululizo wa\(e^x\)\(e^{−x},\) na kufanya baadhi algebra, tunaona kwamba kama sisi kuchagua

\[c_0=\dfrac{(a_0+a_1)}{2}, c_1=\dfrac{(a_0−a_1)}{2}, \nonumber \]

sisi basi\(a_0=c_0+c_1\) na\(a_1=c_0−c_1,\) na

\[\begin{align*}y(x) &= a_0+a_1x+\dfrac{a_0}{2}x^2+\dfrac{a_1}{3!}x^3+\dfrac{a_0}{4!}x^4+\dfrac{a_1}{5!}x^5+⋯ \\[4pt] &=(c_0+c_1)+(c_0−c_1)x+\dfrac{(c_0+c_1)}{2}x^2+\dfrac{(c_0−c_1)}{3!}x^3+\dfrac{(c_0+c_1)}{4!}x^4+\dfrac{(c_0−c_1)}{5!}x^5+⋯\\[4pt] &=c_0 \sum_{n=0}^{∞} \dfrac{x^n}{n!}+c_1 \sum_{n=0}^{∞}\dfrac{(−x)^n}{n!} \\[4pt] &=c_0e^x+c_1e^{−x}.\end{align*}\]

Kwa hiyo tuna, kwa kweli, tumepata ufumbuzi huo wa jumla. Kumbuka kuwa uchaguzi huu wa\(c_1\) na\(c_2\) si dhahiri. Hii ni kesi wakati sisi kujua nini jibu lazima, na kuwa kimsingi “reverse-engineered” uchaguzi wetu wa coefficients.

Sehemu ya b

Kudhani

\[y(x)=\sum_{n=0}^{∞}a_nx^n \tag{step 1} \]

Kisha,

\[y′(x)=\sum_{n=1}^{∞}na_nx^{n−1} \tag{step 2} \]

na

\[y″(x)=\sum_{n=2}^{∞}n(n−1)a_nx^{n−2} \tag{step 2} \]

Tunataka kupata maadili kwa coefficients\(a_n\) vile

\[\begin{align*}(x^2−1)y″+6xy′+4y &=−4 \\ (x^2−1) \sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+6x \sum_{n=1}^{∞}na_nx^{n−1}+4 \sum_{n=0}^{∞}a_nx^n &=−4 \\[4pt] x^2 \sum_{n=2}^{∞} n(n−1)a_nx^{n−2}−\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+6x \sum_{n=1}^{∞}na_nx^{n−1}+4 \sum_{n=0}^{∞}a_nx^n &=−4. \end{align*}\]

Kuchukua mambo ya nje ndani ya summations, tunapata

\[\sum_{n=2}^{∞}n(n−1)a_nx^n−\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+\sum_{n=1}^∞ 6na_nx^n+ \sum_{n=0}^∞ 4a_nx^n=−4 \tag{step 3}. \]

Sasa, katika summation kwanza, tunaona kwamba wakati\(n=0\) au\(n=1\), mrefu kutathmini kwa sifuri, ili tuweze kuongeza masharti haya nyuma katika jumla yetu ya kupata

\[\sum_{n=2}^{∞}n(n−1)a_nx^n=\sum_{n=0}^∞ n(n−1)a_nx^n. \nonumber \]

Vile vile, katika muda wa tatu, tunaona kwamba wakati\(n=0\), kujieleza kutathmini kwa sifuri, ili tuweze kuongeza kwamba mrefu nyuma katika kama vizuri. Tuna

\[\sum_{n=1}^∞ 6na_nx^n=\sum_{n=0}^∞6na_nx^n. \nonumber \]

Kisha, tunahitaji tu kuhama fahirisi katika muda wetu wa pili. Tunapata

\[\sum_{n=2}^∞n(n−1)a_nx^{n−2}=\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n. \nonumber \]

Hivyo, tuna

\[\begin{align*} \sum_{n=0}^∞n(n−1)a_nx^n−\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n+\sum_{n=0}^∞6na_nx^n+\sum_{n=0}^∞4a_nx^n &=−4 \tag{step 4} \\[4pt] \sum_{n=0}^∞[n(n−1)a_n−(n+2)(n+1)a_{n+2}+6na_n+4a_n]x^n &=−4 \\[4pt] \sum_{n=0}^∞[(n^2−n)a_n+6na_n+4a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞[n^2a_n+5na_n+4a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞ [(n^2+5n+4)a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞[(n+4)(n+1)a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \end{align*} \]

Kuangalia coefficients ya kila nguvu ya\(x\), tunaona kwamba muda wa mara kwa mara lazima iwe sawa na\(−4\), na coefficients ya nguvu nyingine zote za\(x\) lazima zero. Kisha, kuangalia kwanza katika muda wa mara kwa mara,

\[\begin{aligned}4a_0−2a_2 &=−4 \\ a_2 &=2a_0+2 \end{aligned} \tag{step 3} \]

Kwa\(n≥1\), tuna

\[\begin{align*}(n+4)(n+1)a_n−(n+2)(n+1)a_{n+2} &= 0 \\[4pt] (n+1)[(n+4)a_n−(n+2)a_{n+2}] &=0. \end{align*}\]

Tangu\(n≥1, \; n+1≠0,\) tunaona kwamba

\[(n+4)a_n−(n+2)a_{n+2}=0 \nonumber \]

na hivyo

\[a_{n+2}=\dfrac{n+4}{n+2}a_n. \nonumber \]

Kwa maana hata maadili ya\(n\), tuna

\[\begin{align*} a_4 &=\dfrac{6}{4}(2a_0+2)=3a_0+3 \\ a_6 &= \dfrac{8}{6}(3a_0+3)=4a_0+4 \\[4pt] &\qquad ⋮ \end{align*}\]

Kwa ujumla,

\[a_{2k}=(k+1)(a_0+1). \tag{step 5} \]

Kwa maadili isiyo ya kawaida ya\(n,\) tuna

\[\begin{align*}a_3 &=\dfrac{5}{3}a_1 \\[4pt] a_5 &= \dfrac{7}{5}a_3=\dfrac{7}{3}a_1 \\[4pt] a_7 &=\dfrac{9}{7}a_5=\dfrac{9}{3} a_1=3a_1 \\[4pt] &\qquad ⋮ \end{align*}\]

Kwa ujumla,

\[a_{2k+1}=\dfrac{2k+3}{3}a_1. \tag{step 5 continued} \]

Kuweka hii pamoja, tuna

\[y(x)=\sum_{k=0}^∞ (k+1)(a_0+1)x^{2k}+\sum_{k=0}^∞ (\dfrac{2k+3}{3})a_1x^{2k+1}. \tag{step 6} \]

Zoezi\(\PageIndex{1}\)

Pata ufumbuzi wa mfululizo wa nguvu kwa equations tofauti zifuatazo.

1. \(y′+2xy=0\)
2. \((x+1)y′=3y\)

Kidokezo

Fuata mkakati wa kutatua matatizo.

Jibu

\(\displaystyle y(x)=a_0 \sum_{n=0}^∞ \dfrac{(−1)^n}{n!}x^{2n}=a_0e^{−x^2}\)

Jibu b

\(y(x)=a_0(x+1)^3\)

Kazi za Bessel

Tunakaribia sehemu hii kwa utangulizi mfupi wa kazi za Bessel. Matibabu kamili ya kazi za Bessel ni vizuri zaidi ya upeo wa kozi hii, lakini tunapata ladha kidogo ya mada hapa ili tuweze kuona jinsi ufumbuzi wa mfululizo wa milinganyo tofauti hutumiwa katika programu halisi ya ulimwengu. Equation ya Bessel ya utaratibu\(n\) hutolewa na

\[x^2y″+xy′+(x^2−n^2)y=0. \nonumber \]

Equation hii inatokea katika maombi mengi ya kimwili, hasa wale wanaohusisha kuratibu cylindrical, kama vile vibration ya kichwa mviringo ngoma na inapokanzwa muda mfupi au baridi ya silinda. Katika mfano unaofuata, tunapata ufumbuzi wa mfululizo wa nguvu kwa usawa wa Bessel wa utaratibu 0.

Mfano\(\PageIndex{2}\): Power Series Solution to the Bessel Equation

Kupata nguvu mfululizo ufumbuzi Bessel equation ya utaratibu 0 na grafu ufumbuzi.

Suluhisho

Equation ya Bessel ya utaratibu 0 inatolewa na

\[x^2y″+xy′+x^2y=0. \nonumber \]

Tunadhani suluhisho la fomu\(\displaystyle y=\sum_{n=0}^∞ a_nx^n\). Kisha\(\displaystyle y′(x)=\sum_{n=1}^∞ na_nx^{n−1}\) na\(\displaystyle y''(x)=\sum_{n=2}^∞n(n−1)a_nx^{n−2}.\) Kubadilisha hii katika equation tofauti, tunapata

\[\begin{align*} x^2 \sum_{n=2}^∞ n(n−1)a_nx^{n−2}+x \sum_{n=1}^∞ na_nx^{n−1}+x^2 \sum_{n=0}^∞ a_nx^n&=0 & & \text{Substitution.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+\sum_{n=1}^∞ na_nx^n+ \sum_{n=0}^∞ a_nx^{n+2}&=0 & & \text{Bring external factors within sums.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+\sum_{n=1}^∞ na_nx^n+\sum_{n=2}^∞ a_{n−2}x^n &=0 & & \text{Re-index third sum.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+a_1x+\sum_{n=2}^∞ na_nx^n+\sum_{n=2}^∞ a_{n−2}x^n &=0 & & \text{Separate }n=1 \text{ term from second sum.} \\[5pt] a_1x+\sum_{n=2}^∞ [n(n−1)a_n+na_n+a_{n−2}]x^n&=0 & & \text{Collect summation terms.} \\[5pt] a_1x+\sum_{n=2}^∞ [(n^2−n)a_n+na_n+a_{n−2}]x^n &=0 & & \text{Multiply through in first term.} \\[5pt] a_1x+\sum_{n=2}^∞ [n^2a_n+a_{n−2}]x^n &=0. & & \text{Simplify.} \end{align*}\]

Kisha\(a_1=0\), na kwa\(n≥2,\)

\[\begin{align*} n^2a_n+a_{n−2} &= 0 \\[4pt] a_n&=−\dfrac{1}{n^2}a_{n−2}. \end{align*} \nonumber \]

Kwa sababu\(a_1=0\), maneno yote isiyo ya kawaida ni sifuri. Kisha, kwa hata maadili ya\(n,\) tuna

\[\begin{align*}a_2 &=−\dfrac{1}{2^2}a_0 \\[4pt] a_4 &= −\dfrac{1}{4^2}a_2=\dfrac{1}{4^2⋅2^2} a_0. \\[4pt] a_6 &=−\dfrac{1}{6^2}a_4 =−\dfrac{1}{6^2⋅4^2⋅2^2}a_0 \end{align*}\]

Kwa ujumla,

\[a_{2k}=\dfrac{(−1)^k}{(2)^{2k}(k!)^2}a_0. \nonumber \]

Hivyo, tuna

\[y(x)=a_0 \sum_{k=0}^∞ \dfrac{(−1)^k}{(2)^{2k}(k!)^2}x^{2k}. \nonumber \]

Grafu inaonekana hapa chini.

Zoezi\(\PageIndex{2}\)

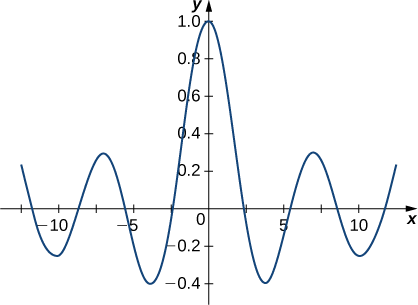
Thibitisha kwamba usemi kupatikana katika Mfano\(\PageIndex{2}\) ni suluhisho la Bessel equation ya utaratibu 0.

Kidokezo

Tofautisha mfululizo wa nguvu kwa muda na uibadilishe katika usawa tofauti.

Dhana muhimu

• Uwakilishi wa mfululizo wa nguvu wa kazi wakati mwingine unaweza kutumika kupata ufumbuzi wa equations tofauti.
• Tofautisha mfululizo wa nguvu kwa muda na mbadala katika equation tofauti ili kupata uhusiano kati ya coefficients mfululizo wa nguvu.