17.3: Matumizi ya Ulinganisho wa Pili wa Tofauti

Last updated
Save as PDF

Page ID: 178815

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Kutatua pili ili tofauti equation anayewakilisha rahisi harmonic mwendo.
Kutatua pili ili tofauti equation anayewakilisha damped rahisi harmonic mwendo.
Kutatua pili ili tofauti equation anayewakilisha kulazimishwa rahisi harmonic mwendo.
Kutatua pili ili tofauti equation anayewakilisha malipo na sasa katika RLC mfululizo mzunguko.

Tuliona katika utangulizi wa sura kwamba equations ya pili ya mstari tofauti hutumiwa kutengeneza hali nyingi katika fizikia na uhandisi. Katika sehemu hii, tunaangalia jinsi hii inavyofanya kazi kwa mifumo ya kitu kilicho na wingi unaohusishwa na spring ya wima na mzunguko wa umeme unao na kupinga, inductor, na capacitor iliyounganishwa katika mfululizo. Mifano kama hizi zinaweza kutumika kwa takriban hali nyingine ngumu zaidi; kwa mfano, vifungo kati ya atomi au molekuli mara nyingi huelekezwa kama chemchemi zinazotetemeka, kama ilivyoelezwa na equations hizi tofauti.

Rahisi Harmonic Motion

Fikiria molekuli imesimamishwa kutoka chemchemi iliyounganishwa na msaada mgumu. (Hii inaitwa mfumo wa spring-molekuli.) Mvuto unaunganisha wingi chini na nguvu ya kurejesha ya chemchemi inaunganisha wingi juu. Kama inavyoonekana katika Kielelezo\(\PageIndex{1}\), wakati majeshi haya mawili ni sawa, wingi inasemekana kuwa katika nafasi ya usawa. Ikiwa umati umehamishwa kutoka kwa usawa, hutembea juu na chini. Tabia hii inaweza kuonyeshwa na equation ya pili ya mgawo wa mgawo wa mara kwa mara.

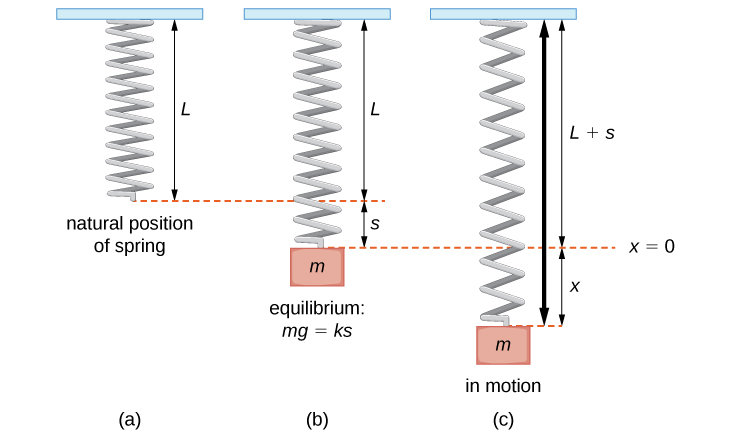
Takwimu hii ina picha tatu za chemchemi. Picha ya kwanza ni chemchemi ya wima katika nafasi yake ya asili na urefu L uliowekwa juu hadi hatua iliyowekwa. Picha ya pili inaonyesha spring wima na molekuli m masharti ya spring, kuenea spring umbali s kutoka L. spring ni katika usawa. Picha ya tatu ni spring wima na molekuli m masharti ambapo spring ni katika mwendo, umbali x kutoka usawa L + s. — Kielelezo\(\PageIndex{1}\): Spring katika nafasi yake ya asili (a), katika usawa na molekuli m masharti (b), na katika mwendo oscillatory (c).

Hebu\(x(t)\) kuashiria uhamisho wa wingi kutoka kwa usawa. Kumbuka kuwa kwa mifumo ya spring ya aina hii, ni desturi kupitisha mkataba ambao chini ni chanya. Kwa hiyo, uhamisho mzuri unaonyesha wingi ni chini ya hatua ya usawa, wakati uhamisho hasi unaonyesha kuwa wingi ni juu ya usawa. Uhamisho kwa kawaida hutolewa kwa miguu katika mfumo wa Kiingereza au mita katika mfumo wa metriki.

Fikiria majeshi yanayofanya juu ya wingi. Nguvu ya mvuto hutolewa na mg.mg. Katika mfumo wa Kiingereza, wingi ni katika slugs na kasi inayotokana na mvuto ni kwa miguu kwa mraba wa pili. Kuongezeka kwa kasi kutokana na mvuto ni mara kwa mara, hivyo katika mfumo wa Kiingereza,\(g=32\, ft/sec^2\). Kumbuka kwamba 1 slug-foot/sec ² ni pound, hivyo mg kujieleza inaweza kuelezwa kwa paundi. Vitengo vya mfumo wa metri ni kilo kwa wingi na m/sec ² kwa kuongeza kasi ya mvuto. Katika mfumo wa metri, tuna\(g=9.8\) m/sec ².

Kwa mujibu wa sheria ya Hooke, nguvu ya kurejesha ya spring inafanana na uhamisho na hufanya kinyume chake kutoka kwa uhamisho, hivyo nguvu ya kurejesha hutolewa na Mara kwa mara\(−k(s+x).\) ya spring hutolewa kwa paundi kwa mguu katika mfumo wa Kiingereza na katika newtons kwa mita katika mfumo wa metri.

Sasa, kwa sheria ya pili ya Newton, jumla ya nguvu kwenye mfumo (mvuto pamoja na nguvu ya kurejesha) ni sawa na kuongeza kasi ya mara nyingi, kwa hiyo tuna

\[\begin{align*}mx″ &=−k(s+x)+mg \\[4pt] &=−ks−kx+mg. \end{align*}\]

Hata hivyo, kwa njia ya sisi defined msawazo wetu msimamo\(mg=ks\), equation tofauti inakuwa

\[mx″+kx=0. \nonumber \]

Ni rahisi kupanga upya equation hii na kuanzisha variable mpya, inayoitwa mzunguko wa angular,\(ω\). Kuruhusu\(ω=\sqrt{k/m}\), tunaweza kuandika equation kama

\[x''+ω^2x=0. \nonumber \]

Equation hii tofauti ina suluhisho la jumla

\[x(t)=c_1 \cos ωt+c_2 \sin ωt, \label{GeneralSol} \]

ambayo inatoa nafasi ya wingi wakati wowote kwa wakati. Mwendo wa wingi huitwa mwendo rahisi wa harmonic. Kipindi cha mwendo huu (wakati inachukua kukamilisha oscillation moja) ni\(T=\dfrac{2π}{ω}\) na mzunguko ni\(f=\dfrac{1}{T}=\dfrac{ω}{2π}\) (Kielelezo\(\PageIndex{2}\)).

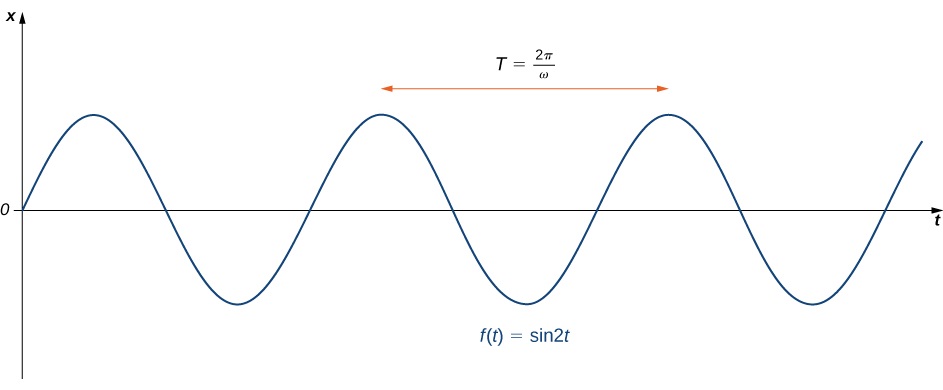
Takwimu hii ni grafu ya f (t) = dhambi 2t. Ni grafu ya mara kwa mara, ya kusonga. Kipindi cha grafu kinawakilishwa na mstari unaoelezea kutoka kilele kimoja hadi kingine. Inaandikwa na kipindi T = 2π/ω. — Kielelezo\(\PageIndex{2}\): Grafu ya makazi ya wima dhidi ya muda kwa ajili ya mwendo rahisi harmonic.

Mfano\(\PageIndex{1}\): Simple Harmonic Motion

Kudhani kitu uzito 2 lb stretches spring 6 katika. Pata usawa wa mwendo ikiwa chemchemi inatolewa kutoka nafasi ya usawa na kasi ya juu ya 16 ft/sec. Ni kipindi gani cha mwendo?

Suluhisho

Sisi kwanza tunahitaji kupata mara kwa mara ya spring. Tuna

\[\begin{align*}mg &=ks\\[4pt] 2 &=k \left(\dfrac{1}{2}\right)\\[4pt] k &=4. \end{align*}\]

Tunajua pia kwamba uzito\(W\) ni sawa na bidhaa ya wingi\(m\) na kuongeza kasi kutokana na mvuto\(g\). Katika vitengo vya Kiingereza, kasi kutokana na mvuto ni 32 ft/sec ².

\[\begin{align*}W &=mg\\[4pt] 2 &=m(32)\\[4pt] m &=\dfrac{1}{16}\end{align*}\]

Hivyo, equation tofauti anayewakilisha mfumo huu ni

\[\dfrac{1}{16}x″+4x=0. \nonumber \]

Kuongezeka kwa njia ya 16, tunapata\(x''+64x=0,\) ambayo inaweza pia kuandikwa kwa fomu Equation\(x''+(8^2)x=0.\) hii ina suluhisho la jumla

\[x(t)=c_1 \cos (8t)+c_2 \sin (8t). \nonumber \]

Masi ilitolewa kutoka nafasi ya usawa, kwa hiyo\(x(0)=0\), na ilikuwa na kasi ya juu ya 16 ft/sec, hivyo\(x′(0)=−16\). Kutumia masharti haya ya awali ya kutatua\(c_1\) na\(c_2\). anatoa

\[x(t)=−2 \sin 8t. \nonumber \]

Kipindi cha mwendo huu ni\(\dfrac{2π}{8}=\dfrac{π}{4}\) sekunde.

Zoezi\(\PageIndex{1}\)

Masi 200-g huweka spring 5 cm. Pata usawa wa mwendo wa wingi ikiwa hutolewa kutoka kwa kupumzika kutoka nafasi 10 cm chini ya msimamo wa usawa. Je! Ni mzunguko gani wa mwendo huu?

Kidokezo: Kwanza kupata mara kwa mara spring.

Jibu: \(x(t)=0.1 \cos (14t)\)(katika mita); frequency ni\(\dfrac{14}{2π}\) Hz.

Kuandika suluhisho la jumla katika fomu\(x(t)=c_1 \cos (ωt)+c_2 \sin(ωt)\) (Equation\ ref {GeneralSol}) ina faida fulani. Ni rahisi kuona kiungo kati ya equation tofauti na suluhisho, na kipindi na mzunguko wa mwendo ni dhahiri. Fomu hii ya kazi inatuambia kidogo sana kuhusu amplitude ya mwendo, hata hivyo. Katika hali fulani, tunaweza kupendelea kuandika suluhisho kwa fomu

\[x(t)=A \sin (ωt+ϕ). \nonumber \]

Ingawa kiungo kwa equation tofauti si kama wazi katika kesi hii, kipindi na mzunguko wa mwendo bado ni dhahiri. Zaidi ya hayo, amplitude ya mwendo,\(A,\) ni dhahiri katika fomu hii ya kazi. Mara kwa mara\(ϕ\) inaitwa mabadiliko ya awamu na ina athari ya kuhama grafu ya kazi kwa kushoto au kulia.

Ili kubadilisha ufumbuzi wa fomu hii, tunataka kupata maadili ya\(A\) na\(ϕ\) vile vile

\[c_1 \cos (ωt)+c_2 \sin (ωt)=A \sin (ωt+ϕ). \nonumber \]

Sisi kwanza kutumia utambulisho trigonometric

\[\sin (α+β)= \sin α \cos β+ \cos α \sin β \nonumber \]

kupata

\[\begin{align*} c_1 \cos (ωt)+c_2 \sin (ωt) &= A( \sin (ωt) \cos ϕ+ \cos (ωt) \sin ϕ) \\[4pt] &= A \sin ϕ( \cos (ωt))+A \cos ϕ( \sin (ωt)). \end{align*}\]

Hivyo,

\[c1=A \sin ϕ \text{ and } c_2=A \cos ϕ. \nonumber \]

Kama sisi mraba wote wa milinganyo haya na kuongeza yao pamoja, sisi kupata

\[\begin{align*}c_1^2+c_2^2 &=A^2 \sin _2 ϕ+A^2 \cos _2 ϕ \\[4pt] &=A^2( \sin ^2 ϕ+ \cos ^2 ϕ) \\[4pt] &=A^2. \end{align*}\]

Hivyo,

\[A=\sqrt{c_1^2+c_2^2}. \nonumber \]

Sasa, kupata\(ϕ\), kurudi kwa equations kwa\(c_1\) na\(c_2\), lakini wakati huu, kugawanya equation kwanza na equation pili kupata

\[\begin{align*} \dfrac{c_1}{c_2} &=\dfrac{A \sin ϕ}{A \cos ϕ} \\[4pt] &= \tan ϕ. \end{align*} \nonumber \]

Kisha,

\[\tan ϕ= \dfrac{c_1}{c_2}. \nonumber \]

Sisi muhtasari huu kutafuta katika theorem ifuatayo.

Solution kwa equation kwa Simple harmonic mwendo

Kazi\(x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)\) inaweza kuandikwa kwa fomu\(x(t)=A \sin (ωt+ϕ)\), wapi\(A=\sqrt{c_1^2+c_2^2}\) na\( \tan ϕ = \dfrac{c_1}{c_2}\).

Kumbuka kwamba wakati wa kutumia formula\( \tan ϕ=\dfrac{c_1}{c_2}\) kupata\(ϕ\), ni lazima kutunza kuhakikisha\(ϕ\) ni katika quadrant haki (Kielelezo\(\PageIndex{3}\)).

Mfano\(\PageIndex{2}\): Expressing the Solution with a Phase Shift

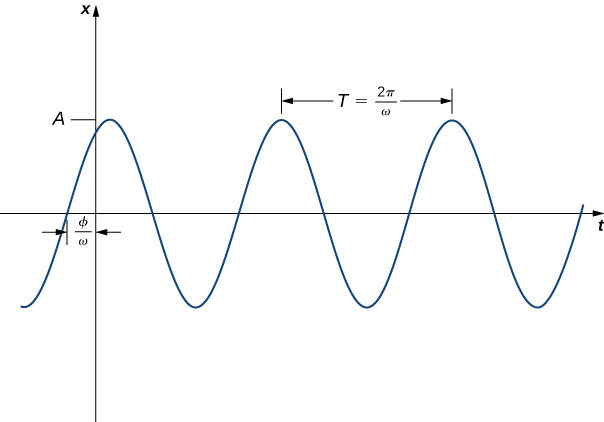
Eleza kazi zifuatazo kwa fomu\(A \sin (ωt+ϕ) \). Mzunguko wa mwendo ni nini? Amplitude?

\(x(t)=2 \cos (3t)+ \sin (3t)\)
\(x(t)=3 \cos (2t)−2 \sin (2t)\)

Suluhisho

Tuna

\[A=\sqrt{c_1^2+c_2^2}=\sqrt{2^2+1^2}=\sqrt{5} \nonumber \]

\[ \tan ϕ = \dfrac{c_1}{c_2}=\dfrac{2}{1}=2. \nonumber \]

Kumbuka kwamba wote wawili\(c_1\) na\(c_2\) ni chanya, hivyo\(ϕ\) ni katika quadrant ya kwanza. Hivyo,

\[ϕ≈1.107 \; \text{rad}, \nonumber \]

hivyo tuna

\[ x(t) = 2 \cos (3t)+ \sin (3t) =5 \sin (3t+1.107). \nonumber \]

Mzunguko ni\(\dfrac{ω}{2π}=\dfrac{3}{2π}≈0.477.\) amplitude ni\(\sqrt{5}\).

Tuna
\[A=\sqrt{c_1^2+c_2^2}=\sqrt{3^2+2^2}=\sqrt{13} \nonumber \]
na
\[ \tan ϕ = \dfrac{c_1}{c_2}= \dfrac{3}{−2}=−\dfrac{3}{2}. \nonumber \]
Kumbuka kwamba\(c_1\) ni chanya lakini\(c_2\) ni hasi, hivyo\(ϕ\) ni katika roboduara ya nne. Hivyo,
\[ϕ≈−0.983 \; \text{rad}, \nonumber \]
hivyo tuna
\[\begin{align*} x(t) &=3 \cos (2t) −2 \sin (2t) \\ &= \sqrt{13} \sin (2t−0.983). \end{align*}\]
Mzunguko ni\(\dfrac{ω}{2π}=\dfrac{2}{2π}≈0.318.\) amplitude ni\(\sqrt{13}\).

Zoezi\(\PageIndex{2}\)

Eleza kazi\(x(t)= \cos (4t) + 4 \sin (4t)\) katika fomu\(A \sin (ωt+ϕ) \). Mzunguko wa mwendo ni nini? Amplitude?

Kidokezo: Tumia mchakato kutoka kwa Mfano\(\PageIndex{2}\).

Jibu: \(x(t)= \sqrt{17} \sin (4t+0.245), \text{frequency} =\dfrac{4}{2π}≈0.637, A=\sqrt{17}\)

Vibrations damped

Kwa mfano ulioelezwa tu, mwendo wa wingi unaendelea kwa muda usiojulikana. Kwa wazi, hii haitokei katika ulimwengu wa kweli. Katika ulimwengu wa kweli, kuna karibu kila mara msuguano katika mfumo, ambayo husababisha oscillations kufa polepole-athari inayoitwa damping. Basi sasa hebu tuangalie jinsi ya kuingiza kwamba nguvu damping katika equation yetu tofauti.

Mifumo ya kimwili ya spring-molekuli karibu daima ina baadhi ya uchafu kutokana na msuguano, upinzani wa hewa, au damper ya kimwili, inayoitwa dashpot (silinda ya nyumatiki; Kielelezo\(\PageIndex{4}\)).

Takwimu hii ni silinda ya nyumatiki. Silinda ni wazi, na pistoni inaweza kuonekana. — Kielelezo\(\PageIndex{4}\): dashpot ni silinda ya nyumatiki ambayo hupunguza mwendo wa mfumo wa oscillating.

Kwa sababu damping kimsingi ni nguvu ya msuguano, tunadhani ni sawa na kasi ya wingi na hufanya kinyume chake. Hivyo nguvu ya uchafu hutolewa na kwa mara\(−bx′\) kwa mara\(b>0\). Tena kutumia sheria ya pili ya Newton, equation tofauti inakuwa

\[mx″+bx′+kx=0. \nonumber \]

Kisha kuhusishwa tabia equation ni

\[mλ^2+bλ+k=0. \nonumber \]

Kutumia formula ya quadratic, tuna

\[λ=\dfrac{−b±\sqrt{b^2−4mk}}{2m}. \nonumber \]

Kama vile katika Equations ya Pili-Order Linear tunazingatia kesi tatu, kulingana na kama equation tabia ina tofauti mizizi halisi, mara kwa mara mizizi halisi, au mizizi tata conjugate.

Uchunguzi wa 1: Vibrations overdamped

Wakati\(b^2>4mk\), tunasema mfumo ni overdamped. Suluhisho la jumla lina fomu

\[x(t)=c_1e^{λ_1t}+c_2e^{λ_2t}, \nonumber \]

ambapo wote wawili\(λ_1\) na\(λ_2\) ni chini ya sifuri. Kwa sababu exponents ni hasi, makazi yao kuoza kwa sifuri baada ya muda, kwa kawaida kabisa haraka. Mifumo ya overdamped haifai (hakuna mabadiliko zaidi ya moja ya mwelekeo), lakini tu kurudi nyuma kuelekea nafasi ya usawa. Kielelezo\(\PageIndex{5}\) inaonyesha nini tabia ya kawaida ya kina damped inaonekana kama.

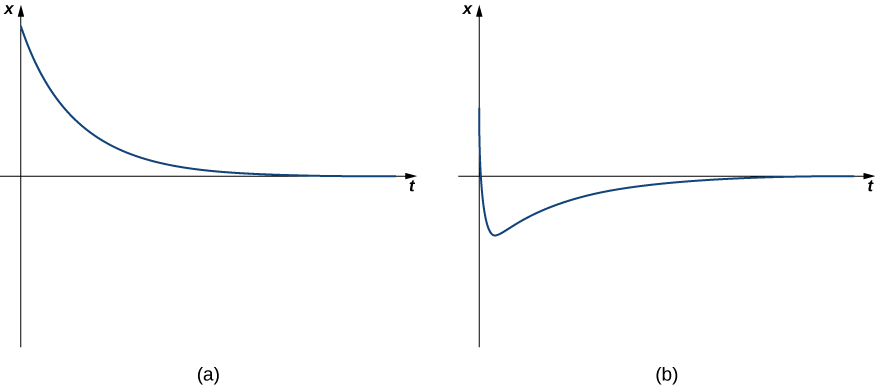
Takwimu hii ina grafu mbili zilizoandikwa (a) na (b). Grafu ya kwanza ni safu ya kupungua na mhimili usio na usawa kama asymptote ya usawa. Grafu ya pili mwanzoni ni kazi ya kupungua lakini inakua chini ya mhimili usio na usawa. Kisha, mhimili usio na usawa pia ni asymptote ya usawa. — Kielelezo\(\PageIndex{5}\): Tabia ya mfumo wa spring-molekuli, bila mabadiliko katika mwelekeo (a) na mabadiliko moja tu katika mwelekeo (b).

Mfano\(\PageIndex{3}\): Overdamped Spring-Mass System

Masi ya 16-lb inaunganishwa na chemchemi ya 10-ft. Wakati umati unapokuja kupumzika katika nafasi ya usawa, hatua ya spring 15 ft 4 in. Mfumo huo umeingizwa katikati ambayo hutoa nguvu ya damping sawa na mara 5252 kasi ya papo hapo ya wingi. Pata usawa wa mwendo ikiwa wingi unasukumwa juu kutoka nafasi ya usawa na kasi ya juu ya 5 ft/sec. Je! Ni nafasi gani ya wingi baada ya sekunde 10? Kasi yake?

Suluhisho

Masi huweka spring 5 ft 4 in., au\(\dfrac{16}{3}\) ft. Hivyo,\(16=\left(\dfrac{16}{3}\right)k,\) hivyo\(k=3.\) sisi pia\(m=\dfrac{16}{32}=\dfrac{1}{2}\), hivyo equation tofauti ni

\[\dfrac{5}{2}x′+3x=0. \nonumber \]

Kuongezeka kwa njia ya 2 inatoa\(x″+5x′+6x=0\), ambayo ina suluhisho la jumla

\[x(t)=c_1e^{−2t}+c_2e^{−3t}. \nonumber \]

Kutumia hali ya awali,\(x(0)=0\) na\(x′(0)=−5\), tunapata

\[x(t)=−5e^{−2t}+5e^{−3t}. \nonumber \]

Baada ya sekunde 10 molekuli iko katika nafasi

\[x(10)=−5e^{−20}+5e^{−30}≈−1.0305×10^{−8}≈0, \nonumber \]

hivyo ni, kwa ufanisi, katika nafasi ya usawa. Sisi\(x′(t)=10e^{−2t}−15e^{−3t}\), hivyo baada ya sekunde 10 molekuli ni kusonga kwa kasi ya

\[x′(10)=10e^{−20}−15e^{−30}≈2.061×10^{−8}≈0. \nonumber \]

Baada ya sekunde 10 tu, wingi hauwezi kusonga.

Zoezi\(\PageIndex{3}\)

Masi ya kilo 2 imeunganishwa na chemchemi na mara kwa mara ya spring 24 N/m. mfumo ni kisha kuzama katika kati, kutoa damping nguvu sawa na mara 16 kasi instantaneous ya wingi. Pata equation ya mwendo ikiwa inatolewa kutoka kupumzika kwenye hatua 40 cm chini ya usawa.

Kidokezo: Fuata mchakato kutoka kwa mfano uliopita.

Jibu: \(x(t)=0.6e^{−2t}−0.2e^{−6t}\)

Uchunguzi wa 2: Vibrations vya kina

Wakati\(b^2=4mk\), tunasema mfumo ni kina damped. Suluhisho la jumla lina fomu

\[x(t)=c_1e^{λ_1t}+c_2te^{λ_1t}, \nonumber \]

ambapo\(λ_1\) ni chini ya sifuri. Mwendo wa mfumo wa kina damped ni sawa na ile ya mfumo overdamped. Haina oscillate. Hata hivyo, kwa mfumo wa kina damped, ikiwa damping imepunguzwa hata kidogo, matokeo ya tabia ya oscillatory. Kwa mtazamo wa vitendo, mifumo ya kimwili ni karibu daima ama overdamped au underdamped (kesi 3, ambayo tunaona ijayo). Haiwezekani kufuta sifa za mfumo wa kimwili ili\(b^2\) na\(4mk\) ni sawa sawa. Kielelezo\(\PageIndex{6}\) inaonyesha nini tabia ya kawaida ya kina damped inaonekana kama.

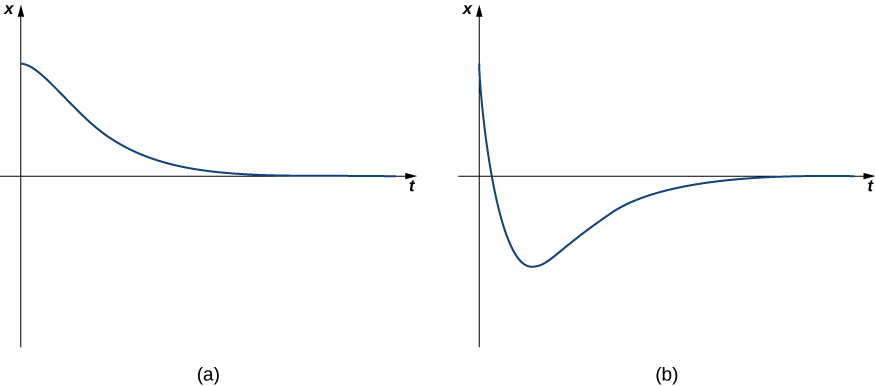
Takwimu hii ina grafu mbili zilizoandikwa (a) na (b). Grafu ya kwanza iko katika quadrant ya kwanza na ni safu ya kupungua na mhimili usio na usawa kama asymptote ya usawa. Grafu ya pili mwanzoni ni kazi ya kupungua lakini inakua chini ya mhimili usio na usawa. Kisha, mhimili usio na usawa pia ni asymptote ya usawa. — Kielelezo\(\PageIndex{6}\): Tabia ya mfumo wa spring-molekuli wa kina. Mfumo uliowekwa katika sehemu (a) una damping zaidi kuliko mfumo uliowekwa katika sehemu (b).

Mfano\(\PageIndex{4}\): Critically Damped Spring-Mass System

Masi ya kilo 1 huweka spring 20 cm. Mfumo huo umeunganishwa na dashpot ambayo hutoa nguvu ya uchafu sawa na mara 14 kasi ya haraka ya wingi. Pata usawa wa mwendo ikiwa wingi hutolewa kutoka kwa usawa na kasi ya juu ya 3 m/sec.

Suluhisho

Tuna\(mg=1(9.8)=0.2k\), hivyo\(k=49.\) basi, equation tofauti ni

\[x″+14x′+49x=0, \nonumber \]

ambayo ina suluhisho la jumla

\[x(t)=c_1e^{−7t}+c_2te^{−7t}. \nonumber \]

Kutumia hali ya awali\(x(0)=0\) na\(x′(0)=−3\) inatoa

\[x(t)=−3te^{−7t}. \nonumber \]

Zoezi\(\PageIndex{4}\)

Uzito wa 1-lb unenea chemchemi 6 ndani., na mfumo unaunganishwa na dashpot ambayo hutoa nguvu ya uchafu sawa na kasi ya nusu ya papo hapo ya wingi. Pata usawa wa mwendo ikiwa wingi unatolewa kutoka kwa kupumzika kwa hatua ya 6 katika. chini ya usawa.

Kidokezo: Kwanza kupata mara kwa mara spring.

Jibu: \(x(t)=\dfrac{1}{2}e^{−8t}+4te^{−8t} \)

Uchunguzi wa 3: Vibrations zisizopigwa

Wakati\(b^2<4mk\), tunasema mfumo ni underdamped. Suluhisho la jumla lina fomu

\[x(t)=e^{αt}(c_1 \cos (βt) + c_2 \sin (βt)), \nonumber \]

ambapo\(α\) ni chini ya sifuri. Mifumo ya underdamped haifai kwa sababu ya maneno ya sine na cosine katika suluhisho. Hata hivyo, neno la ufafanuzi linatawala hatimaye, hivyo amplitude ya oscillations hupungua kwa muda. Kielelezo\(\PageIndex{7}\) inaonyesha nini tabia ya kawaida underdamped inaonekana kama.

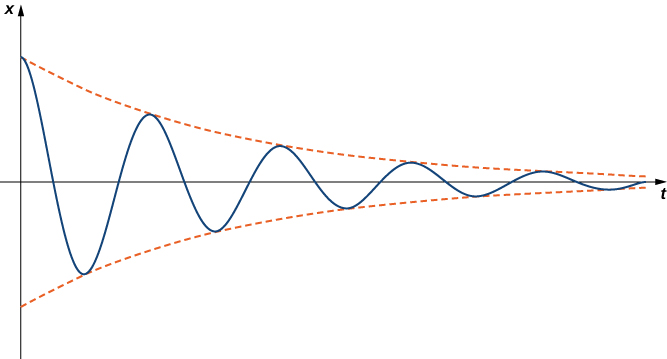
Takwimu hii ni grafu ya oscillating ambapo amplitude inapungua. Kuna curves nyekundu zilizopigwa kwenye kilele cha amplitudes kuonyesha mfano wa amplitude iliyopungua. Kama inavyoongezeka, mhimili usio na usawa unakuwa dalili ya usawa. — Kielelezo\(\PageIndex{7}\): Tabia ya mfumo wa spring-molekuli underdamped.

Kumbuka kuwa kwa mifumo yote ya damped,\( \lim \limits_{t \to \infty} x(t)=0\). Mfumo daima unakaribia nafasi ya usawa kwa muda.

Mfano\(\PageIndex{5}\): Underdamped Spring-Mass System

Uzito wa 16-lb huweka spring 3.2 ft. Fikiria nguvu ya uchafu kwenye mfumo ni sawa na kasi ya papo hapo ya wingi. Kupata equation ya mwendo kama wingi ni huru kutoka kupumzika katika hatua 9 katika. chini ya usawa.

Suluhisho

Tuna\(k=\dfrac{16}{3.2}=5\) na\(m=\dfrac{16}{32}=\dfrac{1}{2},\) hivyo equation tofauti ni

\[\dfrac{1}{2} x″+x′+5x=0, \; \text{or} \; x″+2x′+10x=0. \nonumber \]

Equation hii ina suluhisho la jumla

\[x(t)=e^{−t} ( c_1 \cos (3t)+c_2 \sin (3t) ) . \nonumber \]

Kutumia hali ya awali,\(x(0)=\dfrac{3}{4}\) na\(x′(0)=0,\) sisi kupata

\[x(t)=e^{−t} \bigg( \dfrac{3}{4} \cos (3t)+ \dfrac{1}{4} \sin (3t) \bigg) . \nonumber \]

Zoezi\(\PageIndex{5}\)

Masi ya kilo 1 huweka spring 49 cm. Mfumo huo umeingizwa katikati ambayo hutoa nguvu ya uchafu sawa na mara nne kasi ya papo hapo ya wingi. Pata usawa wa mwendo ikiwa wingi unatolewa kutoka kupumzika kwenye hatua ya 24 cm juu ya usawa.

Kidokezo: Kwanza kupata mara kwa mara spring.

Jibu: \(x(t)=−0.24e^{−2t} \cos (4t)−0.12e^{−2t} \sin (4t) \)

Mfano\(\PageIndex{6}\): Chapter Opener: Modeling a Motorcycle Suspension System

Kwa wanunuzi wa motocross, mifumo ya kusimamishwa kwenye pikipiki zao ni muhimu sana. Kozi za mbali-barabara ambazo hupanda mara nyingi hujumuisha kuruka, na kupoteza udhibiti wa pikipiki wakati wa ardhi inaweza kuwapa gharama mbio.

Picha hii ni mshtuko wa mshtuko kwenye pikipiki. — Kielelezo\(\PageIndex{8}\): (mikopo: mabadiliko ya kazi na NSEika, Flickr)

Mfumo huu wa kusimamishwa unaweza kuonyeshwa kama mfumo wa molekuli wa spring. Tunafafanua sura yetu ya kumbukumbu kwa heshima na sura ya pikipiki. Fikiria mwisho wa mshtuko wa mshtuko unaohusishwa na sura ya pikipiki ni fasta. Kisha, “molekuli” katika mfumo wetu wa spring ni gurudumu la pikipiki. Tunapima nafasi ya gurudumu kwa heshima na sura ya pikipiki. Hii inaweza kuonekana kinyume, kwani, katika hali nyingi, ni kweli sura ya pikipiki inayohamia, lakini sura hii ya kumbukumbu inalinda maendeleo ya equation tofauti ambayo ilifanyika mapema. Kama ilivyo na maendeleo ya awali, tunafafanua mwelekeo wa kushuka kuwa chanya.

Wakati pikipiki inapoinuliwa na sura yake, gurudumu hutegemea kwa uhuru na chemchemi haifai. Hii ni nafasi ya asili ya spring. Wakati pikipiki imewekwa chini na wapanda farasi hupanda pikipiki, compresses spring na mfumo ni katika nafasi ya usawa (Kielelezo\(\PageIndex{9}\)).

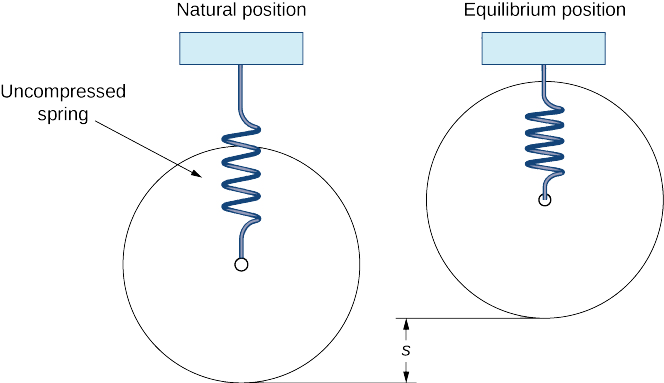
Takwimu hii ina chemchemi mbili zilizounganishwa hapo juu kwenye hatua iliyowekwa. Spring ya kwanza inaitwa, “Msimamo wa Asili,” na ina spring isiyojumuishwa kunyongwa kwa wima. Spring ya pili inaitwa, “Msimamo wa Msawazo,” na ina spring iliyosimamiwa kunyongwa kwa wima. Tofauti ya wima kati ya chemchemi mbili ni kinachoitwa, “s.” — Kielelezo\(\PageIndex{9}\): Tunaweza kutumia mfumo wa molekuli ya spring ili kuiga kusimamishwa kwa pikipiki.

Mfumo huu unaweza kutajwa kwa kutumia equation sawa tofauti tuliyotumia kabla:

\[mx″+bx′+kx=0. \nonumber \]

Motocross pikipiki ina uzito 204 lb, na sisi kudhani mpanda uzito wa 180 lb Wakati mpanda milimani pikipiki, kusimamishwa compresses 4 in., kisha anakuja kupumzika katika usawa. Mfumo wa kusimamishwa hutoa damping sawa na mara 240 kasi ya wima instantaneous ya pikipiki (na wapanda farasi).

Weka equation tofauti kwamba mifano ya tabia ya mfumo wa kusimamishwa pikipiki.
Sisi ni nia ya nini kinatokea wakati pikipiki ardhi baada ya kuchukua kuruka. Hebu muda\[t=0 \nonumber \] unaashiria wakati ambapo pikipiki kwanza inawasiliana na ardhi. Kama pikipiki hits ardhi kwa kasi ya 10 ft/sec chini, kupata equation ya mwendo wa pikipiki baada ya kuruka.
Grafu equation ya mwendo juu ya pili ya kwanza baada ya pikipiki hits ardhi.

Suluhisho

Sisi defined msawazo kuwa mahali ambapo\(mg=ks\), hivyo tuna
\[\begin{align*} mg &=ks \\ 384 &=k\left(\dfrac{1}{3}\right)\\ k &=1152. \end{align*}\]

Pia tuna

\[\begin{align*} W &=mg \\ 384 &=m(32) \\ m &=12. \end{align*}\]

Kwa hiyo, tofauti equation kwamba mifano ya tabia ya kusimamishwa pikipiki ni

\[12x″+240x′+1152x=0. \nonumber \]

Kugawanya kupitia kwa 12, tunapata

\[x''+20x′+96x=0. \nonumber \]
Equation tofauti kupatikana katika sehemu ya a. ina suluhisho la jumla
\[x(t)=c_1e^{−8t}+c_2e^{−12t}. \nonumber \]

Sasa, ili kuamua hali yetu ya awali, tunazingatia nafasi na kasi ya gurudumu la pikipiki wakati gurudumu linawasiliana kwanza na ardhi. Tangu pikipiki ilikuwa hewani kabla ya kuwasiliana na ardhi, gurudumu lilikuwa likinyongwa kwa uhuru na chemchemi haikuwa imefungwa. Kwa hiyo gurudumu ni 4 katika. \(\left(\dfrac{1}{3}\text{ ft}\right)\)chini ya msimamo wa usawa (kuhusiana na sura ya pikipiki), na tuna\(x(0)=\dfrac{1}{3}.\) Kulingana na taarifa ya tatizo, pikipiki ina kasi ya 10 ft/sec kushuka wakati pikipiki mawasiliano ya ardhi, hivyo\(x′(0)=10.\) Kutumia hali hizi za awali, tunapata\(c_1=\dfrac{7}{2}\) na \(c_2=−\left(\dfrac{19}{6}\right)\), hivyo equation ya mwendo ni

\[x(t)=\dfrac{7}{2}e^{−8t}−\dfrac{19}{6}e^{−12t}. \nonumber \]
Grafu inavyoonyeshwa kwenye Kielelezo\(\PageIndex{10}\).

Takwimu hii ni grafu ya kazi f (x) = 7/2e ^-8t -19/6e ^-12t. Mhimili wa wima umewekwa kwa vipimo vya 0.05, na mhimili usio na usawa umeandikwa, “t.” Ni kuongezwa kwa nyongeza ya kumi. Grafu inazunguka mhimili usio na usawa unaoongezeka, hufikia kiwango cha juu, kisha hupungua. Mhimili usio na usawa ni asymptote ya usawa. — Kielelezo\(\PageIndex{10}\): Grafu ya equation ya mwendo juu ya muda wa pili.

KUTUA GARI

NASA inapanga utume wa Mars. Ili kuokoa pesa, wahandisi wameamua kukabiliana na moja ya magari ya kutua mwezi kwa ujumbe mpya. Hata hivyo, wana wasiwasi juu ya jinsi nguvu tofauti za mvuto zitaathiri mfumo wa kusimamishwa ambao hutia hila wakati inagusa chini. Kuongezeka kwa kasi kutokana na mvuto kwenye mwezi ni 1.6 m/sec ², ambapo Mars ni 3.7 m/sec ².

Mfumo wa kusimamishwa kwenye hila unaweza kuonyeshwa kama mfumo wa molekuli wa spring. Katika kesi hiyo, chemchemi iko chini ya mchanga wa mwezi, hivyo chemchemi imesisitizwa kidogo katika usawa, kama inavyoonekana kwenye Mchoro\(\PageIndex{11}\).

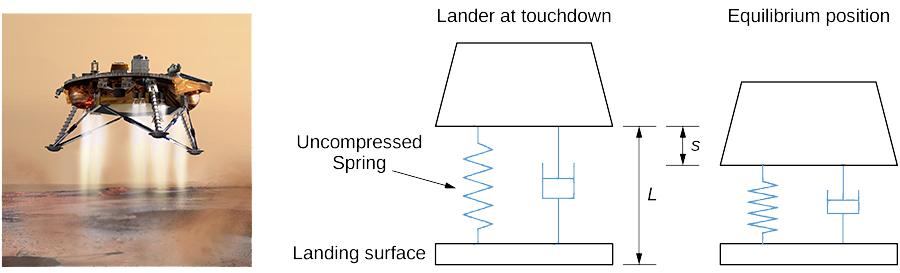
Takwimu hii ina picha tatu. Ya kwanza ni picha ya kutua kwa Mars Lander juu ya uso. Picha ya pili ni mchoro wa Lander ya Mars wakati wa kugusa, na chemchemi isiyojumuishwa na urefu L kati ya Lander na uso wa kutua. Picha ya tatu ni mchoro wa Lander katika nafasi ya usawa baada ya Lander imetua. Spring imesisitizwa umbali wa s. — Kielelezo\(\PageIndex{11}\): Kusimamishwa kwa hila ya kutua kunaweza kuwakilishwa kama mfumo wa molekuli wa spring. (mikopo “Lander”: NASA)

Sisi kurejesha mkataba kwamba chini ni chanya. Licha ya mwelekeo mpya, uchunguzi wa vikosi vinavyoathiri Lander unaonyesha kwamba equation sawa tofauti inaweza kutumika kutengeneza nafasi ya hila ya kutua kuhusiana na usawa:

\[mx''+bx′+kx=0, \nonumber \]

wapi\(m\) wingi wa Lander,\(b\) ni mgawo wa damping, na\(k\) ni mara kwa mara ya spring.

Lander ina wingi wa kilo 15,000 na chemchemi ni m 2 kwa muda mrefu wakati uncompressed. Lander imeundwa ili kuimarisha spring 0.5 m kufikia nafasi ya usawa chini ya mvuto wa mwezi. Dashpot hutoa nguvu ya uchafu sawa na mara 48,000 kasi ya papo hapo ya lander. Weka equation tofauti kwamba mifano ya mwendo wa Lander wakati hila ardhi juu ya mwezi.
Hebu wakati\(t=0\) unaashiria papo hapo Lander inagusa chini. Kiwango cha ukoo wa Lander kinaweza kudhibitiwa na wafanyakazi, hivyo kwamba ni kushuka kwa kiwango cha 2 m/sec wakati inagusa chini. Find equation ya mwendo wa Lander juu ya mwezi.
Kama Lander ni kusafiri kwa kasi mno wakati kugusa chini, inaweza kikamilifu compress spring na “chini nje.” Bottoming nje inaweza kuharibu kutua hila na lazima kuepukwa kwa gharama zote. Grafu equation ya mwendo kupatikana katika sehemu ya 2. Ikiwa chemchemi ni urefu wa 0.5 m wakati imesisitizwa kikamilifu, je, lander itakuwa katika hatari ya kuacha nje?
Kutokana na wahandisi wa NASA hawana marekebisho kwa chemchemi au damper, ni mbali gani Lander inakabiliwa na spring kufikia msimamo wa usawa chini ya mvuto wa Martian?
Kama wafanyakazi Lander anatumia taratibu sawa juu ya Mars kama juu ya mwezi, na anaendelea kiwango cha asili ya 2 m/sec, itakuwa Lander chini nje wakati ardhi juu ya Mars?
Je, ni marekebisho gani, ikiwa ni lazima wahandisi wa NASA wafanye kutumia salama kwenye Mars?

Vibrations kulaz

Kesi ya mwisho tunayofikiria ni wakati nguvu ya nje inachukua mfumo. Katika kesi ya mfumo wa kusimamishwa kwa pikipiki, kwa mfano, matuta katika barabara hufanya kama nguvu ya nje inayofanya mfumo. Mfano mwingine ni spring kunyongwa kutoka msaada; kama msaada ni kuweka katika mwendo, mwendo huo itakuwa kuchukuliwa nguvu ya nje juu ya mfumo. Tunaiga mifumo hii ya kulazimishwa na equation isiyo ya kawaida ya kutofautiana

\[mx″+bx′+kx=f(t), \nonumber \]

ambapo nguvu ya nje inawakilishwa na\(f(t)\) neno. Kama tulivyoona katika Equations Linear Nonhomogenous, equations tofauti kama hii ina ufumbuzi wa fomu

\[x(t)=c_1x_1(t)+c_2x_2(t)+x_p(t), \nonumber \]

\(c_1x_1(t)+c_2x_2(t)\)wapi suluhisho la jumla la equation ya ziada na\(x_p(t)\) ni suluhisho fulani kwa equation isiyo ya kawaida. Kama mfumo ni damped,\(\lim \limits_{t \to \infty} c_1x_1(t)+c_2x_2(t)=0.\) Tangu maneno haya hayaathiri tabia ya muda mrefu ya mfumo, tunaita sehemu hii ya ufumbuzi ufumbuzi wa muda mfupi. Tabia ya muda mrefu ya mfumo imedhamiriwa na\(x_p(t)\), kwa hiyo tunaita sehemu hii ya suluhisho ufumbuzi wa hali ya kutosha.

Mfano\(\PageIndex{7}\): Forced Vibrations

Masi ya slug 1 huweka spring 2 ft na huja kupumzika kwa usawa. Mfumo huo umeunganishwa na dashpot ambayo hutoa nguvu ya damping sawa na mara nane kasi ya papo hapo ya wingi. Kupata equation ya mwendo kama nguvu ya nje sawa na\(f(t)=8 \sin (4t)\) inatumika kwa mfumo kuanzia wakati\(t=0\). Suluhisho la muda mfupi ni nini? Suluhisho la hali ya kutosha ni nini?

Suluhisho

Tuna\(mg=1(32)=2k,\) hivyo\(k=16\) na equation tofauti ni

\[x″+8x′+16x=8 \sin (4t). \nonumber \]

Suluhisho la jumla la equation ya ziada ni

\[c_1e^{−4t}+c_2te^{−4t}. \nonumber \]

Kutokana na suluhisho fulani la fomu\(x_p(t)=A \cos (4t)+ B \sin (4t)\) na kutumia njia ya coefficients isiyojulikana, tunaona\(x_p (t)=−\dfrac{1}{4} \cos (4t)\), hivyo

\[x(t)=c_1e^{−4t}+c_2te^{−4t}−\dfrac{1}{4} \cos (4t). \nonumber \]

Katika\(t=0,\) wingi ni kupumzika katika nafasi ya usawa, hivyo\(x(0)=x′(0)=0.\) Kutumia masharti haya ya awali ya kutatua\(c_1\) na\(c_2,\) sisi kupata

\[x(t)=\dfrac{1}{4}e^{−4t}+te^{−4t}−\dfrac{1}{4} \cos (4t). \nonumber \]

Suluhisho la muda mfupi ni\(\dfrac{1}{4}e^{−4t}+te^{−4t}\). Suluhisho la hali ya kutosha ni\(−\dfrac{1}{4} \cos (4t).\)

Zoezi\(\PageIndex{6}\)

Masi ya kilo 2 inaunganishwa na chemchemi na mara kwa mara 32 N/m na inakuja kupumzika katika nafasi ya usawa. Kuanzia wakati\(t=0\), nguvu ya nje sawa\(f(t)=68e^{−2}t \cos (4t) \) na inatumika kwenye mfumo. Find equation ya mwendo kama hakuna damping. Suluhisho la muda mfupi ni nini? Suluhisho la hali ya kutosha ni nini?

Kidokezo: Pata suluhisho maalum kabla ya kutumia hali ya awali.

Jibu

\(x(t)=−\dfrac{1}{2} \cos (4t)+ \dfrac{9}{4} \sin (4t)+ \dfrac{1}{2} e^{−2t} \cos (4t)−2e^{−2t} \sin (4t)\)

\(\text{Transient solution:} \dfrac{1}{2}e^{−2t} \cos (4t)−2e^{−2t} \sin (4t)\)

\(\text{Steady-state solution:} −\dfrac{1}{2} \cos (4t)+ \dfrac{9}{4} \sin (4t) \)

resONANCE

Fikiria mfumo usio na uharibifu unaoonyesha mwendo rahisi wa harmonic. Katika ulimwengu wa kweli, hatuwezi kuwa na mfumo usio na uharibifu; -baadhi ya uchafu hutokea kila wakati. Kwa madhumuni ya kinadharia, hata hivyo, tunaweza kufikiria mfumo wa molekuli wa spring ulio na chumba cha utupu. Kwa upinzani wowote wa hewa, wingi utaendelea kusonga juu na chini kwa muda usiojulikana.

Mzunguko wa mwendo unaosababishwa, uliotolewa na\(f=\dfrac{1}{T}=\dfrac{ω}{2π}\), huitwa mzunguko wa asili wa mfumo. Ikiwa nguvu ya nje inayofanya mfumo ina mzunguko karibu na mzunguko wa asili wa mfumo, jambo linaloitwa matokeo ya resonance. Nguvu ya nje inaimarisha na kuimarisha mwendo wa asili wa mfumo.

Fikiria equation tofauti\(x″+x=0.\) Pata suluhisho la jumla. Je, ni mzunguko wa asili wa mfumo?
Sasa tuseme mfumo huu unakabiliwa na nguvu ya nje iliyotolewa na\(f(t)=5 \cos t.\) Tatua tatizo la thamani ya awali\(x″+x=5 \cos t\),\(x(0)=0\),\(x′(0)=1\).
Graph suluhisho. Ni nini kinachotokea kwa tabia ya mfumo kwa muda?
Katika ulimwengu wa kweli, daima kuna baadhi ya uchafu. Hata hivyo, kama nguvu ya uchafu ni dhaifu, na nguvu ya nje ni ya kutosha, mifumo halisi ya ulimwengu bado inaweza kuonyesha resonance. Mojawapo ya mifano maarufu zaidi ya resonance ni kuanguka kwa Daraja la Tacoma Narrows mnamo Novemba 7, 1940. Daraja hilo lilikuwa limeonyesha tabia ya ajabu tangu kujengwa. Barabara ilikuwa na “bounce” ya ajabu. Siku hiyo ilipoanguka, upepo mkali ulisababisha barabara kupotosha na kupasuka kwa ukali. Daraja hilo halikuweza kuhimili vikosi hivi na hatimaye ikaanguka. Wataalam wanaamini kuwa upepo wa upepo ulijitokeza nguvu kwenye daraja ambalo lilikuwa karibu sana na mzunguko wake wa asili, na resonance iliyosababisha hatimaye ilitetemeka daraja mbali.
Tovuti hii ina taarifa zaidi kuhusu kuanguka kwa Daraja la Tacoma Narrows.

Wakati mfupi daraja la Tacoma Narrows lilisimama, likawa kivutio cha utalii kabisa. Watu kadhaa walikuwa kwenye tovuti siku daraja liliporomoka, na mmoja wao hawakupata kuanguka kwenye filamu.

Tazama video ili uone kuanguka kwa Daraja la Tacoma Narrows “Gallopin' Gertie”. https://www.youtube.com/watch?v=j-zczJXSxnw

Mfano mwingine halisi ya ulimwengu wa resonance ni mwimbaji shattering wineglass kioo wakati yeye anaimba tu kumbuka haki. Wakati mtu anapiga kioo cha divai ya kioo au hupunguza kidole na anaendesha karibu na mdomo, sauti inaweza kusikilizwa. Kumbuka kwamba ni iliyoundwa na vibrating mvinyo katika mzunguko wake wa asili. Ikiwa mwimbaji basi anaimba alama hiyo hiyo kwa kiasi kikubwa cha kutosha, kioo hupasuka kama matokeo ya resonance.
Kipindi cha televisheni cha Mythbusters kilirushwa hewani kipindi cha tukio hili. Tembelea tovuti hii ili ujifunze zaidi kuhusu hilo. Adam Savage pia alielezea uzoefu. Tazama video hii kwa akaunti yake.

Mzunguko wa mfululizo wa RLC

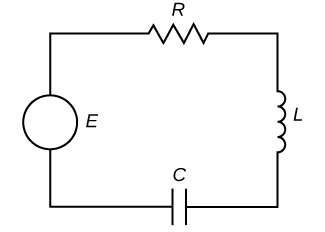
Fikiria mzunguko wa umeme ulio na kupinga, inductor, na capacitor, kama inavyoonekana kwenye Mchoro\(\PageIndex{12}\). Mzunguko huo unaitwa mzunguko wa mfululizo wa RLC. Mzunguko wa RLC hutumiwa katika mifumo mingi ya umeme, hasa kama Cables katika redio za AM/FM. Knob tuning inatofautiana capacitance ya capacitor, ambayo kwa upande wake tunes redio. Mzunguko huo unaweza kuonyeshwa na utaratibu wa pili, usawa wa mgawo wa mgawo wa mara kwa mara.

Hebu\(I(t)\) kuashiria sasa katika mzunguko wa RLC na\(q(t)\) ueleze malipo kwenye capacitor. Zaidi ya hayo, hebu\(L\) kuashiria inductance katika henrys (H),\(R\) kuashiria upinzani katika ohms\((Ω)\), na\(C\) kuashiria capacitance katika farads (F). Mwisho, hebu\(E(t)\) ueleze uwezo wa umeme katika volts (V).

Utawala wa voltage wa Kirchhoff unasema kwamba jumla ya matone ya voltage karibu na kitanzi chochote kilichofungwa lazima iwe sifuri. Kwa hiyo, tunahitaji kuzingatia matone ya voltage kwenye inductor (iliyoashiria\(E_L\)), kupinga (iliyoashiria\(E_R\)), na capacitor (iliyoashiria\(E_C\)). Kwa sababu mzunguko RLC inavyoonekana katika Kielelezo\(\PageIndex{12}\) ni pamoja na chanzo voltage\(E(t)\),, ambayo inaongeza voltage kwa mzunguko, tuna\(E_L+E_R+E_C=E(t)\).

Tunawasilisha formula hapa chini bila maendeleo zaidi na wale wenu wanaopenda kupata fomu hizi wanaweza kupitia viungo. Kwa kutumia sheria ya Faraday na sheria ya Lenz, kushuka kwa voltage katika inductor inaweza kuonyeshwa kuwa sawa na kiwango cha instantaneous cha mabadiliko ya sasa, na uwiano wa mara kwa mara\(L.\) Hivyo,

\[E_L=L\dfrac{dI}{dt}. \nonumber \]

Kisha, kwa mujibu wa sheria ya Ohm, kushuka kwa voltage katika kupinga ni sawia na sasa inayopita kupitia kupinga, na uwiano wa mara kwa mara\(R.\) Kwa hiyo,

\[E_R=RI. \nonumber \]

Mwisho, kushuka kwa voltage katika capacitor ni sawia na malipo,\(q,\) juu ya capacitor, na uwiano mara kwa mara\(1/C\). Hivyo,

\[E_C=\dfrac{1}{C}q. \nonumber \]

Kuongeza maneno haya pamoja, tunapata

\[L\dfrac{dI}{dt}+RI+\dfrac{1}{C}q=E(t). \nonumber \]

Akibainisha kuwa\(I=(dq)/(dt)\), hii inakuwa

\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t). \nonumber \]

Kihisabati, mfumo huu ni sawa na mifumo ya spring molekuli tumekuwa kuchunguza katika sehemu hii.

Takwimu hii ni mchoro wa mzunguko. Ina kuvunjwa mistari chini kinachoitwa C. upande wa kushoto kuna mduara wazi kinachoitwa E. juu ina mistari mshazari kinachoitwa R. upande wa kulia ina matuta kidogo kinachoitwa L. — Kielelezo\(\PageIndex{12}\): Mzunguko wa mfululizo wa *RLC* unaweza kuelekezwa na equation sawa tofauti kama mfumo wa moleku-spring.

mfululizo Circuit

Kupata malipo juu ya capacitor katika mzunguko RLC mfululizo ambapo\(L=5/3\) H,\(C=1/30\) F\(R=10Ω\), na\(E(t)=300\) V. kudhani malipo ya awali juu ya capacitor ni 0 C na sasa ya awali ni 9 A. nini kinatokea kwa malipo ya capacitor baada ya muda?

Suluhisho

Tuna

\[\begin{align*} L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q &=E(t) \\[4pt] \dfrac{5}{3} \dfrac{d^2q}{dt^2}+10\dfrac{dq}{dt}+30q &=300 \\[4pt] \dfrac{d^2q}{dt^2}+6\dfrac{dq}{dt}+18q &=180. \end{align*}\]

Suluhisho la jumla la equation ya ziada ni

\[e^{−3t}(c_1 \cos (3t)+c_2 \sin (3t)). \nonumber \]

Fikiria suluhisho fulani la fomu\(q_p=A\), wapi\(A\) mara kwa mara. Kutumia njia ya coefficients isiyojulikana, tunapata\(A=10\). Hivyo,

\[q(t)=e^{−3t}(c_1 \cos (3t)+c_2 \sin (3t))+10. \nonumber \]

Kutumia hali ya awali\(q(0)=0\) na\(i(0)=((dq)/(dt))(0)=9,\) tunapata\(c_1=−10\) na\(c_2=−7.\) Hivyo malipo kwenye capacitor ni

\[q(t)=−10e^{−3t} \cos (3t)−7e^{−3t} \sin (3t)+10. \nonumber \]

Kuangalia kwa karibu katika kazi hii, tunaona kwanza maneno mawili kuoza baada ya muda (kama matokeo ya exponent hasi katika kazi kielelezo). Kwa hiyo, capacitor hatimaye inakaribia malipo ya hali ya kutosha ya 10 C.

Zoezi\(\PageIndex{7}\)

Pata malipo kwenye capacitor katika mzunguko wa mfululizo wa RLC ambapo\(L=1/5\) H,\(R=2/5Ω,\)\(C=1/2\) F, na\(E(t)=50\) V. kudhani malipo ya awali kwenye capacitor ni 0 C na sasa ya awali ni 4 A.

Kidokezo: Kumbuka,\(E_L=L((dI)/(dt)).\)

Jibu: \[q(t)=−25e^{−t} \cos (3t)−7e^{−t} \sin (3t)+25 \nonumber \]

Dhana muhimu

Ulinganisho wa pili wa mgawo wa mgawo wa mara kwa mara unaweza kutumika kutengeneza mifumo ya spring-molekuli.
Uchunguzi wa majeshi kwenye mfumo wa molekuli wa spring husababisha usawa tofauti wa fomu\[mx″+bx′+kx=f(t), \nonumber \] ambapo mm inawakilisha wingi, bb ni mgawo wa nguvu ya damping,\(k\) ni mara kwa mara ya spring, na\(f(t)\) inawakilisha nguvu yoyote ya nje ya mfumo.
Kama\(b=0\), hakuna nguvu damping kaimu juu ya mfumo, na matokeo rahisi harmonic mwendo.
Ikiwa\(b≠0\), tabia ya mfumo inategemea ikiwa\(b^2−4mk>0, b^2−4mk=0,\) au\(b^2−4mk<0.\)
- Ikiwa\(b^2−4mk>0,\) mfumo umeingizwa na hauonyeshe tabia ya oscillatory.
- Ikiwa mfumo\(b^2−4mk=0,\) huo umepunguzwa kwa kiasi kikubwa. Haionyeshe tabia ya oscillatory, lakini kupunguza yoyote kidogo katika damping ingeweza kusababisha tabia oscillatory.
- Ikiwa\(b^2−4mk<0\), mfumo huo ni underdamped. Inaonyesha tabia ya oscillatory, lakini amplitude ya oscillations hupungua kwa muda.
Ikiwa\(f(t)≠0\), suluhisho la equation tofauti ni jumla ya suluhisho la muda mfupi na ufumbuzi wa hali ya kutosha. Suluhisho la hali ya kutosha linatawala tabia ya muda mrefu ya mfumo.
Malipo ya capacitor katika mzunguko wa mfululizo wa RLC pia inaweza kuonyeshwa na equation ya pili ya mgawo wa mgawo tofauti wa fomu\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t), \nonumber \] ambapo\(L\) inductance,\(R\) ni upinzani,\(C\) ni capacitance, na\(E(t)\) ni chanzo cha voltage.

Mlinganyo muhimu

Equation ya mwendo rahisi harmonic\[x″+ω^2x=0 \nonumber \]
Suluhisho kwa mwendo rahisi wa harmonic\[x(t)=c_1 \cos (ωt)+c_2 \sin (ωt) \nonumber \]
Aina mbadala ya suluhisho kwa SHM\[x(t)=A \sin (ωt+ϕ) \nonumber \]
Kulazimishwa harmonic harakati\[mx″+bx′+kx=f(t)\nonumber \]
Malipo katika mzunguko wa mfululizo wa RLC\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t),\nonumber \]

faharasa

Mzunguko wa mfululizo wa RLC: njia kamili ya umeme yenye kupinga, inductor, na capacitor; utaratibu wa pili, usawa wa mgawo wa mgawo wa mara kwa mara unaweza kutumika kutengeneza malipo kwenye capacitor katika mzunguko wa mfululizo wa RLC

rahisi harmonic mwendo: mwendo ulioelezwa na equation\(x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)\), kama ilivyoonyeshwa na mfumo usiojulikana wa spring ambao umati unaendelea kusonga kwa muda usiojulikana

ufumbuzi wa hali thabiti: suluhisho la usawa wa kutofautiana usio na kawaida unaohusiana na kazi ya kulazimisha; kwa muda mrefu, suluhisho linakaribia ufumbuzi wa hali ya kutosha