17.1: Ulinganisho wa Mstari wa Pili
- Page ID
- 178834
- Tambua usawa wa kutofautiana na usio na kawaida wa mstari.
- Kuamua equation tabia ya equation homogeneous linear.
- Tumia mizizi ya equation ya tabia ili kupata suluhisho la usawa wa mstari sawa.
- Tatua matatizo ya thamani ya awali na thamani ya mipaka inayohusisha equations tofauti ya mstari.
Wakati wa kufanya kazi na usawa tofauti, kwa kawaida lengo ni kupata suluhisho. Kwa maneno mengine, tunataka kupata kazi (au kazi) ambayo inatimiza equation tofauti. Mbinu tunayotumia kupata ufumbuzi huu inatofautiana, kulingana na fomu ya equation tofauti ambayo tunafanya kazi. Ulinganifu wa pili wa utaratibu una sifa kadhaa muhimu ambazo zinaweza kutusaidia kuamua njia gani ya suluhisho ya kutumia. Katika sehemu hii, sisi kuchunguza baadhi ya sifa hizi na istilahi kuhusishwa.
Ulinganifu wa mstari unaofanana
Fikiria equation tofauti ya pili
\[xy''+2x^2y'+5x^3y=0.\nonumber \]
Angalia kwamba\(y\) na derivatives yake huonekana kwa fomu rahisi. Wao ni kuzidishwa na kazi ya\(x\), lakini si kufufuliwa kwa mamlaka yoyote wenyewe, wala wao ni kuzidisha pamoja. Kama ilivyojadiliwa hapo awali, equations ya kwanza na sifa sawa inasemekana kuwa linear. Vile vile ni kweli kwa equations ya pili. Pia kumbuka kwamba maneno yote katika equation hii tofauti yanahusisha ama\(y\) au moja ya derivatives yake. Hakuna suala kuwashirikisha kazi tu ya\(x\). Ulinganisho kama huu, ambapo kila neno lina\(y\) au moja ya derivatives yake, huitwa homogeneous.
Sio equations zote tofauti zinazofanana. Fikiria equation tofauti
\[xy''+2x^2y'+5x^3y=x^2.\nonumber \]
\(x^2\)Neno upande wa kulia wa ishara sawa hauna\(y\) au yoyote ya derivatives yake. Kwa hiyo, equation hii tofauti ni nonhomogeneous.
Equation tofauti ya pili ni ya mstari ikiwa inaweza kuandikwa kwa fomu
\[a_{2}(x)y''+a){1}(x)y'+a_{0}(x)y=r(x), \label{17.1} \]
wapi\(a_{2}(x), a_{1}(x), a_{0}(x),\) na\(r(x)\) ni kazi halisi yenye thamani na\(a_{2}(x)\) si identically sifuri. Kama\(r(x) \equiv 0\) - kwa maneno mengine, kama\(r(x)=0\) kwa kila thamani\(x\) ya-equation inasemekana kuwa homogeneous linear equation. Kama\(r(x) \neq 0\) kwa baadhi ya thamani ya equation\(x,\) inasemekana kuwa nonhomogeneous linear equation.
Katika equations tofauti ya mstari,\(y\) na derivatives zake zinaweza kuinuliwa tu kwa nguvu ya kwanza na haziwezi kuzidishwa kwa kila mmoja. Masharti yanayohusisha\(y^2\) au\(\sqrt{y'}\) kufanya equation nonlinear. Kazi\(y\) na derivatives yake, kama vile\(\sin y\) au\(e^{y'}\), ni marufuku sawa katika equations tofauti ya mstari.
Kumbuka kuwa equations haiwezi kutolewa kwa fomu ya kawaida (fomu iliyoonyeshwa katika ufafanuzi). Inaweza kuwa na manufaa kwa kuandika upya katika fomu hiyo kuamua kama wao ni linear, au kama equation linear ni homogeneous.
Kuainisha kila moja ya equations zifuatazo kama linear au nonlinear. Kama equation ni linear, kuamua zaidi kama ni homogeneous au nonhomogeneous.
- \(y''+3x^4y'+x^2y^2=x^3\)
- \((\sin x)y''+(\cos x)y'+3y=0\)
- \(4t^2x''+3txx'+4x=0\)
- \(5y''+y=4x^5 \)
- \(( \cos x)y''- \sin y'+( \sin x)y- \cos x=0\)
- \(8ty''-6t^2y'+4ty-3t^2=0 \)
- \( \sin(x^2)y''-( \cos x)y'+x^2y=y'-3 \)
- \(y''+5xy'-3y= \cos y\)
Suluhisho
- Equation hii ni nonlinear kwa sababu ya\(y^2\) neno.
- Equation hii ni linear. Hakuna neno linalohusisha nguvu au kazi ya\(y,\) na coefficients ni kazi zote za\(x\) .Equation tayari imeandikwa katika fomu ya kawaida, na\(r(x)\) ni sawa na sifuri, hivyo equation ni sawa.
- Equation hii ni nonlinear. Kumbuka kwamba, katika kesi hii,\(x\) ni variable tegemezi na\(t\) ni variable huru. Muda wa pili unahusisha bidhaa ya\(x\) na\(x'\), hivyo equation ni nonlinear.
- Equation hii ni linear. Tangu\(r(x)=4x^5,\) equation ni nonhomogeneous.
- Equation hii ni nonlinear, kwa sababu ya\(\sin y'\) neno.
- Equation hii ni linear. Kuandika upya katika fomu ya kawaida inatoa
\[8t^2y''-6t^2y'+4ty=3t^2. \nonumber \]
Pamoja na equation katika hali ya kiwango, tunaweza kuona kwamba\(r(t)=3t^2,\) hivyo equation ni nonhomogeneous. - Equation Hii inaonekana kama ni linear, lakini tunapaswa kuandika upya katika hali ya kiwango kuwa na uhakika. Tunapata
\[ \sin(x^2)y''-(\cos x+1)y'+x^2y=-3. \nonumber \]
Equation hii ni, kwa kweli, linear. Pamoja na\(r(x)=-3,\) hayo ni nonhomogeneous. - Equation hii ni nonlinear kwa sababu ya\(\cos y\) neno.
Kuainisha kila moja ya equations zifuatazo kama linear au nonlinear. Kama equation ni linear, kuamua zaidi kama ni homogeneous au nonhomogeneous.
- \((y'')2-y'+8x^3y=0\)
- \((\sin t)y''+ \cos t-3ty'=0\)
- Kidokezo
-
Andika equation katika fomu ya kawaida (Equation\ ref {17.1}) ikiwa ni lazima. Angalia kwa nguvu au kazi za\(y\) na derivatives yake.
- Jibu
-
Nonlinear
- Jibu b
-
isiyo ya kawaida
Baadaye katika sehemu hii, tutaona baadhi ya mbinu za kutatua aina maalum za equations tofauti. Kabla ya kupata kwamba, hata hivyo, hebu kupata kujisikia kwa jinsi ufumbuzi wa equations linear tofauti kuishi. Mara nyingi, kutatua equations tofauti inategemea kufanya nadhani elimu juu ya nini ufumbuzi inaweza kuonekana kama. Kujua jinsi aina mbalimbali za ufumbuzi zinavyofanya zitasaidia.
Fikiria usawa wa mstari, sawa na uwiano
\[x^2y''-xy′-3y=0. \nonumber \]
Kuangalia equation hii, taarifa kwamba kazi mgawo ni polynomials, na mamlaka ya juu ya\(x\) kuhusishwa na derivatives juu-ili ya\(y\). Onyesha kwamba\(y=x^3\) ni suluhisho la equation hii tofauti.
Suluhisho
Hebu\(y=x^3.\) Kisha\(y'=3x^2\) na\(y''=6x.\) Kubadilisha katika equation tofauti, tunaona kwamba
\[\begin{align*} x^2y''-xy'-3y &=x^2(6x)-x(3x^2)-3(x^3) \\[4pt] &=6x^3-3x^3-3x^3 \\[4pt] &=0. \end{align*}\]
Onyesha kwamba\(y=2x^2\) ni suluhisho la equation tofauti
\[\dfrac{1}{2}x^2y''-xy'+y=0. \label{ex2} \]
- Kidokezo
-
Kuhesabu derivatives na badala yao katika equation tofauti.
- Jibu
-
Hii inahitaji kuhesabu\(y'\) na\(y''\).
\[y' = \dfrac{dy}{dx} = 4x \nonumber \]
na
\[ y'' = \dfrac{dy'}{dx} = 4 \nonumber \]
Kuingiza derivatives hizi pamoja na\(y=2x^2\) katika Equation\ ref {ex2}.
\[\begin{align*} \dfrac{1}{2}x^2y''-xy'+y &\overset{?}{=} 0 \\[4pt] \dfrac{1}{2}x^2(4) - x (4x) + 2x^2 &\overset{?}{=} 0 \\[4pt] 2x^2 - 4x^2 + 2x^2 &\overset{\checkmark}{=} 0 \end{align*} \nonumber \]
Ndiyo, hii ni suluhisho la equation tofauti katika Equation\ ref {ex2}.
Ingawa tu kutafuta ufumbuzi wowote wa equation tofauti ni muhimu, wanahisabati na wahandisi mara nyingi wanataka kwenda zaidi ya kutafuta suluhisho moja kwa equation tofauti kutafuta ufumbuzi wote kwa equation tofauti. Kwa maneno mengine, tunataka kupata suluhisho la jumla. Kama ilivyo na equations tofauti ya kwanza, suluhisho la jumla (au familia ya ufumbuzi) hutoa seti nzima ya ufumbuzi kwa equation tofauti. Tofauti muhimu kati ya equations ya kwanza na ya pili ni kwamba, pamoja na equations ya pili ili, sisi kawaida haja ya kupata ufumbuzi mbili tofauti kwa equation kupata ufumbuzi wa jumla. Ikiwa tunapata ufumbuzi wawili, basi mchanganyiko wowote wa mstari wa ufumbuzi huu pia ni suluhisho. Tunasema ukweli huu kama theorem ifuatayo.
Kama\(y_1(x)\) na\(y_2(x)\) ni ufumbuzi wa equation linear homogeneous tofauti, basi kazi
\[y(x)=c_1y_1(x)+c_2y_2(x), \label{super} \]
wapi\(c_1\) na\(c_2\) ni mara kwa mara, pia ni suluhisho.
Ushahidi wa theorem hii ya kanuni ya superposition imesalia kama zoezi.
Fikiria equation tofauti
\[y''-4y'-5y=0.\nonumber \]
Kutokana\(e^{-x}\) na kwamba na\(e^{5x}\) ni ufumbuzi wa equation hii tofauti, kuonyesha kwamba\(4e^{-x}+e^{5x}\) ni suluhisho.
Suluhisho
Ingawa hii inaweza kufanyika kupitia matumizi rahisi ya kanuni ya Superposition (Equation\ ref {super}), lakini tunaweza pia kuthibitisha ni suluhisho kupitia mbinu kama katika Mfano\(\PageIndex{2}\). Tuna
\[ \begin{align*} y(x) &=4e^{-x}+e^{5x} \\[4pt] y'(x) &= -4e^{-x} + 5e^{5x} \\[4pt] y''(x) &=4e^{-x}+25e^{5x}. \end{align*}\]
Kisha
\[\begin{align*} y''-4y'-5y &\overset{?}{=} (4e^{-x}+25e^{5x})-4(-4e^{-x}+5e^{5x})-5(4e^{-x}+e^{5x}) \\[4pt] &\overset{?}{=} 4e^{-x}+25e^{5x}+16e^{-x}-20e^{5x}-20e^{-x}-5e^{5x} \\[4pt] &\overset{\checkmark}{=}0. \end{align*} \nonumber \]
Hivyo,\(y(x)=4e^{-x}+e^{5x}\) ni suluhisho.
Fikiria equation tofauti
\[y''+5y'+6y=0. \nonumber \]
Kutokana\(e^{-2x}\) na kwamba na\(e^{-3x}\) ni ufumbuzi wa equation hii tofauti, kuonyesha kwamba\(3e^{-2x}+6e^{-3x}\) ni suluhisho.
- Kidokezo
-
Tofautisha kazi na mbadala katika equation tofauti.
- Jibu
-
Ingawa hii inaweza kuwa matumizi rahisi ya kanuni ya Superposition (Equation\ ref {super}), tunaweza pia kuweka kupitia hiyo kama katika Mfano\(\PageIndex{2}\). Tuna
\[ \begin{align*} y(x) &=3e^{-2x}+6e^{-3x} \\[4pt] y'(x) &= -6 e^{-2x} - 18e^{-3x} \\[4pt] y''(x) &= 12e^{-2x} + 54e^{3x}. \end{align*}\]
Kisha
\[\begin{align*} y''+5y'+6y &= (12e^{-2x} + 54e^{3x}) + 5( -6 e^{-2x} - 18e^{-3x} ) + 6( 3e^{-2x} + 6e^{3x}) \\[4pt] &\overset{?}{=} \cancel{12e^{-2x}} + \bcancel{54e^{3x}} - \cancel{30e^{-2x}} - \bcancel{90e^{3x}} + \cancel{18e^{-2x}} + \bcancel{36e^{3x}} \\[4pt] &\overset{\checkmark}{=}0. \end{align*} \nonumber \]
Hivyo,\(3e^{-2x}+6e^{-3x}\) ni ufumbuzi wa equation tofauti
Kwa bahati mbaya, ili kupata suluhisho la jumla kwa equation tofauti ya pili, haitoshi kupata ufumbuzi wowote wawili na kisha kuchanganya. Fikiria equation tofauti
\[x''+7x'+12x=0.\nonumber \]
Wote\(e^{-3t}\) na\(2e^{-3t}\) ni ufumbuzi (unaweza kuangalia hii). Hata hivyo,
\[x(t)=c_1e^{-3t}+c_2(2e^{-3t})\nonumber \]
si ufumbuzi wa jumla. Maneno haya haina akaunti kwa ufumbuzi wote wa equation tofauti. Hasa, inashindwa kuhesabu kazi\(e^{-4t},\) ambayo pia ni suluhisho la equation tofauti. Inageuka kuwa ili kupata suluhisho la jumla kwa usawa wa pili wa tofauti, tunapaswa kupata ufumbuzi wa kujitegemea wa mstari. Tunafafanua istilahi hiyo hapa.
Seti ya kazi\(f_1(x),\, f_2(x), \ldots ,f_n(x)\) inasemekana kuwa tegemezi linearly ikiwa kuna mara kwa mara\(c_1,\, c_2, \ldots c_n,\), sio sifuri zote, kama vile
\[c_1f_1(x)+c_2f_2(x)+ \cdots +c_nf_n(x)=0 \nonumber \]
kwa wote\(x\) juu ya muda wa riba. Seti ya kazi ambayo si tegemezi linearly inasemekana kuwa linearly kujitegemea.
Katika sura hii, sisi kawaida mtihani seti ya kazi mbili tu kwa ajili ya uhuru linear, ambayo inaruhusu sisi kurahisisha ufafanuzi huu. Kutokana na mtazamo wa vitendo, tunaona kwamba kazi mbili ni tegemezi linearly kama mmoja wao ni identically sifuri au kama wao ni mara kwa mara multiples ya kila mmoja.
Kwanza tunaonyesha kwamba ikiwa kazi zinakidhi masharti yaliyotolewa hapo awali, basi hutegemea mstari. Kama moja ya kazi ni identically sifuri-kusema,\(f_2(x) \equiv 0\) -kisha kuchagua\(c_1=0\)\(c_2=1,\) na hali ya utegemezi linear ni kuridhika. Ikiwa, kwa upande mwingine,\(f_1(x)\) wala\(f_2(x)\) sio sifuri sawa, lakini\(f_1(x)=Cf_2(x)\) kwa mara kwa mara\(C,\) kisha chagua\(c_1=C\)\(c_2=-1,\) na tena, hali hiyo imeridhika.
Ifuatayo, tunaonyesha kwamba ikiwa kazi mbili zinategemea mstari, basi moja ni sawa na sifuri au ni mara kwa mara nyingi ya kila mmoja. Fikiria\(f_1(x)\) na\(f_2(x)\) ni linearly kujitegemea. Kisha, kuna constants,\(c_1\) na\(c_2,\) si wote sifuri, vile kwamba
\[c_1f_1(x)+c_2f_2(x)=0 \nonumber \]
kwa wote\(x\) juu ya muda wa riba. Kisha,
\[c_1f_1(x)=-c_2f_2(x). \nonumber \]
Sasa, tangu sisi alisema kuwa\(c_1\) na\(c_2\) hawezi wote kuwa sifuri, kudhani\(c_2 \neq 0.\) Kisha, kuna kesi mbili: ama\(c_1=0\) au\(c_1\neq 0.\) Kama\(c_1=0,\) basi
\[\begin{align*} 0 &=-c_2f_2(x) \\[4pt] 0 &=f_2(x), \end{align*}\]
hivyo moja ya kazi ni identically sifuri. Sasa tuseme\(c_1 \neq 0.\) Basi,
\[f_1(x)=\left(- \dfrac{c_2}{c_1}\right)f_2(x) \nonumber \]
na tunaona kwamba kazi ni mara kwa mara nyingi ya mtu mwingine.
Kazi mbili,\(f_1(x)\) na\(f_2(x),\) zinasemekana kuwa tegemezi linearly kama mmoja wao ni identically sifuri au kama\(f_1(x)=Cf_2(x)\) kwa baadhi ya mara kwa mara\(C\) na kwa wote\(x\) juu ya muda wa riba. Kazi ambazo si tegemezi linearly zinasemekana kuwa linearly kujitegemea.
Kuamua kama jozi zifuatazo za kazi zinategemea mstari au kujitegemea kwa mstari.
- \(f_1(x)=x^2\)na\(f_2(x)=5x^2\)
- \(f_1(x)= \sin x\)na\(f_2(x)= \cos x\)
- \(f_1(x)=e^{3x}\)na\(f_2(x)=e^{-3x}\)
- \(f_1(x)=3x\)na\(f_2(x)=3x+1\)
Suluhisho
- \(f_2(x)=5f_1(x),\)hivyo kazi ni tegemezi linearly.
- Hakuna mara kwa mara\(C\) kama\(f_1(x)=Cf_2(x),\) hivyo kazi ni linearly kujitegemea.
- Hakuna mara kwa mara\(C\) kama\(f_1(x)=Cf_2(x),\) hivyo kazi ni linearly kujitegemea. Je, si kupata kuchanganyikiwa na ukweli kwamba exponents ni nyingi mara kwa mara ya kila mmoja. Pamoja na kazi mbili za kielelezo, isipokuwa vielelezo ni sawa, kazi ni linearly kujitegemea.
- Hakuna mara kwa mara\(C\) kama\(f_1(x)=Cf_2(x),\) hivyo kazi ni linearly kujitegemea.
Kuamua kama jozi zifuatazo za kazi ni tegemezi linearly au linearly kujitegemea:\(f_1(x)=e^{x}\) na\(f_2(x)=3e^{3x}.\)
- Kidokezo
-
Je, kazi ni mara kwa mara nyingi za kila mmoja?
- Jibu
-
kujitegemea kwa mstari
Ikiwa tunaweza kupata ufumbuzi wa kujitegemea kwa mstari wa pili wa equation tofauti, basi tunaweza kuchanganya ili kupata suluhisho la jumla. Matokeo haya yameelezwa rasmi katika theorem ifuatayo.
Ikiwa\(y_1(x)\) na\(y_2(x)\) ni ufumbuzi wa kujitegemea kwa mstari wa pili, mstari, usawa wa kutofautiana, basi suluhisho la jumla linatolewa na
\[y(x)=c_1y_1(x)+c_2y_2(x), \nonumber \]
wapi\(c_1\) na\(c_2\) ni mara kwa mara.
Tunaposema familia ya kazi ni suluhisho la jumla kwa equation tofauti, tunamaanisha kwamba
- kila usemi wa fomu hiyo ni suluhisho na
- kila suluhisho la equation tofauti linaweza kuandikwa kwa fomu hiyo, ambayo inafanya theorem hii yenye nguvu sana.
Kama tunaweza kupata mbili linearly kujitegemea ufumbuzi ili pili tofauti equation, tuna, kwa ufanisi, kupatikana ufumbuzi wote kwa pili ili tofauti equation-kabisa taarifa ya ajabu. Ushahidi wa theorem hii ni zaidi ya upeo wa maandishi haya.
Ikiwa\(y_1(t)=e^{3t}\) na\(y_2(t)=e^{-3t}\) ni ufumbuzi wa suluhisho la jumla?\(y''-9y=0,\)
Suluhisho
Kumbuka kuwa\(y_1\) na\(y_2\) sio mara nyingi za kila mmoja, kwa hiyo wao ni kujitegemea kwa mstari. Kisha, ufumbuzi wa jumla wa equation tofauti ni
\(y(t)=c_1e^{3t}+c_2e^{-3t}.\)
Ikiwa\(y_1(x)=e^{3x}\) na\(y_2(x)=xe^{3x}\) ni ufumbuzi wa suluhisho la jumla?\(y''-6y'+9y=0,\)
- Kidokezo
-
Angalia uhuru wa mstari kwanza.
- Jibu
-
\(y(x)=c_1e^{3x}+c_2xe^{3x}\)
Ulinganisho wa Pili wa Amri na Coefficients ya Mara
Sasa kwa kuwa tuna hisia bora kwa usawa wa kutofautiana kwa mstari, tutazingatia kutatua equations ya pili ya fomu
\[ay''+by'+cy=0, \tag{17.2} \]
wapi\(a, b,\) na\(c\) ni mara kwa mara.
Kwa kuwa coefficients zote ni mara kwa mara, ufumbuzi huenda kuwa kazi na derivatives ambayo ni mara kwa mara nyingi wao wenyewe. Tunahitaji masharti yote kufuta nje, na kama kuchukua derivative utangulizi mrefu ambayo si mara kwa mara nyingi ya kazi ya awali, ni vigumu kuona jinsi neno hilo cancels nje. Kazi za kielelezo zina derivatives ambazo ni mara kwa mara nyingi za kazi ya awali, basi hebu tuone kinachotokea tunapojaribu suluhisho la fomu\(y(x)=e^{ \lambda x}\), ambapo\(\lambda\) (barua ya Kigiriki ya chini ya lambda) ni mara kwa mara.
Ikiwa\(y(x)=e^{ \lambda x}\), basi\(y'(x)= \lambda e^{ \lambda x}\) na\(y''= \lambda^2 e^{ \lambda x}.\) Kubadilisha maneno haya katika Equation\ ref {17.1}, tunapata
\[\begin{align*} ay''+by'+cy &= a(\lambda^2e^{\lambda x})+b(\lambda e^{\lambda x})+ce^{\lambda x} \\[4pt] &=e^{\lambda x}(a \lambda^2+b \lambda +c). \end{align*}\]
Kwa kuwa\(e\lambda x\) ni kamwe sifuri, maneno haya yanaweza kuwa sawa na sifuri kwa wote\(x\) tu kama
\[a\lambda 2+b\lambda +c=0. \nonumber \]
Tunaita hii equation ya tabia ya equation tofauti.
equation tabia ya pili ili tofauti equation\(ay''+by'+cy=0\) ni
\[a\lambda^2+b\lambda +c=0. \nonumber \]
Equation ya tabia ni muhimu sana katika kutafuta ufumbuzi wa equations tofauti ya fomu hii. Tunaweza kutatua equation tabia ama kwa factoring au kwa kutumia formula quadratic
\[\lambda = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}. \nonumber \]
Hii inatoa kesi tatu. Equation tabia ina
- mizizi halisi ya kweli;
- moja, mara kwa mara mizizi halisi; au
- mizizi tata conjugate.
Tunazingatia kila kesi hizi tofauti.
Uchunguzi wa 1: Mizizi ya Real Tofauti
Ikiwa equation ya tabia ina mizizi halisi ya kweli\(\lambda_1\) na\(\lambda_2\), basi\(e^{\lambda_1x}\) na\(e^{\lambda_2x}\) ni ufumbuzi wa kujitegemea kwa Mfano\ ref {17.1}, na suluhisho la jumla linatolewa na
\[y(x)=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}, \nonumber \]
wapi\(c_1\) na\(c_2\) ni mara kwa mara.
Kwa mfano, equation tofauti\(y''+9y'+14y=0\) ina kuhusishwa tabia equation\(\lambda^2+9\lambda+14=0.\) Hii mambo\((\lambda +2)(\lambda +7)=0,\) ambayo ina mizizi\(\lambda_1=-2\) na\(\lambda_2=-7.\) Kwa hiyo, ufumbuzi wa jumla wa equation hii tofauti ni
\[y(x)=c_1e^{-2x}+c_2e^{-7x}. \nonumber \]
Uchunguzi wa 2: Mizizi halisi ya Mara kwa mara
Mambo ni ngumu zaidi kidogo kama equation tabia ina mara kwa mara mizizi halisi,\(\lambda\). Katika kesi hii, tunajua\(e^{\lambda x}\) ni suluhisho la Equation\ ref {17.1}, lakini ni suluhisho moja tu na tunahitaji ufumbuzi wa kujitegemea wa mstari ili kuamua suluhisho la jumla. Tunaweza kujaribiwa kujaribu kazi ya fomu\(ke^{\lambda x},\) ambapo\(k\) ni baadhi ya mara kwa mara, lakini ingekuwa si linearly huru ya\(e^{\lambda x}.\) Kwa hiyo, hebu jaribu\(xe^{\lambda x}\) kama ufumbuzi wa pili. Kwanza, kumbuka kuwa kwa formula ya quadratic,
\[\lambda = \frac{-b \pm \sqrt{b^2-4ac}}{2a}. \nonumber \]
Lakini,\(\lambda\) ni mzizi mara kwa mara, hivyo ubaguzi (\(b^2-4ac\)) ni sifuri na\(\lambda = \frac{-b}{2a}\). Hivyo, kama\(y=xe^{\lambda x}\), tuna
\[\begin{align*} y' =e^{\lambda x}+ \lambda xe^{\lambda x} \\[4pt] y'' =2\lambda e^{\lambda x}+\lambda^2xe^{\lambda x}. \end{align*}\]
Kubadilisha maneno yote katika Equation\ ref {17.1}, tunaona kwamba
\[\begin{align*} ay''+by′+cy &=a(2λe^{λx}+λ^2xe^{λx})+b(e^{λx}+λxe^{λx})+cxe^{λx} \\[4pt] &=xe^{λx}(aλ^2+bλ+c)+e^{λx}(2aλ+b) \\[4pt] &=xe^{λx}(0)+e^{λx}(2a(−b2a)+b)\\[4pt] &=0+e^{λx}(0) \\[4pt] &\overset{\checkmark}{=}0. \end{align*}\]
Hii inaonyesha kwamba\(xe^{\lambda x}\) ni suluhisho la Equation\ ref {17.1}. Kwa kuwa\(e^{\lambda x}\) na\(xe^{\lambda x}\) ni kujitegemea kwa mstari, wakati equation ya tabia ina mizizi ya mara kwa mara\(\lambda \), suluhisho la jumla la Equation\ ref {17.1} hutolewa na
\[y(x)=c_1e^{\lambda x}+c_2xe^{\lambda x}, \nonumber \]
wapi\(c_1\) na\(c_2\) ni mara kwa mara.
Kwa mfano, equation tofauti\(y''+12y'+36y=0\) ina kuhusishwa tabia equation
\[\lambda^2+12 \lambda +36=0.\nonumber \]
Sababu hii\((\lambda +6)^2=0,\) ambayo ina mizizi ya mara kwa mara\(\lambda =-6\). Kwa hiyo, ufumbuzi wa jumla wa equation hii tofauti ni
\[y(x)=c_1e^{-6x}+c_2xe^{-6x}.\nonumber \]
Uchunguzi wa 3: Mizizi ya Kuunganisha Complex
Kesi ya tatu tunapaswa kuzingatia ni wakati\(b^2-4ac <0.\) Katika kesi hii, tunapotumia formula ya quadratic, tunachukua mizizi ya mraba ya namba hasi. Ni lazima kutumia idadi imaginary\( i= \sqrt{-1}\) kupata mizizi, ambayo kuchukua fomu\(\lambda_1= \alpha + \beta i \) na\(\lambda _2=\alpha -\beta i.\) idadi tata\( \alpha +\beta i\) inaitwa conjugate ya\( \alpha -\beta i\). Kwa hiyo, tunaona kwamba wakati ubaguzi\(b^2-4ac\) ni hasi, mizizi ya equation yetu ya tabia ni daima ngumu conjugates.
Hii inajenga kidogo ya tatizo kwa ajili yetu. Kama sisi kufuata mchakato huo sisi kutumika kwa tofauti mizizi halisi-kutumia mizizi ya equation tabia kama coefficients katika exponents ya kazi kielelezo - sisi kupata kazi\(e^{(\alpha + \beta i)x}\) na\(e^{(\alpha - \beta i)x}\) kama ufumbuzi wetu. Hata hivyo, kuna matatizo na njia hii. Kwanza, kazi hizi zinachukua maadili magumu (ya kufikiri), na majadiliano kamili ya kazi hizo ni zaidi ya upeo wa maandiko haya. Pili, hata kama tulikuwa na starehe na kazi tata za thamani, katika kozi hii hatuwezi kushughulikia wazo la derivative kwa kazi hizo. Hivyo, kama inawezekana, tungependa kupata mbili linearly kujitegemea halisi ya thamani ufumbuzi kwa equation tofauti. Kwa madhumuni ya maendeleo haya, sisi ni kwenda kuendesha na kutofautisha kazi\(e^{(\alpha + \beta i)x}\) na\(e^{(\alpha - \beta i)x}\) kama walikuwa halisi thamani kazi. Kwa kazi hizi hasa, mbinu hii ni halali hesabu, lakini kuwa na ufahamu kwamba kuna matukio mengine wakati kazi tata thamani wala kufuata sheria sawa na kazi halisi thamani. Wale wenu wanaopenda majadiliano ya kina zaidi ya kazi za thamani tata wanapaswa kushauriana na maandishi ya uchambuzi tata.
Kulingana na mizizi\(\alpha \pm \beta i\) ya equation ya tabia, kazi\(e^{(\alpha + \beta i)x}\) na\(e^{(\alpha - \beta i)x}\) ni ufumbuzi wa kujitegemea kwa usawa tofauti na ufumbuzi wa jumla hutolewa na
\[y(x)=c_1e^{(\alpha +\beta i)x}+c_2e^{(\alpha - \beta i)x}. \nonumber \]
Kutumia baadhi ya uchaguzi smart kwa\(c_1\) na\(c_2\), na kidogo ya kudanganywa algebraic, tunaweza kupata mbili linearly kujitegemea, halisi ya thamani ufumbuzi kwa Equation\ ref {17.1} na kueleza ufumbuzi wetu wa jumla katika maneno hayo.
Tulikutana na kazi za kielelezo na vielelezo vingi mapema. Moja ya zana muhimu tulizotumia kueleza kazi hizi kielelezo katika suala la sines na cosines ilikuwa formula Euler, ambayo inatuambia kwamba
\[\underbrace{e^{i \theta }= \cos \theta+ i \sin \theta}_{\text{Euler’s formula}} \label{Euler} \]
kwa idadi yote halisi\(\theta \).
Kurudi nyuma ya ufumbuzi wa jumla, tuna
\[\begin{align*} y(x) &=c_1e^{( \alpha+ \beta i)x}+c_2e^{(\alpha - \beta i)x} \\[4pt] &=c_1e^{\alpha x}e^{\beta ix}+c_2e^{\alpha x}e^{- \beta ix} \\[4pt] &=e^{\alpha x}(c_1e^{\beta ix}+c_2e^{-\beta ix}).\end{align*}\]
Kutumia formula ya Euler (Equation\ ref {Euler}) pamoja na utambulisho\(\cos(-x)=\cos x\) na\(\sin(-x)=- \sin x,\) tunapata
\[\begin{align} y(x) &=e^{\alpha x}[c_1(\cos \beta x+i \sin \beta x)+c_2(\cos(- \beta x)+i \sin(- \beta x))] \nonumber \\[4pt] &=e^{\alpha x}[(c_1+c_2)\cos \beta x+(c_1-c_2)i \sin \beta x]. \label{E1}\end{align} \]
Sasa, kama sisi kuchagua muda\(c_1=c_2= \frac{1}{2},\) wa pili ni sifuri na sisi kupata
\[y(x)=e^{\alpha x} \cos \beta x \nonumber \]
kama suluhisho la thamani halisi kwa Equation\ ref {17.1}. Vile vile, kama sisi kuchagua\(c_1=−\frac{i}{2}\) na\(c_2=\frac{i}{2}\), mrefu ya kwanza ya Equation\ ref {E1} ni sifuri na sisi kupata
\[y(x)=e^{\alpha x} \sin \beta x \nonumber \]
kama pili, linearly kujitegemea, halisi thamani ufumbuzi kwa Equation\ ref {17.1}.
Kulingana na hili, tunaona kwamba ikiwa equation ya tabia ina mizizi ngumu ya conjugate\(\alpha \pm \beta i,\) basi suluhisho la jumla la Equation\ ref {17.1} hutolewa na
\[\begin{align*} y(x) &=c_1e^{\alpha x} \cos \beta x+c_2e^{\alpha x} \sin \beta x \\[4pt] &=e^{\alpha x}(c_1 \cos \beta x+c_2 \sin \beta x),\end{align*}\]
wapi\(c_1\) na\(c_2\) ni mara kwa mara.
Kwa mfano, equation tofauti\(y''-2y'+5y=0\) ina kuhusishwa tabia equation\(\lambda ^2-2 \lambda +5=0.\) Kwa formula quadratic, mizizi ya equation tabia ni\(1\pm 2i.\) Kwa hiyo, ufumbuzi wa jumla wa equation hii tofauti ni
\[y(x)=e^{x}(c_1 \cos 2x+c_2 \sin 2x).\nonumber \]
Muhtasari wa Matokeo
Tunaweza kutatua utaratibu wa pili, mstari, usawa wa kutofautiana na coefficients mara kwa mara kwa kutafuta mizizi ya equation ya tabia inayohusishwa. Aina ya suluhisho la jumla inatofautiana, kulingana na kwamba equation ya tabia ina tofauti, mizizi halisi; mizizi moja, mara kwa mara halisi; au mizizi tata ya conjugate. Matukio matatu yanafupishwa katika Jedwali\(\PageIndex{1}\).
| Mizizi ya equation tabia | Suluhisho la jumla kwa usawa tofauti |
|---|---|
| Tofauti mizizi halisi,\(\lambda_1\) na\(\lambda_2\) | \(y(x)=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}\) |
| Mizizi halisi ya mara kwa mara,\(\lambda \) | \(y(x)=c_1e^{\lambda x}+c_2xe^{\lambda x}\) |
| Mizizi ngumu ya conjugate\(\alpha \pm \beta i\) | \(y(x)=e^{\alpha x}(c_1 \cos \beta x+c_2 \sin \beta x)\) |
- Andika equation tofauti katika fomu\(a''+by'+cy=0.\)
- Kupata sambamba tabia equation\(a\lambda^2+b\lambda +c=0.\)
- Aidha sababu equation tabia au kutumia formula quadratic kupata mizizi.
- Kuamua fomu ya suluhisho la jumla kulingana na kama equation ya tabia ina tofauti, mizizi halisi; moja, mara kwa mara mizizi halisi; au mizizi tata ya conjugate.
Pata suluhisho la jumla kwa equations tofauti zifuatazo. Kutoa majibu yako kama kazi ya\(x\).
- \(y''+3y'-4y=0\)
- \(y''+6y'+13y=0\)
- \(y''+2y'+y=0\)
- \(y''-5y'=0\)
- \(y''-16y=0\)
- \(y''+16y=0\)
Suluhisho
Kumbuka kwamba equations hizi zote tayari zimetolewa kwa fomu ya kawaida (hatua ya 1).
- Equation ya tabia ni\(\lambda^2+3\lambda -4=0\) (hatua ya 2). Hii sababu katika\((\lambda +4)(\lambda -1)=0\), hivyo mizizi ya equation tabia ni\(\lambda_1=-4\) na\(\lambda_2=1\) (hatua 3). Kisha ufumbuzi wa jumla wa equation tofauti ni
\[y(x)=c_1e^{-4x}+c_2e^{x}. \tag{step 1} \]
- Equation ya tabia ni\(\lambda^2+6\lambda+13=0\) (hatua ya 2). Kutumia formula ya quadratic, tunaona equation hii ina mizizi tata conjugate\(-3\pm 2i\) (hatua ya 3). Kisha ufumbuzi wa jumla wa equation tofauti ni
\[y(t)=e^{-3t}(c_1 \cos 2t+c_2 \sin 2t). \tag{step 2} \]
- Equation ya tabia ni\(\lambda^2+2\lambda+1=0\) (hatua ya 2). Sababu hii katika\((\lambda+1)2=0,\) hivyo equation tabia ina mara kwa mara mizizi halisi\(\lambda =-1\) (hatua 3). Kisha ufumbuzi wa jumla wa equation tofauti ni
\[y(t)=c_1e^{-t}+c_2te^{-t}. \tag{step 3} \]
- Equation ya tabia ni\(\lambda^2-5\lambda\) (hatua ya 2). Hii husababisha\(\lambda(\lambda -5)=0,\) hivyo mizizi ya equation ya tabia ni\(\lambda_1=0\) na\(\lambda_2=5\) (hatua ya 3). Kumbuka kwamba\(e^{0x}=e^{0}=1\), hivyo suluhisho letu la kwanza ni mara kwa mara tu. Kisha ufumbuzi wa jumla wa equation tofauti ni
\[y(x)=c_1+c_2e^{5x}. \tag{step 4} \]
- Equation ya tabia ni\(\lambda^2-16=0\) (hatua ya 2). Hii husababisha\((\lambda+4)(\lambda -4)=0,\) hivyo mizizi ya equation ya tabia ni\(\lambda_1=4\) na\(\lambda_2=-4\) (hatua ya 3). Kisha ufumbuzi wa jumla wa equation tofauti ni
\[y(x)=c_1e^{4x}+c_2e^{-4x}. \tag{step 5} \]
- Equation ya tabia ni\(\lambda^2+16=0\) (hatua ya 2). Hii ina mizizi ngumu ya conjugate\(\pm 4i\) (hatua ya 3). Kumbuka kwamba\(e^{0x}=e^0=1\), hivyo neno kielelezo katika suluhisho letu ni mara kwa mara tu. Kisha ufumbuzi wa jumla wa equation tofauti ni
\[y(t)=c_1 \cos 4t+c_2 \sin 4t. \tag{step 6} \]
Pata suluhisho la jumla kwa equations tofauti zifuatazo:
- \(y''-2y'+10y=0\)
- \(y''+14y'+49y=0\)
- Kidokezo
-
Pata mizizi ya equation ya tabia.
- Jibu
-
\(y(x)=e^x(c_1 \cos 3x+c_2 \sin 3x)\)
- Jibu b
-
\(y(x)=c_1e^{-7x}+c_2xe^{-7x}\)
Matatizo ya Thamani ya awali na Matatizo ya Thamani ya Mpaka
Hadi sasa, tumekuwa tukipata ufumbuzi wa jumla wa equations tofauti. Hata hivyo, milinganyo tofauti mara nyingi hutumiwa kuelezea mifumo ya kimwili, na mtu anayejifunza mfumo wa kimwili kwa kawaida anajua kitu kuhusu hali ya mfumo huo kwa pointi moja au zaidi kwa wakati. Kwa mfano, kama mara kwa mara mgawo tofauti equation ni kuwakilisha jinsi mbali pikipiki mshtuko absorber ni USITUMIE, tunaweza kujua kwamba mpanda ni kukaa bado juu ya pikipiki yake katika mwanzo wa mbio, wakati\(t=t_0.\) Hii ina maana mfumo ni katika msawazo, hivyo\(y(t_0)=0,\) na compression ya mshtuko absorber haibadilika, hivyo\(y'(t_0)=0.\) Kwa hali hizi mbili za awali na ufumbuzi wa jumla wa equation tofauti, tunaweza kupata suluhisho maalum kwa equation tofauti ambayo inatimiza hali zote mbili za awali. Utaratibu huu unajulikana kama kutatua tatizo la thamani ya awali. (Kumbuka kwamba sisi kujadili matatizo ya awali ya thamani katika Utangulizi wa tofauti equations.) Kumbuka kuwa equations ya pili ili kuwa na mbili constants holela katika suluhisho la jumla, na kwa hiyo tunahitaji hali mbili za awali ili kupata suluhisho la tatizo la thamani ya awali.
Wakati mwingine tunajua hali ya mfumo kwa nyakati mbili tofauti. Kwa mfano, tunaweza kujua\(y(t_0)=y_0\) na Masharti\(y(t_1)=y_1.\) haya huitwa hali ya mipaka, na kutafuta suluhisho la equation tofauti ambayo inatimiza hali ya mipaka inaitwa kutatua tatizo la thamani ya mipaka.
Wataalamu wa hisabati, wanasayansi, na wahandisi wanapenda kuelewa hali ambayo tatizo la thamani ya awali au tatizo la thamani ya mipaka lina suluhisho la pekee. Ingawa matibabu kamili ya mada hii ni zaidi ya upeo wa maandishi haya, ni muhimu kujua kwamba, katika mazingira ya mgawo wa mara kwa mara, equations ya pili, matatizo ya thamani ya awali yanahakikishiwa kuwa na suluhisho la kipekee kwa muda mrefu kama hali mbili za awali zinatolewa. Matatizo ya thamani ya mipaka, hata hivyo, sio vizuri. Hata wakati hali mbili za mipaka zinajulikana, tunaweza kukutana na matatizo ya thamani ya mipaka na ufumbuzi wa kipekee, ufumbuzi wengi, au hakuna ufumbuzi wowote.
Tatua tatizo la thamani ya awali:\(y''+3y'-4y=0, \, y(0)=1,\, y'(0)=-9.\)
Suluhisho
Tayari tumetatua usawa huu tofauti katika Mfano 17.6a. na kupatikana suluhisho la jumla kuwa
\[y(x)=c_1e^{-4x}+c_2e^{x}. \nonumber \]
Kisha
\[y'(x)=-4c_1e^{-4x}+c_2e^{x}. \nonumber \]
Wakati\(x=0,\) tuna\(y(0)=c_1+c_2\) na\(y'(0)=-4c_1+c_2.\) kutumia hali ya awali, tuna
\[\begin{align*} c_1+c_2 &=1 \\[4pt] -4c_1+c_2 &=-9.\end{align*}\]
Kisha\(c_1=1-c_2.\) Kubadilisha maneno haya katika equation ya pili, tunaona kwamba
\[\begin{align*} -4(1-c_2)+c_2 &= -9 \\[4pt] -4+4c_2+c_2 &=-9 \\[4pt] 5c_2 &=-5 \\[4pt] c_2 &=-1. \end{align*}\]
Hivyo,\(c_1=2\) na suluhisho la tatizo la thamani ya awali ni
\[y(x)=2e^{-4x}-e^{x}. \nonumber \]
Tatua tatizo la thamani ya awali\(y''-3y'-10y=0, \quad y(0)=0, \; y'(0)=7.\)
- Kidokezo
-
Tumia hali ya awali ili kuamua maadili\(c_1\) na\(c_2\).
- Jibu
-
\[y(x)=-e^{-2x}+e^{5x} \nonumber \]
Tatua tatizo la thamani ya awali na graph suluhisho:
\[y''+6y'+13y=0, \quad y(0)=0, \; y'(0)=2\nonumber \]
Suluhisho
Tayari tumetatua equation hii tofauti katika\(\PageIndex{6b}\) Mfano. na kupatikana suluhisho la jumla kuwa
\[y(x)=e^{-3x}(c_1 \cos 2x+c_2 \sin 2x).\nonumber \]
Kisha
\[y'(x)=e^{-3x}(-2c_1 \sin 2x+2c_2 \cos 2x)-3e^{-3x}(c_1 \cos 2x+c_2 \sin 2x). \nonumber \]
Wakati\(x=0,\) tuna\(y(0)=c_1\) na\(y'(0)=2c_2-3c_1\). Kutumia hali ya awali, tunapata
\[ \begin{align*} c_1 &=0 \\[4pt] -3c_1+2c_2 &=2. \end{align*}\]
Kwa hiyo,\(c_1=0, \, c_2=1,\) na suluhisho la tatizo la thamani ya awali linaonyeshwa kwenye grafu ifuatayo.
\[y=e^{-3x} \sin 2x.\nonumber \]
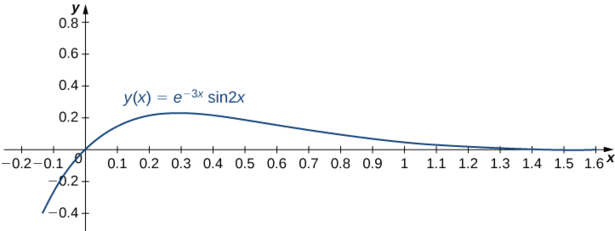
Tatua tatizo la thamani ya awali na graph suluhisho:\(y''-2y'+10y=0, \quad y(0)=2, \; y'(0)=-1\)
- Kidokezo
-
Tumia hali ya awali ili kuamua maadili\(c_1\) na\(c_2.\)
- Jibu
-
\[y(x)=e^{x}(2 \cos 3x - \sin 3x) \nonumber \]
Tatizo la thamani ya awali linalofuata mfano wa msimamo wa kitu kilicho na wingi unaohusishwa na chemchemi. Mifumo ya molekuli ya spring inachunguzwa kwa undani katika Maombi. Suluhisho la equation tofauti hutoa nafasi ya wingi kwa heshima ya nafasi ya neutral (usawa) (katika mita) wakati wowote. (Kumbuka kuwa kwa mifumo ya spring-molekuli ya aina hii, ni desturi ya kufafanua mwelekeo wa chini kama chanya.)
\[y''+2y'+y=0, \quad y(0)=1, \; y'(0)=0 \nonumber \]
Tatua tatizo la thamani ya awali na graph suluhisho. Je! Ni nafasi gani ya wingi wakati wa\(t=2\) sec? Je! Misa ya haraka inahamia wakati wa\(t=1\) sec? Katika mwelekeo gani?
Suluhisho
Katika Mfano\(\PageIndex{6c}\) Mfano. tuligundua ufumbuzi wa jumla wa equation hii tofauti kuwa
\[y(t)=c_1e^{-t}+c_2te^{-t}. \nonumber \]
Kisha
\[y'(t)=-c_1e^{-t}+c_2(-te^{-t}+e^{-t}). \nonumber \]
Wakati\(t=0,\) tuna\(y(0)=c_1\) na\(y'(0)=c_1+c_2.\) kutumia hali ya awali, tunapata
\[c_1=1 \\ -c_1+c_2=0. \nonumber \]
Hivyo,\(c_1=1, c_2=1,\) na ufumbuzi wa tatizo thamani ya awali ni
\[y(t)=e^{-t}+te^{-t}. \nonumber \]
Suluhisho hili linawakilishwa katika grafu ifuatayo. Wakati\(t=2,\) molekuli iko katika nafasi\(y(2)=e^{-2}+2e^{-2}=3e^{-2} \approx 0.406\) m chini ya usawa.
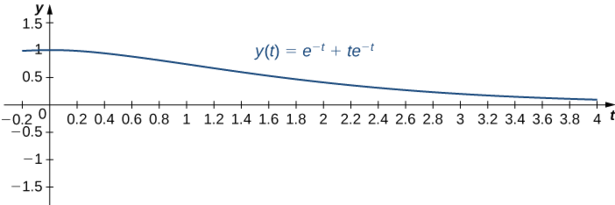
Ili kuhesabu kasi kwa wakati\(t=1,\) tunahitaji kupata derivative. Tuna\(y(t)=e^{-t}+te^{-t},\) hivyo
\[y'(t)=-e^{-t}+e^{-t}-te^{-t}= -te^{-t}. \nonumber \]
Kisha\(y'(1)=-e^{-1} \approx -0.3679\). Wakati\(t=1,\) molekuli ni kusonga juu saa\(0.3679\) m/sec.
Tuseme mifano ya tatizo la awali la thamani ya msimamo (kwa miguu) ya wingi katika mfumo wa spring wakati wowote. Tatua tatizo la thamani ya awali na graph suluhisho. Je! Ni nafasi gani ya wingi wakati wa\(t=0.3\) sec? Je, ni haraka gani kusonga wakati\(t=0.1\) sec? Katika mwelekeo gani?
\[y''+14y'+49y=0, \quad y(0)=0, \; y'(0)=1 \nonumber \]
- Kidokezo
-
Tumia hali ya awali ili kuamua maadili\(c_1\) na\(c_2\).
- Jibu
-
\[y(t)=te^{-7t}\nonumber \]
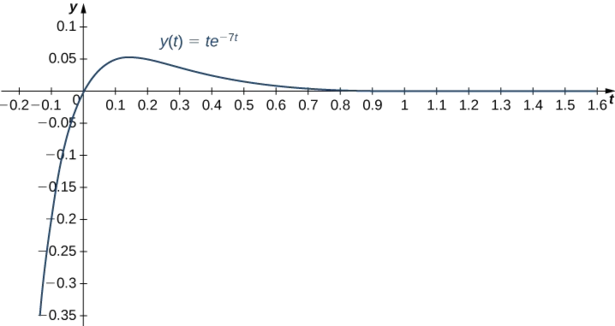
Kwa wakati\(t=0.3, \; y(0.3)=0.3e^{(-7^{\ast} 0.3)}=0.3e^{-2.1} \approx 0.0367. \) Masi ni\(0.0367\) ft chini ya usawa. Kwa wakati\(t=0.1, \; y'(0.1)=0.3e^{-0.7} \approx 0.1490.\) Masi ni kusonga chini kwa kasi ya\(0.1490\) ft/sec.
Katika Mfano 17.6f. sisi kutatuliwa tofauti equation\(y''+16y=0\) na kupatikana ufumbuzi wa jumla kuwa\(y(t)=c_1 \cos 4t+c_2 \sin 4t.\) Kama inawezekana, kutatua tatizo mipaka-thamani kama hali ya mipaka ni yafuatayo:
- \(y(0)=0, y( \frac{\pi}{4})=0\)
- \(y(0)=1,y(0)=1, y(\frac{\pi}{8})=0\)
- \(y(\frac{\pi}{8})=0, y(\frac{3 \pi}{8})=2\)
Suluhisho
Tuna
\[y(x)=c_1 \cos 4t+c_2 \sin 4t. \nonumber \]
- Kutumia kwanza mpaka hali aliyopewa hapa, sisi kupata\(y(0)=c_1=0.\) Hivyo ufumbuzi ni wa fomu\(y(t)=c_2 \sin 4t.\) Wakati sisi kuomba pili mpaka hali, ingawa, sisi kupata\(y(\frac{\pi}{4})=c_2 \sin(4(\frac{\pi}{4}))=c_2 \sin \pi =0 \) kwa maadili yote ya\(c_2\). Hali ya mipaka haitoshi kuamua thamani kwa\(c_2,\) hivyo tatizo hili la thamani ya mipaka lina ufumbuzi mkubwa sana. Hivyo,\(y(t)=c_2 \sin 4t\) ni suluhisho kwa thamani yoyote ya\(c_2\).
- Kutumia hali ya kwanza ya mipaka iliyotolewa hapa, tunapata\(y(0)=c_1=1.\) Kutumia hali ya pili ya mipaka inatoa\(y(\frac{\pi}{8})=c_2=0,\) hivyo\(c_2=0.\) Katika kesi hii, tuna ufumbuzi wa kipekee:\(y(t)= \cos 4t\).
- Kutumia hali ya kwanza ya mipaka iliyotolewa hapa, tunapata\(y(\frac{\pi}{8})=c_2=0.\) Hata hivyo, kutumia hali ya pili ya mipaka inatoa\(y(\frac{3 \pi}{8})=-c_2=2,\) hivyo\(c_2=-2.\) Hatuwezi kuwa na\(c_2=0=-2,\) tatizo hili la thamani ya mipaka halina suluhisho.
Dhana muhimu
- Ulinganifu wa pili wa utaratibu unaweza kuhesabiwa kama linear au isiyo ya kawaida, homogeneous au isiyo ya kawaida.
- Ili kupata suluhisho la jumla kwa usawa wa pili wa utaratibu wa pili, tunapaswa kupata ufumbuzi wa kujitegemea wa mstari. Ikiwa\(y_1(x)\) na\(y_2(x)\) ni ufumbuzi wa kujitegemea kwa mstari wa pili, mstari, usawa wa kutofautiana, basi suluhisho la jumla linatolewa na
\[y(x)=c_1y_1(x)+c_2y_2(x).\nonumber \]
- Ili kutatua usawa wa pili wa utaratibu wa pili na coefficients ya mara kwa mara, pata mizizi ya equation ya tabia. Aina ya suluhisho la jumla inatofautiana kulingana na kama equation ya tabia ina tofauti, mizizi halisi; moja, mara kwa mara mizizi halisi; au mizizi tata ya conjugate.
- Hali ya awali au masharti ya mipaka yanaweza kutumiwa kupata suluhisho maalum kwa equation tofauti ambayo inatimiza masharti hayo, isipokuwa wakati hakuna suluhisho au ufumbuzi mkubwa sana.
Mlinganyo muhimu
- Linear pili ili tofauti equation\[a_2(x)y''+a_1(x)y'+a_0(x)y=r(x) \nonumber \]
- Equation ya pili na coefficients mara kwa mara\[ay''+by'+cy=0 \nonumber \]
faharasa
- hali ya mipaka
- masharti ambayo hutoa hali ya mfumo kwa nyakati tofauti, kama nafasi ya mfumo wa spring-molekuli kwa nyakati mbili tofauti
- tatizo la thamani ya mipaka
- equation tofauti na hali ya mipaka inayohusishwa
- tabia equation
- equation\(aλ^2+bλ+c=0\) kwa equation tofauti\(ay″+by′+cy=0\)
- homogeneous equation
- pili ili tofauti equation ambayo inaweza kuandikwa katika fomu\(a_2(x)y″+a_1(x)y′+a_0(x)y=r(x)\), lakini\(r(x)=0\) kwa kila thamani ya\(x\)
- equation isiyo ya kawaida ya mstari
- pili ili tofauti equation ambayo inaweza kuandikwa katika fomu\(a_2(x)y″+a_1(x)y′+a_0(x)y=r(x)\), lakini\(r(x)≠0\) kwa baadhi ya thamani ya\(x\)
- tegemezi linearly
- seti ya kazi ambazo kuna mara\(f_1(x),\,f_2(x),\,…,\,f_n(x)\) kwa mara\(c_1,\,c_2,\,…,\,c_n\), sio sifuri zote, kama vile\(c_1f_1(x)+c_2f_2(x)+⋯+c_nf_n(x)=0\) kwa wote\(x\) katika kipindi cha riba
- kujitegemea kwa mstari
- seti ya kazi\(f_1(x),\,f_2(x),\,…,\,f_n(x)\) ambayo hakuna constants\(c_1,\,c_2,\,…,\,c_n\), kama kwamba\(c_1f_1(x)+c_2f_2(x)+⋯+c_nf_n(x)=0\) kwa wote\(x\) katika kipindi cha riba


