16.8E: Mazoezi ya Sehemu ya 16.8

Last updated
Save as PDF

Page ID: 178911

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Kwa mazoezi ya 1 - 9, tumia mfumo wa kompyuta ya algebraic (CAS) na theorem ya tofauti ili kutathmini uso muhimu$\displaystyle \int_S \vecs F \cdot \vecs n \, ds$ kwa uchaguzi uliopewa$\vecs F$ na uso wa mipaka$S.$ Kwa kila uso uliofungwa, kudhani$\vecs N$ ni kitengo cha nje cha vector ya kawaida.

1. [T]$\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}$;$S$ ni uso wa mchemraba$0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 < z \leq 1$.

2. [T]$\vecs F(x,y,z) = (\cos yz) \,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + 3z^2 \,\mathbf{\hat k}$;$S$ ni uso wa hemisphere$z = \sqrt{4 - x^2 - y^2}$ pamoja na disk$x^2 + y^2 \leq 4$ katika$xy$ -ndege.

Jibu: $\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 75.3982$

3. [T]$\vecs F(x,y,z) = (x^2 + y^2 - x^2)\,\mathbf{\hat i} + x^2 y\,\mathbf{\hat j} + 3z\,\mathbf{\hat k}; $$S$ ni uso wa nyuso tano za mchemraba kitengo$0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 < z \leq 1.$

4. [T]$\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}; $$S$ ni uso wa paraboloid$z = x^2 + y^2$ kwa$0 \leq z \leq 9$.

Jibu: $\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 127.2345$

5. [T]$\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}$;$S$ ni uso wa nyanja$x^2 + y^2 + z^2 = 4$.

6. [T]$\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + (z^2 - 1)\,\mathbf{\hat k}$;$S$ ni uso wa imara imepakana$ x^2 + y^2 = 4$ na silinda na ndege$z = 0$ na$z = 1$.

Jibu: $\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 37.699$

7. [T]$\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}$;$S$ ni uso umefungwa juu$\rho = 2$ na nyanja na chini na koni$\varphi = \dfrac{\pi}{4}$ katika kuratibu spherical. (Fikiria$S$ kama uso wa “koni ya ice cream.”)

8. [T]$\vecs F(x,y,z) = x^3\,\mathbf{\hat i} + y^3 \,\mathbf{\hat j} + 3a^2z \,\mathbf{\hat k} \, (constant \, a > 0)$;$S$ ni uso imepakana na silinda$x^2 + y^2 = a^2$ na ndege$z = 0$ na$z = 1$.

Jibu: $\displaystyle \int_S \vecs F \cdot \vecs n \, ds = \dfrac{9\pi a^4}{2}$

9. [T] Uso muhimu$\displaystyle \iint_S \vecs F \cdot dS$, ambapo$S$ ni imara imepakana na paraboloid$z = x^2 + y^2$ na ndege$z = 4$, na$\vecs F(x,y,z) = (x + y^2z^2)\,\mathbf{\hat i} + (y + z^2x^2)\,\mathbf{\hat j} + (z + x^2y^2) \,\mathbf{\hat k}$

10. Tumia theorem ya tofauti ili kuhesabu uso muhimu$\displaystyle \iint_S \vecs F \cdot dS$, wapi$\vecs F(x,y,z) = (e^{y^2} \,\mathbf{\hat i} + (y + \sin (z^2))\,\mathbf{\hat j} + (z - 1)\,\mathbf{\hat k}$ na$S$ ni hemphere ya juu$x^2 + y^2 + z^2 = 1, \, z \geq 0$, inaelekezwa juu.

Jibu: $\displaystyle \iint_S \vecs F \cdot dS = \dfrac{\pi}{3}$

11. Matumizi theorem tofauti kwa mahesabu ya uso muhimu$\displaystyle \iint_S \vecs F \cdot dS$, ambapo$\vecs F(x,y,z) = x^4\,\mathbf{\hat i} - x^3z^2\,\mathbf{\hat j} + 4xy^2z\,\mathbf{\hat k}$ na$S$ ni uso imepakana na silinda$x^2 + y^2 = 1$ na ndege$z = x + 2$ na$z = 0$.

12. Tumia theorem ya tofauti ili kuhesabu uso muhimu$\displaystyle \iint_S \vecs F \cdot dS$, wakati$\vecs F(x,y,z) = x^2z^3 \,\mathbf{\hat i} + 2xyz^3\,\mathbf{\hat j} + xz^4 \,\mathbf{\hat k}$ na$S$ ni uso wa sanduku na vipeo$(\pm 1, \, \pm 2, \, \pm 3)$.

Jibu: $\displaystyle \iint_S \vecs F \cdot dS = 0$

13. Matumizi theorem tofauti kwa mahesabu ya uso muhimu$\displaystyle \iint_S \vecs F \cdot dS$, wakati$\vecs F(x,y,z) = z \, \tan^{-1} (y^2)\,\mathbf{\hat i} + z^3 \ln(x^2 + 1) \,\mathbf{\hat j} + z\,\mathbf{\hat k}$ na$S$ ni sehemu ya paraboloid$x^2 + y^2 + z = 2$ kwamba uongo juu ya ndege$z = 1$ na ni oriented zaidi.

14. [T] Matumizi CAS na theorem tofauti kwa mahesabu ya flux$\displaystyle \iint_S \vecs F \cdot dS$, ambapo$\vecs F(x,y,z) = (x^3 + y^3)\,\mathbf{\hat i} + (y^3 + z^3)\,\mathbf{\hat j} + (z^3 + x^3)\,\mathbf{\hat k} $ na$S$ ni nyanja na kituo$(0, 0)$ na Radius$2.$

Jibu: $\displaystyle \iint_S \vecs F \cdot dS = 241.2743$

15. Matumizi theorem tofauti kukokotoa thamani ya flux muhimu$\displaystyle \iint_S \vecs F \cdot dS$, ambapo$\vecs F(x,y,z) = (y^3 + 3x)\,\mathbf{\hat i} + (xz + y)\,\mathbf{\hat j} + \left(z + x^4 \cos (x^2y)\right)\,\mathbf{\hat k}$ na$S$ ni eneo la mkoa imepakana na$x^2 + y^2 = 1, \, x \geq 0, \, y \geq 0$, na$0 \leq z \leq 1$.

0, y>0, and z>0. A quarter of a cylinder is drawn with center on the z axis. The arrows have positive x, y, and z components; they point away from the origin." data-type="media"> Shamba la vector katika vipimo vitatu, kwa kuzingatia eneo hilo na x 0, y> 0, na z> 0. Robo ya silinda hutolewa na kituo cha mhimili z. Mishale ina vipengele vyema vya x, y, na z; huelekeza mbali na asili." src="https://math.libretexts.org/@api/dek...16_08_202.jpeg">

16. Matumizi theorem tofauti kukokotoa flux muhimu$\displaystyle \iint_S \vecs F \cdot dS$, where $\vecs F(x,y,z) = y\,\mathbf{\hat j} - z\,\mathbf{\hat k}$ and $S$ consists of the union of paraboloid $y = x^2 + z^2, \, 0 \leq y \leq 1$, and disk $x^2 + z^2 \leq 1, \, y = 1$, oriented outward. What is the flux through just the paraboloid?

Answer: $\displaystyle \iint_S \vecs F \cdot dS = -\pi$

17. Use the divergence theorem to compute flux integral $\displaystyle \iint_S \vecs F \cdot dS$, where $\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z^4 \,\mathbf{\hat k}$ and $S$ is a part of cone $z = \sqrt{x^2 + y^2}$ beneath top plane $z = 1$ oriented downward.

18. Use the divergence theorem to calculate surface integral $\displaystyle \iint_S \vecs F \cdot dS$ for $\vecs F(x,y,z) = x^4\,\mathbf{\hat i} - x^3z^2\,\mathbf{\hat j} + 4xy^2 z\,\mathbf{\hat k}$, where $S$ is the surface bounded by cylinder $x^2 + y^2 = 1$ and planes $z = x + 2$ and $z = 0$.

Answer: $\displaystyle \iint_S \vecs F \cdot dS = \dfrac{2\pi}{3}$

19. Consider $\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + xy\,\mathbf{\hat j} + (z + 1)\,\mathbf{\hat k}$. Let $E$ be the solid enclosed by paraboloid $z = 4 - x^2 - y^2$ and plane $z = 0$ with normal vectors pointing outside $E.$ Compute flux $\vecs F$ across the boundary of $E$ using the divergence theorem.

In exercises 20 - 23, use a CAS along with the divergence theorem to compute the net outward flux for the fields across the given surfaces $S.$

20. [T] $\vecs F = \langle x,\, -2y, \, 3z \rangle; $ $S$ is sphere $\{(x,y,z) : x^2 + y^2 + z^2 = 6 \}$.

Answer: $15\sqrt{6}\pi$

21. [T] $\vecs F = \langle x, \, 2y, \, z \rangle$; $S$ is the boundary of the tetrahedron in the first octant formed by plane $x + y + z = 1$.

22. [T] $\vecs F = \langle y - 2x, \, x^3 - y, \, y^2 - z \rangle$; $S$ is sphere $\{(x,y,z) \,:\, x^2 + y^2 + z^2 = 4\}.$

Answer: $-\dfrac{128}{3} \pi$

23. [T] $\vecs F = \langle x,y,z \rangle$; $S$ is the surface of paraboloid $z = 4 - x^2 - y^2$, for $z \geq 0$, plus its base in the $xy$-plane.

For exercises 24 - 26, use a CAS and the divergence theorem to compute the net outward flux for the vector fields across the boundary of the given regions $D.$

24. [T] $\vecs F = \langle z - x, \, x - y, \, 2y - z \rangle$; $D$ is the region between spheres of radius 2 and 4 centered at the origin.

Answer: $-703.7168$

25. [T] $\vecs F = \dfrac{\vecs r}{\|\vecs r\|} = \dfrac{\langle x,y,z\rangle}{\sqrt{x^2+y^2+z^2}}$; $D$ is the region between spheres of radius 1 and 2 centered at the origin.

26. [T] $\vecs F = \langle x^2, \, -y^2, \, z^2 \rangle$; $D$ is the region in the first octant between planes $z = 4 - x - y$ and $z = 2 - x - y$.

Answer: $20$

27. Let $\vecs F(x,y,z) = 2x\,\mathbf{\hat i} - 3xy\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}$. Use the divergence theorem to calculate $\displaystyle \iint_S \vecs F \cdot dS$, where $S$ is the surface of the cube with corners at $(0,0,0), \, (1,0,0), \, (0,1,0), \, (1,1,0), \, (0,0,1), \, (1,0,1), \, (0,1,1)$, and $(1,1,1)$, oriented outward.

28. Use the divergence theorem to find the outward flux of field $\vecs F(x,y,z) = (x^3 - 3y)\,\mathbf{\hat i} + (2yz + 1)\,\mathbf{\hat j} + xyz\,\mathbf{\hat k}$ through the cube bounded by planes $x = \pm 1, \, y = \pm 1, $ and $z = \pm 1$.

Answer: $\displaystyle \iint_S \vecs F \cdot dS = 8$

29. Let $\vecs F(x,y,z) = 2x\,\mathbf{\hat i} - 3y\,\mathbf{\hat j} + 5z\,\mathbf{\hat k}$ and let $S$ be hemisphere $z = \sqrt{9 - x^2 - y^2}$ together with disk $x^2 + y^2 \leq 9$ in the $xy$-plane. Use the divergence theorem.

30. Evaluate $\displaystyle \iint_S \vecs F \cdot \vecs n \, dS$, where $\vecs F(x,y,z) = x^2 \,\mathbf{\hat i} + xy\,\mathbf{\hat j} + x^3y^3\,\mathbf{\hat k}$ and $S$ is the surface consisting of all faces except the tetrahedron bounded by plane $x + y + z = 1$ and the coordinate planes, with outward unit normal vector $\vecs N.$

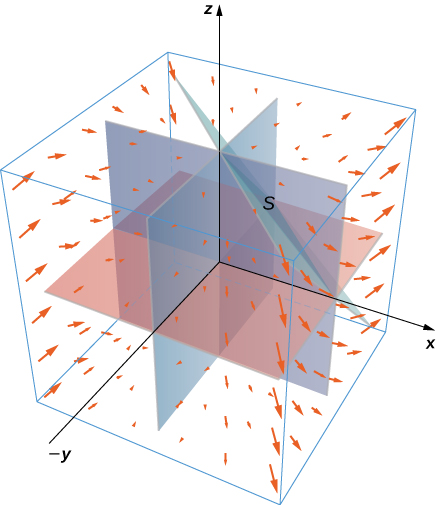
$A vector field in three dimensions, with arrows becoming larger the further away from the origin they are, especially in their x components. S is the surface consisting of all faces except the tetrahedron bounded by the plane x + y + z = 1. As such, a portion of the given plane, the (x, y) plane, the (x, z) plane, and the (y, z) plane are shown. The arrows point towards the origin for negative x components, away from the origin for positive x components, down for positive x and negative y components, as well as positive y and negative x components, and for positive x and y components, as well as negative x and negative y components.$

Jibu: $\displaystyle \iint_S \vecs F \cdot \vecs n \, dS = \dfrac{1}{8}$

31. Kupata wavu nje flux ya shamba$\vecs F = \langle bz - cy, \, cx - az, \, ay - bx \rangle$ katika uso wowote laini kufungwa katika$R^3$ wapi$a, \, b,$ na$c$ ni constants.

32. Tumia theorem ya tofauti ili kutathmini$\displaystyle \iint_S ||\vecs R||\vecs R \cdot \vecs n \, ds,$ wapi$\vecs R(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}$ na$S$ ni nyanja$x^2 + y^2 + z^2 = a^2$, na mara kwa mara$a > 0$.

Jibu: $\displaystyle \iint_S ||\vecs R||\vecs R \cdot \vecs n \, ds = 4\pi a^4$

33. Matumizi theorem tofauti kutathmini$\displaystyle \iint_S \vecs F \cdot dS,$ wapi$\vecs F(x,y,z) = y^2 z\,\mathbf{\hat i} + y^3\,\mathbf{\hat j} + xz\,\mathbf{\hat k}$ na$S$ ni mipaka ya mchemraba inavyoelezwa na$-1 \leq x \leq 1, \, -1 \leq y \leq 1$, na$0 \leq z \leq 2$.

34. Hebu$R$ kuwa kanda inavyoelezwa na$x^2 + y^2 + z^2 \leq 1$. Tumia theorem ya tofauti ili kupata$\displaystyle \iiint_R z^2 \, dV.$

Jibu: $\displaystyle \iiint_R z^2 dV = \dfrac{4\pi}{15}$

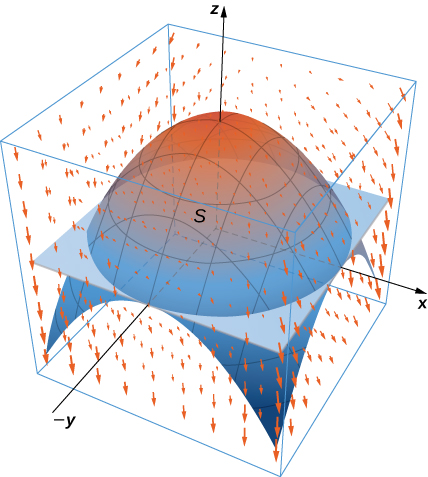
35. Hebu$E$ kuwa imara imepakana na$xy$ -plane na paraboloid$z = 4 - x^2 - y^2$ hivyo kwamba$S$ ni uso wa kipande paraboloid pamoja na disk katika$xy$ -plane ambayo huunda chini yake. Ikiwa$\vecs F(x,y,z) = (xz \, \sin(yz) + x^3) \,\mathbf{\hat i} + \cos (yz) \,\mathbf{\hat j} + (3zy^2 - e^{x^2+y^2})\,\mathbf{\hat k}$, tafuta$\displaystyle \iint_S \vecs F \cdot dS$ kutumia theorem ya tofauti.

$shamba vector katika vipimo tatu na yote ya mishale akizungumzia chini. Wanaonekana kufuata njia ya paraboloidi inayotolewa kufunguliwa chini na kipeo kwenye asili. S ni uso wa paraboloid hii na diski katika ndege (x, y) inayounda chini yake.$

36. Hebu

Template:ContribOpenStaxCalc