13.5: Mazoezi ya Mapitio ya Sura ya 13
- Page ID
- 178337
Kweli au Uongo? Thibitisha jibu lako kwa ushahidi au mfano wa kukabiliana.
1. Equation parametric ambayo hupita kupitia pointi\(P\) na\(Q\) inaweza kutolewa na\(\vecs r(t)=⟨t^2,\, 3t+1,\, t−2⟩,\) wapi\(P(1,4,−1)\) na\(Q(16,11,2).\)
2. \(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=2\vecs u′(t)×\vecs u(t)\)
- Jibu
- Uongo,\(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u(t)\Big]=\vecs 0.\)
3. Curvature ya mduara wa radius\(r\) ni mara kwa mara kila mahali. Aidha, curvature ni sawa na\(1/r.\)
4. Kasi ya chembe yenye kazi ya msimamo\(\vecs r(t)\) ni\(\dfrac{\vecs r′(t)}{\|\vecs r′(t)\|}.\)
- Jibu
- Uongo, ni\(\|\vecs r′(t)\|\)
Pata vikoa vya kazi za thamani ya vector.
5. \(\vecs r(t)=⟨\sin(t),\, \ln(t),\, \sqrt{t}⟩\)
6. \(\vecs r(t)=\left\langle e^t,\,\dfrac{1}{\sqrt{4−t}},\,\sec t\right\rangle\)
- Jibu
- \(t<4, \; t≠\dfrac{nπ}{2}\)
Mchoro curves kwa equations zifuatazo vector. Tumia calculator ikiwa inahitajika.
7. [T]\(\vecs r(t)=⟨t^2,\, t^3⟩\)
8. [T]\(\vecs r(t)=⟨\sin(20t)e^{−t}, \, \cos(20t)e^{−t}, \, e^{−t}⟩\)
- Jibu
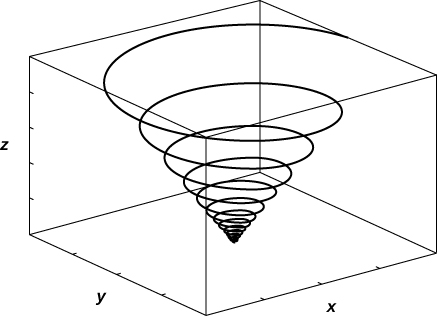
Kupata kazi vector kwamba inaelezea curves zifuatazo.
9. Makutano ya silinda\(x^2+y^2=4\) na ndege\(x+z=6\)
10. Makutano ya koni\(z=\sqrt{x^2+y^2}\) na ndege\(z=y−4\)
- Jibu
- \(\vecs r(t)=\left\langle t, \, 2-\frac{t^2}{8},\, -2 - \frac{t^2}{8}\right\rangle\)
Kupata derivatives ya\(\vecs u(t), \, \vecs u′(t), \, \vecs u′(t)×\vecs u(t), \, \vecs u(t)×\vecs u′(t),\) na\(\vecs u(t)·\vecs u′(t).\) Kupata kitengo tangent vector.
11. \(\vecs u(t)=⟨e^t, \, e^{−t}⟩\)
12. \(\vecs u(t)=⟨t^2,\, 2t+6, \, 4t^5−12⟩\)
- Jibu
- \(\vecs u′(t)=⟨2t, \, 2, \, 20t^4⟩,\)
\(\vecs u″(t)=⟨2, \, 0, \, 80t^3⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u′(t)×\vecs u(t)\Big]=⟨−480t^3−160t^4, \, 24+75t^2, \, 12+4t⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u(t)×\vecs u′(t)\Big]=⟨480t^3+160t^4, \, -24-75t^2, \, -12-4t⟩,\)
\(\dfrac{d}{dt}\Big[\vecs u(t)⋅\vecs u′(t)\Big]=720t^8−9600t^3+6t^2+4,\)
kitengo tangent vector:\(\vecs T(t)=\dfrac{2t}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat i}+\dfrac{2}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat j}+\dfrac{20t^4}{\sqrt{400t^8+4t^2+4}}\,\mathbf{\hat k}\)
Tathmini integrals zifuatazo.
13. \(\displaystyle ∫\left(\tan(t)\sec(t)\,\mathbf{\hat i}−te^{3t}\,\mathbf{\hat j}\right)\, dt\)
14. \(\displaystyle ∫_1^4 \vecs u(t) \, dt,\)na\(\vecs u(t)=\left\langle\dfrac{\ln t}{t}, \, \dfrac{1}{\sqrt{t}}, \, \sin\left(\frac{tπ}{4}\right)\right\rangle\)
- Jibu
- \(\dfrac{\ln(4^2)}{2}\,\mathbf{\hat i}+2\,\mathbf{\hat j}+\dfrac{2(2+\sqrt{2})}{\pi}\,\mathbf{\hat k}\)
Kupata urefu kwa curves zifuatazo.
15. \(\vecs r(t)=⟨3t,\, 4\cos t, \, 4\sin t ⟩\)kwa\(1≤t≤4\)
16. \(\vecs r(t)=2\,\mathbf{\hat i}+t\,\mathbf{\hat j}+3t^2\,\mathbf{\hat k}\)kwa\(0≤t≤1\)
- Jibu
- \(\dfrac{\sqrt{37}}{2}+\frac{1}{12}\sinh^{−1} 6\)
Repameterize kazi zifuatazo kwa heshima ya urefu wao wa arc kipimo kutoka\(t=0\) kwa uongozi wa kuongezeka\(t.\)
17. \(\vecs r(t)=2t\,\mathbf{\hat i}+(4t−5)\,\mathbf{\hat j}+(1−3t)\,\mathbf{\hat k}\)
18. \(\vecs r(t)=\cos(2t)\,\mathbf{\hat i}+8t\,\mathbf{\hat j}−\sin(2t)\,\mathbf{\hat k}\)
- Jibu
- \(\vecs r(t(s))=\cos\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat i}+\frac{8s}{\sqrt{65}}\,\mathbf{\hat j}−\sin\left(\frac{2s}{\sqrt{65}}\right)\,\mathbf{\hat k}\)
Kupata curvature kwa ajili ya kazi zifuatazo vector.
19. \(\vecs r(t)=(2\sin t)\,\mathbf{\hat i}−4t\,\mathbf{\hat j}+(2\cos t)\,\mathbf{\hat k}\)
20. \(\vecs r(t)=\sqrt{2}e^t\,\mathbf{\hat i}+\sqrt{2}e^{−t}\,\mathbf{\hat j}+2t\,\mathbf{\hat k}\)
- Jibu
- \(\dfrac{e^{2t}}{\left(e^{2t}+1\right)^2}\)
21. Kupata kitengo tangent vector, kitengo kawaida vector, na vector binormal kwa\(\vecs r(t)=2\cos t\,\mathbf{\hat i} +3t\,\mathbf{\hat j}+2sint\,\mathbf{\hat k}.\)
22. Kupata tangential na ya kawaida kuongeza kasi vipengele na nafasi vector\(\vecs r(t)=⟨\cos t,\, \sin t, \, e^t⟩.\)
- Jibu
- \(a_T=\dfrac{e^{2t}}{1+e^{2t}},\)
\(a_N=\dfrac{\sqrt{2e^{2t}+4e^{2t}\sin t\cos t+1}}{1+e^{2t}}\)
23. Gari la gurudumu la Ferris linasonga kwa kasi ya mara kwa mara\(v\) na ina radius ya mara kwa mara\(r.\) Pata kasi ya kasi na ya kawaida ya gari la gurudumu la Ferris.
24. Msimamo wa chembe hutolewa na\(\vecs r(t)=⟨t^2, \, \ln t, \, \sin(πt)⟩,\) wapi\(t\) hupimwa kwa sekunde na\(r\) hupimwa kwa mita. Kupata kasi, kuongeza kasi, na kasi ya kazi. Je! Ni nafasi gani, kasi, kasi, na kasi ya chembe saa 1 sec?
- Jibu
- \(\vecs v(t)=\left\langle 2t,\, \frac{1}{t}, \, \pi\cos(πt)\right\rangle\text{ m/sec},\)
\(\vecs a(t)=\left\langle 2, \, −\frac{1}{t^2}, \, −\pi^2\sin(πt) \right\rangle\text{ m/sec}^2,\)
\(\text{speed}(t)=\sqrt{4t^2+\frac{1}{t^2}+\pi^2\cos^2(πt)}\text{ m/sec}\);
Katika\(t=1,\; \vecs r(1)=⟨1,0,0⟩\) m,\(\vecs v(1)=⟨2,−1,\pi⟩\) m/sec,\(\vecs a(1)=⟨2,−1,0⟩\) m/sec 2, na\(\text{speed}(1) =\sqrt{5+\pi^2}\) m/sec
Matatizo yafuatayo yanazingatia uzinduzi wa cannonball nje ya kanuni. Cannonball hupigwa nje ya kanuni kwa kasi na kasi ya\(θ\) awali. nguvu pekee\(\vecs v_0.\) inayofanya cannonball ni mvuto, hivyo tunaanza na kasi ya mara kwa mara\(\vecs a(t)=−g\,\mathbf{\hat j}.\)
25. Pata kazi ya vector kasi\(\vecs v(t).\)
26. Pata vector msimamo\(\vecs r(t)\) na uwakilishi wa parametric kwa nafasi.
- Jibu
- \(\vecs r(t)=\vecs v_0t−\dfrac{gt^2}{2}\,\mathbf{\hat j},\)
\(\vecs r(t)=⟨v_0(\cos θ)t,\,v_0(\sin θ)t,−\dfrac{gt^2}{2}⟩\)wapi\(v_0 = \|\vecs v_0\|.\)
27. Kwa pembe gani unahitaji moto wa cannonball kwa umbali usio na usawa kuwa mkubwa zaidi? ni umbali wa jumla ingekuwa kusafiri nini?


