12.7: Cylindrical na Spherical Kuratibu

Last updated
Save as PDF

Page ID: 178084

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Badilisha kutoka cylindrical hadi kuratibu mstatili
Badilisha kutoka kwa mstatili hadi kuratibu za cylind
Badilisha kutoka kwa spherical hadi kuratibu mstatili.
Badilisha kutoka mstatili hadi kuratibu za spherical.

Mfumo wa kuratibu wa Cartesian hutoa njia moja kwa moja ya kuelezea eneo la pointi katika nafasi. Baadhi ya nyuso, hata hivyo, inaweza kuwa vigumu kuiga na equations kulingana na mfumo wa Cartesian. Hili ni tatizo la kawaida; kukumbuka kuwa katika vipimo viwili, kuratibu polar mara nyingi hutoa mfumo mbadala muhimu wa kuelezea eneo la uhakika katika ndege, hasa katika kesi zinazohusisha miduara. Katika sehemu hii, tunaangalia njia mbili tofauti za kuelezea eneo la pointi katika nafasi, zote mbili kulingana na upanuzi wa kuratibu za polar. Kama jina linavyoonyesha, kuratibu za cylindrical ni muhimu kwa kushughulika na matatizo yanayohusisha mitungi, kama vile kuhesabu kiasi cha tank ya maji ya pande zote au kiasi cha mafuta kinachozunguka kupitia bomba. Vile vile, kuratibu za spherical ni muhimu kwa kushughulika na matatizo yanayohusisha nyanja, kama vile kutafuta kiasi cha miundo ya domed.

Kuratibu za Cylind

Tulipopanua mfumo wa kuratibu wa jadi wa Cartesian kutoka vipimo viwili hadi tatu, tuliongeza tu mhimili mpya ili kuiga mwelekeo wa tatu. Kuanzia na kuratibu za polar, tunaweza kufuata mchakato huu huo ili kuunda mfumo mpya wa kuratibu tatu-dimensional, unaoitwa mfumo wa kuratibu cylindrical. Kwa njia hii, kuratibu za cylindrical hutoa ugani wa asili wa kuratibu polar kwa vipimo vitatu.

Ufafanuzi: Mfumo wa Kuratibu wa Cylind

Katika mfumo wa kuratibu wa cylindrical, hatua katika nafasi (Kielelezo$\PageIndex{1}$) inawakilishwa na mara tatu iliyoamriwa$(r,θ,z)$, wapi

$(r,θ)$ni kuratibu polar ya makadirio ya uhakika katika$xy$ -ndege
$z$ni kawaida$z$ - kuratibu katika mfumo wa kuratibu Cartesian

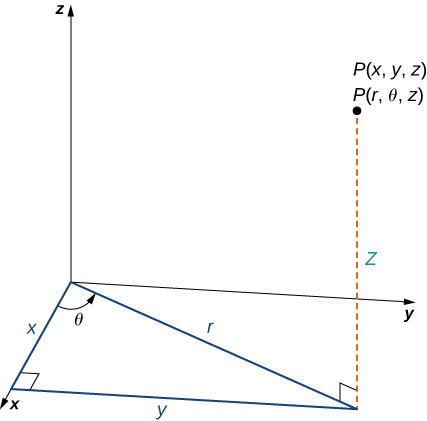
Takwimu hii ni octant ya kwanza ya mfumo wa kuratibu 3-dimensional. Kuna hatua iliyoandikwa “(x, y, z) = (r, theta, z).” Katika x y-ndege, kuna sehemu ya mstari inayoenea hadi chini ya hatua. Sehemu hii ya mstari imeandikwa “r.” Pembe kati ya sehemu ya mstari na x-axis ni theta. Kuna sehemu ya mstari perpendicular kwa x-axis. Pamoja na mstari sehemu kinachoitwa r, hii sehemu line na x-mhimili kuunda pembetatu haki. — Kielelezo$\PageIndex{1}$: Pembetatu ya kulia iko katika$xy$ -ndege. Urefu wa hypotenuse ni$r$ na$θ$ ni kipimo cha angle iliyoundwa na chanya$x$ -axis na hypotenuse. $z$Kuratibu inaelezea eneo la uhakika hapo juu au chini ya$xy$ -ndege.

Katika$xy$ -ndege, pembetatu sahihi inavyoonekana katika Kielelezo$\PageIndex{1}$ hutoa ufunguo wa mabadiliko kati ya cylindrical na Cartesian, au mstatili, kuratibu.

Uongofu kati ya Kuratibu za Cylindrical na Cart

Kuratibu mstatili$(x,y,z)$ na kuratibu cylindrical$(r,θ,z)$ ya uhakika ni kuhusiana kama ifuatavyo:

Equations hizi hutumiwa kubadili kutoka kuratibu za cylindrical hadi kuratibu mstatili.

$x=r\cos θ$
$y=r\sin θ$
$z=z$

Equations hizi hutumiwa kubadili kutoka kuratibu mstatili hadi kuratibu za cylindrical

$r^2=x^2+y^2$
$\tan θ=\dfrac{y}{x}$
$z=z$

Kama tulipojadili uongofu kutoka kwa kuratibu za mstatili hadi kuratibu za polar katika vipimo viwili, ni lazima ieleweke kwamba equation$\tan θ=\dfrac{y}{x}$ ina idadi isiyo na kipimo cha ufumbuzi. Hata hivyo, ikiwa tunazuia$θ$ maadili kati$0$ na$2π$, basi tunaweza kupata suluhisho la kipekee kulingana na quadrant ya $xy$-plane ambayo hatua ya awali$(x,y,z)$ iko. Kumbuka kwamba kama$x=0$, basi thamani ya$θ$ ni ama$\dfrac{π}{2},\dfrac{3π}{2},$ au$0$, kulingana na thamani ya$y$.

Angalia kwamba equations hizi zinatokana na mali ya pembetatu sahihi. Ili kufanya hili rahisi kuona, fikiria uhakika$P$ katika $xy$-ndege na kuratibu mstatili$(x,y,0)$ na kuratibu cylindrical$(r,θ,0)$, kama inavyoonekana katika Kielelezo$\PageIndex{2}$.

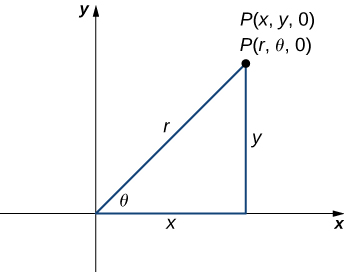
Takwimu hii ni quadrant ya kwanza ya mfumo wa kuratibu mstatili. Kuna hatua iliyoandikwa “P = (x, y, 0) = (r, theta, 0).” Kuna sehemu ya mstari kutoka asili hadi kumweka P. sehemu hii ya mstari inaitwa “r.” Pembe kati ya mhimili wa x na sehemu ya mstari r inaitwa “theta.” Pia kuna sehemu ya mstari wa wima iliyoitwa “y” kutoka P hadi mhimili wa x. Inaunda pembetatu sahihi. — Kielelezo$\PageIndex{2}$: Theorem ya Pythagorean hutoa equation$r^2=x^2+y^2$. Mahusiano ya pembetatu ya kulia yanatuambia kwamba$x=r\cos θ, y=r\sin θ,$ na$\tan θ=y/x.$

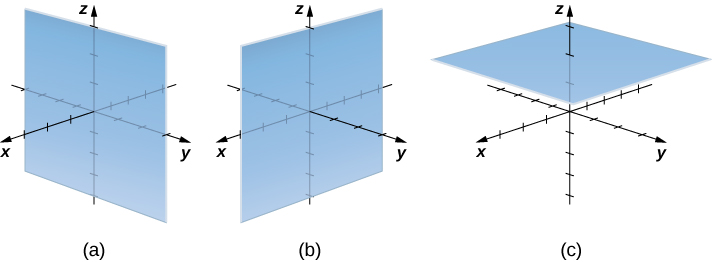
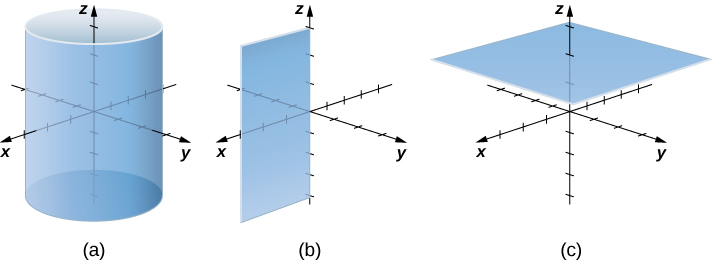
Hebu fikiria tofauti kati ya kuratibu mstatili na cylindrical kwa kuangalia nyuso zinazozalishwa wakati kila kuratibu inafanyika mara kwa mara. Ikiwa$c$ ni mara kwa mara, basi katika kuratibu mstatili, nyuso za fomu$x=c, y=c,$ au$z=c$ ni ndege zote. Ndege za fomu hizi ni sawa na$yz$ -ndege,$xz$ -ndege, na$xy$ -ndege, kwa mtiririko huo. Tunapobadilisha kwa kuratibu za cylindrical,$z$ -kuratibu haibadilika. Kwa hiyo, katika kuratibu za cylindrical, nyuso za fomu$z=c$ ni ndege zinazofanana na$xy$ -ndege. Sasa, hebu fikiria juu ya nyuso za fomu$r=c$. Pointi juu ya nyuso hizi ni umbali wa kudumu kutoka$z$ -axis. Kwa maneno mengine, nyuso hizi ni mitungi ya mviringo ya wima. Mwisho, vipi$θ=c$? Pointi juu ya uso wa fomu$θ=c$ ni kwenye pembe ya kudumu kutoka$x$ -axis, ambayo inatupa nusu ya ndege inayoanza saa$z$ -axis (Takwimu$\PageIndex{3}$ na$\PageIndex{4}$).

Takwimu hii ina picha 3. Picha ya kwanza ni ndege katika mfumo wa kuratibu 3-dimensional. Ni sambamba na y z-ndege ambapo x = c. picha ya pili ni ndege katika 3-dimensional kuratibu mfumo. Ni sambamba na x z-ndege ambapo y = c. picha ya tatu ni ndege katika mfumo wa kuratibu 3-dimensional ambapo z = c. — Kielelezo$\PageIndex{3}$: Katika kuratibu mstatili, (a) nyuso za fomu$x=c$ ni$yz$ ndege zinazofanana na ndege, (b) nyuso za fomu$y=c$ ni ndege$xz$ zinazofanana na ndege, na (c) nyuso za fomu$z=c$ ni ndege zinazofanana na$xy$ ndege.

Takwimu hii ina picha 3. Picha ya kwanza ni silinda ya mviringo sahihi katika mfumo wa kuratibu 3-dimensional. Ina mhimili wa z katikati. Picha ya pili ni ndege katika mfumo wa kuratibu 3-dimensional. Ni wima na mhimili wa z kwenye makali moja. Picha ya tatu ni ndege katika mfumo wa kuratibu 3-dimensional ambapo z = c. — Kielelezo$\PageIndex{4}$: Katika kuratibu cylindrical, (a) nyuso za fomu$r=c$ ni mitungi ya wima ya radius$r$, (b) nyuso za fomu$θ=c$ ni ndege za nusu kwa pembe$θ$ kutoka$x$ -axis, na (c) nyuso za fomu$z=c$ ni ndege zinazofanana na$xy$ - ndege.

Mfano$\PageIndex{1}$: Converting from Cylindrical to Rectangular Coordinates

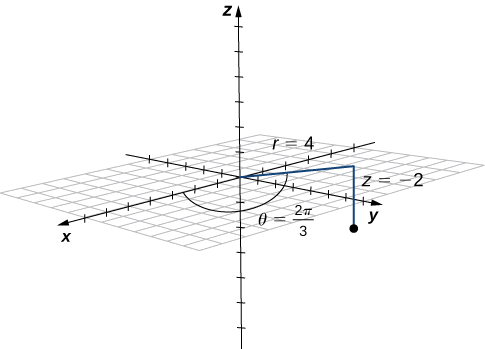
Panda hatua na kuratibu za cylindrical$(4,\dfrac{2π}{3},−2)$ na ueleze eneo lake katika kuratibu za mstatili.

Suluhisho

Uongofu kutoka kwa cylindrical hadi kuratibu mstatili inahitaji matumizi rahisi ya equations iliyoorodheshwa katika Kumbuka:

\[\begin{align*} x &=r\cos θ=4\cos\dfrac{2π}{3}=−2 \\[4pt] y &=r\sin θ=4\sin \dfrac{2π}{3}=2\sqrt{3} \\[4pt] z &=−2 \end{align*}. \nonumber \]

Hatua na kuratibu za cylindrical$(4,\dfrac{2π}{3},−2)$ ina kuratibu mstatili$(−2,2\sqrt{3},−2)$ (Kielelezo$\PageIndex{5}$).

Takwimu hii ni mfumo wa kuratibu wa 3-dimensional. Ina uhakika ambapo r = 4, z = -2 na theta = 2 pi /3. — Kielelezo$\PageIndex{5}$: Makadirio ya uhakika katika$xy$ -ndege ni vitengo 4 kutoka asili. Mstari kutoka kwa asili hadi makadirio ya uhakika huunda angle ya$\dfrac{2π}{3}$ na chanya$x$ -axis. uhakika uongo$2$ vitengo chini$xy$ -ndege.

Zoezi$\PageIndex{1}$

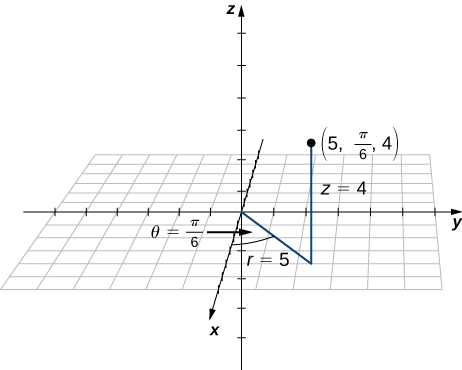
Point$R$ ina kuratibu cylindrical$(5,\frac{π}{6},4)$. Panda$R$ na kuelezea eneo lake katika nafasi kwa kutumia mstatili, au Cartesian, kuratibu.

Kidokezo

Vipengele viwili vya kwanza vinafanana na kuratibu za polar za uhakika katika $xy$-ndege.

Jibu

Kuratibu mstatili wa uhakika ni$(\frac{5\sqrt{3}}{2},\frac{5}{2},4).$

$Takwimu hii ni mfumo wa kuratibu wa 3-dimensional. Kuna hatua iliyoandikwa “(5, pi/6, 4).” Hatua iko juu ya sehemu ya mstari katika x y-ndege iliyoandikwa r = 5 yaani pi/6 digrii kutoka x-axis. Umbali kutoka kwa ndege ya x y hadi hatua ni kinachoitwa “z = 4.”$

Ikiwa mchakato huu unaonekana ukoo, ni kwa sababu nzuri. Hii ni hasa mchakato huo kwamba sisi ikifuatiwa katika Utangulizi wa Parametric Equations na Polar Kuratibu kubadili kutoka kuratibu polar kwa pande mbili kuratibu mstatili.

Mfano$\PageIndex{2}$: Converting from Rectangular to Cylindrical Coordinates

Badilisha kuratibu mstatili$(1,−3,5)$ kwa kuratibu za cylindrical

Suluhisho

Tumia seti ya pili ya equations kutoka Kumbuka ili kutafsiri kutoka kwa mstatili hadi kuratibu za cylindrical:

\[\begin{align*} r^2 &= x^2+y^2 \\[4pt] r &=±\sqrt{1^2+(−3)^2} \\[4pt] &= ±\sqrt{10}. \end{align*}\]

Tunachagua mizizi nzuri ya mraba, kwa$r=\sqrt{10}$ hivyo.Sasa, tunatumia fomu ya kupata$θ$. Katika hali hii,$y$ ni hasi na$x$ ni chanya, ambayo ina maana ni lazima kuchagua thamani ya$θ$ kati$\dfrac{3π}{2}$ na$2π$:

\[\begin{align*} \tan θ &=\dfrac{y}{x} &=\dfrac{−3}{1} \\[4pt] θ &=\arctan(−3) &≈5.03\,\text{rad.} \end{align*}\]

Katika kesi hii, z -kuratibu ni sawa katika kuratibu zote za mstatili na cylindrical:

\[ z=5. \nonumber \]

Hatua na kuratibu mstatili$(1,−3,5)$ ina kuratibu cylindrical takriban sawa na$(\sqrt{10},5.03,5).$

Zoezi$\PageIndex{2}$

Badilisha hatua$(−8,8,−7)$ kutoka kuratibu za Cartesian hadi kuratibu za cylindrical.

Kidokezo: $r^2=x^2+y^2$na$\tan θ=\frac{y}{x}$
Jibu: $(8\sqrt{2},\frac{3π}{4},−7)$

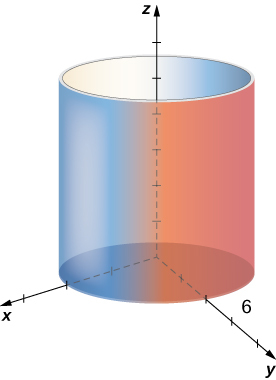
Matumizi ya kuratibu cylindrical ni ya kawaida katika nyanja kama vile fizikia. Wafizikia wanaojifunza mashtaka ya umeme na capacitors waliotumiwa kuhifadhi mashtaka haya wamegundua kwamba mifumo hii wakati mwingine ina ulinganifu wa cylindrical. Mifumo hii ina usawa wa kuimarisha ngumu katika mfumo wa kuratibu wa Cartesian, ambayo huwafanya kuwa vigumu kuelezea na kuchambua. Ulinganisho unaweza mara nyingi kuonyeshwa kwa maneno rahisi zaidi kwa kutumia kuratibu za cylindrical. Kwa mfano, silinda iliyoelezwa na equation$x^2+y^2=25$ katika mfumo wa Cartesian inaweza kuwakilishwa na equation cylindrical$r=5$.

Mfano$\PageIndex{3}$: Identifying Surfaces in the Cylindrical Coordinate System

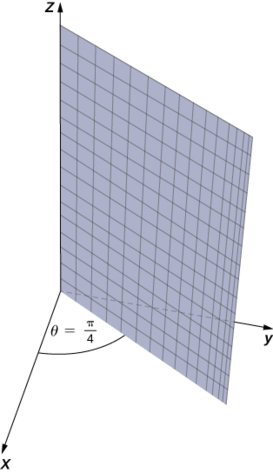
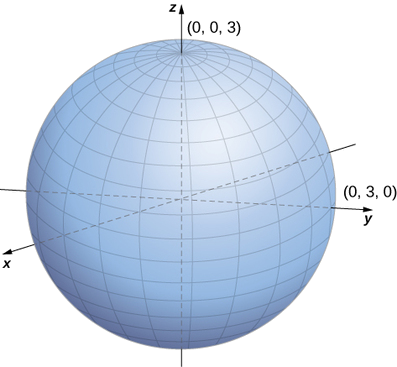
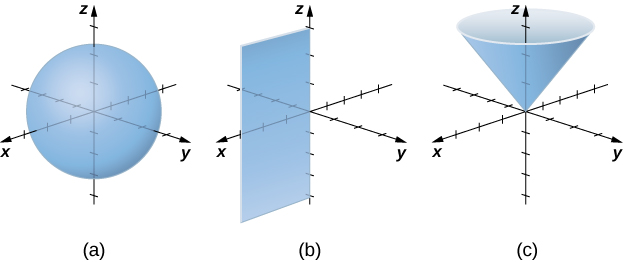
Eleza nyuso na equations zilizopewa cylindrical.

$θ=\dfrac{π}{4}$
$r^2+z^2=9$
$z=r$

Suluhisho

a Wakati angle$θ$ inafanyika mara kwa mara wakati$r$ na$z$ inaruhusiwa kutofautiana, matokeo ni nusu ya ndege (Kielelezo$\PageIndex{6}$).

Takwimu hii ni quadrant ya kwanza ya mfumo wa kuratibu 3-dimensional. Kuna ndege iliyounganishwa na mhimili wa z, kugawanya ndege ya x y na mstari wa diagonal. Pembe kati ya x-axis na ndege hii ni pi/4. — Kielelezo$\PageIndex{6}$: Katika kuratibu polar, equation$θ=π/4$ inaelezea ray kupanua diagonally kupitia roboduara ya kwanza. Katika vipimo vitatu, equation hiyo inaelezea nusu ya ndege.

b Mbadala$r^2=x^2+y^2$ katika equation$r^2+z^2=9$ kueleza fomu mstatili wa equation:$x^2+y^2+z^2=9$. Equation hii inaelezea nyanja unaozingatia katika asili na radius 3 (Kielelezo$\PageIndex{7}$).

Takwimu hii ni nyanja. Ina mhimili wa z kupitia kituo cha wima. Hatua ya makutano na mhimili wa z na nyanja ni (0, 0, 3). Kuna pia mhimili wa y kupitia katikati ya nyanja kwa usawa. Mfululizo wa nyanja na y-axis ni hatua (0, 3, 0). — Kielelezo$\PageIndex{7}$: nyanja iliyozingatia asili na radius 3 inaweza kuelezewa na equation ya cylindrical$r^2+z^2=9$.

c. kuelezea uso inavyoelezwa na equation$z=r$, ni muhimu kuchunguza athari sambamba na$xy$ -ndege. Kwa mfano, mwelekeo wa ndege$z=1$ ni mduara$r=1$, mwelekeo wa ndege$z=3$ ni mduara$r=3$, na kadhalika. Kila mwelekeo ni mduara. Kama thamani ya$z$ ongezeko, radius ya mduara pia huongezeka. Uso unaosababishwa ni koni (Kielelezo$\PageIndex{8}$).

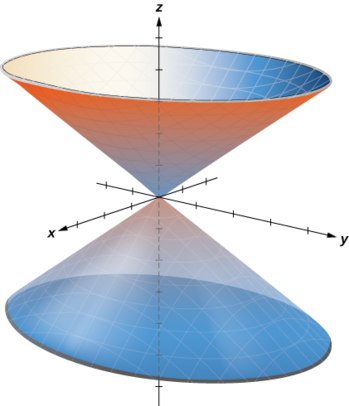
Takwimu hii ni mfumo wa kuratibu wa 3-dimensional. Ina koni ya elliptic na mhimili wa z chini katikati. Vipande viwili, upande mmoja wa kulia juu, mwingine hupungua, hukutana na asili. — Kielelezo$\PageIndex{8}$: Athari katika ndege sambamba na$xy$ -ndege ni duru. Radi ya miduara huongezeka kama$z$ ongezeko.

Zoezi$\PageIndex{3}$

Eleza uso na equation cylindrical$r=6$.

Kidokezo

Ya$θ$ na$z$ vipengele vya pointi juu ya uso vinaweza kuchukua thamani yoyote.

Jibu

Uso huu ni silinda na radius$6$.

$Takwimu hii ni silinda ya mviringo sahihi. Ni sawa na mhimili wa z kupitia katikati. Ni juu ya ndege x y.$

Kuratibu za Spherical

Katika mfumo wa kuratibu wa Cartesian, eneo la uhakika katika nafasi linaelezewa kwa kutumia mara tatu iliyoagizwa ambayo kila kuratibu inawakilisha umbali. Katika mfumo wa kuratibu wa cylindrical, eneo la uhakika katika nafasi linaelezewa kwa kutumia umbali mbili$(r$$z)$ na kipimo cha angle$(θ)$. Katika mfumo wa kuratibu spherical, sisi tena kutumia amri tatu kuelezea eneo la uhakika katika nafasi. Katika kesi hii, mara tatu inaelezea umbali mmoja na pembe mbili. Kuratibu za spherical hufanya iwe rahisi kuelezea nyanja, kama vile kuratibu za cylindrical hufanya iwe rahisi kuelezea silinda. Mstari wa gridi ya kuratibu spherical hutegemea hatua za angle, kama zile za kuratibu polar.

Ufafanuzi: mfumo wa kuratibu spherical

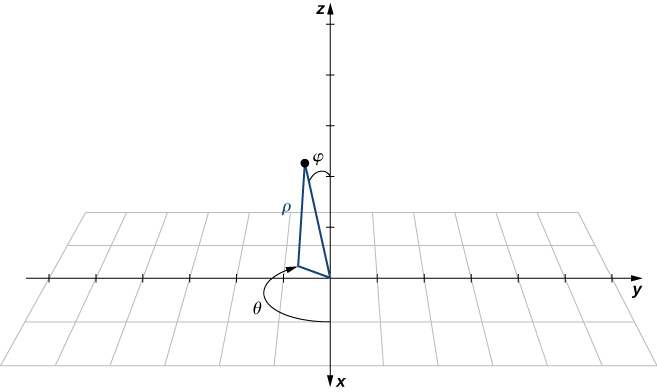
Katika mfumo wa kuratibu wa spherical, hatua$P$ katika nafasi (Kielelezo$\PageIndex{9}$) inawakilishwa na mara tatu iliyoamriwa$(ρ,θ,φ)$ ambapo

$ρ$(barua ya Kigiriki rho) ni umbali kati$P$ na asili$(ρ≠0);$
$θ$ni angle sawa kutumika kuelezea eneo katika kuratibu cylindrical;
$φ$(barua ya Kigiriki phi) ni angle iliyoundwa na sehemu nzuri ya$z$ mhimili na mstari$\bar{OP}$, ambapo$O$ ni asili na$0≤φ≤π.$

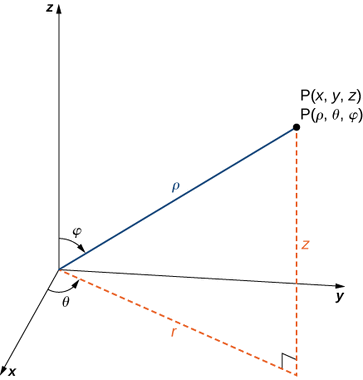
Takwimu hii ni quadrant ya kwanza ya mfumo wa kuratibu 3-dimensional. Ina hatua iliyoandikwa “(x, y, z) = (rho, theta, phi).” Kuna sehemu ya mstari kutoka kwa asili hadi hatua. Ni kinachoitwa “rho.” Pembe kati ya sehemu hii ya mstari na mhimili wa z ni phi. Kuna sehemu ya mstari katika ndege ya x y kutoka asili hadi kivuli cha uhakika. Sehemu hii inaitwa “r.” Pembe kati ya x-axis na r ni theta. — Kielelezo$\PageIndex{9}$: Uhusiano kati ya kuratibu za mviringo, mstatili, na cylindrical.

Kwa mkataba, asili inawakilishwa kama$(0,0,0)$ katika kuratibu za spherical.

HOWTO: Kubadilisha kati ya Mipangilio ya mviringo, ya Cylindrical, na

Kuratibu za mviringo$(x,y,z)$, kuratibu za cylindrical$(r,θ,z),$ na kuratibu spherical$(ρ,θ,φ)$ ya uhakika ni kuhusiana kama ifuatavyo:

Badilisha kutoka viwianishi vya spherical hadi kuratibu

Equations hizi hutumiwa kubadili kutoka kuratibu za spherical hadi kuratibu mstatili.

$x=ρ\sin φ\cos θ$
$y=ρ\sin φ\sin θ$
$z=ρ\cos φ$

Badilisha kutoka viwianishi vya mstatili hadi kuratibu

Equations hizi hutumiwa kubadili kutoka kuratibu mstatili hadi kuratibu za spherical.

$ρ^2=x^2+y^2+z^2$
$\tan θ=\dfrac{y}{x}$
$φ=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}}).$

Badilisha kutoka viwianishi vya spherical hadi kuratibu

Equations hizi hutumiwa kubadili kutoka kuratibu za spherical hadi kuratibu za cylindrical.

$r=ρ\sin φ$
$θ=θ$
$z=ρ\cos φ$

Badilisha kutoka kuratibu za cylindrical hadi kuratibu

Equations hizi hutumiwa kubadili kutoka kuratibu za cylindrical hadi kuratibu za spherical.

$ρ=\sqrt{r^2+z^2}$
$θ=θ$
$φ=\arccos(\dfrac{z}{\sqrt{r^2+z^2}})$

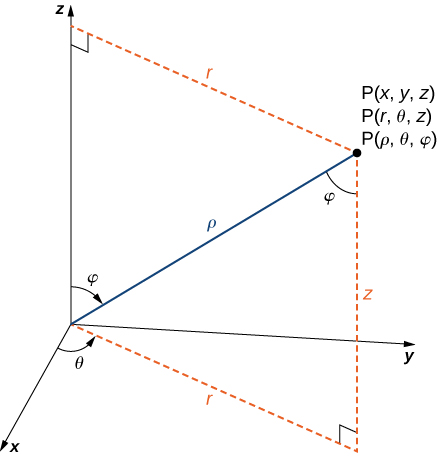
Njia za kubadili kutoka kwa kuratibu za spherical hadi kuratibu za mstatili zinaweza kuonekana kuwa ngumu, lakini ni maombi ya moja kwa moja ya trigonometry. Kuangalia Kielelezo, ni rahisi kuona kwamba$r=ρ \sin φ$. Kisha, kuangalia pembetatu katika$xy$ -plane na r kama hypotenuse yake, tuna$x=r\cos θ=ρ\sin φ \cos θ$. Kupatikana kwa formula kwa$y$ ni sawa. Kielelezo pia inaonyesha kwamba$ρ^2=r^2+z^2=x^2+y^2+z^2$ na$z=ρ\cos φ$. Kutatua equation hii ya mwisho kwa$φ$ na kisha kubadilisha$ρ=\sqrt{r^2+z^2}$ (kutoka equation kwanza) mavuno$φ=\arccos(\dfrac{z}{\sqrt{r^2+z^2}})$. Pia, kumbuka kuwa, kama hapo awali, ni lazima kuwa makini wakati wa kutumia formula ya$\tan θ=\dfrac{y}{x}$ kuchagua thamani sahihi ya$θ$.

Takwimu hii ni quadrant ya kwanza ya mfumo wa kuratibu 3-dimensional. Ina alama iliyoandikwa “(x, y, z) = (r, theta, z) = (rho, theta, phi).” Kuna sehemu ya mstari kutoka kwa asili hadi hatua. Ni kinachoitwa “rho.” Pembe kati ya sehemu hii ya mstari na mhimili wa z ni phi. Kuna sehemu ya mstari katika ndege ya x y kutoka asili hadi kivuli cha uhakika. Sehemu hii inaitwa “r.” Pembe kati ya x-axis na r ni theta.Umbali kutoka r hadi hatua ni kinachoitwa “z.” — Kielelezo$\PageIndex{10}$: Ulinganisho unaobadilisha kutoka mfumo mmoja hadi mwingine unatokana na mahusiano ya pembetatu ya kulia.

Kama tulivyofanya na kuratibu za cylindrical, hebu tuchunguze nyuso zinazozalishwa wakati kila kuratibu hufanyika mara kwa mara. Hebu$c$ kuwa mara kwa mara, na fikiria nyuso za fomu$ρ=c$. Pointi juu ya nyuso hizi ni umbali wa kudumu kutoka kwa asili na huunda nyanja. Kuratibu$θ$ katika mfumo wa kuratibu wa spherical ni sawa na katika mfumo wa kuratibu wa cylindrical, hivyo nyuso za fomu$θ=c$ ni ndege za nusu, kama hapo awali. Mwisho, fikiria nyuso za fomu$φ=0$. Pointi juu ya nyuso hizi ni kwenye angle fasta kutoka$z$ -axis na kuunda nusu koni (Kielelezo$\PageIndex{11}$).

Takwimu hii ina picha tatu. Picha ya kwanza ni nyanja iliyozingatia mfumo wa kuratibu wa 3-dimensional. Takwimu ya pili ni ndege ya wima yenye makali kwenye mhimili wa z katika mfumo wa kuratibu 3-dimensional. Picha ya tatu ni koni ya elliptical na katikati ya asili ya mfumo wa kuratibu 3-dimensional. — Kielelezo$\PageIndex{11}$: Katika viwianishi vya mviringo, nyuso za fomu$ρ=c$ ni nyanja za radius$ρ$ (a), nyuso za fomu$θ=c$ ni ndege za nusu kwa pembe$θ$ kutoka$x$ -axis (b), na nyuso za fomu$ϕ=c$ ni mbegu za nusu kwa pembe$ϕ$ kutoka $z$-mhimili (c).

Mfano$\PageIndex{4}$: Converting from Spherical Coordinates

Panda hatua na kuratibu za spherical$(8,\dfrac{π}{3},\dfrac{π}{6})$ na ueleze eneo lake katika kuratibu zote za mstatili na za cylindrical

Suluhisho

Tumia equations katika Kumbuka kutafsiri kati ya kuratibu spherical na cylindrical (Kielelezo$\PageIndex{12}$):

\[ \begin{align*} x &=ρ\sin φ\cos θ \\[4pt] &=8 \sin(\dfrac{π}{6}) \cos(\dfrac{π}{3}) \\[4pt] &= 8(\dfrac{1}{2})\dfrac{1}{2} \\[4pt] &=2 \\[4pt] y &=ρ\sin φ\sin θ \\[4pt] &= 8\sin(\dfrac{π}{6})\sin(\dfrac{π}{3}) \\[4pt] &= 8(\dfrac{1}{2})\dfrac{\sqrt{3}}{2} \\[4pt] &= 2\sqrt{3} \\[4pt] z &=ρ\cos φ \\[4pt] &= 8\cos(\dfrac{π}{6}) \\[4pt] &= 8(\dfrac{\sqrt{3}}{2}) \\[4pt] &= 4\sqrt{3} \end{align*}\]

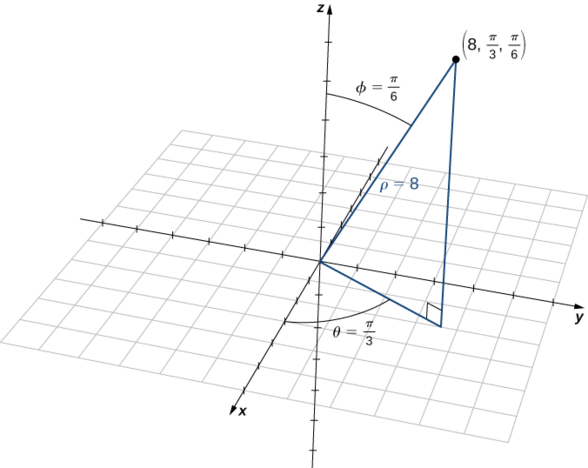
Takwimu hii ni quadrant ya kwanza ya mfumo wa kuratibu 3-dimensional. Ina uhakika kinachoitwa “(8, pi/3, pi/6).” Kuna sehemu ya mstari kutoka kwa asili hadi hatua. Inaitwa “rho = 8.” Pembe kati ya sehemu hii ya mstari na mhimili wa z-inaitwa “phi = pi/6.” Kuna sehemu ya mstari katika ndege ya x y kutoka asili hadi kivuli cha uhakika. Pembe kati ya x-axis na r inaitwa “theta = pi/3.” — Kielelezo$\PageIndex{12}$: Makadirio ya uhakika katika$xy$ -ndege ni$4$ vitengo kutoka asili. Mstari kutoka kwa asili hadi makadirio ya uhakika huunda angle ya$π/3$ na chanya$x$ -axis. uhakika uongo$4\sqrt{3}$ vitengo juu$xy$ -ndege.

Hatua na kuratibu za spherical$(8,\dfrac{π}{3},\dfrac{π}{6})$ ina kuratibu mstatili$(2,2\sqrt{3},4\sqrt{3}).$

Kupata maadili katika kuratibu za cylindrical ni sawa sawa:

\[ \begin{align*} r&=ρ \sin φ \\[4pt] &= 8\sin \dfrac{π}{6} &=4 \\[4pt] θ&=θ \\[4pt] z&=ρ\cos φ\\[4pt] &= 8\cos\dfrac{π}{6} \\[4pt] &= 4\sqrt{3} .\end{align*}\]

Hivyo, kuratibu cylindrical kwa uhakika ni$(4,\dfrac{π}{3},4\sqrt{3})$.

Zoezi$\PageIndex{4}$

Panda hatua na kuratibu za spherical$(2,−\frac{5π}{6},\frac{π}{6})$ na kuelezea eneo lake katika kuratibu zote za mstatili na za cylindrical.

Kidokezo

Kubadili kuratibu kwanza kunaweza kusaidia kupata eneo la uhakika katika nafasi kwa urahisi zaidi.

Jibu

Cartesian:$(−\frac{\sqrt{3}}{2},−\frac{1}{2},\sqrt{3}),$ cylindrical:$(1,−\frac{5π}{6},\sqrt{3})$

$Takwimu hii ni ya mfumo wa kuratibu 3-dimensional. Ina uhakika. Kuna sehemu ya mstari kutoka kwa asili hadi hatua. Pembe kati ya sehemu hii ya mstari na mhimili wa z ni phi. Kuna sehemu ya mstari katika ndege ya x y kutoka asili hadi kivuli cha point.Pembe kati ya x-axis na rho ni theta.$

Mfano$\PageIndex{5}$: Converting from Rectangular Coordinates

Badilisha kuratibu za mstatili$(−1,1,\sqrt{6})$ kwa kuratibu zote mbili na za cylindrical.

Suluhisho

Anza kwa kubadili kutoka mstatili hadi kuratibu za spherical:

\[ \begin{align*} ρ^2 &=x^2+y^2+z^2=(−1)^2+1^2+(\sqrt{6})^2=8 \\[4pt] \tan θ &=\dfrac{1}{−1} \\[4pt] ρ&=2\sqrt{2} \text{ and }θ=\arctan(−1)=\dfrac{3π}{4}. \end{align*}\]

Kwa sababu$(x,y)=(−1,1)$, basi chaguo sahihi$θ$ ni$\frac{3π}{4}$.

Kuna kweli njia mbili za kutambua$φ$. Tunaweza kutumia equation$φ=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}})$. Mbinu rahisi zaidi, hata hivyo, ni kutumia equation$z=ρ\cos φ.$ Tunajua kwamba$z=\sqrt{6}$ na$ρ=2\sqrt{2}$, hivyo

$\sqrt{6}=2\sqrt{2}\cos φ,$hivyo$\cos φ=\dfrac{\sqrt{6}}{2\sqrt{2}}=\dfrac{\sqrt{3}}{2}$

na kwa hiyo$φ=\dfrac{π}{6}$. Kuratibu spherical ya uhakika ni$(2\sqrt{2},\dfrac{3π}{4},\dfrac{π}{6}).$

Ili kupata kuratibu za cylindrical kwa uhakika, tunahitaji tu kupata r:

$r=ρ\sin φ=2\sqrt{2}\sin(\dfrac{π}{6})=\sqrt{2}.$

Kuratibu za cylindrical kwa uhakika ni$(\sqrt{2},\dfrac{3π}{4},\sqrt{6})$.

Mfano$\PageIndex{6}$: Identifying Surfaces in the Spherical Coordinate System

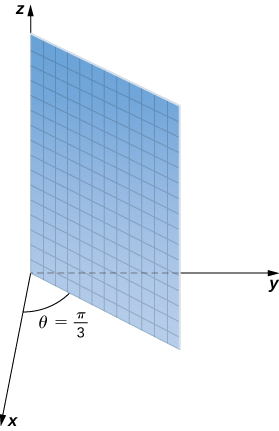
Eleza nyuso na equations zilizopewa spherical.

$θ=\dfrac{π}{3}$
$φ=\dfrac{5π}{6}$
$ρ=6$
$ρ=\sin θ \sinφ$

Suluhisho

a. variable$θ$ inawakilisha kipimo cha angle sawa katika mifumo ya kuratibu cylindrical na spherical. Pointi na kuratibu$(ρ,\dfrac{π}{3},φ)$ ziko kwenye ndege inayounda angle$θ=\dfrac{π}{3}$ na$x$ mhimili mzuri. Kwa sababu$ρ>0$, uso ilivyoelezwa na equation$θ=\dfrac{π}{3}$ ni nusu ya ndege inavyoonekana katika Kielelezo$\PageIndex{13}$.

b Equation$φ=\dfrac{5π}{6}$ inaelezea pointi zote katika mfumo spherical kuratibu kwamba uongo juu ya mstari kutoka asili kutengeneza angle kupima$\dfrac{5π}{6}$ rad na chanya$z$ -axis. Vipengele hivi huunda koni ya nusu (Kielelezo). Kwa sababu kuna thamani moja tu ya$φ$ kwamba ni kipimo kutoka chanya$z$ -axis, hatuwezi kupata koni kamili (na vipande viwili).

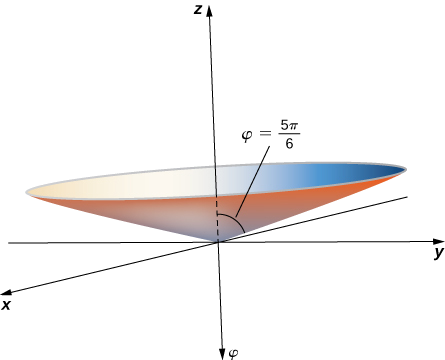
Takwimu hii ni sehemu ya juu ya koni ya elliptical. Sehemu ya chini ya koni ni asili ya mfumo wa kuratibu 3-dimensional. — Kielelezo$\PageIndex{14}$: equation$φ=\dfrac{5π}{6}$ inaelezea koni.

Ili kupata equation katika kuratibu mstatili, tumia equation$φ=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}}).$

\[ \begin{align*} \dfrac{5π}{6} &=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}}) \\[4pt] \cos\dfrac{5π}{6}&=\dfrac{z}{\sqrt{x^2+y^2+z^2}} \\[4pt] −\dfrac{\sqrt{3}}{2}&=\dfrac{z}{\sqrt{x^2+y^2+z^2}} \\[4pt] \dfrac{3}{4} &=\dfrac{z^2}{x^2+y^2+z^2} \\[4pt] \dfrac{3x^2}{4}+\dfrac{3y^2}{4}+\dfrac{3z^2}{4} &=z^2 \\[4pt] \dfrac{3x^2}{4}+\dfrac{3y^2}{4}−\dfrac{z^2}{4} &=0. \end{align*}\]

Hii ni equation ya koni unaozingatia$z$ -axis.

c. equation$ρ=6$ inaelezea seti ya pointi zote$6$ vitengo mbali na asili-nyanja na radius$6$ (Kielelezo$\PageIndex{15}$).

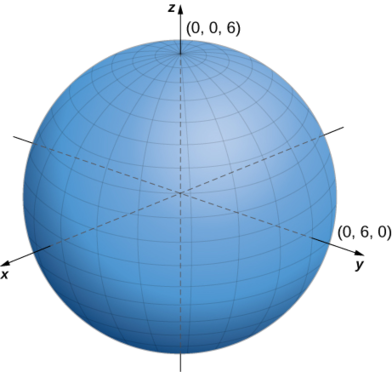
Takwimu hii ni nyanja. Mhimili wa z-ni wima kupitia katikati na huingilia nyanja saa (0, 0, 6). Mhimili wa y ni usawa kupitia katikati na huingilia nyanja saa (0, 6, 0). — Kielelezo$\PageIndex{15}$: Equation$ρ=6$ inaelezea nyanja na radius$6$.

d Ili kutambua uso huu, kubadilisha equation kutoka kuratibu spherical hadi mstatili, kwa kutumia equations$y=ρsinφ\sin θ$ na$ρ^2=x^2+y^2+z^2:$

$ρ=\sin θ \sin φ$

$ρ^2=ρ\sin θ\sin φ$Kuzidisha pande zote mbili za equation na$ρ$.

$x^2+y^2+z^2=y$Vipengele vya mstatili wa mstatili kwa kutumia milinganyo hapo juu.

$x^2+y^2−y+z^2=0$Ondoa$y$ kutoka pande zote mbili za equation.

$x^2+y^2−y+\dfrac{1}{4}+z^2=\dfrac{1}{4}$Jaza mraba.

$x^2+(y−\dfrac{1}{2})^2+z^2=\dfrac{1}{4}$. Andika upya maneno ya kati kama mraba kamilifu.

equation inaelezea nyanja unaozingatia katika hatua$(0,\dfrac{1}{2},0)$ na radius$\dfrac{1}{2}$.

Zoezi$\PageIndex{5}$

Eleza nyuso zilizoelezwa na equations zifuatazo.

$ρ=13$
$θ=\dfrac{2π}{3}$
$φ=\dfrac{π}{4}$

Kidokezo: Fikiria juu ya kile kila sehemu inawakilisha na nini inamaanisha kushikilia sehemu hiyo mara kwa mara.
Jibu: Hii ni seti ya$13$ vitengo vyote vya pointi kutoka asili. Seti hii inaunda nyanja yenye radius$13$.
Jibu b: Seti hii ya pointi huunda ndege ya nusu. Pembe kati ya ndege ya nusu na$x$ mhimili mzuri ni$θ=\dfrac{2π}{3}.$
Jibu c: Hebu$P$ kuwa hatua juu ya uso huu. Vector msimamo wa hatua hii hufanya angle ya$φ=\dfrac{π}{4}$ na chanya$z$ -axis, ambayo ina maana kwamba pointi karibu na asili ni karibu na mhimili. Vipengele hivi huunda koni ya nusu.

Kuratibu za spherical ni muhimu katika kuchambua mifumo iliyo na kiwango fulani cha ulinganifu kuhusu nukta, kama vile kiasi cha nafasi ndani ya uwanja wa kuba au kasi ya upepo katika anga ya sayari. Tufe ambayo ina equation ya Cartesian$x^2+y^2+z^2=c^2$ ina equation rahisi$ρ=c$ katika kuratibu spherical.

Katika jiografia, latitude na longitude hutumiwa kuelezea maeneo kwenye uso wa dunia, kama inavyoonekana kwenye Kielelezo. Ingawa umbo la Dunia si nyanja kamilifu, tunatumia kuratibu za spherical kuwasiliana na maeneo ya pointi duniani. Hebu tuchukue Dunia ina sura ya nyanja yenye radius$4000$ mi. Tunaelezea hatua za angle kwa digrii badala ya radians kwa sababu latitude na longitude hupimwa kwa digrii.

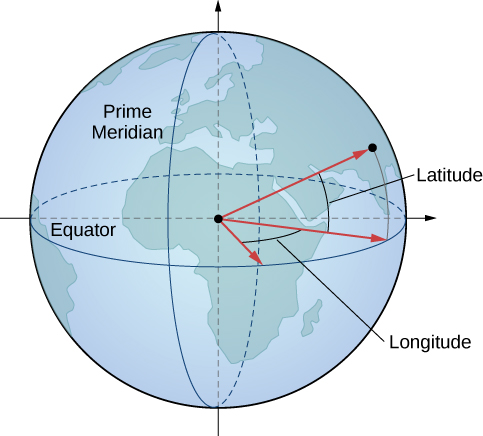
Takwimu hii ni picha ya Dunia. Ina meridian mkuu iliyoandikwa, ambayo ni mduara juu ya uso unaozunguka Dunia kwa wima kupitia miti. Ikweta inaitwa pia ambayo ni mduara usio na usawa unaozunguka Dunia. Vectors tatu hutoka katikati ya Dunia. Mbili kati yao hupanua kwa equator na zinaonyesha kipimo cha longitude. Wawili wao hupanua kwenye mduara wa polar wima na zinaonyesha kipimo cha latitude. — Kielelezo$\PageIndex{16}$: Katika mfumo wa latitude-longitude, pembe zinaelezea eneo la uhakika Duniani kuhusiana na ikweta na meridiani mkuu.

Hebu katikati ya Dunia iwe katikati ya nyanja, na ray kutoka katikati kupitia Ncha ya Kaskazini inayowakilisha$z$ mhimili mzuri. Meridian mkuu inawakilisha maelezo ya uso kama inavyozunguka$xz$ -ndege. Equator ni maelezo ya nyanja inayoingilia$xy$ -ndege.

Mfano$\PageIndex{7}$: Converting Latitude and Longitude to Spherical Coordinates

Latitude ya Columbus, Ohio, ni$40°$ N na longitude ni$83°$ W, ambayo ina maana kwamba Columbus ni$40°$ kaskazini ya ikweta. Fikiria ray kutoka katikati ya Dunia kupitia Columbus na ray kutoka katikati ya Dunia kupitia ikweta moja kwa moja kusini mwa Columbus. Kipimo cha angle kilichoundwa na mionzi ni$40°$. Kwa njia hiyo hiyo, kupima kutoka meridian mkuu, Columbus iko upande$83°$ wa magharibi. Eleza eneo la Columbus katika kuratibu za spherical.

Suluhisho

Radi ya Dunia ni$4000$ mi, hivyo$ρ=4000$. Mfululizo wa meridian mkuu na equator iko juu ya$x$ mhimili mzuri. Movement upande wa magharibi ni kisha ilivyoelezwa na hatua hasi angle, ambayo inaonyesha kwamba$θ=−83°$, Kwa sababu Columbus uongo$40°$ kaskazini ya ikweta, ni uongo$50°$ kusini mwa Ncha ya Kaskazini, hivyo$φ=50°$. Katika kuratibu spherical, Columbus iko katika hatua$(4000,−83°,50°).$

Zoezi$\PageIndex{6}$

Sydney, Australia ni katika$34°S$ na eneo$151°E.$ Express Sydney katika kuratibu spherical.

Kidokezo: Kwa sababu Sydney iko kusini mwa ikweta, tunahitaji kuongeza$90°$ ili kupata angle kipimo kutoka chanya$z$ -axis.
Jibu: $(4000,151°,124°)$

Kuratibu za cylindrical na spherical zinatupa kubadilika kuchagua mfumo wa kuratibu unaofaa kwa tatizo lililopo. Uchaguzi unaofikiria wa mfumo wa kuratibu unaweza kufanya tatizo iwe rahisi kutatua, wakati uchaguzi mbaya unaweza kusababisha mahesabu yasiyo ya lazima. Katika mfano unaofuata, tunachunguza matatizo kadhaa tofauti na kujadili jinsi ya kuchagua mfumo bora wa kuratibu kwa kila mmoja.

Mfano$\PageIndex{8}$: Choosing the Best Coordinate System

Katika kila hali zifuatazo, tunaamua ni mfumo gani wa kuratibu unaofaa zaidi na kuelezea jinsi tunavyoweza kuelekeza safu za kuratibu. Kunaweza kuwa na jibu zaidi ya moja sahihi kwa jinsi axes zinapaswa kuelekezwa, lakini tunachagua mwelekeo unaofaa katika mazingira ya tatizo. Kumbuka: Hakuna taarifa za kutosha kuanzisha au kutatua matatizo haya; sisi tu kuchagua mfumo wa kuratibu (Kielelezo$\PageIndex{17}$).

Find katikati ya mvuto wa mpira Bowling.
Kuamua kasi ya manowari chini ya sasa ya bahari.
Tumia shinikizo katika tank ya maji ya conical.
Pata kiasi cha mafuta kinachozunguka kupitia bomba.
Kuamua kiasi cha ngozi kinachohitajika kufanya mpira wa miguu.

Takwimu hii ina picha 5. Picha ya kwanza inaonyesha mipira ya bowling. Picha ya pili ni manowari inayosafiri juu ya uso wa bahari. Picha ya tatu ni koni ya trafiki. Picha ya nne ni bomba katika nchi tasa. Picha ya tano ni mpira wa miguu. — Kielelezo$\PageIndex{17}$: (mikopo: (a) mabadiliko ya kazi na scl hua, Wikimedia, (b) mabadiliko ya kazi na DVIDSHUB, Flickr, (c) mabadiliko ya kazi na Michael Malak, Wikimedia, (d) mabadiliko ya kazi na Sean Mack, Wikimedia, (e) mabadiliko ya kazi na Elvert Barnes, Flickr)

Suluhisho

Kwa wazi, mpira wa bowling ni nyanja, hivyo kuratibu za spherical ingekuwa kazi bora hapa. Asili inapaswa kuwa iko katikati ya kimwili ya mpira. Hakuna chaguo dhahiri kwa jinsi$x$ -,$y$ - na$z$ -axes zinapaswa kuelekezwa. Mipira ya Bowling kawaida ina kuzuia uzito katikati. Chaguo moja iwezekanavyo ni kuunganisha$z$ -axis na mhimili wa ulinganifu wa kuzuia uzito.
Manowari kwa ujumla huenda katika mstari wa moja kwa moja. Hakuna ulinganifu wa mzunguko au spherical ambayo inatumika katika hali hii, hivyo kuratibu mstatili ni chaguo nzuri. $z$-axis lazima pengine uhakika juu. Ya $x$- na$y$ -axes inaweza kuendana na uhakika wa mashariki na kaskazini, kwa mtiririko huo. Asili inapaswa kuwa sehemu rahisi ya kimwili, kama nafasi ya kuanzia ya manowari au eneo la bandari fulani.
Koni ina aina kadhaa za ulinganifu. Katika kuratibu cylindrical, koni inaweza kuwakilishwa na equation$z=kr,$ ambapo$k$ ni mara kwa mara. Katika kuratibu za spherical, tumeona kwamba nyuso za fomu$φ=c$ ni mbegu za nusu. Mwisho, katika kuratibu mstatili, mbegu za elliptic ni nyuso za quadric na zinaweza kusimamishwa na usawa wa fomu$z^2=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}.$ Katika kesi hii, tunaweza kuchagua yoyote ya tatu. Hata hivyo, equation kwa uso ni ngumu zaidi katika kuratibu mstatili kuliko katika mifumo mingine miwili, hivyo tunaweza kutaka kuepuka uchaguzi huo. Aidha, sisi ni kuzungumza juu ya tank maji, na kina cha maji inaweza kuja katika mchezo wakati fulani katika mahesabu yetu, hivyo inaweza kuwa nzuri kuwa na sehemu ambayo inawakilisha urefu na kina moja kwa moja. Kulingana na hoja hii, kuratibu cylindrical inaweza kuwa chaguo bora. Chagua $z$-axis ili kufanana na mhimili wa koni. Mwelekeo wa axes nyingine mbili ni kiholela. Asili inapaswa kuwa hatua ya chini ya koni.
Bomba ni silinda, hivyo kuratibu cylindrical itakuwa bora chaguo bora. Katika kesi hii, hata hivyo, tunaweza kuchagua kuelekeza $z$-axis yetu na mhimili katikati ya bomba. $x$Mhimili wa -inaweza kuchaguliwa ili kuelekeza moja kwa moja chini au kwa mwelekeo mwingine wa mantiki. Asili inapaswa kuchaguliwa kulingana na taarifa ya tatizo. Kumbuka kwamba hii inaweka $z$-axis katika mwelekeo usio na usawa, ambayo ni tofauti kidogo na kile tunachofanya kawaida. Inaweza kuwa na maana ya kuchagua mwelekeo usio wa kawaida kwa axes ikiwa ni busara kwa tatizo.
Soka ina ulinganifu wa mzunguko kuhusu mhimili wa kati, hivyo kuratibu za cylindrical zingekuwa kazi bora. $z$Mhimili lazima ufanane na mhimili wa mpira. Asili inaweza kuwa katikati ya mpira au labda moja ya ncha. Msimamo wa$x$ -axis ni kiholela.

Zoezi$\PageIndex{7}$

Ni mfumo gani wa kuratibu unaofaa zaidi kwa kuunda ramani ya nyota, kama inavyotazamwa kutoka Dunia (angalia takwimu ifuatayo)?

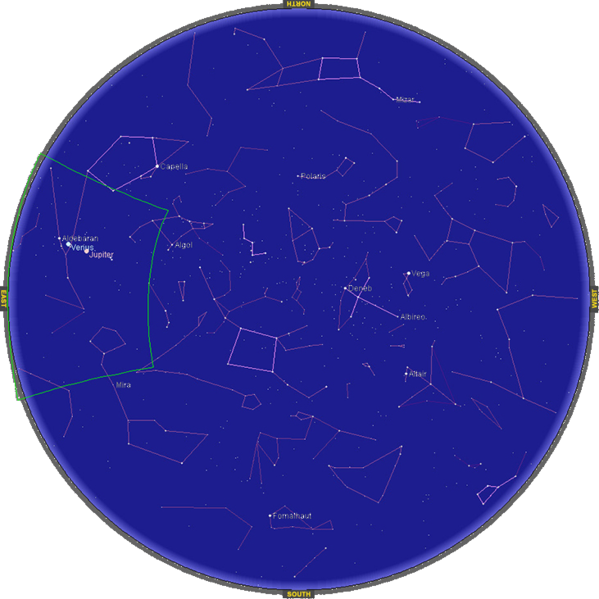
$Takwimu hii ni duara yenye chati ya nyota katikati.$

Tunapaswa kuelekezaje axes za kuratibu?

Kidokezo: Ni aina gani ya ulinganifu uliopo katika hali hii?
Jibu: Spherical kuratibu na asili iko katikati ya dunia,$z$ -axis iliyokaa na Ncha ya Kaskazini, na$x$ -axis iliyokaa na meridian mkuu

Dhana muhimu

Katika mfumo wa kuratibu wa cylindrical, hatua katika nafasi inawakilishwa na mara tatu iliyoamriwa$(r,θ,z),$ ambapo$(r,θ)$ inawakilisha kuratibu polar ya makadirio ya uhakika katika$xy$ -ndege na z inawakilisha makadirio ya uhakika kwenye$z$ -axis.
Ili kubadilisha hatua kutoka kwa kuratibu za cylindrical hadi kuratibu za Cartesian, tumia equations$x=r\cos θ, y=r\sin θ,$ na$z=z.$
Ili kubadilisha hatua kutoka kwa kuratibu za Cartesian hadi kuratibu za cylindrical, tumia equations$r^2=x^2+y^2, \tan θ=\dfrac{y}{x},$ na$z=z.$
Katika mfumo wa kuratibu wa spherical, hatua$P$ katika nafasi inawakilishwa na mara tatu iliyoamriwa$(ρ,θ,φ)$, ambapo$ρ$ umbali kati$P$ na asili$(ρ≠0), θ$ ni angle sawa inayotumiwa kuelezea eneo katika kuratibu za cylindrical, na$φ$ ni angle inayotengenezwa na chanya$z$ -axis na sehemu ya mstari$\bar{OP}$, ambapo$O$ ni asili na$0≤φ≤π.$
Ili kubadilisha hatua kutoka kwa kuratibu za spherical hadi kuratibu za Cartesian, tumia equations$x=ρ\sin φ\cos θ, y=ρ\sin φ\sin θ,$ na$z=ρ\cos φ.$
Ili kubadilisha hatua kutoka kwa kuratibu za Cartesian hadi kuratibu za spherical, tumia equations$ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},$ na$φ=\arccos(\dfrac{z}{\sqrt{x^2+y^2+z^2}})$.
Ili kubadilisha hatua kutoka kwa kuratibu za spherical hadi kuratibu za cylindrical, tumia equations$r=ρ\sin φ, θ=θ,$ na$z=ρ\cos φ.$
Ili kubadilisha hatua kutoka kwa kuratibu za cylindrical hadi kuratibu za spherical, tumia equations$ρ=\sqrt{r^2+z^2}, θ=θ,$ na$φ=\arccos(\dfrac{z}{\sqrt{r^2+z^2}}).$

faharasa

cylindrical kuratibu mfumo: njia ya kuelezea eneo katika nafasi na kuamuru mara tatu$(r,θ,z),$ ambapo$(r,θ)$ inawakilisha kuratibu polar ya makadirio ya uhakika katika$xy$ -ndege, na z inawakilisha makadirio ya uhakika kwenye$z$ -axis

mfumo wa kuratibu spherical: njia ya kuelezea eneo katika nafasi na kuamuru mara tatu$(ρ,θ,φ),$ ambapo$ρ$ ni umbali kati$P$ na asili$(ρ≠0), θ$ ni angle sawa kutumika kuelezea eneo katika kuratibu cylindrical, na$φ$ ni angle sumu na chanya$z$ -axis na line sehemu$\bar{OP}$, ambapo$O$ ni asili na$0≤φ≤π$

Wachangiaji na Majina

Template:ContribOpenStaxCalc
Paul Seeburger edited the LaTeX on the page

Ufafanuzi: Mfumo wa Kuratibu wa Cylind

Uongofu kati ya Kuratibu za Cylindrical na Cart

Mfano\(\PageIndex{1}\): Converting from Cylindrical to Rectangular Coordinates

Zoezi\(\PageIndex{1}\)

Mfano\(\PageIndex{2}\): Converting from Rectangular to Cylindrical Coordinates

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\): Identifying Surfaces in the Cylindrical Coordinate System

Zoezi\(\PageIndex{3}\)

Ufafanuzi: mfumo wa kuratibu spherical

HOWTO: Kubadilisha kati ya Mipangilio ya mviringo, ya Cylindrical, na

Mfano\(\PageIndex{4}\): Converting from Spherical Coordinates

Zoezi\(\PageIndex{4}\)

Mfano\(\PageIndex{5}\): Converting from Rectangular Coordinates

Mfano\(\PageIndex{6}\): Identifying Surfaces in the Spherical Coordinate System

Zoezi\(\PageIndex{5}\)

Mfano\(\PageIndex{7}\): Converting Latitude and Longitude to Spherical Coordinates

Zoezi\(\PageIndex{6}\)

Mfano\(\PageIndex{8}\): Choosing the Best Coordinate System

Zoezi\(\PageIndex{7}\)