12.1: Vectors katika Ndege

Last updated
Save as PDF

Page ID: 178198

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Eleza vector ya ndege, kwa kutumia notation sahihi.
Kufanya shughuli za msingi za vector (kuzidisha scalar, kuongeza, kuondoa).
Eleza vector katika fomu ya sehemu.
Eleza formula kwa ukubwa wa vector.
Express vector katika suala la vectors kitengo.
Kutoa mifano miwili ya kiasi cha vector.

Wakati wa kuelezea harakati za ndege wakati wa kukimbia, ni muhimu kuwasiliana vipande viwili vya habari: mwelekeo ambao ndege inaenda na kasi ya ndege. Wakati wa kupima nguvu, kama vile kusonga kwa inji za ndege, ni muhimu kuelezea si tu nguvu ya nguvu hiyo, lakini pia mwelekeo ambao hutumiwa. Baadhi ya kiasi, kama vile au nguvu, hufafanuliwa kwa suala la ukubwa wote (pia huitwa ukubwa) na mwelekeo. Kiasi ambacho kina ukubwa na mwelekeo huitwa vector. Katika vitabu vya vitabu, vectors mara nyingi huashiria barua za ujasiri, kama vile$\mathbf{v}$. Kwa kuwa ni vigumu kuandika kwa ujasiri wazi tunapoandika wadudu kwa mkono, tutajumuisha mshale au chusa juu ya barua inayowakilisha vector. Kufanya vectors wazi katika kitabu hiki (na kuimarisha njia unapaswa kuandika kwa mkono), tutatumia mishale au chusa juu ya barua za ujasiri (au italiki) ili kuwakilisha wadudu, kutupa$\vec v$ au$\vecs{v}$. Kumbuka kuwa baadhi ya takwimu bado zitatumia barua za ujasiri ili kuonyesha vectors.

Ufafanuzi: Vector

Vector ni kiasi ambacho kina ukubwa na mwelekeo.

Vector Uwakilishi

Vector katika ndege inawakilishwa na sehemu iliyoongozwa ya mstari (mshale). Mwisho wa sehemu huitwa hatua ya awali na hatua ya mwisho ya vector. Mshale kutoka hatua ya awali hadi hatua ya mwisho inaonyesha mwelekeo wa vector. Urefu wa sehemu ya mstari unawakilisha ukubwa wake. Tunatumia notation$\|\vecs{v}\|$ ili kuonyesha ukubwa wa vector$\vecs{v}$. Vector yenye hatua ya awali na hatua ya mwisho ambayo ni sawa inaitwa vector sifuri, iliyoashiria$\vecs{0}$. Vector sifuri ni vector pekee bila mwelekeo, na kwa mkataba inaweza kuchukuliwa kuwa na mwelekeo wowote rahisi kwa tatizo lililopo.

Vectors na ukubwa sawa na mwelekeo huitwa vectors sawa. Tunachukua wadudu sawa sawa, hata kama wana pointi tofauti za awali. Hivyo, ikiwa$\vecs{v}$ na$\vecs{w}$ ni sawa, tunaandika

\[\vecs{v}=\vecs{w}. \nonumber \]

Ufafanuzi: Vectors sawa

Vectors inasemekana kuwa vectors sawa kama wana ukubwa sawa na mwelekeo.

Mishale katika Kielelezo$\PageIndex{1 (b)}$ ni sawa. Kila mshale una urefu sawa na mwelekeo. Dhana ya karibu ni wazo la vectors sambamba. Vectors mbili inasemekana kuwa sambamba ikiwa wana maelekezo sawa au kinyume. Tunachunguza wazo hili kwa undani zaidi baadaye katika sura. Vector inaelezwa na ukubwa wake na mwelekeo, bila kujali mahali ambapo hatua yake ya awali iko.

Takwimu hii ina picha mbili. kwanza ni kinachoitwa “a” na ina line sehemu anayewakilisha vector vector v. line sehemu huanza katika hatua ya awali na inakwenda hatua terminal. Kuna mshale wa mshale kwenye hatua ya mwisho. picha ya pili ni kinachoitwa “b” na ni wadudu tano, kila kinachoitwa v ndogo 1, v ndogo 2, v ndogo 3, v ndogo 4, v ndogo 5. Wote wanaelezea katika mwelekeo huo na wana urefu sawa. — Kielelezo$\PageIndex{1}$: (a) vector inawakilishwa na sehemu iliyoongozwa ya mstari kutoka hatua yake ya awali hadi hatua yake ya mwisho. (b) Vectors$\vecs{v}_1$ kupitia$\vecs{v}_5$ ni sawa.

Matumizi ya boldface, barua za chini kwa jina la vectors ni uwakilishi wa kawaida katika kuchapishwa, lakini kuna maelezo mbadala. Wakati wa kuandika jina la vector kwa mkono, kwa mfano, ni rahisi kupiga mshale juu ya kutofautiana kuliko kuonyesha ni vector:$\vec{v}$. Wakati vector ina hatua ya awali$P$ na hatua ya mwisho$Q$, notation$\vecd{PQ}$ ni muhimu kwa sababu inaonyesha mwelekeo na eneo la vector.

Mfano$\PageIndex{1}$: Sketching Vectors

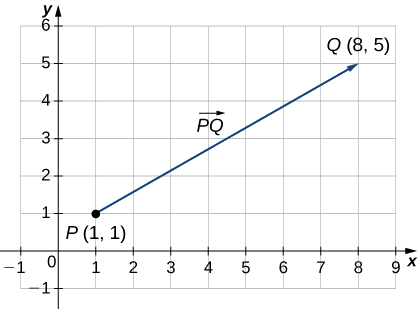
Mchoro vector katika ndege kutoka hatua ya awali$P(1,1)$ kwa uhakika terminal$Q(8,5)$.

Suluhisho

Angalia Kielelezo$\PageIndex{2}$. Kwa sababu vector huenda kutoka hatua$P$ kwa hatua$Q$, sisi jina hilo$\vecd{PQ}$.

Takwimu hii ni grafu ya quadrant ya kwanza. Kuna sehemu ya mstari kuanzia jozi iliyoamriwa (1, 1). Pia, hatua hii inaitwa “P.” Sehemu ya mstari inaisha kwenye jozi iliyoamriwa (8, 5) na inaitwa “Q.” Sehemu ya mstari inaitwa “PQ.” — Kielelezo$\PageIndex{2}$: Vector na hatua ya awali$(1,1)$ na hatua ya terminal$(8,5)$ inaitwa$\vecd{PQ}$.

Zoezi$\PageIndex{1}$

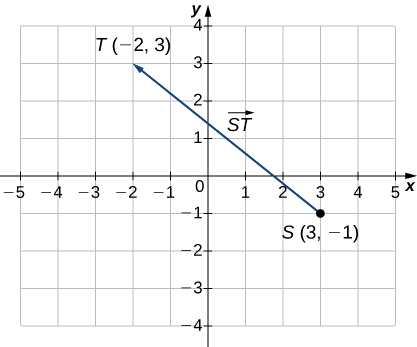
Mchoro vector$\vecd{ST}$ ambapo$S$ ni uhakika$(3,−1)$ na$T$ ni uhakika$(−2,3).$

Kidokezo: Hatua ya kwanza iliyoorodheshwa kwa jina la vector ni hatua ya awali ya vector.

Jibu: $Takwimu hii ni grafu ya mfumo wa kuratibu. Kuna sehemu ya mstari kuanzia jozi iliyoamriwa (3, -1). Pia, hatua hii inaitwa “S.” Sehemu ya mstari inaisha kwenye jozi iliyoamriwa (-2, 3) na inaitwa “T.” Kuna mshale wa mshale kwenye hatua “T,” inayowakilisha vector. Sehemu ya mstari inaitwa “ST.”$

Kuchanganya wadudu

Vectors na maombi mengi halisi ya maisha, ikiwa ni pamoja na hali kuwashirikisha nguvu au kasi. Kwa mfano, fikiria vikosi vinavyofanya mashua kuvuka mto. Motor ya mashua huzalisha nguvu katika mwelekeo mmoja, na sasa ya mto huzalisha nguvu katika mwelekeo mwingine. Vikosi vyote viwili ni vectors. Lazima tuchukue ukubwa na mwelekeo wa kila nguvu katika akaunti ikiwa tunataka kujua wapi mashua yatakwenda.

Mfano wa pili unaohusisha wadudu ni quarterback kutupa mpira wa miguu. Quarterback haina kutupa mpira sambamba na ardhi; badala yake, yeye inalenga juu katika hewa. Kasi ya kutupa kwake inaweza kuwakilishwa na vector. Kama tunajua jinsi ngumu yeye throws mpira (ukubwa-katika kesi hii, kasi), na angle (mwelekeo), tunaweza kuwaambia jinsi mbali mpira kusafiri chini ya shamba.

Nambari halisi mara nyingi huitwa scalar katika hisabati na fizikia. Tofauti na vectors, scalars kwa ujumla huchukuliwa kuwa na ukubwa tu, lakini hakuna mwelekeo. Kuzidisha vector kwa scalar hubadilisha ukubwa wa vector. Hii inaitwa kuzidisha scalar. Kumbuka kuwa kubadilisha ukubwa wa vector hauonyeshe mabadiliko katika mwelekeo wake. Kwa mfano upepo unaopiga kutoka kaskazini hadi kusini unaweza kuongezeka au kupungua kwa kasi huku ukiendeleza mwelekeo wake kutoka kaskazini hadi kusini.

Ufafanuzi: Kuzidisha kwa Scalar

Bidhaa$k\vecs{v}$ ya vector$\vecs{v}$ na scalar$k$ ni vector yenye ukubwa ambao ni$|k|$ mara ukubwa wa$\vecs{v}$, na kwa mwelekeo ambao ni sawa na mwelekeo wa$\vecs{v}$ ikiwa$k>0$, na kinyume na mwelekeo wa$\vecs{v}$ ikiwa$k<0$. Hii inaitwa kuzidisha scalar. Ikiwa$k=0$ au$\vecs{v}=\vecs{0}$, basi$k\vecs{v}=\vecs{0}.$

Kama unaweza kutarajia$k=−1$, kama, sisi kuashiria bidhaa$k\vecs{v}$ kama

\[k\vecs{v}=(−1)\vecs{v}=−\vecs{v}. \nonumber \]

Kumbuka kuwa$−\vecs{v}$ ina ukubwa sawa na$\vecs{v}$, lakini ina mwelekeo kinyume (Kielelezo$\PageIndex{3}$).

Graphic hii ina takwimu 4. Takwimu ya kwanza ni vector iliyoitwa “v.” Takwimu ya pili ni vector mara mbili kwa muda mrefu kama vector ya kwanza na inaitwa “2 v.” Takwimu ya tatu ni nusu kwa muda mrefu kama ya kwanza na inaitwa “1/2 v.” Takwimu ya nne ni vector katika mwelekeo kinyume kama wa kwanza. Ni kinachoitwa “-v.” — Kielelezo$\PageIndex{3}$: (a) Vector ya awali$ \vecs{v}$ ina$n$ vitengo vya urefu. (b) urefu wa$2n$ vitengo$2 \vecs{v}$ sawa. (c) Urefu wa$n/2$ vitengo$ \vecs{v}/2$ ni. (d) wadudu$\vecs{v}$ na$−\vecs{v}$ kuwa na urefu sawa lakini kinyume maelekezo.

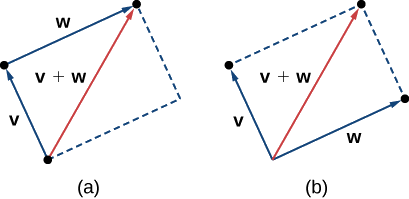
Operesheni nyingine tunaweza kufanya juu ya wadudu ni kuongeza yao pamoja katika kuongeza vector, lakini kwa sababu kila vector inaweza kuwa na mwelekeo wake mwenyewe, mchakato ni tofauti na kuongeza namba mbili. Njia ya kawaida ya graphical ya kuongeza vectors mbili ni kuweka hatua ya awali ya vector ya pili kwenye hatua ya mwisho ya kwanza, kama ilivyo kwenye Mchoro$\PageIndex{4 (a)}$. Ili kuona kwa nini hii ina maana, tuseme, kwa mfano, kwamba wadudu wote wanawakilisha makazi yao. Kama kitu hatua ya kwanza kutoka hatua ya awali kwa uhakika terminal ya vector$\vecs{v}$, basi kutoka hatua ya awali kwa uhakika terminal ya vector$\vecs{w}$, makazi yao ya jumla ni sawa na kama kitu alifanya harakati moja tu kutoka hatua ya awali kwa uhakika terminal ya vector $\vecs{v}+\vecs{w}$. Kwa sababu za wazi, mbinu hii inaitwa njia ya pembetatu. Kumbuka kwamba kama tulikuwa switched ili, hivyo kwamba$\vecs{w}$ alikuwa vector yetu ya kwanza na$\vecs{v}$ alikuwa vector yetu ya pili, tutakuwa kuishia katika sehemu moja. (Tena, angalia Kielelezo$\PageIndex{4 (a)}$.) Hivyo,

\[ \vecs{v}+ \vecs{w}= \vecs{w}+ \vecs{v}. \nonumber \]

Njia ya pili ya kuongeza vectors inaitwa njia ya parallelogram. Kwa njia hii, tunaweka vectors mbili ili wawe na hatua sawa ya awali, na kisha tunatumia parallelogram na vectors kama pande mbili zilizo karibu, kama kwenye Mchoro$\PageIndex{4 (b)}$. Urefu wa diagonal ya parallelogram ni jumla. Kulinganisha Kielelezo$\PageIndex{4 (b)}$ na Kielelezo$\PageIndex{4 (a)}$, tunaweza kuona kwamba sisi kupata jibu moja kwa kutumia njia ama. Vector$ \vecs{v}+ \vecs{w}$ inaitwa jumla ya vector.

Ufafanuzi: Vector Aidha

Jumla ya vectors mbili$\vecs{v}$ na$\vecs{w}$ inaweza kujengwa graphically kwa kuweka hatua ya awali ya$\vecs{w}$ katika hatua terminal ya$\vecs{v}$. Kisha, jumla vector$\vecs{v}+\vecs{w}$, ni vector na hatua ya awali ambayo sanjari na hatua ya awali ya$\vecs{v}$ na ina uhakika terminal kwamba sanjari na hatua terminal ya$\vecs{w}$. Operesheni hii inajulikana kama kuongeza vector.

Picha hii ina takwimu mbili. Ya kwanza ina wadudu wawili, v na w na hatua hiyo ya awali. Parallelogram inaundwa na sketching mistari iliyovunjika sambamba na vectors mbili. Mstari wa diagonal hutolewa kutoka hatua sawa ya awali hadi kona ya kinyume. Ni kinachoitwa “v + w.” Vector v huanza katika hatua ya mwisho ya vector w. parallelogram ni sumu kwa sketching mistari kuvunjwa sambamba na wadudu wawili. Mstari wa diagonal hutolewa kutoka hatua sawa ya awali kama vector w kwenye kona ya kinyume. Ni kinachoitwa “v + w.” — Kielelezo$\PageIndex{4}$: (a) Wakati wa kuongeza wadudu kwa njia ya pembetatu, hatua ya awali ya$\vecs{w}$ ni hatua ya mwisho ya$\vecs{v}$. (b) Wakati wa kuongeza vectors kwa njia ya parallelogram, vectors$\vecs{v}$ na$\vecs{w}$ kuwa na hatua sawa ya awali.

Pia ni sahihi hapa kujadili uondoaji wa vector. Sisi kufafanua$\vecs{v}−\vecs{w}$ kama$\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}$. Vector$\vecs{v}−\vecs{w}$ inaitwa tofauti ya vector. Graphically, vector$\vecs{v}−\vecs{w}$ inaonyeshwa kwa kuchora vector kutoka hatua ya mwisho ya$\vecs{w}$ hadi hatua ya mwisho ya$\vecs{v}$ (Kielelezo$\PageIndex{5}$).

Picha hii ina takwimu mbili. Takwimu ya kwanza ina vectors mbili, moja iliyoandikwa “v” na nyingine iliyoitwa “w.” Vectors wote wana hatua sawa ya awali. Vector tatu ni inayotolewa kati ya pointi terminal ya v na w. ni kinachoitwa “v — w.” Takwimu ya pili ina vectors mbili, moja iliyoandikwa “v” na nyingine iliyoandikwa “-w.” Vector “-w” ina hatua yake ya awali katika hatua ya mwisho ya “v.” Parallelogram imeundwa kwa mistari iliyovunjika ambapo “v” ni diagonal na “w” ni upande wa juu. — Kielelezo$\PageIndex{5}$: (a) Tofauti vector$\vecs{v}−\vecs{w}$ ni taswira kwa kuchora vector kutoka hatua terminal ya$\vecs{w}$ kwa uhakika terminal ya$\vecs{v}$. (b) vector$\vecs{v}−\vecs{w}$ ni sawa na vector$\vecs{v}+(−\vecs{w})$.

Katika Kielelezo$\PageIndex{4 (a)}$, hatua ya awali ya$\vecs{v}+\vecs{w}$ ni hatua ya awali ya$\vecs{v}$. Hatua ya mwisho ya$\vecs{v}+\vecs{w}$ ni hatua ya mwisho ya$\vecs{w}$. Vectors hizi tatu huunda pande za pembetatu. Inafuata kwamba urefu wa upande mmoja ni chini ya jumla ya urefu wa pande zilizobaki. Hivyo tuna

\[\|\vecs{v}+\vecs{w}\|≤\|\vecs{v}\|+\|\vecs{w}\|. \nonumber \]

Hii inajulikana zaidi kwa ujumla kama usawa wa pembetatu. Kuna kesi moja, hata hivyo, wakati vector matokeo$\vecs{u}+\vecs{v}$ ina ukubwa sawa na jumla ya ukubwa wa$\vecs{u}$ na$\vecs{v}$. Hii hutokea tu wakati$\vecs{u}$ na$\vecs{v}$ kuwa na mwelekeo sawa.

Mfano$\PageIndex{2}$: Combining Vectors

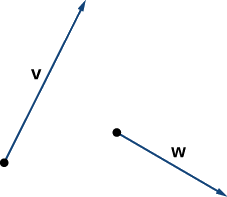
Kutokana na wadudu$\vecs{v}$ na$\vecs{w}$ inavyoonekana katika Kielelezo$\PageIndex{6}$, mchoro wadudu

$3\vecs{w}$
$\vecs{v}+\vecs{w}$
$2\vecs{v}−\vecs{w}$

Takwimu hii ina vectors mbili. Wao ni vector v na vector w. wao si kushikamana. — Kielelezo$\PageIndex{6}$: Vectors$\vecs{v}$ na$\vecs{w}$ uongo katika ndege moja.

Suluhisho

a. vector$3\vecs{w}$ ina mwelekeo sawa na$\vecs{w}$; ni mara tatu kwa muda mrefu kama$\vecs{w}$.

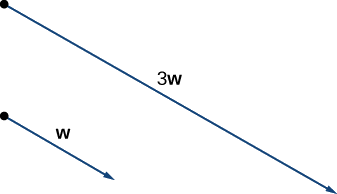
$Takwimu hii ina vectors mbili. Ya kwanza inaitwa “w.” Ya pili ni sawa na “w” na inaitwa “3w.” Ni mara tatu kwa muda mrefu kama w katika mwelekeo huo.$

Vector$3\vecs{w}$ ina mwelekeo sawa$\vecs{w}$ na ni mara tatu kwa muda mrefu.

b Tumia njia ya kuongeza ya kupata$\vecs{v}+\vecs{w}$.

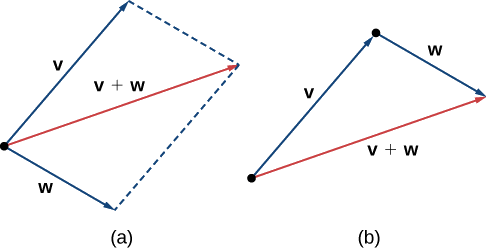
Picha hii ina takwimu mbili. Ya kwanza ina vectors mbili, kinachoitwa “v” na “w.” Wote wawili wana hatua sawa ya awali. Vector ya tatu hutolewa, iliyoandikwa “v + w.” Ni diagonal ya parallelogram sumu kwa kuwa na pande sambamba na wadudu v na w. takwimu ya pili ni pembetatu sumu kwa kuwa vector v upande mmoja na vector w karibu na v. hatua ya mwisho ya v ni hatua ya awali ya w. upande wa tatu ni kinachoitwa “v + w.” — Kielelezo$\PageIndex{7}$: Ili kupata$\vecs{v}+\vecs{w}$, kuunganisha vectors katika pointi zao za awali au kuweka hatua ya awali ya vector moja kwenye hatua ya mwisho ya nyingine. (a) Vector$\vecs{v}+\vecs{w}$ ni diagonal ya parallelogram na pande$\vecs{v}$ na$\vecs{w}$. (b) vector$\vecs{v}+\vecs{w}$ ni upande wa tatu wa pembetatu sumu na$\vecs{w}$ kuwekwa katika hatua terminal ya$\vecs{v}$.

c Ili kupata$2\vecs{v}−\vecs{w}$, tunaweza kwanza kuandika upya maneno kama$2\vecs{v}+(−\vecs{w})$. Kisha tunaweza kuteka vector$−\vecs{w}$, kisha uongeze kwenye vector$2\vecs{v}$.

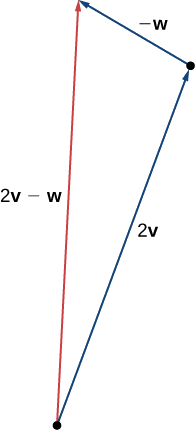
Takwimu hii ni pembetatu inayotengenezwa kwa kuwa na vector 2v upande mmoja na vector -w karibu na 2v. Hatua ya mwisho ya 2v ni hatua ya awali ya -w. Upande wa tatu unaitwa “2v - w.” — Kielelezo$\PageIndex{8}$: Ili kupata$2\vecs{v}−\vecs{w}$, ongeza tu$2\vecs{v}+(−\vecs{w})$.

Zoezi$\PageIndex{2}$

Kutumia vectors$\vecs{v}$ na$\vecs{w}$ kutoka Mfano$\PageIndex{2}$, mchoro vector$2\vecs{w}−\vecs{v}$.

Kidokezo: Mchoro wa kwanza wa vectors$2\vecs{w}$ na$−\vecs{v}$.

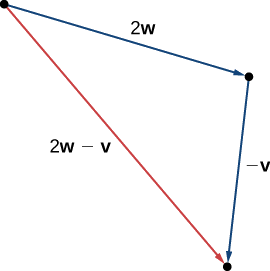
Jibu: $Takwimu hii ni pembetatu inayotengenezwa kwa kuwa na vector 2w upande mmoja na vector -v karibu na 2w. Hatua ya mwisho ya 2w ni hatua ya awali ya -v. Upande wa tatu ni kinachoitwa “2w — v.”$

Vipengele vya vector

Kufanya kazi na vectors katika ndege ni rahisi wakati tunafanya kazi katika mfumo wa kuratibu. Wakati pointi za awali na pointi za mwisho za vectors zinapewa katika kuratibu za Cartesian, hesabu zinakuwa moja kwa moja.

Mfano$\PageIndex{3}$: Comparing Vectors

Je$\vecs{v}$, na wadudu$\vecs{w}$ sawa?

$\vecs{v}$ina hatua ya awali$(3,2)$ na hatua ya mwisho$(7,2)$
$\vecs{w}$ina hatua ya awali$(1,−4)$ na hatua ya mwisho$(1,0)$

$\vecs{v}$ina hatua ya awali$(0,0)$ na hatua ya mwisho$(1,1)$
$\vecs{w}$ina hatua ya awali$(−2,2)$ na hatua ya mwisho$(−1,3)$

Suluhisho

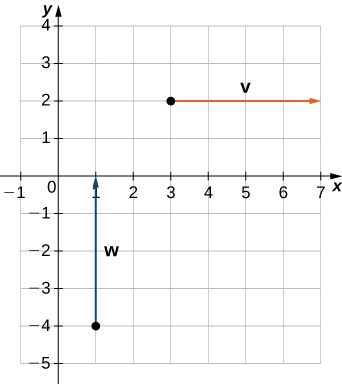
a. wadudu ni kila$4$ vitengo kwa muda mrefu, lakini wao ni oriented katika pande tofauti. Hivyo$\vecs{v}$ na$\vecs{w}$ si sawa (Kielelezo$\PageIndex{9}$).

Takwimu hii ni mfumo wa kuratibu wa Cartesian na vectors mbili. Vector kwanza kinachoitwa “v” ina hatua ya awali katika (3, 2) na hatua ya mwisho (7, 2). Ni sawa na x-axis. Vector ya pili inaitwa “w” na ina hatua ya awali (1, -4) na hatua ya mwisho (1, 0). Ni sawa na y-axis. — Kielelezo$\PageIndex{9}$: wadudu hawa si sawa.

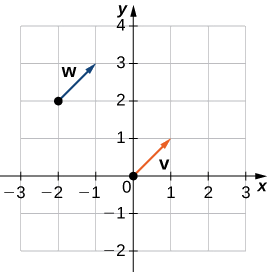
b Kulingana na Kielelezo$\PageIndex{10}$, na kutumia kidogo ya jiometri, ni wazi wadudu hawa wana urefu sawa na mwelekeo huo, hivyo$\vecs{v}$ na$\vecs{w}$ ni sawa.

Takwimu hii ni mfumo wa kuratibu wa Cartesian na vectors mbili. Vector kwanza kinachoitwa “v” ina hatua ya awali katika (0, 0) na hatua ya mwisho (1, 1). Vector ya pili inaitwa “w” na ina hatua ya awali (-2, 2) na hatua ya mwisho (-1, 3). — Kielelezo$\PageIndex{10}$: Vectors hawa ni sawa.

Zoezi$\PageIndex{3}$

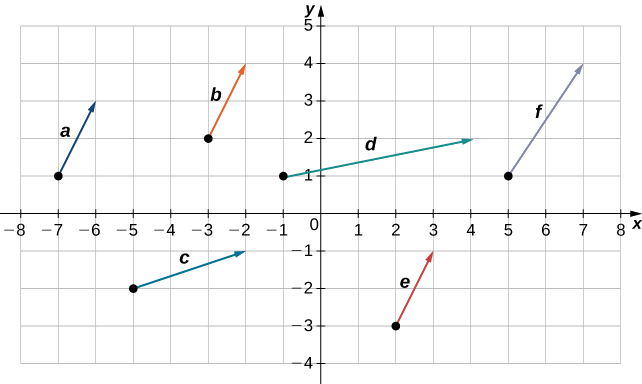
Ni ipi kati ya wadudu wafuatayo ni sawa?

$Takwimu hii ni mfumo wa kuratibu na wadudu 6, kila kinachoitwa a kupitia f. wadudu watatu, “a,” “b,” na “e” wana urefu sawa na wanaelezea katika mwelekeo huo.$

Kidokezo: Vectors sawa na ukubwa sawa na mwelekeo huo.

Jibu: Vectors$\vecs{a}, \vecs{b}$, na$\vecs{e}$ ni sawa.

Tumeona jinsi ya kupanga njama ya vector wakati tunapewa hatua ya awali na hatua ya mwisho. Hata hivyo, kwa sababu vector inaweza kuwekwa mahali popote kwenye ndege, inaweza kuwa rahisi kufanya mahesabu na vector wakati hatua yake ya awali inafanana na asili. Tunaita vector na hatua yake ya awali katika asili ya vector kiwango cha msimamo. Kwa sababu hatua ya awali ya vector yoyote katika nafasi ya kawaida inajulikana kuwa$(0,0)$, tunaweza kuelezea vector kwa kuangalia kuratibu ya hatua yake ya mwisho. Hivyo, kama vector$\vecs{v}$ ina hatua yake ya awali katika asili na hatua yake terminal katika$(x,y),$ sisi kuandika vector katika fomu sehemu kama

\[\vecs{v}=⟨x,y⟩. \nonumber \]

Wakati vector imeandikwa katika fomu ya sehemu kama hii, scalars x na y huitwa vipengele vya$\vecs{v}$.

Ufafanuzi: vipengele vya vector

Vector na hatua ya awali$(0,0)$ na hatua ya mwisho$(x,y)$ inaweza kuandikwa katika fomu ya sehemu kama

\[\vecs{v}=⟨x,y⟩. \nonumber \]

Scalars$x$ na$y$ huitwa vipengele vya$\vecs{v}$.

Kumbuka kwamba vectors ni jina na barua za chini katika aina ya ujasiri au kwa kuchora mshale juu ya jina lao. Tumejifunza pia kwamba tunaweza kutaja vector kwa fomu yake ya sehemu, na kuratibu ya hatua yake ya mwisho katika mabano ya angle. Hata hivyo, wakati wa kuandika fomu ya sehemu ya vector, ni muhimu kutofautisha kati$⟨x,y⟩$ na$(x,y)$. Jozi la kwanza lililoamriwa hutumia mabano ya angle kuelezea vector, wakati wa pili hutumia mabano kuelezea hatua katika ndege. Hatua ya awali ya$⟨x,y⟩$ ni$(0,0)$; hatua ya mwisho ya$⟨x,y⟩$ ni$(x,y)$.

Tunapokuwa na vector si tayari katika nafasi ya kawaida, tunaweza kuamua fomu yake ya sehemu kwa moja ya njia mbili. Tunaweza kutumia mbinu ya kijiometri, ambayo sisi mchoro vector katika ndege kuratibu, na kisha mchoro sawa kiwango msimamo vector. Vinginevyo, tunaweza kuipata algebraically, kwa kutumia kuratibu ya hatua ya awali na hatua ya mwisho. Ili kuipata algebraically, tunaondoa$x$ -kuratibu ya hatua ya awali kutoka$x$ -kuratibu ya hatua ya mwisho ili kupata$x$ -sehemu, na tunaondoa$y$ -kuratibu ya hatua ya awali kutoka$y$ -kuratibu ya hatua ya mwisho ili kupata$y$ -sehemu.

Kanuni: Fomu ya Kipengele cha Vector

Hebu$\vecs{v}$ kuwa vector na hatua ya awali$(x_i,y_i)$ na hatua ya mwisho$(x_t,y_t)$. Kisha tunaweza kueleza$\vecs{v}$ katika fomu ya sehemu kama$\vecs{v}=⟨x_t−x_i,y_t−y_i⟩$.

Mfano$\PageIndex{4}$: Expressing Vectors in Component Form

Express vector$\vecs{v}$ na hatua ya awali$(−3,4)$ na hatua ya mwisho$(1,2)$ katika fomu ya sehemu.

Suluhisho:

a. jiometri

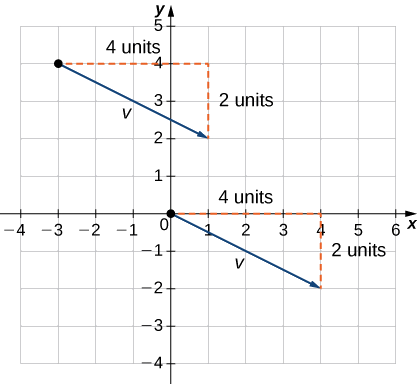
1. Mchoro vector katika ndege ya kuratibu (Kielelezo$\PageIndex{11}$).

2. Hatua ya mwisho ni vitengo 4 kwa haki na vitengo 2 chini kutoka hatua ya awali.

3. Kupata uhakika kwamba ni 4 vitengo na haki na 2 vitengo chini kutoka asili.

4. Katika nafasi ya kawaida, vector hii ina hatua ya awali$(0,0)$ na hatua ya mwisho$(4,−2)$:

$\vecs{v}=⟨4,−2⟩.$

Takwimu hii ni mfumo wa kuratibu. Kuna vectors mbili kwenye grafu. Vector ya kwanza ina hatua ya awali katika asili na hatua ya mwisho katika (4, -2). Umbali wa usawa kutoka kwa awali hadi hatua ya mwisho kwa vector inaitwa kama “vitengo 4.” Umbali wa wima kutoka kwa awali hadi hatua ya terminal inaitwa kama “vitengo 2.” Vector pili ina hatua ya awali katika (-3, 4) na terminal uhakika katika (1, 2). Umbali wa usawa kutoka kwa awali hadi hatua ya mwisho kwa vector inaitwa kama “vitengo 4.” Umbali wa wima kutoka kwa awali hadi hatua ya terminal inaitwa kama “vitengo 2.” — Kielelezo$\PageIndex{11}$: Vectors hawa ni sawa.

b. Aljebra

Katika suluhisho la kwanza, tulitumia mchoro wa vector ili kuona kwamba hatua ya mwisho iko vitengo 4 kwa haki. Tunaweza kukamilisha hili algebraically kwa kutafuta tofauti ya$x$ -kuratibu:

$x_t−x_i=1−(−3)=4.$

Vile vile, tofauti ya$y$ -kuratibu inaonyesha urefu wa wima wa vector.

$y_t−y_i=2−4=−2.$

Hivyo, katika fomu ya sehemu,

$\vecs{v}=⟨x_t−x_i,y_t−y_i⟩=⟨1−(−3),2−4⟩=⟨4,−2⟩.$

Zoezi$\PageIndex{4}$

Vector$\vecs{w}$ ina hatua ya awali$(−4,−5)$ na hatua ya mwisho$(−1,2)$. Eleza$\vecs{w}$ katika fomu ya sehemu.

Kidokezo: Unaweza kutumia njia ya kijiometri au algebraic.

Jibu: $⟨3,7⟩$

Ili kupata ukubwa wa vector, tunahesabu umbali kati ya hatua yake ya awali na hatua yake ya mwisho. Ukubwa wa vector$\vecs{v}=⟨x,y⟩$ inaashiria$\|\vecs{v}\|,$ au$|\vecs{v}|$, na inaweza kuhesabiwa kwa kutumia formula

\[\|\vecs{v}\|=\sqrt{x^2+y^2}. \nonumber \]

Kumbuka kwamba kwa sababu vector hii imeandikwa katika fomu ya sehemu, ni sawa na vector katika nafasi ya kawaida, na hatua yake ya awali katika asili na hatua ya mwisho$(x,y)$. Hivyo, inatosha kuhesabu ukubwa wa vector katika nafasi ya kawaida. Kutumia formula ya umbali ili kuhesabu umbali kati ya hatua ya awali$(0,0)$ na hatua ya mwisho$(x,y)$, tuna

\[\|\vecs{v}\|=\sqrt{(x−0)^2+(y−0)^2}=\sqrt{x^2+y^2}. \nonumber \]

Kulingana na formula hii, ni wazi kwamba kwa vector yoyote$\vecs{v}, \|\vecs{v}\|≥0,$ na$\|\vecs{v}\|=0$ kama na tu kama$\vecs{v}=\vecs{0}$.

Ukubwa wa vector pia unaweza kupatikana kwa kutumia theorem ya Pythagorean, kama ilivyo katika takwimu zifuatazo.

Takwimu hii ni pembetatu sahihi. Pande mbili zimeandikwa “x” na “y.” Hypotenuse inawakilishwa kama vector na inaitwa “mizizi ya mraba (x ^ 2 + y ^ 2).” — Kielelezo$\PageIndex{12}$: Ikiwa unatumia vipengele vya vector kufafanua pembetatu sahihi, ukubwa wa vector ni urefu wa hypotenuse ya pembetatu.

Sisi defined scalar kuzidisha na vector kuongeza kijiometri. Kuonyesha wadudu katika fomu ya sehemu inaruhusu sisi kufanya shughuli hizi sawa algebraically.

Ufafanuzi: Scalar kuzidisha na kuongeza Vector

Hebu$\vecs{v}=⟨x_1,y_1⟩$ na$\vecs{w}=⟨x_2,y_2⟩$ uwe wadudu, na$k$ uwe na scalar.

Kuzidisha Scalar:\[k\vecs{v}=⟨kx_1,ky_1⟩ \nonumber \]
Vector kuongeza:\[\vecs{v}+\vecs{w}=⟨x_1,y_1⟩+⟨x_2,y_2⟩=⟨x_1+x_2,y_1+y_2⟩ \nonumber \]

Mfano$\PageIndex{5}$: Performing Operations in Component Form

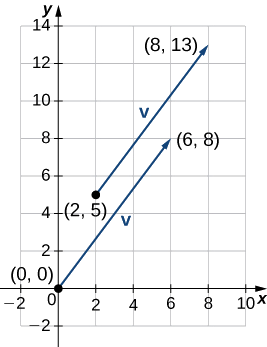
Hebu$\vecs{v}$ kuwa vector na hatua ya awali$(2,5)$ na uhakika terminal$(8,13)$, na basi$\vecs{w}=⟨−2,4⟩$.

Eleza$\vecs{v}$ katika fomu ya sehemu na upate$\|\vecs{v}\|$. Kisha, kwa kutumia algebra, tafuta
$\vecs{v}+\vecs{w}$,
$3\vecs{v}$, na
$\vecs{v}−2\vecs{w}$.

Suluhisho

Ili kuweka hatua ya awali ya asili, tunapaswa kutafsiri vitengo vya vector 2 upande wa kushoto na vitengo 5 chini (Kielelezo$\PageIndex{13}$).$\vecs{v}$ Kutumia njia ya algebraic, tunaweza kueleza$\vecs{v}$ kama$\vecs{v}=⟨8−2,13−5⟩=⟨6,8⟩$:

$\|\vecs{v}\|=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$.

Takwimu hii ni quadrant ya kwanza ya mfumo wa kuratibu. Ina vectors mbili. Vector ya kwanza ina hatua ya awali katika (2, 5) na hatua ya mwisho (8, 13). Vector ya pili ina hatua ya awali katika asili na hatua ya mwisho katika (6, 8). — Kielelezo$\PageIndex{13}$: Katika fomu ya sehemu,$\vecs{v}=⟨6,8⟩$.

b Ili kupata$\vecs{v}+\vecs{w}$, ongeza$x$ vipengele na$y$ -vipengele tofauti:

$\vecs{v}+\vecs{w}=⟨6,8⟩+⟨−2,4⟩=⟨4,12⟩.$

c Ili kupata$3\vecs{v}$, kuzidisha$\vecs{v}$ na scalar$k=3$:

$3\vecs{v}=3⋅⟨6,8⟩=⟨3⋅6,3⋅8⟩=⟨18,24⟩.$

d Ili kupata$\vecs{v}−2\vecs{w}$, pata$−2\vecs{w}$ na uongeze$\vecs{v}:$

$\vecs{v}−2\vecs{w}=⟨6,8⟩−2⋅⟨−2,4⟩=⟨6,8⟩+⟨4,−8⟩=⟨10,0⟩.$

Zoezi$\PageIndex{5A}$

Hebu$\vecs{a}=⟨7,1⟩$ na basi$\vecs{b}$ iwe vector na hatua ya awali$(3,2)$ na hatua ya terminal$(−1,−1).$

Kupata$\|\vecs{a}\|$.
Eleza$\vecs{b}$ katika fomu ya sehemu.
Kupata$3\vecs{a}−4\vecs{b}.$

Kidokezo: Tumia Theorem ya Pythagorean kupata$\|\vecs{a}\|$. Ili kupata$3\vecs{a}−4\vecs{b}$, kuanza kwa kutafuta wingi wa scalar$3\vecs{a}$ na$−4\vecs{b}$.

Jibu: $\|\vecs{a}\|=5\sqrt{2},$
Jibu b: $\vecs{b}=⟨−4,−3⟩,$
Jibu c: $3\vecs{a}−4\vecs{b}=⟨37,15⟩$

Sasa kwa kuwa tumeanzisha sheria za msingi za hesabu ya vector, tunaweza kusema mali ya shughuli za vector. Sisi kuthibitisha mbili ya mali hizi. Wengine wanaweza kuthibitishwa kwa namna hiyo.

Mali ya Uendeshaji wa Vector

Hebu$\vecs{u}, \, \vecs{v}$, na$\vecs{w}$ uwe na wadudu katika ndege. Hebu$r$ na$s$ uwe scalars.

Mali ya kubadilisha\[\vecs{u}+\vecs{v}=\vecs{v}+\vecs{u} \label{commutative} \]
Mali ya ushirika\[(\vecs{u}+\vecs{v})+\vecs{w}=\vecs{u}+(\vecs{v}+\vecs{w}) \nonumber \]
Mali ya utambulisho wa ziada\[\vecs{u}+\vecs{0}=\vecs{u} \nonumber \]
Mali isiyohamishika inverse\[\vecs{u}+(−\vecs{u})=\vecs{0} \nonumber \]
Associativity ya kuzidisha scalar\[r(s\vecs{u})=(rs)\vecs{u} \nonumber \]
Mali ya kusambaza\[(r+s)\vecs{u}=r\vecs{u}+s\vecs{u} \label{Distributive} \]
Mali ya kusambaza\[r(\vecs{u}+\vecs{v})=r\vecs{u}+r\vecs{v} \nonumber \]
Utambulisho na mali zero\[1\vecs{u}=\vecs{u}, \, 0\vecs{u}=\vecs{0} \nonumber \]

Ushahidi wa Mali Comutative

Hebu$\vecs{u}=⟨x_1,y_1⟩$ na$\vecs{v}=⟨x_2,y_2⟩.$ Tumia mali ya kubadilisha kwa idadi halisi:

\[ \begin{align*} \vecs{u}+\vecs{v} =⟨x_1+x_2,y_1+y_2⟩ \\[4pt] = ⟨x_2+x_1,y_2+y_1⟩ \\[4pt] = \vecs{v}+\vecs{u}. \end{align*}\]

□

Uthibitisho wa Mali ya Kusambaza

Tumia mali ya kusambaza kwa idadi halisi:

\[ \begin{align*} r(\vecs{u}+\vecs{v}) =r⋅⟨x_1+x_2,y_1+y_2⟩ \\[4pt] =⟨r(x_1+x_2),r(y_1+y_2)⟩ \\[4pt] = ⟨rx_1+rx_2,ry_1+ry_2⟩ \\[4pt] = ⟨rx_1,ry_1⟩+⟨rx_2,ry_2⟩ \\[4pt] = r\vecs{u}+r\vecs{v}. \end{align*}\]

□

Zoezi$\PageIndex{5B}$

Thibitisha mali ya inverse ya kuongezea.

Kidokezo: Tumia fomu ya sehemu ya vectors.

Tumegundua vipengele vya vector kutokana na pointi zake za awali na za mwisho. Katika hali nyingine, tunaweza tu kuwa na ukubwa na mwelekeo wa vector, sio pointi. Kwa wadudu hawa, tunaweza kutambua vipengele vya usawa na wima kwa kutumia trigonometry (Kielelezo$\PageIndex{14}$).

Takwimu hii ni pembetatu sahihi. Kuna angle kinachoitwa theta. pande mbili ni kinachoitwa “ukubwa wa v mara cosine theta” na “ukubwa wa v mara sine theta.” Hypotenuse inaitwa “ukubwa wa v.” — Kielelezo$\PageIndex{14}$: Vipengele vya vector huunda miguu ya pembetatu sahihi, na vector kama hypotenuse.

Fikiria angle$θ$ iliyoundwa na vector$\vecs{v}$ na chanya$x$ -axis. Tunaweza kuona kutoka pembetatu kwamba vipengele vya vector$\vecs{v}$ ni$⟨\|\vecs{v}\| \cos{θ}, \, \|\vecs{v}\| \sin {θ}⟩$. Kwa hiyo, kutokana na angle na ukubwa wa vector, tunaweza kutumia cosine na sine ya angle ili kupata vipengele vya vector.

Mfano$\PageIndex{6}$: Finding the Component Form of a Vector Using Trigonometry

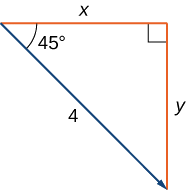
Pata fomu ya sehemu ya vector na ukubwa 4 ambayo huunda angle ya$−45°$ na$x$ -axis.

Suluhisho

Hebu$x$ na$y$ uwakilisha vipengele vya vector (Kielelezo$\PageIndex{15}$). Kisha$x=4 \cos(−45°)=2 \sqrt{2}$ na$y=4 \sin(−45°)=−2\sqrt{2}$. Fomu ya sehemu ya vector ni$⟨2\sqrt{2},−2\sqrt{2}⟩$.

Takwimu hii ni pembetatu sahihi. Pande mbili zimeandikwa “x” na “y.” Hypotenuse inaitwa “4.” Pia kuna angle iliyoitwa “digrii 45.” Hypotenuse inawakilishwa kama vector. — Kielelezo$\PageIndex{15}$: Tumia uwiano wa trigonometric,$x=\|\vecs{v}\| \cos θ$ na *$y=\|\vecs{v}\| \sin θ,$*kutambua vipengele vya vector.

Zoezi$\PageIndex{6}$

Pata fomu ya sehemu ya vector$\vecs{v}$ na ukubwa wa 10 ambayo huunda angle ya$120°$ na$x$ mhimili mzuri.

Kidokezo: $x=\|\vecs{v}\| \cos θ$na$y=\|\vecs{v}\| \sin θ$
Jibu: $\vecs v=⟨−5,5\sqrt{3}⟩$

Kitengo cha wadudu

Vector kitengo ni vector na ukubwa$1$. Kwa vector yoyote nonzero$\vecs{v}$, tunaweza kutumia scalar kuzidisha kupata kitengo vector$\vecs{u}$ ambayo ina mwelekeo sawa na$\vecs{v}$. Ili kufanya hivyo, tunazidisha vector kwa usawa wa ukubwa wake:

\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|} \vecs{v}. \nonumber \]

Kumbuka kwamba wakati sisi defined scalar kuzidisha, sisi alibainisha kuwa$\|k\vecs{v}\| =|k|⋅\|\vecs{v}\| $. Kwa$\vecs{u}=\dfrac{1}{\|\vecs{v}\| }\vecs{v}$, inafuata kwamba$\|\vecs{u}\| =\dfrac{1}{\|\vecs{v}\| }(\|\vecs{v}\| )=1$. Tunasema kwamba$\vecs{u}$ ni vector kitengo katika mwelekeo wa$\vecs{v}$ (Kielelezo$\PageIndex{16}$). Mchakato wa kutumia kuzidisha scalar kupata vector kitengo na mwelekeo fulani inaitwa kuhalalisha.

Picha hii ina takwimu mbili. Ya kwanza ni vector iliyoitwa “v.” Takwimu ya pili ni vector katika mwelekeo huo ulioitwa “u.” Vector hii ina urefu wa kitengo 1. — Kielelezo$\PageIndex{16}$: vector$\vecs{v}$ na kuhusishwa kitengo vector$\vecs{u}=\dfrac{1}{\|\vecs{v}\|}\vecs{v}$. Katika kesi hiyo,$\|\vecs{v}\|>1.$

Mfano$\PageIndex{7}$: Finding a Unit Vector

Hebu$\vecs{v}=⟨1,2⟩$.

Kupata kitengo vector na mwelekeo sawa na$\vecs{v}$.
Kupata vector$\vecs{w}$ na mwelekeo huo kama$\vecs{v}$ vile kwamba$\|\vecs{w}\|=7$.

Suluhisho:

a Kwanza, kupata ukubwa wa$\vecs{v}$, kisha ugawanye vipengele vya$\vecs{v}$ kwa ukubwa:

\[\|\vecs{v}\|=\sqrt{1^2+2^2}=\sqrt{1+4}=\sqrt{5} \nonumber \]

\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\sqrt{5}}⟨1,2⟩=⟨\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}⟩ \nonumber. \nonumber \]

b. vector$\vecs{u}$ ni katika mwelekeo sawa$\vecs{v}$ na na$\|\vecs{u}\|=1$. Tumia kuzidisha scalar kuongeza urefu wa$\vecs{u}$ bila kubadilisha mwelekeo:

\[\vecs{w}=7\vecs{u}=7⟨\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}⟩=⟨\dfrac{7}{\sqrt{5}},\dfrac{14}{\sqrt{5}}⟩ \nonumber. \nonumber \]

Zoezi$\PageIndex{7}$

Hebu$\vecs{v}=⟨9,2⟩$. Kupata vector na ukubwa$5$ katika mwelekeo kinyume kama$\vecs{v}$.

Kidokezo: Kwanza, tafuta vector kitengo katika mwelekeo sawa na$\vecs{v}$.
Jibu: $⟨−\dfrac{45}{\sqrt{85}},−\dfrac{10}{\sqrt{85}}⟩$

Tumeona jinsi rahisi inaweza kuwa kuandika vector katika fomu ya sehemu. Wakati mwingine, ingawa, ni rahisi zaidi kuandika vector kama jumla ya vector usawa na vector wima. Ili iwe rahisi zaidi, hebu tuangalie vectors ya kitengo cha kawaida. Vectors kitengo cha kawaida ni vectors$\hat{\mathbf i}=⟨1,0⟩$ na$\hat{\mathbf j}=⟨0,1⟩$ (Kielelezo$\PageIndex{17}$).

Takwimu hii ina x na y axes ya mfumo wa kuratibu katika roboduara ya kwanza. Kwenye x-axis kuna vector iliyoitwa “i,” ambayo ni sawa <1,0 — Kielelezo$\PageIndex{17}$: kiwango kitengo wadudu$\hat{\mathbf i}$ na$\hat{\mathbf j}$.

Kwa kutumia mali ya vectors, inawezekana kuelezea vector yoyote kwa suala la$\hat{\mathbf i}$ na$\hat{\mathbf j}$ katika kile tunachokiita mchanganyiko wa mstari:

\[\vecs{v}=⟨x,y⟩=⟨x,0⟩+⟨0,y⟩=x⟨1,0⟩+y⟨0,1⟩=x\hat{\mathbf i}+y\hat{\mathbf j}. \nonumber \]

Hivyo,$\vecs{v}$ ni jumla ya vector usawa na ukubwa$x$, na vector wima na ukubwa$y$, kama katika Kielelezo$\PageIndex{18}$.

Takwimu hii ni pembetatu sahihi. Upande wa usawa unaitwa “xi.” Upande wa wima umeandikwa “yj.” Hypotenuse ni vector iliyoitwa “v.” — Kielelezo$\PageIndex{18}$: vector$\vecs{v}$ ni jumla ya$x\hat{\mathbf i}$ na$y\hat{\mathbf j}$.

Mfano$\PageIndex{8}$: Using Standard Unit Vectors

Eleza vector$\vecs{w}=⟨3,−4⟩$ kwa suala la vectors ya kawaida ya kitengo.
Vector$\vecs{u}$ ni kitengo vector kwamba aina angle ya$60°$ na chanya$x$ -axis. Tumia wadudu wa kitengo cha kawaida kuelezea$\vecs{u}$.

Suluhisho:

a. kutatua vector$\vecs{w}$ katika vector na sifuri$y$ -sehemu na vector na sifuri$x$ -sehemu:

\[\vecs{w}=⟨3,−4⟩=3 \hat{\mathbf i}−4 \hat{\mathbf j}. \nonumber \]

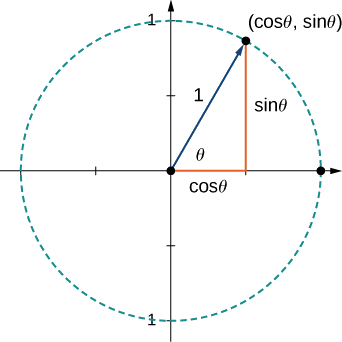
b Kwa sababu$\vecs{u}$ ni vector kitengo, hatua ya mwisho iko kwenye mduara wa kitengo wakati vector imewekwa katika nafasi ya kawaida (Kielelezo$\PageIndex{19}$).

\[ \begin{align*} \vecs{u} =⟨\cos 60°,\sin 60°⟩ \\[4pt] =⟨\dfrac{1}{2},\dfrac{\sqrt{3}}{2}⟩ \\[4pt] = \dfrac{1}{2} \hat{\mathbf i}+\dfrac{\sqrt{3}}{2} \hat{\mathbf j}. \end{align*}\]

Takwimu hii ni mduara wa kitengo. Ni mduara unaozingatia asili. Ina vector na hatua ya awali katika asili na hatua ya mwisho kwenye mduara. Hatua ya mwisho inaitwa (cos (theta), dhambi (theta)). Urefu wa vector ni kitengo 1. Pia kuna pembetatu sahihi inayoundwa na vector kama hypotenuse. Upande wa usawa unaitwa “cos (theta)” na upande wa wima huitwa “sin (theta).” — Kielelezo$\PageIndex{19}$: Hatua ya mwisho ya$\vecs{u}$ uongo kwenye mduara wa kitengo$(\cos θ, \sin θ)$.

Zoezi$\PageIndex{8}$

Hebu$\vecs{a}=⟨16,−11⟩$ na hebu$\vecs{b}$ kuwa kitengo vector kwamba aina angle ya$225°$ na chanya$x$ -axis. Express$\vecs{a}$ na$\vecs{b}$ katika suala la kiwango vectors kitengo.

Kidokezo: Tumia sine na cosine ili kupata vipengele vya$\vecs{b}$.
Jibu: $\vecs{a}=16 \hat{\mathbf i}−11 \hat{\mathbf j}, \quad \vecs{b}=−\dfrac{\sqrt{2}}{2} \hat{\mathbf i}−\dfrac{\sqrt{2}}{2} \hat{\mathbf j}$

Matumizi ya Vectors

Kwa sababu wadudu wana mwelekeo na ukubwa wote, ni zana muhimu za kutatua matatizo yanayohusisha maombi kama vile mwendo na nguvu. Kumbuka mashua mfano na quarterback mfano sisi ilivyoelezwa mapema. Hapa tunaangalia mifano mingine miwili kwa undani.

Mfano$\PageIndex{9A}$: Finding Resultant Force

Gari la Jane linakumbwa katika matope. Lisa na Jed kuja pamoja katika lori kusaidia kuvuta yake nje. Wao huunganisha mwisho mmoja wa kamba ya tow mbele ya gari na mwisho mwingine kwenye hitch ya trailer ya lori, na lori huanza kuvuta. Wakati huo huo, Jane na Jed kupata nyuma ya gari na kushinikiza. Lori huzalisha nguvu ya usawa ya 300 lb kwenye gari. Jane na Jed wanasumaji kwa pembeni kidogo zaidi na kuzalisha nguvu ya 150 lb kwenye gari. Majeshi haya yanaweza kuwakilishwa na vectors, kama inavyoonekana katika Kielelezo$\PageIndex{20}$. Pembe kati ya wadudu hawa ni 15°. Pata nguvu inayosababisha (jumla ya vector) na upe ukubwa wake kwa sehemu ya kumi ya karibu ya pound na angle yake ya mwelekeo kutoka kwa$x$ mhimili mzuri.

Picha hii ni mtazamo wa upande wa gari. Kutoka mbele ya gari kuna vector usawa kinachoitwa “paundi 300.” Pia, kutoka mbele ya gari kuna vector nyingine iliyoitwa “paundi 150.” Pembe kati ya vectors mbili ni digrii 15. — Kielelezo$\PageIndex{20}$: Vikosi viwili vinavyofanya gari kwa njia tofauti.

Suluhisho

Ili kupata athari za kuchanganya vikosi viwili, ongeza vectors yao ya mwakilishi. Kwanza, onyesha kila vector katika fomu ya sehemu au kwa mujibu wa vectors ya kitengo cha kawaida. Kwa kusudi hili, ni rahisi ikiwa tunaunganisha moja ya vectors na chanya$x$ -axis. Vector ya usawa, basi, ina hatua ya awali$(0,0)$ na hatua ya mwisho$(300,0)$. Inaweza kuelezwa kama$⟨300,0⟩$ au$300 \hat{\mathbf i}$.

Vector ya pili ina ukubwa$150$ na inafanya angle ya$15°$ na ya kwanza, hivyo tunaweza kuieleza kama$⟨150 \cos(15°),150 \sin(15°)⟩,$ au$150 \cos(15°)\hat{\mathbf i}+150 \sin(15°)\hat{\mathbf j}$. Kisha, jumla ya wadudu, au vector matokeo, ni$\vecs{r}=⟨300,0⟩+⟨150 \cos(15°),150 \sin(15°)⟩,$ na tuna

\[\|\vecs{r}\|=\sqrt{(300+150 \cos(15°))^2+(150 \sin(15°))^2}≈446.6. \nonumber \]

Pembe$θ$ iliyofanywa$\vecs{r}$ na chanya$x$ -axis ina$\tan θ=\dfrac{150 \sin 15°}{(300+150\cos 15°)}≈0.09$, hivyo$θ≈ \tan^{−1}(0.09)≈5°$, ambayo inamaanisha nguvu inayosababisha$\vecs{r}$ ina angle ya$5°$ juu ya mhimili usio na usawa.

Mfano$\PageIndex{9B}$: Finding Resultant Velocity

ndege nzi kutokana magharibi katika airspeed ya$425$ mph. Upepo unapiga kutoka kaskazini mashariki kwa$40$ mph. Je! Kasi ya chini ya ndege ni nini? Je, ni kuzaa kwa ndege?

Suluhisho

Hebu tuanze kwa kuchora hali iliyoelezwa (Kielelezo$\PageIndex{21}$).

Takwimu hii ni picha ya ndege. Kuja nje ya mbele ya ndege ni vectors mbili. Vector ya kwanza inaitwa “425” na vector ya pili inaitwa “40.” Pembe kati ya vectors ni digrii 45. — Kielelezo$\PageIndex{21}$: Awali, ndege husafiri kutokana magharibi. Upepo unatoka kaskazini mashariki, hivyo unapiga kuelekea kusini magharibi. Pembe kati ya kozi ya ndege na upepo ni$45°$. (Kielelezo si inayotolewa kwa wadogo.)

Weka mchoro ili pointi za awali za vectors ziko katika asili. Kisha, ndege ya kasi vector ni$\vecs{p}=−425\hat{\mathbf i}$. Vector kuelezea upepo hufanya angle ya$225°$ na chanya$x$ -axis:

\[\vecs{w}=⟨40 \cos(225°),40 \sin(225°)⟩=⟨−\dfrac{40}{\sqrt{2}},−\dfrac{40}{\sqrt{2}}⟩=−\dfrac{40}{\sqrt{2}}\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j}. \nonumber \]

Wakati airspeed na upepo hufanya pamoja kwenye ndege, tunaweza kuongeza vectors yao ili kupata nguvu ya matokeo:

\[\vecs{p}+\vecs{w}=−425\hat{\mathbf i}+(−\dfrac{40}{\sqrt{2}}\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j})=(−425−\dfrac{40}{\sqrt{2}})\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j}. \nonumber \]

Ukubwa wa vector matokeo inaonyesha athari za upepo kwenye kasi ya ardhi ya ndege:

$\|\vecs{p}+\vecs{w}\|=\sqrt{(−425−\dfrac{40}{\sqrt{2}})^2+(−\dfrac{40}{\sqrt{2}})^2}≈454.17$mph

Kama matokeo ya upepo, ndege inasafiri saa takriban$454$ mph jamaa na ardhi.

Kuamua kuzaa kwa ndege, tunataka kupata mwelekeo wa vector$\vecs{p}+\vecs{w}$:

$\tan θ=\dfrac{−\dfrac{40}{\sqrt{2}}}{(−425−\dfrac{40}{\sqrt{2}})}≈0.06$

$θ≈3.57°$.

Mwelekeo wa jumla wa ndege ni$3.57°$ kusini mwa magharibi.

Zoezi$\PageIndex{9}$

ndege nzi kutokana kaskazini katika airspeed ya$550$ mph. Upepo unapiga kutoka kaskazini magharibi saa$50$ mph. Je! Kasi ya chini ya ndege ni nini?

Kidokezo: Mchoro vectors na hatua sawa ya awali na kupata jumla yao.
Jibu: Takriban$516$ mph

Dhana muhimu

Vectors hutumiwa kuwakilisha kiasi ambacho kina ukubwa na mwelekeo.
Tunaweza kuongeza vectors kwa kutumia njia ya parallelogram au njia ya pembetatu ili kupata jumla. Tunaweza kuzidisha vector kwa scalar kubadili urefu wake au kutoa mwelekeo kinyume.
Kuondoa vectors hufafanuliwa kwa suala la kuongeza hasi ya vector.
vector imeandikwa katika fomu ya sehemu kama$\vecs{v}=⟨x,y⟩$.
Ukubwa wa vector ni scalar:$‖\vecs{v}‖=\sqrt{x^2+y^2}$.
Vector kitengo$\vecs{u}$ ina ukubwa$1$ na inaweza kupatikana kwa kugawanya vector kwa ukubwa wake:$\vecs{u}=\dfrac{1}{‖\vecs{v}‖}\vecs{v}$. Vectors kitengo cha kawaida ni$\hat{\mathbf i}=⟨1,0⟩$ na$\hat{\mathbf j}=⟨0,1⟩$. vector$\vecs{v}=⟨x,y⟩$ inaweza kuwa walionyesha katika suala la kiwango kitengo wadudu kama$\vecs{v}=x\hat{\mathbf i}+y\hat{\mathbf j}$.
Vectors mara nyingi hutumiwa katika fizikia na uhandisi ili kuwakilisha nguvu na kasi, kati ya kiasi kingine.

faharasa

sehemu: scalar inayoelezea ama mwelekeo wima au usawa wa vector

wadudu sawa: wadudu ambao wana ukubwa sawa na mwelekeo huo

hatua ya awali: hatua ya mwanzo ya vector

ukubwa: urefu wa vector

kuhalalisha: kutumia kuzidisha scalar kupata vector kitengo na mwelekeo fulani

njia ya parallelogram: njia ya kutafuta jumla ya vectors mbili; nafasi ya wadudu ili waweze kushiriki hatua sawa ya awali; vectors kisha kuunda pande mbili karibu ya parallelogram; jumla ya wadudu ni diagonal ya parallelogram hiyo

ya mizani: idadi halisi

kuzidisha scalar: operesheni ya vector inayofafanua bidhaa ya scalar na vector

kiwango msimamo vector: vector na hatua ya awali$(0,0)$

kiwango kitengo wadudu: vectors kitengo pamoja na axes kuratibu:$\hat{\mathbf i}=⟨1,0⟩,\, \hat{\mathbf j}=⟨0,1⟩$

hatua ya mwisho: mwisho wa vector

pembetatu usawa: urefu wa upande wowote wa pembetatu ni chini ya jumla ya urefu wa pande nyingine mbili

njia ya pembetatu: njia ya kupata jumla ya vectors mbili; nafasi ya wadudu hivyo hatua ya mwisho ya vector moja ni hatua ya awali ya nyingine; wadudu hawa kisha kuunda pande mbili za pembetatu; jumla ya wadudu ni vector inayounda upande wa tatu; hatua ya awali ya jumla ni hatua ya awali ya kwanza vector; hatua ya mwisho ya jumla ni hatua ya mwisho ya vector ya pili

kitengo vector: vector na ukubwa$1$

vector: kitu cha hisabati ambacho kina ukubwa na mwelekeo

kuongeza vector: operesheni ya vector inayofafanua jumla ya wadudu wawili

tofauti ya vector: tofauti ya vector$\vecs{v}−\vecs{w}$ inaelezwa kama$\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}$

vector jumla: jumla ya vectors mbili,$\vecs{v}$ na$\vecs{w}$, inaweza kujengwa graphically kwa kuweka hatua ya awali ya$\vecs{w}$ katika hatua ya mwisho ya$\vecs{v}$; basi vector jumla$\vecs{v}+\vecs{w}$ ni vector na hatua ya awali ambayo sanjari na hatua ya awali ya$\vecs{v}$, na kwa uhakika terminal kwamba sanjari na hatua terminal ya$\vecs{w}$

zero vector: vector na hatua zote za awali na hatua ya mwisho$(0,0)$

Ufafanuzi: Vectors sawa

Mfano\(\PageIndex{1}\): Sketching Vectors

Zoezi\(\PageIndex{1}\)

Ufafanuzi: Kuzidisha kwa Scalar

Ufafanuzi: Vector Aidha

Mfano\(\PageIndex{2}\): Combining Vectors

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\): Comparing Vectors

Zoezi\(\PageIndex{3}\)

Ufafanuzi: vipengele vya vector

Kanuni: Fomu ya Kipengele cha Vector

Mfano\(\PageIndex{4}\): Expressing Vectors in Component Form

Zoezi\(\PageIndex{4}\)

Ufafanuzi: Scalar kuzidisha na kuongeza Vector

Mfano\(\PageIndex{5}\): Performing Operations in Component Form

Zoezi\(\PageIndex{5A}\)

Mali ya Uendeshaji wa Vector

Ushahidi wa Mali Comutative

Uthibitisho wa Mali ya Kusambaza

Zoezi\(\PageIndex{5B}\)

Mfano\(\PageIndex{6}\): Finding the Component Form of a Vector Using Trigonometry

Zoezi\(\PageIndex{6}\)

Mfano\(\PageIndex{7}\): Finding a Unit Vector

Zoezi\(\PageIndex{7}\)

Mfano\(\PageIndex{8}\): Using Standard Unit Vectors

Zoezi\(\PageIndex{8}\)

Mfano\(\PageIndex{9A}\): Finding Resultant Force

Mfano\(\PageIndex{9B}\): Finding Resultant Velocity

Zoezi\(\PageIndex{9}\)