11.4: Eneo na Urefu wa Arc katika Kuratibu za Polar

Malengo ya kujifunza

• Tumia fomu ya eneo la kanda katika kuratibu za polar.
• Kuamua urefu wa arc wa curve polar.

Katika mfumo wa kuratibu mstatili, sehemu ya uhakika hutoa njia ya kuhesabu eneo chini ya pembe. Hasa, ikiwa tuna kazi\(y=f(x)\) inayofafanuliwa kutoka\(x=a\) kwa\(x=b\) wapi\(f(x)>0\) wakati huu, eneo kati ya pembe na mhimili wa x-hutolewa na

\[A=\int ^b_af(x)dx. \nonumber \]

Ukweli huu, pamoja na formula ya kutathmini hii muhimu, ni muhtasari katika Theorem ya Msingi ya Calculus. Vile vile, urefu wa arc wa curve hii hutolewa na

\[L=\int ^b_a\sqrt{1+(f′(x))^2}dx. \nonumber \]

Katika sehemu hii, tunasoma fomu zinazofanana kwa urefu wa eneo na arc katika mfumo wa kuratibu polar.

Maeneo ya Mikoa Imepakana na Curves

Sisi alisoma formula kwa eneo chini ya Curve defined katika kuratibu mstatili na curves parametrically defined. Sasa tunageuka mawazo yetu kwa kupata formula kwa eneo la eneo lililofungwa na pembe ya polar. Kumbuka kwamba ushahidi wa Theorem ya Msingi ya Calculus ilitumia dhana ya jumla ya Riemann ili kufikia eneo chini ya pembe kwa kutumia rectangles. Kwa curves polar sisi kutumia jumla Riemann tena, lakini rectangles ni kubadilishwa na sekta ya mduara.

Fikiria Curve inavyoelezwa na kazi\(r=f(θ),\) ambapo hatua\(α≤θ≤β.\) yetu ya kwanza ni kugawanya muda\([α,β]\) katika n sawa-upana subspinternations. Upana wa kila subinterval hutolewa na formula\(Δθ=(β−α)/n\), na kisha katika sehemu ya ugawaji\(θ_i\) hutolewa na formula\(θ_i=α+iΔθ\). Kila sehemu ya kugawanya\(θ=θ_i\) inafafanua mstari na mteremko\(\tan θ_i\) unaopita kupitia pole kama inavyoonekana kwenye grafu ifuatayo.

Kielelezo\(\PageIndex{1}\): Sehemu ya safu ya kawaida katika kuratibu za polar.

Makundi ya mstari yanaunganishwa na arcs ya radius ya mara kwa mara. Hii inafafanua sekta ambazo maeneo yanaweza kuhesabiwa kwa kutumia formula ya kijiometri. Eneo la kila sekta hutumiwa kwa takriban eneo kati ya makundi ya mstari mfululizo. Kisha tunahesabu maeneo ya sekta ili takriban eneo la jumla. Njia hii inatoa Riemann jumla makadirio ya eneo la jumla. Fomu ya eneo la sekta ya mduara inaonyeshwa katika takwimu ifuatayo.

Kielelezo\(\PageIndex{2}\): Eneo la sekta ya mduara hutolewa na\(A=\dfrac{1}{2}θr^2\).

Kumbuka kwamba eneo la mduara ni\(A=πr^2\). Wakati wa kupima pembe katika radians, digrii 360 ni sawa na\(2π\) radians. Kwa hiyo sehemu ya mduara inaweza kupimwa na angle ya kati\(θ\). Sehemu ya mduara hutolewa na\(\dfrac{θ}{2π}\), hivyo eneo la sekta ni sehemu hii imeongezeka kwa eneo la jumla:

\[A=(\dfrac{θ}{2π})πr^2=\dfrac{1}{2}θr^2. \nonumber \]

Kwa kuwa eneo la sekta ya kawaida katika Kielelezo\(\PageIndex{1}\) hutolewa na\(r_i=f(θ_i)\), eneo lao katika sekta hiyo linatolewa na

\[A_i=\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]

Kwa hiyo jumla Riemann kwamba approximates eneo ni iliyotolewa na

\[A_n=\sum_{i=1}^nA_i≈\sum_{i=1}^n\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]

Tunachukua kikomo kama\(n→∞\) kupata eneo halisi:

\[A=\lim_{n→∞}A_n=\dfrac{1}{2}\int ^β_α(f(θ))^2dθ. \nonumber \]

Hii inatoa theorem ifuatayo.

Eneo la Mkoa Imepakana na Curve ya Polar

Tuseme\(f\) ni kuendelea na nonhegative juu ya muda\(α≤θ≤β\) na\(0<β−α≤2π\). Eneo la kanda lililofungwa na grafu ya\(r=f(θ)\) kati ya mistari ya radial\(θ=α\) na\(θ=β\) ni

\[\begin{align} A =\dfrac{1}{2}\int ^β_α[f(θ)]^2 dθ \\[4pt] =\dfrac{1}{2}\int ^β_αr^2 dθ. \label{areapolar}\end{align} \]

Mfano\(\PageIndex{1}\): Finding an Area of a Polar Region

Pata eneo la petal moja ya rose iliyofafanuliwa na equation\(r=3\sin(2θ).\)

Suluhisho

Grafu ya\(r=3\sin (2θ)\) ifuatavyo.

Kielelezo\(\PageIndex{3}\): Grafu ya\(r=3\sin (2θ).\)

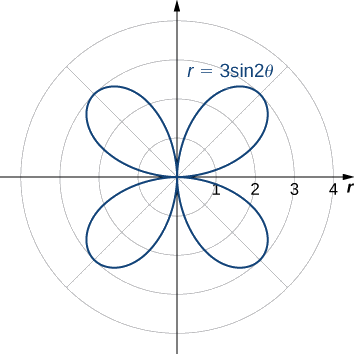
Wakati\(θ=0\) tuna\(r=3\sin(2(0))=0\). Thamani inayofuata ambayo\(r=0\) ni\(θ=π/2\). Hii inaweza kuonekana kwa kutatua equation\(3\sin (2θ)=0\) kwa\(θ\). Kwa hiyo maadili\(θ=0\) ya\(θ=π/2\) kufuatilia petal ya kwanza ya rose. Ili kupata eneo ndani ya petali hii, tumia Equation\ ref {areapolar} na\(f(θ)=3\sin (2θ), α=0,\) na\(β=π/2\):

\[\begin{align*} A &=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_0[3\sin (2θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ. \end{align*}\]

Ili kutathmini jambo hili muhimu, tumia formula\(\sin^2α=(1−\cos (2α))/2\) na\(α=2θ:\)

\[\begin{align*} A &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ \\[4pt] &=\dfrac{9}{2}\int ^{π/2}_0\dfrac{(1−\cos(4θ))}{2}dθ \\[4pt] &=\dfrac{9}{4}(\int ^{π/2}_01−\cos(4θ)dθ) \\[4pt] &=\dfrac{9}{4}(θ−\dfrac{\sin(4θ)}{4}∣^{π/2}_0 \\[4pt] &=\dfrac{9}{4}(\dfrac{π}{2}−\dfrac{\sin 2π}{4})−\dfrac{9}{4}(0−\dfrac{\sin 4(0)}{4}) \\[4pt] &=\dfrac{9π}{8}\end{align*}\]

Zoezi\(\PageIndex{1}\)

Pata eneo ndani ya cardioid iliyoelezwa na equation\(r=1−\cos θ\).

Kidokezo

Tumia Equation\ ref {eneo la eneo}. Hakikisha kuamua mipaka sahihi ya ushirikiano kabla ya kutathmini.

Jibu

\(A=3π/2\)

Mfano\(\PageIndex{1}\) kushiriki kutafuta eneo ndani ya Curve moja. Tunaweza pia kutumia Equation\ ref {areapolar} ili kupata eneo kati ya curves mbili za polar. Hata hivyo, mara nyingi tunahitaji kupata pointi za makutano ya curves na kuamua ni kazi gani inayofafanua safu ya nje au curve ya ndani kati ya pointi hizi mbili.

Mfano\(\PageIndex{2}\): Finding the Area between Two Polar Curves

Pata eneo nje ya cardioid\(r=2+2\sin θ\) na ndani ya mduara\(r=6\sin θ\).

Suluhisho

Kwanza kuteka grafu iliyo na curves zote mbili kama inavyoonekana.

Kielelezo\(\PageIndex{4}\): kanda kati ya curves\(r=2+2\sin θ\) na\(r=6\sin θ.\)

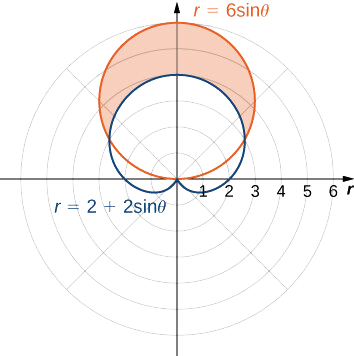
Kuamua mipaka ya ushirikiano, kwanza kupata pointi za makutano kwa kuweka kazi mbili sawa na kila mmoja na kutatua kwa\(θ\):

\[\begin{align*} 6 \sin θ &=2+2\sin θ \\[4pt] 4\sin θ &=2 \\[4pt] \sin θ &=\dfrac{1}{2} \end{align*}. \nonumber \]

Hii inatoa ufumbuzi\(θ=\dfrac{π}{6}\) na\(θ=\dfrac{5π}{6}\), ambayo ni mipaka ya ushirikiano. Mduara\(r=3\sin θ\) ni grafu nyekundu, ambayo ni kazi ya nje, na cardioid\(r=2+2\sin θ\) ni grafu ya bluu, ambayo ni kazi ya ndani. Ili kuhesabu eneo kati ya curves, kuanza na eneo ndani ya mduara kati\(θ=\dfrac{π}{6}\) na\(θ=\dfrac{5π}{6}\), kisha uondoe eneo ndani ya cardioid kati\(θ=\dfrac{π}{6}\) na\(θ=\dfrac{5π}{6}\):

\(A=\text{circle}−\text{cardioid}\)

\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}[6\sin θ]^2dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}[2+2\sin θ]^2dθ\)

\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}36\sin^2θ\,dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}4+8\sin θ+4\sin^2θ\,dθ\)

\(=18\int ^{5π/6}_{π/6}\dfrac{1−\cos(2θ)}{2}dθ−2\int ^{5π/6}_{π/6}1+2\sin θ+\dfrac{1−\cos(2θ)}{2}dθ\)

\(=9[θ−\dfrac{\sin(2θ)}{2}]^{5π/6}_{π/6}−2[\dfrac{3θ}{2}−2\cos θ−\dfrac{\sin(2θ)}{4}]^{5π/6}_{π/6}\)

\(=9(\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})−9(\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})−(3(\dfrac{5π}{6})−4\cos\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})+(3(\dfrac{π}{6})−4\cos\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})\)

\(=4π\).

Zoezi\(\PageIndex{2}\)

Pata eneo ndani ya mduara\(r=4\cos θ\) na nje ya mduara\(r=2\).

Kidokezo

Matumizi Equation\ ref {areapolar} na kuchukua faida ya ulinganifu.

Jibu

\(A=\dfrac{4π}{3}+2\sqrt{3}\)

Katika Mfano\(\PageIndex{2}\) tulipata eneo ndani ya mduara na nje ya cardioid kwa kwanza kutafuta pointi zao za makutano. Kumbuka kwamba kutatua equation moja kwa moja kwa\(θ\) kujitoa ufumbuzi mbili:\(θ=\dfrac{π}{6}\) na\(θ=\dfrac{5π}{6}\). Hata hivyo, katika grafu kuna pointi tatu za makutano. Hatua ya tatu ya makutano ni asili. Sababu kwa nini hatua hii hakuwa na show up kama suluhisho ni kwa sababu asili ni juu ya grafu zote mbili lakini kwa maadili tofauti ya\(θ\). Kwa mfano, kwa cardioid tunapata

\[\begin{align*} 2+2\sin θ =0 \\[4pt] \sin θ =−1 ,\end{align*}. \nonumber \]

hivyo maadili kwa\(θ\) kuwa kutatua equation hii ni\(θ=\dfrac{3π}{2}+2nπ\), ambapo\(n\) ni integer yoyote. Kwa mduara tunayopata

\[6\sin θ=0. \nonumber \]

ufumbuzi wa equation hii ni ya fomu\(θ=nπ\) kwa thamani yoyote integer ya\(n\). Seti hizi mbili za ufumbuzi hazina pointi sawa. Bila kujali ukweli huu, curves intersect katika asili. Kesi hii lazima izingatiwe daima.

Urefu wa safu katika Curves Polar

Hapa tunapata formula kwa urefu wa arc wa curve iliyoelezwa katika kuratibu za polar. Katika kuratibu mstatili, urefu wa arc wa curve parameterized\((x(t),y(t))\) kwa\(a≤t≤b\) hutolewa na

\[L=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}dt. \nonumber \]

Katika kuratibu polar sisi kufafanua Curve na equation\(r=f(θ)\), ambapo\(α≤θ≤β.\) Ili kukabiliana na safu urefu formula kwa Curve polar, sisi kutumia equations

\[x=r\cos θ=f(θ)\cos θ \nonumber \]

na

\[y=r\sin θ=f(θ)\sin θ, \nonumber \]

na sisi kuchukua nafasi ya parameter\(t\) na\(θ\). Kisha

\[\dfrac{dx}{dθ}=f′(θ)\cos θ−f(θ)\sin θ \nonumber \]

\[\dfrac{dy}{dθ}=f′(θ)\sin θ+f(θ)\cos θ. \nonumber \]

Sisi kuchukua nafasi\(dt\) na\(dθ\), na mipaka ya chini na ya juu ya ushirikiano ni\(α\) na\(β\), kwa mtiririko huo. Kisha formula ya urefu wa arc inakuwa

\[ \begin{align*} L &=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \\[4pt] &=\int ^β_α\sqrt{\left(\dfrac{dx}{dθ}\right)^2+\left(\dfrac{dy}{dθ}\right)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ)\cos θ−f(θ)\sin θ)^2+(f′(θ)\sin θ+f(θ)\cos θ)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2(\cos^2 θ+\sin^2 θ)+(f(θ))^2(\cos^2 θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2+(f(θ))^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ \end{align*}\]

Hii inatupa theorem ifuatayo.

Urefu wa Arc wa Curve Inafafanuliwa na Kazi ya Polar

Hebu\(f\) kuwa kazi ambayo derivative inaendelea kwa muda\(α≤θ≤β\). Urefu wa grafu ya\(r=f(θ)\) kutoka\(θ=α\) kwa\(θ=β\) ni

\[ \begin{align} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \label{arcpolar1} \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ. \label{arcpolar2} \end{align} \]

Mfano\(\PageIndex{3}\): Finding the Arc Length of a cardioid

Pata urefu wa arc wa cardioid\(r=2+2\cos θ\).

Suluhisho

Wakati\(θ=0,r=2+2\cos 0 =4.\) Zaidi ya hayo, kama\(θ\) huenda kutoka\(0\) kwa\(2π\), cardioid ni chanzo chake hasa mara moja. Kwa hiyo hii ni mipaka ya ushirikiano. Kutumia\(f(θ)=2+2\cos θ, α=0,\) na\(β=2π,\) Equation\ ref {arcpolar1} inakuwa

\[\begin{align*} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{[2+2\cos θ]^2+[−2\sin θ]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4\cos^2θ+4\sin^2θ}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4(\cos^2θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{8+8\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ. \end{align*}\]

Kisha, kwa kutumia utambulisho\(\cos(2α)=2\cos^2α−1,\) kuongeza 1 kwa pande zote mbili na kuzidisha na 2. Hii inatoa\(2+2\cos(2α)=4\cos^2α.\) Substituting\(α=θ/2\) inatoa\(2+2\cos θ=4\cos^2(θ/2)\), hivyo muhimu inakuwa

\[\begin{align*} L &= 2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{4\cos^2(\dfrac{θ}{2})}\,dθ \\[4pt] &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ.\end{align*}\]

Thamani kamili ni muhimu kwa sababu cosine ni hasi kwa maadili fulani katika uwanja wake. Ili kutatua suala hili, mabadiliko ya mipaka kutoka\(0\) kwa\(π\) na mara mbili jibu. Mkakati huu kazi kwa sababu cosine ni chanya kati\(0\) na\(\dfrac{π}{2}\). Hivyo,

\[\begin{align*} L &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ \\[4pt] &=8\int ^π_0 \cos(\dfrac{θ}{2})\,dθ \\[4pt] &=8(2\sin(\dfrac{θ}{2})∣^π_0 \\[4pt] &=16\end{align*}\]

Zoezi\(\PageIndex{3}\)

Kupata jumla safu urefu wa\(r=3\sin θ\).

Kidokezo

Tumia Equation\ ref {arcpolar1}. Kuamua mipaka sahihi, fanya meza ya maadili.

Jibu

\(s=3π\)

Dhana muhimu

• Eneo la kanda katika kuratibu za polar zilizoelezwa\(r=f(θ)\) na equation na\(α≤θ≤β\) hutolewa na muhimu\(A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\).
• Ili kupata eneo kati ya curves mbili katika mfumo wa kuratibu polar, kwanza pata pointi za makutano, kisha uondoe maeneo yanayofanana.
• Urefu wa arc wa curve ya polar iliyofafanuliwa\(r=f(θ)\) na equation na\(α≤θ≤β\) hutolewa na muhimu\(L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ\).

Mlinganyo muhimu

• Eneo la mkoa uliowekwa na pembe ya polar\[A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ=\dfrac{1}{2}\int ^β_αr^2dθ \nonumber \]
• Urefu wa arc ya curve ya polar\[L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ \nonumber \]