10.1: Mfululizo wa Nguvu na Kazi

Last updated
Save as PDF

Page ID: 178100

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tambua mfululizo wa nguvu na kutoa mifano yao.
Kuamua radius ya kuunganisha na muda wa kuunganishwa kwa mfululizo wa nguvu.
Tumia mfululizo wa nguvu ili kuwakilisha kazi.

Mfululizo wa nguvu ni aina ya mfululizo na masharti yanayohusisha variable. Zaidi hasa, kama variable ni$x$, basi masharti yote ya mfululizo kuhusisha nguvu ya$x$. Matokeo yake, mfululizo wa nguvu unaweza kufikiriwa kama polynomial isiyo na kipimo. Mfululizo wa nguvu hutumiwa kuwakilisha kazi za kawaida na pia kufafanua kazi mpya. Katika sehemu hii sisi kufafanua nguvu mfululizo na kuonyesha jinsi ya kuamua wakati mfululizo nguvu hujiunga na wakati diverges. Pia tunaonyesha jinsi ya kuwakilisha kazi fulani kwa kutumia mfululizo wa nguvu.

Fomu ya Mfululizo wa Nguvu

Mfululizo wa fomu

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots , \nonumber \]

ambapo$x$ ni variable na coefficients$c_n$ ni constants, inajulikana kama mfululizo nguvu. Mfululizo

\[1+x+x^2+\ldots =\sum_{n=0}^∞x^n \nonumber \]

ni mfano wa mfululizo wa nguvu. Kwa kuwa mfululizo huu ni mfululizo wa kijiometri na uwiano$r=|x|$, tunajua kwamba hujiunga ikiwa$|x|<1$ na hutofautiana ikiwa$|x|≥1.$

Ufafanuzi$\PageIndex{1}$: Power Series

Mfululizo wa fomu

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots \nonumber \]

ni mfululizo wa nguvu$x=0.$ unaozingatia katika mfululizo wa fomu

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

ni nguvu mfululizo unaozingatia katika$x=a$.

Ili kufanya ufafanuzi huu sahihi, tunasema kwamba$x^0=1$ na$(x−a)^0=1$ hata wakati$x=0$ na$x=a$, kwa mtiririko huo.

Mfululizo

\[\sum_{n=0}^∞\dfrac{x^n}{n!}=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\ldots \nonumber \]

\[\sum_{n=0}^∞n!x^n=1+x+2!x^2+3!x^3+\ldots \nonumber \]

wote ni nguvu mfululizo unaozingatia$x=0.$ katika mfululizo

\[\sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}=1+\dfrac{x−2}{2⋅3}+\dfrac{(x−2)^2}{3⋅3^2}+\dfrac{(x−2)^3}{4⋅3^3}+\ldots \nonumber \]

ni nguvu mfululizo unaozingatia katika$x=2$.

Kuunganishwa kwa Mfululizo wa Nguvu

Kwa kuwa maneno katika mfululizo nguvu kuhusisha variable$x$, mfululizo inaweza kugeuka kwa maadili fulani ya$x$ na kuachana kwa maadili mengine ya$x$. Kwa mfululizo wa nguvu unaozingatia$x=a$, thamani ya mfululizo katika$x=a$ hutolewa na$c_0$. Kwa hiyo, mfululizo wa nguvu daima hujiunga katikati yake. Baadhi ya mfululizo nguvu hujiunga tu kwa kuwa thamani ya$x$. Wengi nguvu mfululizo, hata hivyo, hujiunga kwa thamani zaidi ya moja ya$x$. Katika hali hiyo, mfululizo wa nguvu hujiunga na nambari zote halisi$x$ au hujiunga$x$ kwa wote kwa muda wa mwisho. Kwa mfano, mfululizo wa kijiometri$\displaystyle \sum_{n=0}^∞x^n$ hujiunga$x$ kwa wote kwa muda$(−1,1)$, lakini hutofautiana kwa wote$x$ nje ya muda huo. Sasa tunafupisha uwezekano huu wa tatu kwa mfululizo wa nguvu ya jumla.

Kumbuka$\PageIndex{1}$: Convergence of a Power Series

Fikiria mfululizo$\displaystyle \sum_{n=0}^∞c_n(x−a)^n.$ wa nguvu Mfululizo hutimiza moja ya mali zifuatazo:

Mfululizo hujiunga$x=a$ na hutofautiana kwa wote$x≠a.$
Mfululizo hujiunga kwa namba zote halisi$x$.
Kuna idadi halisi$R>0$ kama kwamba mfululizo hujiunga kama$|x−a|<R$ na diverges kama$|x−a|>R$. Katika maadili$x$ ambapo |X-a|=R, mfululizo unaweza kugeuza au kutofautiana.

Ushahidi

Tuseme kwamba mfululizo wa nguvu unazingatia$a=0$. (Kwa mfululizo unaozingatia kwa thamani ya zaidi ya sifuri, matokeo hufuata kwa kuruhusu$y=x−a$ na kuzingatia mfululizo

\[ \sum_{n=1}^∞c_ny^n. \nonumber \]

Lazima kwanza kuthibitisha ukweli wafuatayo:

Ikiwa kuna nambari halisi$d≠0$ kama$\displaystyle \sum_{n=0}^∞c_nd^n$ inayogeuka, basi mfululizo$\displaystyle \sum_{n=0}^∞c_nx^n$ hujiunga kabisa kwa$x$ vile vyote$|x|<|d|.$

Tangu$\displaystyle \sum_{n=0}^∞c_nd^n$ hujiunga, neno la nth$c_nd^n→0$ lilikuwa$n→∞$. Kwa hiyo, kuna integer$N$ kama kwamba$|c_nd^n|≤1$ kwa wote$n≥N.$ Writing

\[|c_nx^n|=|c_nd^n| \left|\dfrac{x}{d}\right|^n, \nonumber \]

tunahitimisha kwamba, kwa wote N,

\[|c_nx^n|≤\left|\dfrac{x}{d}\right|^n. \nonumber \]

Mfululizo

\[\sum_{n=N}^∞\left|\dfrac{x}{d}\right|^n \nonumber \]

ni mfululizo wa kijiometri ambao hujiunga kama$|\dfrac{x}{d}|<1.$ Kwa hiyo, kwa mtihani wa kulinganisha, tunahitimisha kwamba$\displaystyle \sum_{n=N}^∞c_nx^n$ pia hujiunga$|x|<|d|$. Kwa kuwa tunaweza kuongeza idadi ya mwisho ya maneno kwa mfululizo unaobadilika, tunahitimisha kuwa$\displaystyle \sum_{n=0}^∞c_nx^n$ hujiunga$|x|<|d|.$

Kwa matokeo haya, sasa tunaweza kuthibitisha theorem. Fikiria mfululizo

\[\sum_{n=0}^∞a_nx^n \nonumber \]

na hebu$S$ iwe seti ya namba halisi ambazo mfululizo hujiunga. Tuseme kwamba kuweka$S={0}.$ Kisha mfululizo iko chini ya kesi i.

Tuseme kwamba kuweka$S$ ni seti ya namba zote halisi. Kisha mfululizo iko chini ya kesi ii. Tuseme$S$ kwamba$S≠{0}$ na si seti ya idadi halisi. Kisha kuna idadi halisi$x*≠0$ kama vile mfululizo hauunganishi. Hivyo, mfululizo hauwezi kuungana kwa yeyote$x$ kama hiyo$|x|>|x*|$. Kwa hiyo, kuweka$S$ lazima iwe kuweka mipaka, ambayo ina maana kwamba lazima iwe na kifungo kidogo cha juu. (Ukweli huu unafuata kutoka angalau Upper Bound Mali kwa idadi halisi, ambayo ni zaidi ya wigo wa maandishi haya na ni kufunikwa katika kozi halisi uchambuzi.) Wito kwamba ndogo juu amefungwa$R$. Tangu$S≠{0}$, idadi$R>0$. Kwa hiyo, mfululizo hujiunga$|x|<R,$ na$x$ hayo yote na mfululizo huanguka katika kesi iii.

□

Ikiwa mfululizo$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ huanguka katika kesi ii. ya Kumbuka, basi mfululizo hujiunga kwa$x$ vile vile$|x−a|<R$ kwa baadhi$R>0$, na hutofautiana kwa yote$x$ hayo$|x−a|>R$. Mfululizo inaweza kugeuza au kupatanisha katika maadili$x$ ambapo$|x−a|=R$. Seti ya maadili$x$ ambayo mfululizo$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ hujiunga inajulikana kama muda wa kuungana. Kwa kuwa mfululizo unatofautiana kwa maadili yote$x$ ambapo$|x−a|>R$, urefu wa muda ni$2R$, na kwa hiyo, radius ya muda ni$R$. Thamani$R$ inaitwa radius ya kuunganisha. Kwa mfano, tangu mfululizo$\displaystyle \sum_{n=0}^∞x^n$ hujiunga kwa maadili yote$x$ katika kipindi$(−1,1)$ na hutofautiana kwa maadili yote$x$ kama vile$|x|≥1$, muda wa kuunganishwa kwa mfululizo huu ni$(−1,1)$. Kwa kuwa urefu wa muda ni$2$, radius ya muunganiko ni$1$.

Ufafanuzi: radius ya muunganiko

Fikiria mfululizo wa nguvu$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$. Seti ya namba halisi$x$ ambapo mfululizo hujiunga ni muda wa kuungana. Kama kuna idadi halisi$R>0$ kama kwamba mfululizo hujiunga$|x−a|<R$ na diverges kwa$|x−a|>R,$ basi$R$ ni Radius ya muunganiko. Kama mfululizo hujiunga tu$x=a$, tunasema Radius ya muunganiko ni$R=0$. Ikiwa mfululizo unajiunga kwa namba zote halisi$x$, tunasema radius ya kuunganisha ni$R=∞$ (Kielelezo$\PageIndex{1}$).

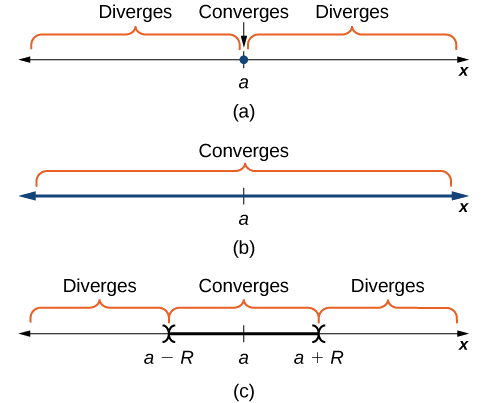
Takwimu hii ina mistari ya simu tatu, kila kinachoitwa na x. katikati ya kila mstari namba ni hatua kinachoitwa a. namba ya kwanza line ina “diverges” juu ya yote ya mstari wa kushoto wa na “diverges” juu ya mstari na haki ya. katika hatua yenyewe, ni kinachoitwa kama “converges”. Mstari wa pili wa nambari una “hujiunga” iliyoandikwa kwa mstari mzima. Nambari ya tatu ya mstari ina pointi zilizoandikwa kwenye A-R, a, na A+R. upande wa kushoto wa A-R, mstari wa nambari umeandikwa “hutofautiana”. Kati ya A-r na A+r mstari wa nambari umeandikwa “hujiunga” na kwa haki ya A+r mstari wa nambari umeandikwa “hupungua”. — Kielelezo$\PageIndex{1}$: Kwa mfululizo$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ grafu (a) inaonyesha radius ya muunganiko katika$R=0$, grafu (b) inaonyesha radius ya muunganiko katika$R=∞$, na grafu (c) inaonyesha radius ya muunganiko katika$R$. Kwa grafu (c) tunaona kwamba mfululizo unaweza au hauwezi kugeuka kwenye mwisho$x=a+R$ na$x=a−R$.

Kuamua muda wa kuunganisha kwa mfululizo wa nguvu, sisi kawaida hutumia mtihani wa uwiano. Katika Mfano$\PageIndex{1}$, sisi kuonyesha uwezekano tatu tofauti mfano katika Kielelezo$\PageIndex{1}$.

Mfano$\PageIndex{1}$: Finding the Interval and Radius of Convergence

Kwa kila mfululizo wafuatayo, pata muda na radius ya kuungana.

$\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}$
$\displaystyle \sum_{n=0}^∞n!x^n$
$\displaystyle \sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}$

Suluhisho

a Ili uangalie muunganiko, tumia mtihani wa uwiano. Tuna

\ [kuanza {align*} ρ &=\ lim_ {n → Δ}\ kushoto|\ dfrac {\ dfrac {x^ {n+1}} {(n+1)!}}} {\ dfrac {x ^ n} {n!}} \ haki|\ [4pt]
&=\ lim_ {n → Δ}\ kushoto|\ dfrac {x^ {n+1}} {(n+1)!} \ drac {n!} {x ^ n}\ kulia|\\ [4pt]
&=\ lim_ {n → Δ}\ kushoto|\ dfrac {x^ {n+1}} {(n+1) n!} \ drac {n!} {x^n}\ kulia|\\ [4pt]
&=\ lim_ {n → Δ}\ kushoto|\ dfrac {x} {n+1}\ haki|\ [4pt]
&=|x|\ lim_ {n → Δ}\ dfrac {1} {n+1}\ [4pt]
&=0<1\ mwisho {align*}\]

kwa maadili yote ya$x$. Kwa hiyo, mfululizo hujiunga na namba zote halisi$x$. Muda wa muunganiko ni$(−∞,∞)$ na radius ya muunganiko ni$R=∞.$

b Tumia mtihani wa uwiano. Kwa$x≠0$, tunaona kwamba

\ [kuanza {align*} ρ &=\ lim_ {n → Δ}\ kushoto|\ dfrac {(n+1)! x^ {n+1}} {n! x ^ n}\ kulia|\\ [4pt]
&=\ lim_ {n → Δ} | (n+1) x|\\ [4pt]
&=|x|\ lim_ {n → Δ} (n+1)\\ [4pt]
&=Δ. \ mwisho {align*}\]

Kwa hiyo, mfululizo hupungua kwa wote$x≠0$. Kwa kuwa mfululizo unazingatia$x=0$, ni lazima uunganishe huko, hivyo mfululizo unajiunga tu$x≠0$. Muda wa kuunganisha ni thamani moja$x=0$ na radius ya muunganiko ni$R=0$.

c Ili kutumia mtihani wa uwiano, fikiria

\ [kuanza {align*} ρ &=\ lim_ {n → Δ}\ kushoto|\ dfrac {\ dfrac {(x-1) ^ {n+1}} {(n+2) 3^ {n+1}}} {\ dfrac {(x-1) ^n} {(n+1) 3 ^ n}\ haki|\\ [4pt]
&=\\ lim_ {n → Δ}\ kushoto|\ dfrac {(x-1) ^ {n+1}} {n+2) 3^ {n+1}}}}}\ dfrac {(n+1) 3^n} {(x-1) ^n}\ haki|\ [4pt]
&=\ lim_ {n → Δ}\ kushoto|\ frac {(x-1) (n+1) (n+1))} {3 (n+2)}\ haki|\\ [4 pt]
&=\ dfrac {|x-2|} {3}. \ mwisho {align*}\]

uwiano$ρ<1$ kama$|x−2|<3$. Tangu$|x−2|<3$ ina maana kwamba$−3<x−2<3,$ mfululizo hujiunga kabisa kama$−1<x<5$. uwiano$ρ>1$ kama$|x−2|>3$. Kwa hiyo, mfululizo hutofautiana ikiwa$x<−1$ au$x>5$. Uwiano mtihani ni inconclusive kama$ρ=1$. Uwiano$ρ=1$ ikiwa na tu ikiwa$x=−1$ au$x=5$. Tunahitaji kupima maadili haya ya$x$ tofauti. Kwa$x=−1$, mfululizo hutolewa na

\[ \sum_{n=0}^∞\dfrac{(−1)^n}{n+1}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots . \nonumber \]

Kwa kuwa hii ni mfululizo wa harmonic mbadala, hujiunga. Hivyo, mfululizo hujiunga$x=−1$. Kwa$x=5$, mfululizo hutolewa na

\[ \sum_{n=0}^∞\dfrac{1}{n+1}=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\ldots . \nonumber \]

Hii ni mfululizo wa harmonic, ambao ni tofauti. Kwa hiyo, mfululizo wa nguvu unatofautiana$x=5$. Tunahitimisha kuwa muda wa kuungana ni$[−1,5)$ na radius ya kuunganisha ni$R=3$.

Zoezi$\PageIndex{1}$

Pata muda na radius ya kuunganisha kwa mfululizo

\[ \sum_{n=1}^∞\dfrac{x^n}{\sqrt{n}}. \nonumber \]

Kidokezo: Tumia mtihani wa uwiano ili uangalie muunganiko kabisa.

Jibu: Muda wa muunganiko ni Radius$[−1,1).$ ya muunganiko ni$R=1.$

Kuwakilisha Kazi kama Mfululizo wa Power

Kuwa na uwezo wa kuwakilisha kazi kwa “polynomial isiyo na mwisho” ni chombo chenye nguvu. Kazi nyingi ni kazi rahisi za kuchambua, kwani zinahusisha tu shughuli za msingi za hesabu za kuongeza, kuondoa, kuzidisha, na mgawanyiko. Ikiwa tunaweza kuwakilisha kazi ngumu na polynomial isiyo na kipimo, tunaweza kutumia uwakilishi wa polynomial ili kutofautisha au kuunganisha. Kwa kuongeza, tunaweza kutumia toleo la truncated la kujieleza kwa polynomial kwa maadili ya takriban ya kazi. Kwa hiyo, swali ni, lini tunaweza kuwakilisha kazi kwa mfululizo wa nguvu?

Fikiria tena mfululizo wa kijiometri

\[1+x+x^2+x^3+\ldots =\sum_{n=0}^∞x^n. \nonumber \]

Kumbuka kwamba mfululizo wa kijiometri

\[a+ar+ar^2+ar^3+\ldots \nonumber \]

converges kama na tu kama$|r|<1.$ Katika kesi hiyo, ni converges kwa$\dfrac{a}{1−r}$. Kwa hiyo, kama$|x|<1$, mfululizo katika Mfano$\PageIndex{1}$ hujiunga$\dfrac{1}{1−x}$ na tunaandika

\[1+x+x^2+x^3+\ldots =\dfrac{1}{1−x} for|x|<1. \nonumber \]

Matokeo yake, tunaweza kuwakilisha kazi$f(x)=\dfrac{1}{1−x}$ kwa mfululizo wa nguvu

\[1+x+x^2+x^3+\ldots when|x|<1. \nonumber \]

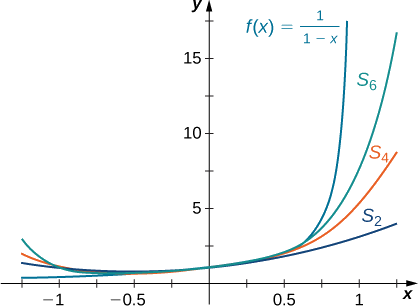
Sasa tunaonyesha graphically jinsi mfululizo huu hutoa uwakilishi$f(x)=\dfrac{1}{1−x}$ kwa kazi kwa kulinganisha grafu ya$f$ na grafu ya kadhaa ya kiasi cha sehemu ya mfululizo huu usio.

Mfano$\PageIndex{2}$: Graphing a Function and Partial Sums of its Power Series

Mchoro grafu ya$f(x)=\dfrac{1}{1−x}$ na grafu ya kiasi sambamba sehemu$ \displaystyle S_N(x)=\sum_{n=0}^Nx^n$$N=2,4,6$ kwa muda$(−1,1)$. Maoni juu ya makadirio$S_N$ kama$N$ ongezeko.

Suluhisho

Kutoka graph katika Kielelezo unaweza kuona kwamba kama$N$ ongezeko,$S_N$ inakuwa makadirio bora$f(x)=\dfrac{1}{1−x}$ kwa ajili ya$x$ katika kipindi$(−1,1)$.

Takwimu hii ni grafu ya y = 1/ (1-x), ambayo ni safu inayoongezeka na asymptote ya wima saa 1. Pia kwenye grafu hii ni sehemu tatu kiasi cha kazi, S ndogo 6, S ndogo 4, na S ndogo 2. Curves hizi, ili, hatua kwa hatua kuwa flatter. — Kielelezo$\PageIndex{2}$: Grafu inaonyesha kazi na makadirio matatu yake kwa kiasi cha sehemu ya mfululizo wa nguvu.

Zoezi$\PageIndex{2}$

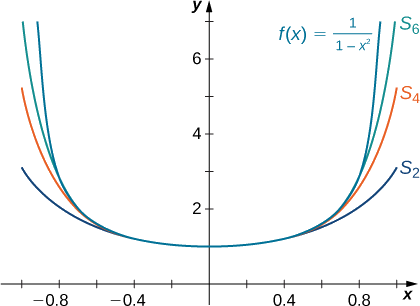
Mchoro grafu ya$f(x)=\dfrac{1}{1−x^2}$ na sambamba sehemu kiasi$\displaystyle S_N(x)=\sum_{n=0}^Nx^{2n}$$N=2,4,6$ kwa muda$(−1,1).$

Kidokezo: $S_N(x)=1+x^2+\ldots +x^{2N}=\dfrac{1−x^{2(N+1)}}{1−x^2}$

Jibu: $Takwimu hii ni grafu ya y = 1/ (1-x ^ 2), ambayo ni concave ya curve up, symmetrical kuhusu mhimili y. Pia kwenye grafu hii ni sehemu tatu kiasi cha kazi, S ndogo 6, S ndogo 4, na S ndogo 2. Curves hizi, ili, hatua kwa hatua kuwa flatter.$

Halafu tunazingatia kazi zinazohusisha usemi sawa na jumla ya mfululizo wa kijiometri na kuonyesha jinsi ya kuwakilisha kazi hizi kwa kutumia mfululizo wa nguvu.

Mfano$\PageIndex{3}$: Representing a Function with a Power Series

Tumia mfululizo wa nguvu ili kuwakilisha kila kazi zifuatazo$f$. Pata muda wa kuunganisha.

$f(x)=\dfrac{1}{1+x^3}$
$f(x)=\dfrac{x^2}{4−x^2}$

Suluhisho

Unapaswa kutambua kazi hii$f$ kama jumla ya mfululizo wa kijiometri, kwa sababu

\[ \dfrac{1}{1+x^3}=\dfrac{1}{1−(−x^3)}. \nonumber \]

Kutumia ukweli kwamba, kwa maana$|r|<1,\dfrac{a}{1−r}$ ni jumla ya mfululizo wa kijiometri

\[ \sum_{n=0}^∞ar^n=a+ar+ar^2+\ldots , \nonumber \]

tunaona kwamba, kwa$|−x^3|<1,$

\[ \begin{align*} \dfrac{1}{1+x^3} =\dfrac{1}{1−(−x^3)} \\[4pt] =\sum_{n=0}^∞(−x^3)^n \\[4pt] =1−x^3+x^6−x^9+\ldots . \end{align*}\]

Kwa kuwa mfululizo huu hujiunga ikiwa na tu ikiwa$|−x^3|<1$, muda wa kuungana ni$(−1,1)$, na tuna

\[ \dfrac{1}{1+x^3}=1−x^3+x^6−x^9+\ldots for|x|<1.\nonumber \]

b Kazi hii sio fomu halisi ya jumla ya mfululizo wa kijiometri. Hata hivyo, kwa kudanganywa kidogo kwa algebraic, tunaweza kuhusisha na mfululizo wa kijiometri. Kwa factoring 4 kati ya masharti mawili katika denominator, sisi kupata

\[ \begin{align*} \dfrac{x^2}{4−x^2} =\dfrac{x^2}{4(\dfrac{1−x^2}{4})}\\[4pt] =\dfrac{x^2}{4(1−(\dfrac{x}{2})^2)}.\end{align*}\]

Kwa hiyo, tuna

\ [kuanza {align*}\ dfrac {x ^ 2} {418-x ^ 2} &=\ dfrac {x ^ 2} {4 (1- (\ dfrac {x} {2}) ^2)}\\ [4pt]
&=\ dfrac {x ^ 2} {4} {1} {1} (\ dfrac {x} 2}) ^2}\\ [4pt]
&=\ sum_ {n = 0} ^Δ\ dfrac {x^2} {4} (\ dfrac {x} {2}) ^ {2n}. \ mwisho {align*}\]

Mfululizo hujiunga kwa muda mrefu kama$|(\dfrac{x}{2})^2|<1$ (kumbuka kwamba wakati$|(\dfrac{x}{2})^2|=1$ mfululizo hauingii). Kutatua kukosekana kwa usawa huu, tunahitimisha kwamba muda wa muunganiko ni$(−2,2)$ na

\ [kuanza {align*}\ dfrac {x^ 2} {4,1x^2} &=\ sum_ {n = 0} ^Δ\ dfrac {x^ {2n+2}} {4^ {n+1}}\\ [4pt]
&=\ dfrac {x^2} {4} +\ dfrac {x ^ 4} {4 ^ 2} +\ dfrac {x ^ 6} {4 ^ 3} +\ dots\ mwisho {align*}\]

kwa$|x|<2.$

Zoezi$\PageIndex{3}$

Kuwakilisha kazi kwa$f(x)=\dfrac{x^3}{2−x}$ kutumia mfululizo wa nguvu na kupata muda wa kuunganisha.

Kidokezo: Andika upya f katika fomu$f(x)=\dfrac{g(x)}{1−h(x)}$ kwa baadhi ya kazi$g$ na$h$.

Jibu: $\displaystyle \sum_{n=0}^∞\dfrac{x^{n+3}}{2^{n+1}}$na muda wa kuungana$(−2,2)$

Katika sehemu iliyobaki ya sura hii, tutaonyesha njia za kupata uwakilishi wa mfululizo wa nguvu kwa kazi nyingine nyingi, na jinsi gani tunaweza kutumia uwakilishi huu kutathmini, kutofautisha, na kuunganisha kazi mbalimbali.

Dhana muhimu

Kwa mfululizo nguvu unaozingatia katika$x=a$, moja ya yafuatayo mali tatu kushikilia:
- i. mfululizo nguvu hujiunga tu katika$x=a$. Katika kesi hii, tunasema kwamba radius ya kuunganisha ni$R=0$.
- ii. Mfululizo wa nguvu hujiunga na namba zote halisi$x$. Katika kesi hii, tunasema kwamba radius ya kuunganisha ni$R=∞$.
- iii. Kuna idadi halisi R kama kwamba mfululizo hujiunga$|x−a|<R$ na diverges kwa$|x−a|>R$. Katika kesi hiyo, radius ya muunganiko ni$R.$
Ikiwa mfululizo wa nguvu hujiunga na muda wa mwisho, mfululizo unaweza au hauwezi kugeuka kwenye mwisho.
Mtihani wa uwiano unaweza kutumika mara nyingi kuamua radius ya kuunganishwa.
Mfululizo wa kijiometri$\displaystyle \sum_{n=0}^∞x^n=\dfrac{1}{1−x}$ kwa$|x|<1$ inaruhusu sisi kuwakilisha kazi fulani kwa kutumia mfululizo wa kijiometri.

Mlinganyo muhimu

Mfululizo wa nguvu unaozingatia$x=0$

\[ \sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots n\nonumber \]

Mfululizo wa nguvu unaozingatia$x=a$

\[ \sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

faharasa

muda wa kuungana: seti ya idadi$x$ halisi ambayo mfululizo wa nguvu hujiunga

mfululizo wa nguvu: mfululizo wa fomu$\displaystyle \sum_{n=0}^∞c_nx^n$ ni mfululizo wa nguvu unaozingatia$x=0$; mfululizo wa fomu$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ ni mfululizo wa nguvu unaozingatia$x=a$

radius ya muunganiko: ikiwa kuna idadi halisi kama$R>0$ vile mfululizo wa nguvu unaozingatia$x=a$ unajiunga$|x−a|<R$ na kugeuka$|x−a|>R$, basi$R$ ni radius ya kuunganishwa; ikiwa mfululizo wa nguvu hujiunga tu$x=a$, radius ya kuunganisha ni$R=0$; ikiwa mfululizo wa nguvu converges kwa idadi yote halisi$x$, Radius ya muunganiko ni$R=∞$

Ufafanuzi\(\PageIndex{1}\): Power Series

Kumbuka\(\PageIndex{1}\): Convergence of a Power Series

Ushahidi

Ufafanuzi: radius ya muunganiko

Mfano\(\PageIndex{1}\): Finding the Interval and Radius of Convergence

Zoezi\(\PageIndex{1}\)

Mfano\(\PageIndex{2}\): Graphing a Function and Partial Sums of its Power Series

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\): Representing a Function with a Power Series

Zoezi\(\PageIndex{3}\)