7.8: Sura ya 7 Mazoezi ya Mapitio

Last updated
Save as PDF

Page ID: 178856

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika mazoezi ya 1 - 4, onyesha kama taarifa hiyo ni ya kweli au ya uongo. Thibitisha jibu lako kwa ushahidi au mfano wa kukabiliana.

1)$\displaystyle ∫e^x\sin(x)\,dx$ haiwezi kuunganishwa na sehemu.

2)$\displaystyle ∫\frac{1}{x^4+1}\,dx$ haiwezi kuunganishwa kwa kutumia sehemu ndogo.

Jibu: Uongo

3) Katika ushirikiano wa namba, kuongeza idadi ya pointi hupungua kosa.

4) Ushirikiano na sehemu unaweza daima mavuno muhimu.

Jibu: Uongo

Katika mazoezi ya 5 - 10, tathmini muhimu kwa kutumia njia maalum.

5)$\displaystyle ∫x^2\sin(4x)\,dx,$ kutumia ushirikiano na sehemu

6)$\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx,$ kutumia badala ya trigonometric

Jibu: $\displaystyle ∫\frac{1}{x^2\sqrt{x^2+16}}\,dx = −\frac{\sqrt{x^2+16}}{16x}+C$

7)$\displaystyle ∫\sqrt{x}\ln x\,dx,$ kutumia ushirikiano na sehemu

8)$\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx,$ kutumia sehemu ndogo

Jibu: $\displaystyle ∫\frac{3x}{x^3+2x^2−5x−6}\,dx = \frac{1}{10}\big(4\ln|2−x|+5\ln|x+1|−9\ln|x+3|\big)+C$

9)$\displaystyle ∫\frac{x^5}{(4x^2+4)^{5/2}}\,dx,$ kutumia badala ya trigonometric

10)$\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx,$ kutumia meza ya integrals au CAS

Jibu: $\displaystyle ∫\frac{\sqrt{4−\sin^2(x)}}{\sin^2(x)}\cos(x)\,dx = −\frac{\sqrt{4−\sin^2(x)}}{\sin(x)}−\frac{x}{2}+C$

Katika mazoezi 11 - 15, kuunganisha kutumia njia yoyote unayochagua.

11)$\displaystyle ∫\sin^2 x\cos^2 x\,dx$

12)$\displaystyle ∫x^3\sqrt{x^2+2}\,dx$

Jibu: $\displaystyle ∫x^3\sqrt{x^2+2}\,dx = \frac{1}{15}(x^2+2)^{3/2}(3x^2−4)+C$

13)$\displaystyle ∫\frac{3x^2+1}{x^4−2x^3−x^2+2x}\,dx$

14)$\displaystyle ∫\frac{1}{x^4+4}\,dx$

Jibu: $\displaystyle ∫\frac{1}{x^4+4}\,dx = \frac{1}{16}\ln(\frac{x^2+2x+2}{x^2−2x+2})−\frac{1}{8}\tan^{−1}(1−x)+\frac{1}{8}\tan^{−1}(x+1)+C$

15)$\displaystyle ∫\frac{\sqrt{3+16x^4}}{x^4}\,dx$

Katika mazoezi 16 - 18, takriban integrals kutumia utawala wa midpoint, utawala wa trapezoidal, na utawala wa Simpson kwa kutumia vipindi vinne, vinavyozunguka hadi decimals tatu.

16) [T]$\displaystyle ∫^2_1\sqrt{x^5+2}\,dx$

Jibu: $M_4=3.312,$
$T_4=3.354,$
$S_4=3.326$

17) [T]$\displaystyle ∫^{\sqrt{π}}_0e^{−\sin(x^2)}\,dx$

18) [T]$\displaystyle ∫^4_1\frac{\ln(1/x)}{x}\,dx$

Jibu: $M_4=−0.982,$
$T_4=−0.917,$
$S_4=−0.952$

Katika mazoezi 19 - 20, tathmini integrals, ikiwa inawezekana.

19)$\displaystyle ∫^∞_1\frac{1}{x^n}\,dx,$ kwa maadili$n$ gani ya je, hii muhimu hujiunga au kutofautiana?

20)$\displaystyle ∫^∞_1\frac{e^{−x}}{x}\,dx$

Jibu: takriban 0.2194

Katika mazoezi 21 - 22, fikiria kazi ya gamma iliyotolewa na$\displaystyle Γ(a)=∫^∞_0e^{−y}y^{a−1}\,dy.$

21) Onyesha kwamba$\displaystyle Γ(a)=(a−1)Γ(a−1).$

22) Kupanua kuonyesha kwamba$\displaystyle Γ(a)=(a−1)!,$ kuchukua$a$ ni integer chanya.

Gari la haraka zaidi duniani, Bugati Veyron, linaweza kufikia kasi ya juu ya kilomita 408. grafu inawakilisha kasi yake.

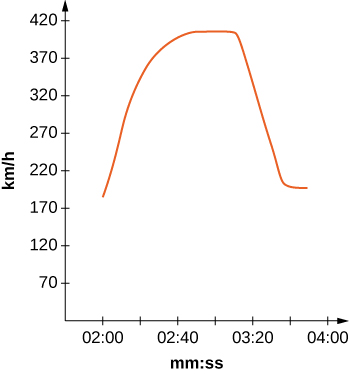
$Takwimu hii ina grafu katika quadrant ya kwanza. Inaongezeka hadi ambapo x ni takriban 03:00 mm:ss na kisha matone mbali mwinuko. Urefu wa juu wa grafu, hapa tone hutokea ni takriban 420 km/h.$

23) [T] Tumia grafu ili kukadiria kasi kila sekunde 20 na inafaa kwa grafu ya fomu$v(t)=ae^{bx}\sin(cx)+d.$ (Kidokezo: Fikiria vitengo vya wakati.)

24) [T] Kutumia kazi yako kutoka tatizo la awali, kupata hasa jinsi mbali Bugati Veyron alisafiri katika 1 min 40 sec pamoja na katika grafu.

Jibu: Majibu yanaweza kutofautiana. Ex:$9.405$ km