7.7: Integrals yasiyofaa

Malengo ya kujifunza

• Tathmini muhimu juu ya muda usio.
• Tathmini muhimu juu ya muda uliofungwa na kuacha usio na mwisho ndani ya muda.
• Tumia theorem ya kulinganisha ili kuamua kama muhimu ya uhakika ni kubadilika.

Je, ni eneo kati ya grafu ya$f(x)=\dfrac{1}{x}$ na$x$ -axis juu ya muda$[1,+∞)$ finite au usio? Kama mkoa huu ni revolved kuhusu$x$ -axis, ni kiasi finite au usio? Kushangaa, eneo la kanda lililoelezwa ni lisilo na mwisho, lakini kiasi cha imara kilichopatikana kwa kuzunguka eneo hili kuhusu$x$ -axis ni ya mwisho.

Katika sehemu hii, sisi kufafanua integrals juu ya muda usio na pamoja na integrals ya kazi zenye discontinuity juu ya muda. Integrals ya aina hizi huitwa integrals zisizofaa. Tunachunguza mbinu kadhaa za kutathmini integrals zisizofaa, zote ambazo zinahusisha kuchukua mipaka.

Kuunganisha juu ya Muda usio na mwisho

Jinsi gani sisi kwenda kuhusu kufafanua muhimu ya aina$\displaystyle \int ^{+∞}_af(x)\,dx?$ Tunaweza kuunganisha$\displaystyle \int ^t_af(x)\,dx$ kwa thamani yoyote ya$t$, hivyo ni busara kuangalia tabia ya muhimu hii kama sisi mbadala maadili kubwa ya$t$. Kielelezo$\PageIndex{1}$ inaonyesha kwamba$\displaystyle \int ^t_af(x)\,dx$ inaweza kutafsiriwa kama eneo kwa ajili ya maadili mbalimbali ya$t$. Kwa maneno mengine, tunaweza kufafanua muhimu yasiyofaa kama kikomo, kuchukuliwa kama moja ya mipaka ya ongezeko ushirikiano au itapungua bila amefungwa.

Kielelezo$\PageIndex{1}$: Ili kuunganisha kazi juu ya muda usio, tunazingatia kikomo cha muhimu kama kikomo cha juu kinaongezeka bila kufungwa.

Ufafanuzi: yasiyofaa muhimu

1. Hebu$f(x)$ uendelee juu ya muda wa fomu$[a,+∞)$. Kisha $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx, \label{improper1}$$ zinazotolewa kikomo hiki ipo.
2. Hebu$f(x)$ uendelee juu ya muda wa fomu$(−∞,b]$. Kisha $$\int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx, \label{improper2}$$ zinazotolewa kikomo hiki ipo.

Katika kila kesi, ikiwa kikomo kipo, basi jambo lisilofaa linasemekana kugeuka. Ikiwa kikomo haipo, basi jambo lisilofaa linasemekana kugeuka.

3. Hebu$f(x)$ uendelee kuendelea$(−∞,+∞)$. Kisha $$\int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx, \label{improper3}$$ zinazotolewa$\displaystyle \int ^0_{−∞}f(x)\,dx$ na$\displaystyle \int ^{+∞}_0f(x)\,dx$ wote wawili hujiunga. Ikiwa mojawapo ya integrals hizi mbili hutofautiana, basi$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx$ hutofautiana. (Ni inaweza kuonyeshwa kwamba, kwa kweli,$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^a_{−∞}f(x)\,dx+\int ^{+∞}_af(x)\,dx$ kwa thamani yoyote ya.).

Katika mfano wetu wa kwanza, tunarudi swali tulilofanya mwanzoni mwa sehemu hii: Je, eneo kati ya grafu ya$f(x)=\frac{1}{x}$ na$x$ -axis juu ya muda wa$[1,+∞)$ mwisho au usio na mwisho?

Mfano$\PageIndex{1}$: Finding an Area

Kuamua kama eneo kati ya grafu ya$f(x)=\dfrac{1}{x}$ na$x$ -axis juu ya muda$[1,+∞)$ ni ya mwisho au isiyo na mwisho.

Suluhisho

Sisi kwanza kufanya mchoro wa haraka wa kanda katika swali, kama inavyoonekana katika Kielelezo$\PageIndex{2}$.

Kielelezo$\PageIndex{2}$: Tunaweza kupata eneo kati ya Curve$f(x)=1/x$ na$x$ -axis kwa muda usio.

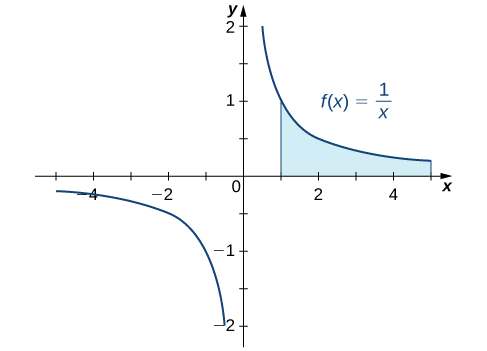
Tunaweza kuona kwamba eneo la mkoa huu linatolewa na

$$A=\int ^∞_1\frac{1}{x}\,dx. \nonumber$$

ambayo inaweza kupimwa kwa kutumia Equation\ ref {improper1}:

$$\begin{align*} A =\int ^∞_1\frac{1}{x}\,dx \nonumber \\[4pt] =\lim_{t→+∞}\int ^t_1\frac{1}{x}\,dx \tag{Rewrite the improper integral as a limit} \\[4pt] =\lim_{t→+∞}\ln |x|∣^t_1 \tag{Find the antiderivative} \\[4pt] =\lim_{t→+∞}(\ln |t|−\ln 1) \tag{Evaluate the antiderivative} \\[4pt] =+∞. \tag{Evaluate the limit.} \end{align*}$$

Kwa kuwa sehemu isiyofaa inapungua kwa eneo$+∞,$ la kanda haipatikani.

Mfano$\PageIndex{2}$: Finding a Volume

Pata kiasi cha imara iliyopatikana kwa kuzunguka eneo lililofungwa na grafu ya$f(x)=\dfrac{1}{x}$ na$x$ -axis juu ya muda$[1,+∞)$ kuhusu$x$ -axis.

Suluhisho

Imara inavyoonekana katika Kielelezo$\PageIndex{3}$. Kutumia njia ya disk, tunaona kwamba kiasi$V$ ni

$$V=π\int ^{+∞}_1\frac{1}{x^2}\,dx. \nonumber$$

Kielelezo$\PageIndex{3}$: Imara ya mapinduzi yanaweza kuzalishwa kwa kupokezana eneo lisilo na kipimo kuhusu$x$ -axis.

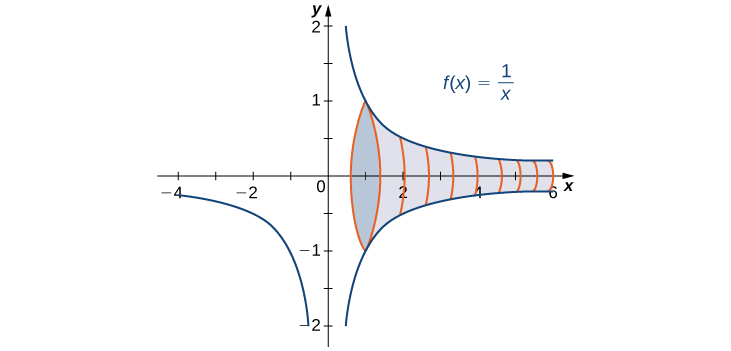
Kisha tuna

\ [Displaystyle\ kuanza {align*} V &=π\ int ^ {+Δ} _1\ frac {1} {x ^ 2}\, dx\\ [4pt]
&=π\ lim_ {t → +Δ}\ int ^t_1\ frac {1} {x^2}\, dx\ quad\\ maandishi {Andika upya kama kikomo.}\\ [4pt]
&=π\ lim_ {t → +δ}}}}} {x} {x} ^t_1\ quad\ maandishi {Pata antiderivative.}\\ [4pt]
&=π\ lim_ {t → +δ}\ kushoto (δ \ frac {1} {t} +1\ haki)\ quad\ Nakala {Tathmini antiderivative.}\\ [4pt]
&=π\ mwisho {align*}\]

muhimu yasiyofaa hujiunga na$π$. Kwa hiyo, kiasi cha imara ya mapinduzi ni$π$.

Kwa kumalizia, ingawa eneo la kanda kati ya$x$ -axis na grafu ya$f(x)=1/x$ zaidi ya muda$[1,+∞)$ ni usio, kiasi cha imara kilichozalishwa na kinachozunguka eneo hili kuhusu$x$ -axis ni mwisho. imara yanayotokana inajulikana kama Gabriel ya Pembe.

Kumbuka: Pembe ya Gabriel (pia inaitwa tarumbeta ya Torricelli) ni kielelezo cha kijiometri ambacho kina eneo la uso usio na kipimo, lakini kiasi cha mwisho. Jina linamaanisha mapokeo ya kumtambulisha Malaika Mkuu Gabrieli kama malaika anayepiga pembe kutangaza Siku ya Hukumu, akihusisha Mungu, au usio na kipimo, na mwisho. Mali za takwimu hii zilijifunza kwanza na mwanafizikia wa Italia na mwanahisabati Evangelista Torricelli katika karne ya 17.

Mfano$\PageIndex{3}$: Traffic Accidents in a City

Tuseme kwamba katika makutano ya busy, ajali za trafiki hutokea kwa kiwango cha wastani cha moja kila baada ya miezi mitatu. Baada ya wakazi kulalamika, mabadiliko yalifanywa kwa taa za trafiki katika makutano. Kwa sasa imekuwa miezi minane tangu mabadiliko yalifanywa na hakukuwa na ajali. Je, mabadiliko yamefanikiwa au ni muda wa miezi 8 bila ajali matokeo ya nafasi?

Kielelezo$\PageIndex{4}$: Mabadiliko ya kazi na David McKelvey, Flickr.

Nadharia ya uwezekano inatuambia kwamba ikiwa muda wa wastani kati ya matukio ni$k$$X$, uwezekano kwamba, wakati kati ya matukio, ni kati$a$ na$b$ hutolewa na

$$(P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber$$

wapi

$$f(x)=\begin{cases}0, \text{if}\;x<0\\ke^{−kx}, \text{if}\;x≥0\end{cases}. \nonumber$$

Hivyo, ikiwa ajali hutokea kwa kiwango cha moja kila baada ya miezi 3, basi uwezekano kwamba$X$, wakati kati ya ajali, ni kati$a$ na$b$ hutolewa na

$$P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber$$

wapi $$f(x)=\begin{cases}0, \text{if}\;x<0\\3e^{−3x}, \text{if}\;x≥0\end{cases}. \nonumber$$

Ili kujibu swali, tunapaswa kuhesabu$\displaystyle P(X≥8)=\int ^{+∞}_83e^{−3x}\,dx$ na kuamua kama inawezekana kwamba miezi 8 ingeweza kupita bila ajali ikiwa hakukuwa na uboreshaji katika hali ya trafiki.

Suluhisho

Tunahitaji kuhesabu uwezekano kama muhimu isiyofaa:

\ (\ displaystyle\ kuanza {align*} P (X≥ 8) =\ int ^ {+Δ} _83e^ {-3x}\, dx\\ [4pt]
=\ lim_ {t → +Δ}\ int ^t_83e^ {-3x}\, dx\\ [4pt]
=\ lim_ {t→ +Δ} -e ^ {-3x}\ x} ^t_8\\ [4pt]
=\ lim_ {t→ +δ} (-e ^ {-3t} +e^ {-24})\\ [4pt]
≈ 3.8×10^ {-11}. \ mwisho {align*}\)

Thamani$3.8×10^{−11}$ inawakilisha uwezekano wa ajali hakuna katika miezi 8 chini ya hali ya awali. Kwa kuwa thamani hii ni ndogo sana, ni busara kuhitimisha mabadiliko yalikuwa yenye ufanisi.

Mfano$\PageIndex{4}$: Evaluating an Improper Integral over an Infinite Interval

Tathmini$\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx.$ State kama yasiyofaa muhimu converges au diverges.

Suluhisho

Anza kwa kuandika upya$\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx$ kama kikomo kwa kutumia Equation\ ref {improper2} kutoka ufafanuzi. Hivyo,

\ [kuanza {align*}\ int ^0_ {δ}\ frac {1} {x ^ 2+4}\, dx &=\ lim_ {t → ≈}\ int ^0_t\ frac {1} {x ^ 2+4}\, dx\ quad\\ maandishi {Andika upya kama kikomo.}\\ [4pt]
&=\ lim_ {t → 1963}\ frac {1} {2}\ tan^ {-1}\ Frac {x} {2} ^0_t\ quad\ maandishi {Pata antiderivative.}\ [4pt]
&=\ lim_ {t → —Δ}\ kushoto (\ frac {1} {2}\ tan^ {1}} 0\ frac {1} {2}\ tan^ {-1}\ frac {t} {2}\ haki)\ quad\ maandishi {Tathmini antiderivative.}\\ [4pt]
&=\ Frac {π} {4}. \ quad\ maandishi {Tathmini kikomo na kurahisisha.} \ mwisho {align*}\]

Muhimu usiofaa hujiunga na$\dfrac{π}{4}.$

Mfano$\PageIndex{5}$: Evaluating an Improper Integral on $(−∞,+∞)$

Tathmini$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx.$ State kama yasiyofaa muhimu converges au diverges.

Suluhisho

Anza kwa kugawanya muhimu:

$$\int ^{+∞}_{−∞}xe^x\,dx=\int ^0_{−∞}xe^x\,dx+\int ^{+∞}_0xe^x\,dx. \nonumber$$

Ikiwa ama$\displaystyle \int ^0_{−∞}xe^x\,dx$ au$\displaystyle \int ^{+∞}_0xe^x\,dx$ hupungua, basi$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx$ hupungua. Compute kila muhimu tofauti. Kwa maana ya kwanza,

$\displaystyle \int ^0_{−∞}xe^x\,dx=\lim_{t→−∞}\int ^0_txe^x\,dx$Andika upya kama kikomo.

$=\lim_{t→−∞}(xe^x−e^x)∣^0_t$Matumizi ya ushirikiano na sehemu ya kupata antiderivative. (Hapa$u=x$ na$dv=e^x$.)

$=\lim_{t→−∞}(−1−te^t+e^t)$Tathmini antiderivative.

$=−1.$

Tathmini kikomo. Kumbuka:$\displaystyle \lim_{t→−∞}te^t$ ni indeterminate ya fomu$0⋅∞$ .Hivyo,$\displaystyle \lim_{t→−∞}te^t=\lim_{t→−∞}\frac{t}{e^{−t}}=\lim_{t→−∞}\frac{−1}{e^{−t}}=\lim_{t→−∞}−e^t=0$ kwa Utawala wa L'Hôpital.

Muhimu wa kwanza usiofaa hujiunga. Kwa maana ya pili,

$\displaystyle \int ^{+∞}_0xe^x\,dx=\lim_{t→+∞}\int ^t_0xe^x\,dx$Andika upya kama kikomo.

$=\lim_{t→+∞}(xe^x−e^x)∣^t_0$Kupata antiderivative.

$=\lim_{t→+∞}(te^t−e^t+1)$Tathmini antiderivative.

$=\lim_{t→+∞}((t−1)e^t+1)$Andika upya. ($te^t−e^t$ni indeterminate.)

$=+∞.$Tathmini kikomo.

Hivyo,$\displaystyle \int ^{+∞}_0xe^x\,dx$ hutofautiana. Kwa kuwa hii muhimu$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx$ hutofautiana, hutofautiana pia.

Zoezi$\PageIndex{1}$

Tathmini$\displaystyle \int ^{+∞}_{−3}e^{−x}\,dx.$ State kama yasiyofaa muhimu converges au diverges.

Kidokezo

$$\int ^{+∞}_{−3}e^{−x}\,dx=\lim_{t→+∞}\int ^t_{−3}e^{−x}\,dx \nonumber$$

Jibu

Ni hujiunga na$e^3.$

Kuunganisha Integrand Discontinuous

Sasa hebu tuchunguze integrals ya kazi zenye discontinuity usio na mwisho katika kipindi ambacho ushirikiano hutokea. Fikiria muhimu ya fomu$\displaystyle \int ^b_af(x)\,dx,$ ambapo$f(x)$ ni kuendelea juu$[a,b)$ na kuacha saa$b$. Kwa kuwa kazi$f(x)$ ni kuendelea juu$[a,t]$ ya maadili yote ya$t$ kuridhisha$a \le t<b$, muhimu$\displaystyle \int ^t_af(x)\,dx$ hufafanuliwa kwa maadili yote hayo ya$t$. Hivyo, ni busara kuzingatia maadili ya$\displaystyle \int ^t_af(x)\,dx$ kama$t$ mbinu$b$ za$a \le t<b$. Hiyo ni, sisi kufafanua$\displaystyle \int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx$, mradi kikomo hiki ipo. Kielelezo$\PageIndex{5}$ unaeleza$\displaystyle \int ^t_af(x)\,dx$ kama maeneo ya mikoa kwa ajili ya maadili ya$t$ inakaribia$b$.

Kielelezo$\PageIndex{5}$: Kama inakaribia b kutoka upande wa kushoto, thamani ya eneo kutoka a hadi t inakaribia eneo kutoka a hadi b.

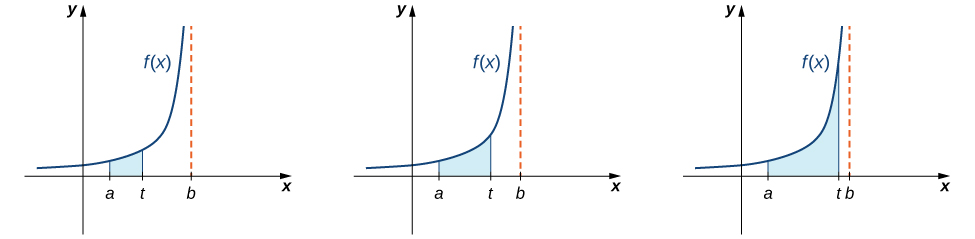
Tunatumia mbinu sawa na kufafanua$\displaystyle \int ^b_af(x)\,dx$, ambapo$f(x)$ ni kuendelea tena$(a,b]$ na discontinuous katika$a$. Sasa tunaendelea na ufafanuzi rasmi.

Ufafanuzi: Kubadilisha na kugeuza Integral yasiyofaa

1. Hebu$f(x)$ uendelee kuendelea$[a,b)$. Kisha, $$\int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx. \label{improperundefb}$$
2. Hebu$f(x)$ uendelee kuendelea$(a,b]$. Kisha, $$\int ^b_af(x)\,dx=\lim_{t→a^+}\int ^b_tf(x)\,dx. \label{improperundefa}$$ Katika kila kesi, kama kikomo ipo, basi muhimu yasiyofaa inasemekana kugeuka. Ikiwa kikomo haipo, basi jambo lisilofaa linasemekana kugeuka.
3. Kama$f(x)$ ni kuendelea juu$[a,b]$ isipokuwa katika hatua$c$ katika$(a,b)$, kisha $$\int ^b_af(x)\,dx=\int ^c_af(x)\,dx+\int ^b_cf(x)\,dx,\label{improperundefc}$$ zinazotolewa wote$\displaystyle \int ^c_af(x)\,dx$ na$\displaystyle \int ^b_cf(x)\,dx$ kugeuza. Ikiwa mojawapo ya integrals haya$\displaystyle \int ^b_af(x)\,dx$ yanatofautiana, basi hupungua.

Mifano zifuatazo zinaonyesha matumizi ya ufafanuzi huu.

Mfano$\PageIndex{6}$: Integrating a Discontinuous Integrand

Tathmini$\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx,$ ikiwa inawezekana. Hali kama muhimu hujiunga au hutofautiana.

Suluhisho

kazi$f(x)=\dfrac{1}{\sqrt{4−x}}$ ni kuendelea juu$[0,4)$ na discontinuous saa 4. Kutumia Equation\ ref {improperundefb} kutoka kwa ufafanuzi, uandike upya$\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx$ kama kikomo:

\ (\ displaystyle\ kuanza {align*}\ int ^4_0\ frac {1} {\ sqrt {4,1x}}\, dx &=\ lim_ {t→ 4 ^}\ int ^t_0\ frac {1} {\ sqrt {4,1x}}\, dx\ quad\\ maandishi {Andika upya kama kikomo.}\\ [4pt]
&=\ lim_ {t→ 4 ^} (-1 2\ sqrt {4,1x}) ^t_0\ quad\ maandishi {Pata antiderivative.}\\ [4pt]
&=\ lim_ {t → 4 ^}} (—2\ sqrt {4,1t} +4)\ quad\ Nakala {Tathmini antiderivative.}\\ [4pt]
&=4. \ quad\ maandishi {Tathmini kikomo.} \ mwisho {align*}\)

Muhimu usiofaa hujiunga.

Mfano$\PageIndex{7}$: Integrating a Discontinuous Integrand

Tathmini$\displaystyle \int ^2_0x\ln x\,dx.$ State kama converges muhimu au diverges.

Suluhisho

Kwa kuwa$f(x)=x\ln x$ ni kuendelea tena$(0,2]$ na ni discontinuous katika sifuri, tunaweza kuandika upya muhimu katika fomu kikomo kwa kutumia Equation\ ref {improperundefa}:

\ (\ displaystyle\ kuanza {align*}\ int ^2_0x\ ln x\, dx &=\ lim_ {t → 0 ^ +}\ int ^2_tx\ ln x\, dx\ quad\ maandishi {Andika upya kama kikomo.}\\ [4pt]
&=\ lim_ {t → 0 ^ +} (\ frac {1} {2} x ^ 2]\ ln x\ frac {1} {4} x ^ 2) ^ 2_t\ quad\ maandishi {Tathmini}\;\ int x\ ln x\, dx\;\ maandishi {kutumia ushirikiano na sehemu na}\; u=\ ln x\;\ maandishi {na}\; dv=x. \\ [4pt]
&=\ lim_ {t→ 0 ^+} (2\ ln 2,1-1-\ frac {1} {2} t^2\ ln t+\ frac {1} {4} t ^ 2). \ quad\ maandishi {Tathmini antiderivative.}\\ [4pt]
&=2\ ln 2,1-1. \ quad\ maandishi {Tathmini kikomo.} \ mwisho {align*}\)

Kwa hiyo

$\displaystyle \lim_{t→0^+}t^2\ln t\;\text{is indeterminate.}$

Ili kuitathmini, andika upya kama quotient na kutumia utawala wa L'Hôpital.

Muhimu usiofaa hujiunga.

Mfano$\PageIndex{8}$: Integrating a Discontinuous Integrand

Tathmini$\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx.$ State kama yasiyofaa muhimu converges au diverges.

Suluhisho

Kwa kuwa$f(x)=1/x^3$ ni discontinuous katika sifuri, kwa kutumia Equation\ ref {improperundefc}, tunaweza kuandika

$$\int ^1_{−1}\frac{1}{x^3}\,dx=\int ^0_{−1}\frac{1}{x^3}\,dx+\int ^1_0\frac{1}{x^3}\,dx.\nonumber$$

Ikiwa mojawapo ya integrals mbili hutofautiana, basi sehemu ya awali inatofautiana. Anza na$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$:

$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx=\lim_{t→0^−}\int ^t_{−1}\frac{1}{x^3}\,dx$Andika upya kama kikomo.

$=\lim_{t→0^−}(−\frac{1}{2x^2})∣^t_{−1}$Kupata antiderivative.

$=\lim_{t→0^−}(−\frac{1}{2t^2}+\frac{1}{2})$Tathmini antiderivative.

$=+∞.$Tathmini kikomo.

Kwa hiyo,$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$ hutofautiana. Tangu$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$ hutofautiana,$\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx$ hutofautiana.

Zoezi$\PageIndex{2}$

Tathmini$\displaystyle \int ^2_0\frac{1}{x}\,dx.$ State kama converges muhimu au diverges.

Kidokezo

Andika$\displaystyle \int ^2_0\frac{1}{x}\,dx$ katika fomu ya kikomo kwa kutumia Equation\ ref {improperundefa}.

Jibu

$+∞$, Ni diverges.

Theorem ya kulinganisha

Si rahisi kila wakati au hata inawezekana kutathmini muhimu isiyofaa moja kwa moja; hata hivyo, kwa kulinganisha na mwingine muhimu waliochaguliwa kwa makini, inaweza kuwa inawezekana kuamua muunganiko wake au tofauti. Ili kuona hili, fikiria kazi mbili zinazoendelea$f(x)$ na$g(x)$ kuridhisha$0≤f(x)≤g(x)$$x≥a$ (Kielelezo$\PageIndex{6}$). Katika kesi hii, tunaweza kuona integrals ya kazi hizi juu ya vipindi vya fomu$[a,t]$ kama maeneo, hivyo tuna uhusiano

$$0≤\int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx \nonumber$$

kwa$t≥a$.

Kielelezo$\PageIndex{6}$: Kama$0≤f(x)≤g(x)$ kwa$x≥a$, basi kwa$t≥a$,$\displaystyle \int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx.$

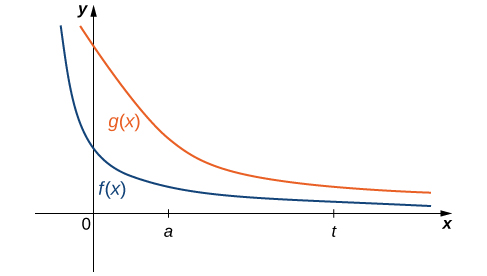
Hivyo, kama

$$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber$$

basi

$$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞ \nonumber$$

pia. Hiyo ni, ikiwa eneo la kanda kati ya grafu ya$f(x)$ na$x$$[a,+∞)$ -axis juu haipatikani, basi eneo la kanda kati ya grafu ya$g(x)$ na$x$$[a,+∞)$ -axis juu haipatikani pia.

Kwa upande mwingine, kama

$$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L \nonumber$$

kwa idadi fulani halisi$L$, basi

$$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx \nonumber$$

lazima hujiunga na thamani ya baadhi ya chini au sawa na$L$, tangu$\displaystyle \int ^t_af(x)\,dx$ kuongezeka kama$t$ ongezeko na$\displaystyle \int ^t_af(x)\,dx≤L$ kwa wote$t≥a.$

Ikiwa eneo la kanda kati ya grafu ya$g(x)$ na$x$ -axis juu$[a,+∞)$ ni ya mwisho, basi eneo la kanda kati ya grafu ya$f(x)$ na$x$ -axis juu pia$[a,+∞)$ ni ya mwisho.

Hitimisho hizi ni muhtasari katika theorem ifuatayo.

Theorem ya kulinganisha

Hebu$f(x)$ na$g(x)$ kuendelea juu ya$[a,+∞).$ kudhani kwamba$0≤f(x)≤g(x)$ kwa$x≥a.$

1. Kama $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber$$ basi $$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞. \nonumber$$
2. Ikiwa$L$ ni $$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L, \nonumber$$ wapi namba halisi, basi $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=M \nonumber$$ kwa idadi halisi$M≤L.$

Mfano$\PageIndex{9}$: Applying the Comparison Theorem

Tumia kulinganisha ili kuonyesha kwamba

$$\int ^{+∞}_1\frac{1}{xe^x}\,dx \nonumber$$

hukutana.

Suluhisho

Tunaweza kuona kwamba

$$0≤\frac{1}{xe^x}≤\frac{1}{e^x}=e^{−x}, \nonumber$$

hivyo kama$\displaystyle \int ^{+∞}_1e^{−x}\,dx$ converges, basi hivyo$\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx$. Kutathmini$\displaystyle \int ^{+∞}_1e^{−x}\,dx,$ kwanza kuandika upya kama kikomo:

$\displaystyle \int ^{+∞}_1e^{−x}\,dx=\lim_{t→+∞}\int ^t_1e^{−x}\,dx$

$=\lim_{t→+∞}(−e^{−x})∣^t_1$

$=\lim_{t→+∞}(−e^{−t}+e^{-1})$

$=e^{-1}.$

Tangu$\displaystyle \int ^{+∞}_1e^{−x}\,dx$ converges, hivyo haina$\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx.$

Mfano$\PageIndex{10}$: Applying the Comparison Theorem

Tumia theorem ya kulinganisha ili kuonyesha kwamba$\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx$ hutofautiana kwa wote$p<1$.

Suluhisho

Kwa$p<1, 1/x≤1/(x^p)$ zaidi ya$[1,+∞).$ Katika Mfano$\PageIndex{1}$, sisi ilionyesha kuwa$\displaystyle \int ^{+∞}_1\frac{1}{x}\,dx=+∞.$ Kwa hiyo,$\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx$ diverges kwa ajili ya wote$p<1$.

Zoezi$\PageIndex{3}$

Tumia kulinganisha ili kuonyesha kwamba$\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx$ hupungua.

Kidokezo

$\frac{1}{x}≤\frac{\ln x}{x}$juu$[e,+∞)$

Jibu

Tangu$\displaystyle \int ^{+∞}_e\frac{1}{x}\,dx=+∞,$$\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx$ hutofautiana.

Laplace inabadilisha

Katika sura chache zilizopita, tumeangalia njia kadhaa za kutumia ushirikiano wa kutatua matatizo halisi ya ulimwengu. Kwa ajili ya mradi huu ujao, sisi ni kwenda kuchunguza maombi ya juu zaidi ya ushirikiano: mabadiliko muhimu. Hasa, tunaelezea kubadilisha Laplace na baadhi ya mali zake. Kubadilisha Laplace hutumiwa katika uhandisi na fizikia ili kurahisisha hesabu zinazohitajika ili kutatua matatizo fulani. Inachukua kazi zilizoelezwa kwa muda na kuzibadilisha kwa kazi zilizoelezwa kwa suala la mzunguko. Inageuka kuwa, mara nyingi, hesabu zinahitajika kutatua matatizo katika uwanja wa mzunguko ni rahisi zaidi kuliko yale yanayotakiwa wakati wa kikoa.

Kubadilisha Laplace hufafanuliwa kwa suala la muhimu kama

$$L{f(t)}=F(s)=\int ^∞_0e^{−st}f(t)dt. \nonumber$$

Kumbuka kuwa pembejeo ya kubadilisha Laplace ni kazi ya muda,$f(t),$ na pato ni kazi ya mzunguko,$F(s)$. Ingawa mifano mingi ya ulimwengu halisi inahitaji matumizi ya namba tata (inayohusisha idadi ya kufikiri$i=\sqrt{−1}),$ katika mradi huu tunajiweka kikomo kwa kazi za namba halisi.

Hebu tuanze na mfano rahisi. Hapa tunahesabu kubadilisha Laplace ya$f(t)=t$. Tuna

$$L{t}=\int ^∞_0te^{−st}dt. \nonumber$$

Hii ni muhimu yasiyofaa, hivyo sisi kueleza katika suala la kikomo, ambayo inatoa

$$L{t}=\int ^∞_0te^{−st}dt=\lim_{z→∞}\int ^z_0te^{−st}dt. \nonumber$$

Sasa tunatumia ushirikiano na sehemu ili kutathmini muhimu. Kumbuka kwamba sisi ni kuunganisha kwa heshima na t, hivyo sisi kutibu s variable kama mara kwa mara. Tuna

$u=t$$du=dt$$dv=e^{−st}dt$$v=−\frac{1}{s}e^{−st}$.

Kisha sisi kupata

$$\begin{align*} \lim_{z→∞}\int ^z_0te^{−st}dt =\lim_{z→∞}[[−\frac{t}{s}e^{−st}]∣^z_0+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+\frac{0}{s}e^{−0s}]+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+0]−\frac{1}{s}[\frac{e^{−st}}{s}]∣^z_0] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}]−\frac{1}{s^2}[e^{−sz}−1]] \\[4pt]\ =\lim_{z→∞}[−\frac{z}{se^{sz}}]−\lim_{z→∞}[\frac{1}{s^2e^{sz}}]+\lim_{z→∞}\frac{1}{s^2} \\[4pt]\ =0−0+\frac{1}{s^2} \\[4pt]\ =\frac{1}{s^2}. \end{align*}$$

1. Tumia mabadiliko ya Laplace ya$f(t)=1.$
2. Tumia mabadiliko ya Laplace ya$f(t)=e^{−3t}.$
3. Mahesabu Laplace kubadilisha ya$f(t)=t^2$. (Kumbuka, utahitaji kuunganisha na sehemu mara mbili.)

Mabadiliko ya Laplace mara nyingi hutumiwa kutatua equations tofauti. Equations tofauti hazifunikwa kwa undani mpaka baadaye katika kitabu hiki; lakini, kwa sasa, hebu tuangalie uhusiano kati ya kubadilisha Laplace ya kazi na kubadilisha Laplace ya derivative yake.

Hebu tuanze na ufafanuzi wa kubadilisha Laplace. Tuna

$$L{f(t)}=\int ^∞_0e^{−st}f(t)dt=\lim_{z→∞}\int ^z_0e^{−st}f(t)dt. \nonumber$$

Tumia ushirikiano na sehemu ili kutathmini$\displaystyle \lim_{z→∞}\int ^z_0e^{−st}f(t)dt$. (Hebu$u=f(t)$ na$dv=e^{−st}dt$.)

Baada ya kuunganisha na sehemu na kutathmini kikomo, unapaswa kuona kwamba

$$L{f(t)}=\frac{f(0)}{s}+\frac{1}{s}[L{f′(t)}]. \nonumber$$

Kisha,

$$L{f′(t)}=sL{f(t)}−f(0). \nonumber$$

Hivyo, tofauti katika uwanja wa wakati unasisitiza kuzidisha kwa s katika uwanja wa mzunguko.

Jambo la mwisho tunaloangalia katika mradi huu ni jinsi Laplace inabadilika$f(t)$ na antiderivative yake yanahusiana. Basi$g(t)=\int ^t_0f(u)du.$ basi,

$$L{g(t)}=\int ^∞_0e^{−st}g(t)dt=\lim_{z→∞}\int ^z_0e^{−st}g(t)dt. \nonumber$$

Tumia ushirikiano na sehemu ya kutathmini$\displaystyle \lim_{z→∞}\int ^z_0e^{−st}g(t)dt.$ (Hebu$u=g(t)$ na$dv=e^{−st}dt$. Kumbuka, kwa njia ambayo tumeelezea$g(t), du=f(t)dt.$)

Kama unaweza kutarajia, unapaswa kuona kwamba

$$L{g(t)}=\frac{1}{s}⋅L{f(t)}. \nonumber$$

Ushirikiano katika uwanja wa wakati unafungua kwa mgawanyiko na$s$ katika uwanja wa mzunguko.

Dhana muhimu

• Integrals ya kazi juu ya vipindi usio na kipimo hufafanuliwa kwa suala la mipaka.
• Integrals ya kazi juu ya muda ambayo kazi ina discontinuity katika mwisho inaweza kuelezwa katika suala la mipaka.
• Kuunganishwa au tofauti ya muhimu isiyofaa inaweza kuamua kwa kulinganisha na thamani ya muhimu isiyofaa ambayo muunganiko au tofauti hujulikana.

Mlinganyo muhimu

• Integrals yasiyofaa

$\displaystyle \int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx$

$\displaystyle \int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx$

$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx$

faharasa

yasiyofaa muhimu

muhimu juu ya muda usio na kipimo au muhimu ya kazi iliyo na kutokuwepo kwa usio juu ya muda; muhimu isiyofaa inaelezwa kwa suala la kikomo. Muhimu usiofaa hujiunga ikiwa kikomo hiki ni nambari halisi ya mwisho; vinginevyo, sehemu isiyofaa inatofautiana