7.6: Ushirikiano wa namba
- Page ID
- 178849
- Takriban thamani ya muhimu ya uhakika kwa kutumia sheria za midpoint na trapezoidal.
- Kuamua hitilafu kabisa na jamaa katika kutumia mbinu ya ushirikiano wa namba.
- Tathmini kosa kamili na jamaa kwa kutumia formula iliyofungwa na hitilafu.
- Kutambua wakati midpoint na trapezoidal sheria juu- au underestimate thamani ya kweli ya muhimu.
- Matumizi utawala Simpson ya takriban thamani ya muhimu uhakika kwa usahihi fulani.
Antiderivatives ya kazi nyingi ama haiwezi kuelezwa au haiwezi kuelezwa kwa urahisi katika fomu iliyofungwa (yaani, kwa suala la kazi zinazojulikana). Kwa hiyo, badala ya kutathmini integrals uhakika wa kazi hizi moja kwa moja, sisi mapumziko kwa mbinu mbalimbali za ushirikiano namba kwa takriban maadili yao. Katika sehemu hii, sisi kuchunguza kadhaa ya mbinu hizi. Kwa kuongeza, tunachunguza mchakato wa kukadiria kosa katika kutumia mbinu hizi.
Utawala wa midpoint
Mapema katika maandishi haya sisi defined muhimu uhakika wa kazi zaidi ya muda kama kikomo cha Riemann kiasi. Kwa ujumla, yoyote jumla Riemann ya kazi\( f(x)\) juu ya muda\([a,b]\) inaweza kutazamwa kama makadirio ya\(\displaystyle ∫^b_af(x)\,dx\). Kumbuka kwamba jumla ya Riemann ya kazi\( f(x)\) zaidi ya muda\( [a,b]\) hupatikana kwa kuchagua kizigeu
\[ P=\{x_0,x_1,x_2,…,x_n\} \nonumber \]
wapi\(\quad a=x_0<x_1<x_2<⋯<x_n=b \)
na seti
\[ S=\{x^*_1,x^*_2,…,x^*_n\} \nonumber \]
wapi\(x_{i−1}≤x^*_i≤x_i \quad \text{for all} \, i.\)
Jumla ya Riemann inayolingana\(P\) na ugawaji na kuweka\(S\) hutolewa na\(\displaystyle \sum^n_{i=1}f(x^*_i)Δx_i\), ambapo urefu\( Δx_i=x_i−x_{i−1},\) wa\( i^{\text{th}}\) subinterval.
Utawala wa midpoint kwa kukadiria muhimu ya uhakika inatumia jumla ya Riemann na subspintervations ya upana sawa na midpoints\( m_i\),, ya kila subinterval badala ya\( x^*_i\). Rasmi, tunasema theorem kuhusu kuunganishwa kwa utawala wa midpoint kama ifuatavyo.
Kudhani kwamba\( f(x)\) ni kuendelea juu ya\([a,b]\). Hebu\( n\) kuwa integer chanya na\( Δx=\dfrac{b−a}{n}\). Ikiwa\( [a,b]\)\( n\) imegawanywa katika sehemu ndogo, kila urefu\( Δx\), na\( m_i\) ni midpoint ya\( i^{\text{th}}\) subinterval, kuweka
\[M_n=\sum_{i=1}^nf(m_i)Δx. \nonumber \]
Kisha\(\displaystyle \lim_{n→∞}M_n=∫^b_af(x)\,dx.\)
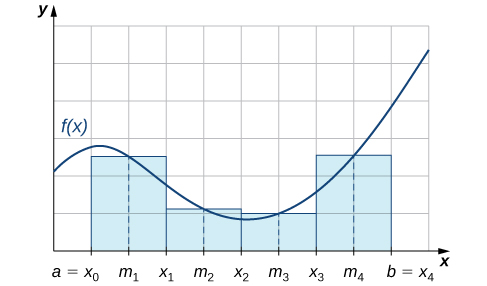
Kama tunaweza kuona katika Kielelezo\(\PageIndex{1}\), ikiwa\( f(x)≥0\) juu\( [a,b]\), basi\(\displaystyle \sum^n_{i=1}f(m_i)Δx\) inalingana na jumla ya maeneo ya rectangles inakaribia eneo kati ya grafu ya\( f(x)\) na\(x\) -axis juu\([a,b]\). Grafu inaonyesha rectangles sambamba na\(M_4\) kwa kazi isiyo ya hasi juu ya muda uliofungwa.\([a,b].\)
Tumia utawala wa midpoint ili ukadirie\(\displaystyle ∫^1_0x^2\,dx\) kutumia vipindi vinne. Linganisha matokeo na thamani halisi ya hii muhimu.
Solution: Kila subinterval ina urefu\( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Kwa hiyo, subintervants inajumuisha
\[\left[0,\tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2},\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].\nonumber \]
midpoints ya subinternations hizi ni\(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right\}.\) Hivyo,
\[\begin{align*} M_4 &=\frac{1}{4}\cdot f\left(\frac{1}{8}\right)+\frac{1}{4}\cdot f\left(\frac{3}{8}\right)+\frac{1}{4}\cdot f\left(\frac{5}{8}\right)+\frac{1}{4}\cdot f\left(\frac{7}{8}\right) \\[4pt] &=\frac{1}{4}⋅\frac{1}{64}+\frac{1}{4}⋅\frac{9}{64}+\frac{1}{4}⋅\frac{25}{64}+\frac{1}{4}⋅\frac{49}{64}\\[4pt] &=\frac{21}{64} = 0.328125. \end{align*}\]
Tangu
\[ ∫^1_0x^2\,dx=\frac{1}{3},\nonumber \]
makosa kabisa katika makadirio hii ni:
\[\left\lvert\dfrac{1}{3}−\dfrac{21}{64}\right\rvert=\dfrac{1}{192}≈0.0052, \nonumber \]
na tunaona kwamba utawala wa midpoint hutoa makadirio ambayo ni karibu na thamani halisi ya muhimu ya uhakika.
Tumia\(M_6\) ili kukadiria urefu wa pembe\(y=\frac{1}{2}x^2\)\([1,4]\).
Suluhisho: urefu wa\(y=\frac{1}{2}x^2\) juu\([1,4]\) ni
\[s = ∫^4_1\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx.\nonumber \]
Tangu\(\dfrac{dy}{dx}=x\), hii muhimu inakuwa\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx.\)
Ikiwa\([1,4]\) imegawanywa katika vipindi sita, basi kila subinterval ina urefu\(Δx=\dfrac{4−1}{6}=\dfrac{1}{2}\) na midpoints ya subspintervals ni\(\left\{\frac{5}{4},\frac{7}{4},\frac{9}{4},\frac{11}{4},\frac{13}{4},\frac{15}{4}\right\}\). Kama sisi kuweka\(f(x)=\sqrt{1+x^2}\),
\[\begin{align*} M_6 &=\tfrac{1}{2}\cdot f\left(\frac{5}{4}\right)+\tfrac{1}{2}\cdot f\left(\frac{7}{4}\right)+\frac{1}{2}\cdot f\left(\frac{9}{4}\right)+\frac{1}{2}\cdot f\left(\frac{11}{4}\right)+\frac{1}{2}\cdot f\left(\frac{13}{4}\right)+\frac{1}{2}\cdot f\left(\frac{15}{4}\right) \\[4pt] &≈\frac{1}{2}(1.6008+2.0156+2.4622+2.9262+3.4004+3.8810)=8.1431 \, \text{ units}. \end{align*}\]
Tumia utawala wa midpoint na\( n=2\) kukadiria\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Kidokezo
-
\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)
- Jibu
-
\(\dfrac{24}{35}\approx 0.685714\)
Utawala wa Trapezoidal
Tunaweza pia takriban thamani ya muhimu kwa kutumia trapezoids badala ya rectangles. Katika Kielelezo\(\PageIndex{2}\), eneo chini ya Curve ni takriban na trapezoids badala ya rectangles.
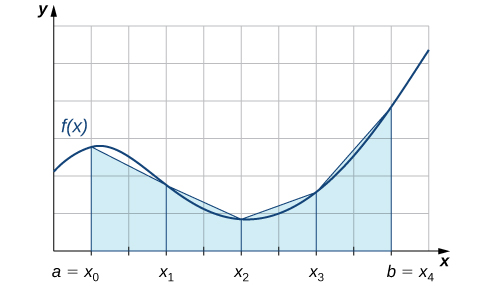
Utawala wa trapezoidal kwa kukadiria integrals uhakika hutumia trapezoids badala ya rectangles kwa takriban eneo chini ya curve. Ili kupata ufahamu katika fomu ya mwisho ya utawala, fikiria trapezoids iliyoonyeshwa kwenye Kielelezo\(\PageIndex{2}\). Tunadhani kwamba urefu wa kila subinterval hutolewa na\(Δx\). Kwanza, kumbuka kwamba eneo la trapezoid yenye urefu\(h\) na msingi wa urefu\(b_1\) na\(b_2\) hutolewa na\(\text{Area}=\frac{1}{2}h(b_1+b_2)\). Tunaona kwamba trapezoid ya kwanza ina urefu\(Δx\) na sambamba besi za urefu\( f(x_0)\) na\( f(x_1)\). Hivyo, eneo la trapezoid kwanza katika Kielelezo\(\PageIndex{2}\) ni
\[ \frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big).\nonumber \]
Sehemu za trapezoids tatu zilizobaki ni
\(\dfrac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big),\, \dfrac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big),\)na\( \dfrac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\)
Kwa hiyo,
\[∫^b_af(x)\,dx≈\frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big)+\frac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big)+\frac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big)+\frac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\nonumber \]
Baada ya kuchukua sababu ya kawaida ya\(\frac{1}{2}Δx\) na kuchanganya kama maneno, tuna
\[ ∫^b_af(x)\,dx≈\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f(x_4)\Big].\nonumber \]
Kuzalisha, tunasema rasmi utawala wafuatayo.
Kudhani kwamba\(f(x)\) ni kuendelea juu ya\([a,b]\). Hebu\(n\) kuwa integer chanya na\(Δx=\dfrac{b−a}{n}\). Hebu\( [a,b]\)\(n\) kugawanywa katika sehemu ndogo\(Δx\), kila urefu, na mwisho\( P=\{x_0,x_1,x_2…,x_n\}.\)
Kuweka
\[T_n=\frac{Δx}{2}\Big[f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Kisha,\(\displaystyle \lim_{n→+∞}T_n=∫^b_af(x)\,dx.\)
Kabla ya kuendelea, hebu tufanye uchunguzi machache kuhusu utawala wa trapezoidal. Kwanza kabisa, ni muhimu kutambua kwamba
\(T_n=\dfrac{1}{2}(L_n+R_n)\)wapi\(\displaystyle L_n=\sum_{i=1}^nf(x_{i−1})Δx\) na\(\displaystyle R_n=\sum_{i=1}^nf(x_i)Δx.\)
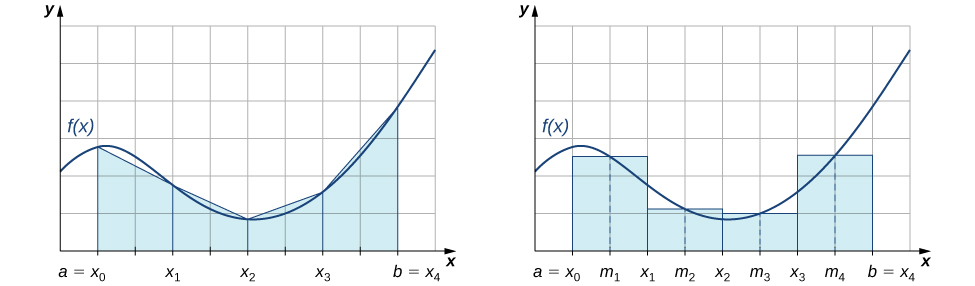
Hiyo ni,\(L_n\) na\(R_n\) takriban muhimu kwa kutumia mwisho wa mkono wa kushoto na wa kulia wa kila subinterval, kwa mtiririko huo. Aidha, uchunguzi wa makini wa Kielelezo\(\PageIndex{3}\) hutuongoza kufanya uchunguzi wafuatayo kuhusu kutumia sheria za trapezoidal na sheria za midpoint ili kukadiria muhimu ya kazi isiyo ya kawaida. Utawala wa trapezoidal huelekea kuzingatia thamani ya muhimu ya uhakika kwa utaratibu juu ya vipindi ambapo kazi ni concave juu na underestimate thamani ya muhimu ya uhakika kwa utaratibu juu ya vipindi ambapo kazi ni concave chini. Kwa upande mwingine, utawala wa midpoint huelekea wastani wa makosa haya kwa kiasi fulani kwa kuzingatia sehemu na kupunguza kiasi cha thamani ya muhimu ya uhakika juu ya aina hizi za vipindi. Hii inatuongoza kufikiri kwamba, kwa ujumla, utawala wa midpoint huelekea kuwa sahihi zaidi kuliko utawala wa trapezoidal.
Tumia utawala wa trapezoidal kukadiria\(\displaystyle ∫^1_0x^2\,dx\) kutumia subinternations nne.
Suluhisho
Mwisho wa vipindi vinajumuisha vipengele vya kuweka\(P=\left\{0,\frac{1}{4},\, \frac{1}{2},\, \frac{3}{4},1\right\}\) na\(Δx=\frac{1−0}{4}=\frac{1}{4}.\) hivyo,
\ [kuanza {align*} ^1_0x^2dx &≈\ Frac {1} {2}}\ Frac {1}\ Frac {1} {4}\ Big [f (0) +2\, f\ kushoto (\ tfrac {1} {1} {1}\ haki) +2\, f\ kushoto (\ tfrac {3} {4}\ haki) +f (1)\ Big]\\ [4pt]
&=\ tfrac {1} {8}\ kubwa (0+2\ tfrac {1} {16} +2\ tfrac {1} {4} +2\ tfrac {9} {16} +1\ big)\\[4pt] &=\frac{11}{32} = 0.34375\end{align*}\]
Tumia utawala wa trapezoidal na\( n=2\) kukadiria\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Kidokezo
-
Weka\(Δx=\dfrac{1}{2}.\) Mwisho wa vipindi ni vipengele vya kuweka\(P=\left\{1,\frac{3}{2},2\right\}.\)
- Jibu
-
\(\dfrac{17}{24} \approx 0.708333\)
Hitilafu kamili na ya Jamaa
Kipengele muhimu cha kutumia sheria hizi za makadirio ya namba lina kuhesabu kosa katika kuitumia kwa kukadiria thamani ya muhimu ya uhakika. Sisi kwanza tunahitaji kufafanua kosa kamili na kosa la jamaa.
Ikiwa\(B\) ni makadirio yetu ya kiasi fulani kuwa na thamani halisi ya\(A\), basi kosa kabisa linatolewa na\(|A−B|\).
Hitilafu ya jamaa ni kosa kama asilimia ya thamani halisi na hutolewa na\[\left\lvert\frac{A−B}{A}\right\rvert⋅100\%. \nonumber \]
Tumia hitilafu kamili na ya jamaa katika makadirio ya\(\displaystyle ∫^1_0x^2\,dx\) kutumia utawala wa midpoint, uliopatikana katika Mfano\(\PageIndex{1}\).
Suluhisho: Thamani ya mahesabu ni\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) na makadirio yetu kutoka kwa mfano ni\(M_4=\frac{21}{64}\). Hivyo, kosa kabisa linatolewa na\(\left\lvert\frac{1}{3}−\frac{21}{64}\right\rvert=\frac{1}{192}≈0.0052.\)
Hitilafu ya jamaa ni\[\frac{1/192}{1/3}=\frac{1}{64}≈0.015625≈1.6\%.\nonumber \]
Tumia hitilafu kamili na ya jamaa katika makadirio ya\(\displaystyle ∫^1_0x^2\,dx\) kutumia utawala wa trapezoidal, uliopatikana katika Mfano\(\PageIndex{3}\).
Suluhisho: Thamani ya mahesabu ni\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) na makadirio yetu kutoka kwa mfano ni\(T_4=\frac{11}{32}\). Hivyo, kosa kabisa linatolewa na\(\left\lvert\frac{1}{3}−\frac{11}{32}\right\rvert=\frac{1}{96}≈0.0104.\)
Hitilafu ya jamaa hutolewa na\[\frac{1/96}{1/3}=0.03125≈3.1\%.\nonumber \]
Katika checkpoint mapema, sisi inakadiriwa\(\displaystyle ∫^2_1\frac{1}{x}\,dx\) kuwa\(\frac{24}{35}\) kutumia\(M_2\). Thamani halisi ya muhimu hii ni\(\ln 2\). Kutumia\(\frac{24}{35}≈0.6857\) na\(\ln 2≈0.6931,\) kuhesabu kosa kamili na kosa la jamaa.
- Kidokezo
-
Tumia mifano ya awali kama mwongozo.
- Jibu
-
hitilafu kamili\(\approx 0.0074,\) na hitilafu ya jamaa\(\approx 1.1\%\)
Hitilafu mipaka kwenye Kanuni za Midpoint na Trapezoidal
Katika mifano miwili iliyopita, tuliweza kulinganisha makadirio yetu ya muhimu na thamani halisi ya muhimu; hata hivyo, hatuwezi kuwa na anasa hii. Kwa ujumla, kama sisi ni makadirio muhimu, sisi ni kufanya hivyo kwa sababu hatuwezi kukokotoa thamani halisi ya muhimu yenyewe kwa urahisi. Kwa hiyo, mara nyingi husaidia kuwa na uwezo wa kuamua juu amefungwa kwa makosa katika makadirio ya muhimu. Theorem ifuatayo hutoa mipaka ya makosa kwa sheria za midpoint na trapezoidal. Theorem inasemwa bila ushahidi.
Hebu\(f(x)\) kuwa kazi ya kuendelea juu\([a,b]\), kuwa na derivative ya pili\(f''(x)\) juu ya muda huu. Ikiwa\(M\) ni thamani ya juu ya\(|f''(x)|\) juu\([a,b]\), basi mipaka ya juu ya kosa katika kutumia\(M_n\) na\(T_n\) kukadiria\(\displaystyle ∫^b_af(x)\,dx\) ni
\[\text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}\label{MidError} \]
na
\[\text{Error in}\, T_n≤\frac{M(b−a)^3}{12n^2} \nonumber \].
Tunaweza kutumia mipaka hii kuamua thamani ya\(n\) muhimu ili kuhakikisha kuwa kosa katika makadirio ni chini ya thamani maalum.
Ni thamani gani ya\(n\) lazima kutumika kuhakikisha kwamba makadirio ya\(\displaystyle ∫^1_0e^{x^2}\,dx\) ni sahihi kwa ndani\(0.01\) kama sisi kutumia midpoint utawala?
Suluhisho
Tunaanza kwa kuamua thamani ya\(M\), thamani ya juu ya\( |f''(x)|\) juu\( [0,1]\) kwa\( f(x)=e^{x^2}\). Tangu\( f′(x)=2xe^{x^2},\) tuna
\[ f''(x)=2e^{x^2}+4x^2e^{x^2}.\nonumber \]
Hivyo,
\[ |f''(x)|=2e^{x^2}(1+2x^2)≤2⋅e⋅3=6e.\nonumber \]
Kutoka kwa Equation iliyofungwa na hitilafu\(\ref{MidError}\), tuna
\[ \text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}≤\frac{6e(1−0)^3}{24n^2}=\frac{6e}{24n^2}.\nonumber \]
Sasa tunatatua usawa wafuatayo kwa\(n\):
\[\frac{6e}{24n^2}≤0.01.\nonumber \]
Hivyo,\(n≥\sqrt{\frac{600e}{24}}≈8.24.\) Tangu\(n\) lazima integer kuridhisha kukosekana kwa usawa huu, uchaguzi wa\(n=9\) bila kuhakikisha kwamba
\[ \left\lvert ∫^1_0e^{x^2}\,dx−M_n \right\rvert <0.01.\nonumber \]
Uchambuzi
Tunaweza kuwa kujaribiwa kwa pande zote\(8.24\) chini na kuchagua\(n=8\), lakini hii itakuwa sahihi kwa sababu ni lazima tuwe na integer kubwa kuliko au sawa na\(8.24\). Tunahitaji kukumbuka kwamba makadirio ya kosa hutoa juu amefungwa tu kwa kosa. makadirio halisi inaweza, kwa kweli, kuwa makadirio bora zaidi kuliko unahitajika kwa makosa amefungwa.
Matumizi Equation\(\ref{MidError}\) kupata juu amefungwa kwa makosa katika\(M_4\) kutumia makisio\(\displaystyle ∫^1_0x^2\,dx.\)
- Kidokezo
-
\(f''(x)=2,\)hivyo\(M=2.\)
- Jibu
-
\(\dfrac{1}{192}\)
Simpson ya utawala
Kwa utawala wa midpoint, tulikadiria maeneo ya mikoa chini ya curves kwa kutumia rectangles. Kwa maana, sisi takriban Curve na kazi piecewise mara kwa mara. Kwa utawala wa trapezoidal, tulifikia curve kwa kutumia kazi za mstari wa kipande. Nini kama tulikuwa, badala yake, kwa takriban Curve kutumia kazi piecewise quadratic? Kwa utawala wa Simpson, tunafanya hili tu. Tunagawanya muda katika idadi hata ya vipindi, kila moja ya upana sawa. Zaidi ya jozi ya kwanza ya subspinternations sisi takriban\(\displaystyle ∫^{x_2}_{x_0}f(x)\,dx\) na\(\displaystyle ∫^{x_2}_{x_0}p(x)\,dx\), ambapo\(p(x)=Ax^2+Bx+C\) ni kazi quadratic kupita kupitia\((x_0,f(x_0)), \,(x_1,f(x_1)),\) na\((x_2,f(x_2))\) (Kielelezo\(\PageIndex{4}\)). Zaidi ya jozi ya pili ya vipindi tunakaribia\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) na muhimu ya kazi nyingine ya quadratic inayopitia\( (x_2,f(x_2)), \,(x_3,f(x_3)),\) na Utaratibu\((x_4,f(x_4)).\) huu unaendelea na kila jozi mfululizo wa subinternations.
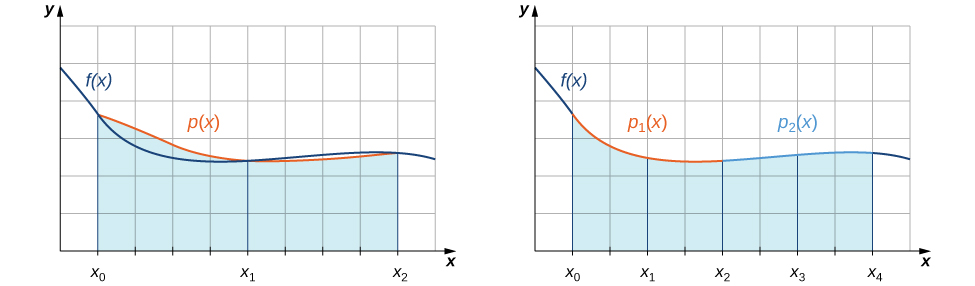
Ili kuelewa formula kwamba sisi kupata kwa utawala Simpson ya, tunaanza kwa deriving formula kwa makadirio hii juu ya subinternations mbili za kwanza. Tunapopitia kupitia derivation, tunahitaji kukumbuka mahusiano yafuatayo:
\[f(x_0)=p(x_0)=Ax_0^2+Bx_0+C \nonumber \]
\[f(x_1)=p(x_1)=Ax_1^2+Bx_1+C \nonumber \]
\[f(x_2)=p(x_2)=Ax_2^2+Bx_2+C \nonumber \]
\(x_2−x_0=2Δx\),\(Δx\) wapi urefu wa subinterval.
\(x_2+x_0=2x_1,\)tangu\(x_1=\dfrac{(x_2+x_0)}{2}\).
Hivyo,
\ [kuanza {align*} ^ {x_2} _ {x_0} f (x)\, dx &≈ ^ {x_2} _ {x_0} p (x)\, dx\\ [4pt]
&=^ {x_2} _ {x_0} (Ax ^ 2+Bx+C)\, dx\\ [4pt]
&=\ kushoto (\ frac {A} {3} x ^ 3+\ Frac {B} {2} X ^ 2+CX\ haki)\ kubwa|^ {x_2} _ {x_0} & &\ maandishi {Kupata antiderivative.}\\ [4pt]
&=\ Frac {A} {3} (x_2^3—x_0^3) +\ frac {B} {2} (x_2^2—x_0 ^ 2) +C (x_2,1x_0) & &\ maandishi {Tathmini antiderivative.}\\ [4pt]
&=\ Frac {A} {3} (x_2,1x_0) (x_2^2^2+x_0+x_0 ^ 2) +\ frac c {B} {2} (x_2—x_0) (x_2+x_0) +C (x_2—x_0)\\ [4pt]
&=\ frac {x_2,1x_0} {6}\ kubwa (2A (x_2^2+x_2+x_0+x_0 ^ 2) +3B (x_2+x__0) +6C\ Bigg) & &\ maandishi {Factor nje}\,\ frac {x_2,1x_0} {6}.\\ [4pt]
&=\ frac {Δx} {3}\ kubwa (Ax_2^2+Bx_2+C) + (Ax_0 ^ 2+Bx_0+C) +A (x_2^2x_2x_0+x_0^2) +2x_0 ^ 2) +2 B (x_2+x_0) +4C\ bigg) & &\ maandishi {Panga upya masharti. Kumbuka:}\ enspace Δx =\ frac {x_2,1x_0} {2}\\ [4pt]
&=\ Frac {Δx} {3}\ kubwa (f (x_2) +f (x_0) +A (x_2+x_0) ^2+2B (x_2+x_0) +4C\ kubwa) & &\ Nakala Factor {na mbadala:}\\ [4pt]
& & &\ quad f (x_2) =Ax_2 ^ 2+Bx_2+C\ enspace\ maandishi {na}\ enspace f (x_0) =Ax_0 ^ 2+Bx_0+C.\\ [4pt]
&=\ frac {Δx} {3}\ kubwa (f (x_2) +f (x_0) +A (2x_1) ^2+2B (2x_1) +4C\ kubwa) & &\ maandishi {mbadala}\, x_2+x_0=2x_1.\\ [4pt] & & &\ quad\ maandishi {Kumbuka:}\, x_0=2x_1.\ [4pt]
& & &\ quad\ maandishi {Kumbuka:}\, x_0=2x_1.\ [4pt] & & &\ quad\ maandishi {Kumbuka:}\, x__1 =\ frac {x_2+x_0} {2}\ enspace\ maandishi {ni midpoint.}\\ [4pt]
&=\ frac {Δx} {3}\ kubwa (f (x_2) +4f (x_1) +f (x_0)\ kubwa). & &\ maandishi {Panua na mbadala}\, f (x_1) =Ax_1^2+Bx_1+C.\ mwisho {align*}\]
Kama sisi takriban\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) kutumia njia hiyo, tunaona kwamba tuna
\[∫^{x_4}_{x_2}f(x)\,dx≈\frac{Δx}{3}(f(x_4)+4\,f(x_3)+f(x_2)).\nonumber \]
Kuchanganya makadirio haya mawili, tunapata
\[∫^{x_4}_{x_0}f(x)\,dx≈\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+f(x_4)).\nonumber \]
mfano inaendelea kama sisi kuongeza jozi ya subinternations kwa makadirio yetu. Utawala wa jumla unaweza kusema kama ifuatavyo.
Kudhani kwamba\(f(x)\) ni kuendelea juu ya\([a,b]\). Hebu\(n\) kuwa chanya hata integer na\(Δx=\dfrac{b−a}{n}\). Hebu\([a,b]\) kugawanywa katika\(n\) subspinternations, kila urefu\(Δx\), na endpoints katika\(P=\{x_0,x_1,x_2,…,x_n\}.\) Set
\[S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Kisha,
\[\lim_{n→+∞}S_n=∫^b_af(x)\,dx.\nonumber \]
Kama vile utawala wa trapezoidal ni wastani wa sheria za mkono wa kushoto na wa kulia kwa kukadiria integrals uhakika, utawala wa Simpson unaweza kupatikana kutoka midpoint na sheria trapezoidal kwa kutumia wastani mizigo. Inaweza kuonyeshwa kuwa\(S_{2n}=\left(\frac{2}{3}\right)M_n+\left(\frac{1}{3}\right)T_n\).
Pia inawezekana kuweka amefungwa juu ya makosa wakati wa kutumia utawala Simpson kwa takriban muhimu uhakika. Waliofungwa katika kosa hutolewa na sheria ifuatayo:
Hebu\(f(x)\) kuwa kazi ya kuendelea juu ya\([a,b]\) kuwa derivative nne,\( f^{(4)}(x)\), juu ya kipindi hiki. Ikiwa\(M\) ni thamani ya juu ya\(∣f^{(4)}(x)∣\) juu\([a,b]\), basi juu ya kufungwa kwa kosa la kutumia kwa\(S_n\) kukadiria\(\displaystyle ∫^b_af(x)\,dx\) hutolewa na
\[\text{Error in}\, S_n≤\frac{M(b−a)^5}{180n^4}. \nonumber \]
Tumia\(S_2\) kwa takriban\(\displaystyle ∫^1_0x^3\,dx\). Tathmini amefungwa kwa makosa katika\(S_2\).
Suluhisho
Tangu\([0,1]\) imegawanywa katika vipindi viwili, kila subinterval ina urefu\(Δx=\frac{1−0}{2}=\frac{1}{2}\). Mwisho wa vipindi hivi ni\(\left\{0,\frac{1}{2},1\right\}\). Kama sisi kuweka\(f(x)=x^3,\) basi
\[S_2=\frac{1}{3}⋅\frac{1}{2}(f(0)+4\,f(\frac{1}{2})+f(1))=\frac{1}{6}(0+4⋅\frac{1}{8}+1)=\frac{1}{4}.\nonumber \]
Tangu\( f^{(4)}(x)=0\) na hivyo\(M=0,\) tunaona kwamba
Hitilafu katika\(S_2≤\frac{0(1)^5}{180⋅2^4}=0.\)
Hii amefungwa inaonyesha kwamba thamani kupatikana kwa njia ya utawala Simpson ni halisi. Angalia haraka kuthibitisha kwamba, kwa kweli,\(\displaystyle ∫^1_0x^3\,dx=\frac{1}{4}.\)
Tumia\(S_6\) kukadiria urefu wa curve\(y=\frac{1}{2}x^2\) juu\([1,4].\)
Suluhisho
Urefu wa\(y=\frac{1}{2}x^2\) juu\([1,4]\) ni\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx\). Ikiwa\([1,4]\) tunagawanyika katika vipindi sita, basi kila subinterval ina urefu\(Δx=\frac{4−1}{6}=\frac{1}{2}\), na mwisho wa vipindi ni\( \left\{1,\frac{3}{2},2,\frac{5}{2},3,\frac{7}{2},4\right\}.\) Kuweka\( f(x)=\sqrt{1+x^2}\),
\[S_6=\frac{1}{3}⋅\frac{1}{2}(f(1)+4f(\frac{3}{2})+2f(2)+4f(\frac{5}{2})+2f(3)+4f(\frac{7}{2})+f(4)).\nonumber \]
Baada ya kubadilisha, tuna
\[S_6=\frac{1}{6}(1.4142+4⋅1.80278+2⋅2.23607+4⋅2.69258+2⋅3.16228+4⋅3.64005+4.12311)≈8.14594\,\text{units}. \nonumber \]
Tumia\(S_2\) kukadiria\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Kidokezo
-
\[S_2=\frac{1}{3}Δx\left(f(x_0)+4f(x_1)+f(x_2)\right) \nonumber \]
- Jibu
-
\(\frac{25}{36} \approx 0.694444\)
Dhana muhimu
- Tunaweza kutumia ushirikiano wa namba ili kukadiria maadili ya integrals ya uhakika wakati fomu imefungwa ya muhimu ni vigumu kupata au wakati thamani ya takriban tu ya muhimu ya uhakika inahitajika.
- Mbinu za kawaida zinazotumiwa kwa ushirikiano wa namba ni utawala wa midpoint, utawala wa trapezoidal, na utawala wa Simpson.
- Utawala wa midpoint unakaribia muhimu kwa kutumia mikoa ya mstatili ambapo utawala wa trapezoidal unakaribia muhimu kwa kutumia makadirio ya trapezoidal.
- utawala Simpson ya approximates muhimu uhakika na kwanza makadirio ya kazi ya awali kwa kutumia kazi piecewise quadratic.
Mlinganyo muhimu
- Utawala wa midpoint
\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\)
- Trapezoidal utawala
\(T_n=\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+⋯+2\,f(x_{n−1})+f(x_n)\Big]\)
- utawala Simpson
\(S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+4\,f(x_5)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]\)
- Hitilafu imefungwa kwa utawala wa midpoint
Hitilafu katika\(M_n≤\dfrac{M(b−a)^3}{24n^2}\), wapi\(M\) thamani ya\(|f''(x)|\) juu ya zaidi\([a,b]\).
- Hitilafu imefungwa kwa utawala wa trapezoidal
Hitilafu katika\(T_n≤\dfrac{M(b−a)^3}{12n^2}\), wapi\(M\) thamani ya\(|f''(x)|\) juu ya zaidi\([a,b]\).
- Hitilafu kufungwa kwa utawala Simpson ya
Hitilafu katika\(S_n≤\dfrac{M(b−a)^5}{180n^4}\), wapi\(M\) thamani ya\(∣f^{(4)}(x)∣\) juu ya zaidi\([a,b]\).
faharasa
- hitilafu kabisa
- ikiwa\(B\) ni makadirio ya kiasi fulani kuwa na thamani halisi ya\(A\), basi kosa kabisa linatolewa na\( |A−B|\)
- utawala wa katikati
- sheria ambayo inatumia jumla ya Riemann ya fomu\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\), wapi\( m_i\) midpoint ya\(i^{\text{th}}\) subinterval kwa takriban\(\displaystyle ∫^b_af(x)\,dx\)
- ushirikiano wa namba
- mbinu mbalimbali za namba zinazotumiwa kukadiria thamani ya muhimu ya uhakika, ikiwa ni pamoja na utawala wa midpoint, utawala wa trapezoidal, na utawala wa Simpson
- kosa la jamaa
- makosa kama asilimia ya thamani halisi, iliyotolewa na\[\text{relative error}=\left|\frac{A−B}{A}\right|⋅100\%\nonumber \]
- utawala Simpson
- sheria ambayo inakaribia\(\displaystyle ∫^b_af(x)\,dx\) kutumia eneo chini ya kazi ya quadratic ya kipande.
\(S_n\)Makadirio\(\displaystyle ∫^b_af(x)\,dx\) ya hutolewa na\[S_n=\frac{Δx}{3}\big(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\big).\nonumber \]
- utawala wa trapezoidal
- sheria ambayo inakaribia\(\displaystyle ∫^b_af(x)\,dx\) kutumia eneo la trapezoids.
\(T_n\)Makadirio\(\displaystyle ∫^b_af(x)\,dx\) ya hutolewa na\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\big).\nonumber \]
Wachangiaji na Majina
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College). Notes added to development of area under a parabola and typos fixed in original text.


