6.9: Calculus ya Kazi za Hyperbolic

Last updated
Save as PDF

Page ID: 178255

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Tumia fomu za derivatives na integrals ya kazi za hyperbolic.
Tumia formula kwa ajili ya derivatives ya kazi inverse hyperbolic na integrals yao kuhusishwa.
Eleza hali ya kawaida kutumika ya Curve catenary.

Tulianzishwa kwa kazi za hyperbolic hapo awali, pamoja na baadhi ya mali zao za msingi. Katika sehemu hii, tunaangalia tofauti na ushirikiano formula kwa ajili ya kazi hyperbolic na inverses yao.

Derivatives na Integrals ya Kazi Hyperbolic

Kumbuka kwamba sine hyperbolic na cosine hyperbolic hufafanuliwa kama

\[\sinh x=\dfrac{e^x−e^{−x}}{2} \nonumber \]

\[\cosh x=\dfrac{e^x+e^{−x}}{2}. \nonumber \]

Kazi nyingine ya hyperbolic hufafanuliwa kwa suala la\(\sinh x\) na\(\cosh x\). Grafu za kazi za hyperbolic zinaonyeshwa kwenye Kielelezo\(\PageIndex{1}\).

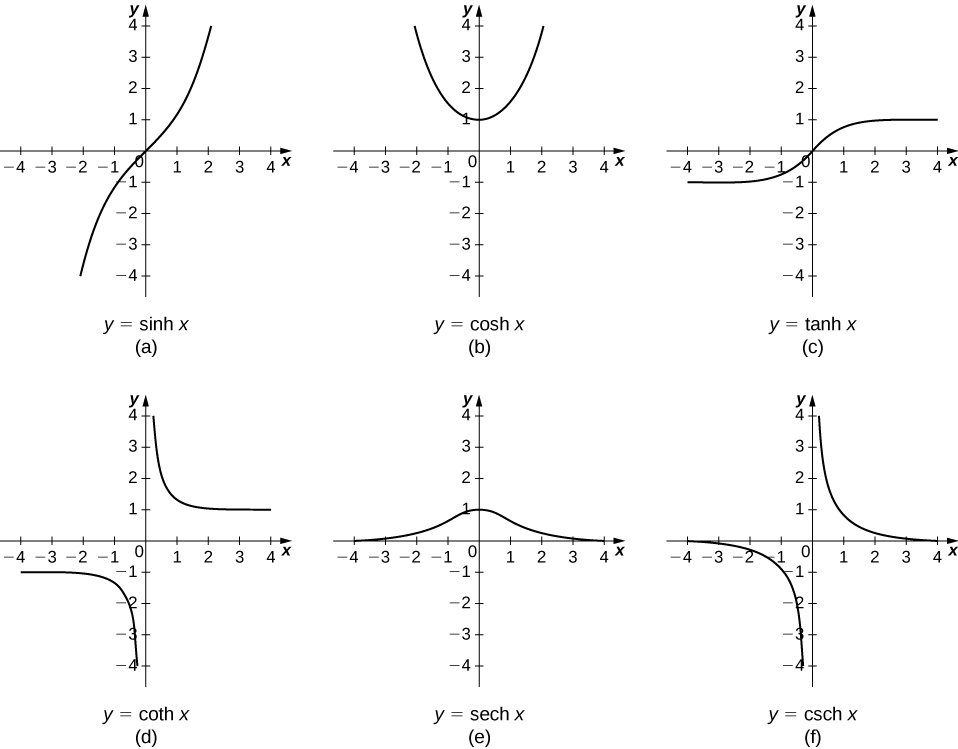
Takwimu hii ina grafu sita. Grafu ya kwanza iliyoandikwa “a” ni ya kazi y=sinh (x). Ni kazi inayoongezeka kutoka kwa roboduara ya 3, kwa njia ya asili hadi quadrant ya kwanza. Grafu ya pili inaitwa “b” na ni ya kazi y=cosh (x). Inapungua katika roboduara ya pili kwa kupinga y=1, halafu inakuwa kazi inayoongezeka. Grafu ya tatu iliyoandikwa “c” ni ya kazi y=tanh (x). Ni kazi inayoongezeka kutoka kwa quadrant ya tatu, kwa njia ya asili, hadi quadrant ya kwanza. Grafu ya nne inaitwa “d” na ni ya kazi y = coth (x). Ina vipande viwili, moja katika quadrant ya tatu na moja katika quadrant ya kwanza yenye asymptote ya wima kwenye mhimili wa y. Grafu ya tano inaitwa “e” na ni ya kazi y=sech (x). Ni curve juu ya x-axis, kuongezeka katika roboduara ya pili, kwa y mhimili katika y=1 na kisha itapungua. Grafu ya sita inaitwa “f” na ni ya kazi y=csch (x). Ina vipande viwili, moja katika quadrant ya tatu na moja katika quadrant ya kwanza yenye asymptote ya wima kwenye mhimili wa y. — Kielelezo\(\PageIndex{1}\): Grafu ya kazi za hyperbolic.

Ni rahisi kuendeleza fomu za kutofautisha kwa kazi za hyperbolic. Kwa mfano, kuangalia\(\sinh x\) tuna

\[\begin{align*} \dfrac{d}{dx} \left(\sinh x \right) &=\dfrac{d}{dx} \left(\dfrac{e^x−e^{−x}}{2}\right) \\[4pt] &=\dfrac{1}{2}\left[\dfrac{d}{dx}(e^x)−\dfrac{d}{dx}(e^{−x})\right] \\[4pt] &=\dfrac{1}{2}[e^x+e^{−x}] \\[4pt] &=\cosh x. \end{align*} \nonumber \]

Vile vile,

\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]

Sisi muhtasari formula tofauti kwa ajili ya kazi hyperbolic katika Jedwali\(\PageIndex{1}\).

Jedwali\(\PageIndex{1}\): Derivatives ya Kazi za Hyperbolic
\(f(x)\)	\(\dfrac{d}{dx}f(x)\)
\ (f (x)\)” style="Nakala-align:center; ">\(\sinh x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:katikati; ">\(\cosh x\)
\ (f (x)\)” style="Nakala-align:center; ">\(\cosh x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:katikati; ">\(\sinh x\)
\ (f (x)\)” style="Nakala-align:center; ">\(\tanh x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:katikati; ">\(\text{sech}^2 \,x\)
\ (f (x)\)” style="Nakala-align:center; ">\(\text{coth } x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:katikati; ">\(−\text{csch}^2\, x\)
\ (f (x)\)” style="Nakala-align:center; ">\(\text{sech } x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:katikati; ">\(−\text{sech}\, x \tanh x\)
\ (f (x)\)” style="Nakala-align:center; ">\(\text{csch } x\)	\ (\ dfrac {d} {dx} f (x)\)” style="text-align:katikati; ">\(−\text{csch}\, x \coth x\)

Hebu tuchukue muda wa kulinganisha derivatives ya kazi za hyperbolic na derivatives ya kazi za kawaida za trigonometric. Kuna mengi ya kufanana, lakini tofauti pia. Kwa mfano, derivatives ya kazi sine mechi:

\[\dfrac{d}{dx} \sin x=\cos x \nonumber \]

\[\dfrac{d}{dx} \sinh x=\cosh x. \nonumber \]

Vipengele vya kazi za cosine, hata hivyo, hutofautiana katika ishara:

\[\dfrac{d}{dx} \cos x=−\sin x, \nonumber \]

lakini

\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]

Tunapoendelea uchunguzi wetu wa kazi za hyperbolic, tunapaswa kukumbuka kufanana na tofauti zao kwa kazi za kawaida za trigonometric. Njia hizi za kutofautisha kwa kazi za hyperbolic zinaongoza moja kwa moja kwenye kanuni zifuatazo muhimu.

\[ \begin{align} \int \sinh u \,du &=\cosh u+C \\[4pt] \int \text{csch}^2 u \, du &=−\coth u+C \\[4pt] \int \cosh u \,du &=\sinh u+C \\[4pt] \int \text{sech} \,u \tanh u \,du &=−\text{sech } \,u+C−\text{csch} \,u+C \\[4pt] \int \text{sech }^2u \,du &=\tanh u+C \\[4pt] \int \text{csch} \,u \coth u \,du &=−\text{csch} \,u+C \end{align} \nonumber \]

Mfano\(\PageIndex{1}\): Differentiating Hyperbolic Functions

Tathmini derivatives zifuatazo:

\(\dfrac{d}{dx}(\sinh(x^2))\)
\(\dfrac{d}{dx}(\cosh x)^2\)

Suluhisho:

Kutumia formula katika Jedwali\(\PageIndex{1}\) na utawala wa mnyororo, tunapata

\(\dfrac{d}{dx}(\sinh(x^2))=\cosh(x^2)⋅2x\)
\(\dfrac{d}{dx}(\cosh x)^2=2\cosh x\sinh x\)

Zoezi\(\PageIndex{1}\)

Tathmini derivatives zifuatazo:

\(\dfrac{d}{dx}(\tanh(x^2+3x))\)
\(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)\)

Kidokezo: Tumia fomu katika Jedwali\(\PageIndex{1}\) na utumie utawala wa mnyororo kama inavyohitajika.
Jibu: \(\dfrac{d}{dx}(\tanh(x^2+3x))=(\text{sech}^2(x^2+3x))(2x+3)\)
Jibu b: \(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)=\dfrac{d}{dx}(\sinh x)^{−2}=−2(\sinh x)^{−3}\cosh x\)

Mfano\(\PageIndex{2}\): Integrals Involving Hyperbolic Functions

Tathmini integrals zifuatazo:

\( \displaystyle \int x\cosh(x^2)dx\)
\( \displaystyle \int \tanh x\,dx\)

Suluhisho

Tunaweza kutumia\(u\) -badala katika kesi zote mbili.

a\(u=x^2\). Kisha,\(du=2x\,dx\) na

\[\begin{align*} \int x\cosh (x^2)dx &=\int \dfrac{1}{2}\cosh u\,du \\[4pt] &=\dfrac{1}{2}\sinh u+C \\[4pt] &=\dfrac{1}{2}\sinh (x^2)+C. \end{align*}\]

b Hebu\(u=\cosh x\). Kisha,\(du=\sinh x\,dx\) na

\[\begin{align*} \int \tanh x \,dx &=\int \dfrac{\sinh x}{\cosh x}\,dx \\[4pt] &=\int \dfrac{1}{u}du \\[4pt] &=\ln|u|+C \\[4pt] &= \ln|\cosh x|+C.\end{align*}\]

Kumbuka kwamba\(\cosh x>0\) kwa ajili ya wote\(x\), ili tuweze kuondoa kabisa thamani ishara na kupata

\[\int \tanh x \,dx=\ln(\cosh x)+C. \nonumber \]

Zoezi\(\PageIndex{2}\)

Tathmini integrals zifuatazo:

\(\displaystyle \int \sinh^3x \cosh x \,dx\)
\(\displaystyle \int \text{sech }^2(3x)\, dx\)

Kidokezo: Tumia formula hapo juu na uomba\(u\) -badala kama inavyohitajika.
Jibu: \(\displaystyle \int \sinh^3x \cosh x \,dx=\dfrac{\sinh^4x}{4}+C\)
Jibu b: \(\displaystyle \int \text{sech }^2(3x) \, dx=\dfrac{\tanh(3x)}{3}+C\)

Calculus ya Inverse Hyperbolic Kazi

Kuangalia grafu za kazi za hyperbolic, tunaona kwamba kwa vikwazo vinavyofaa, wote wana inverses. Vikwazo vingi muhimu vinaweza kutambuliwa kwa uchunguzi wa karibu wa grafu. Domains na safu ya kazi inverse hyperbolic ni muhtasari katika Jedwali\(\PageIndex{2}\).

Jedwali\(\PageIndex{2}\): Domains na Ranges ya Inverse Hyperbolic Kazi
Kazi	Domain	Range
\(\sinh^{−1}x\)	(,)	(,)
\(\cosh^{−1}x\)	(1,)	[0,)
\(\tanh^{−1}x\)	(-1,1)	(,)
\(\coth^{−1}x\)	(-,1) (1,)	(-,0) (0,)
\(\text{sech}^{−1}x\)	(0,1)	[0,)
\(\text{csch}^{−1}x\)	(-,0) (0,)	(-,0) (0,)

Grafu za kazi za inverse za hyperbolic zinaonyeshwa kwenye takwimu ifuatayo.

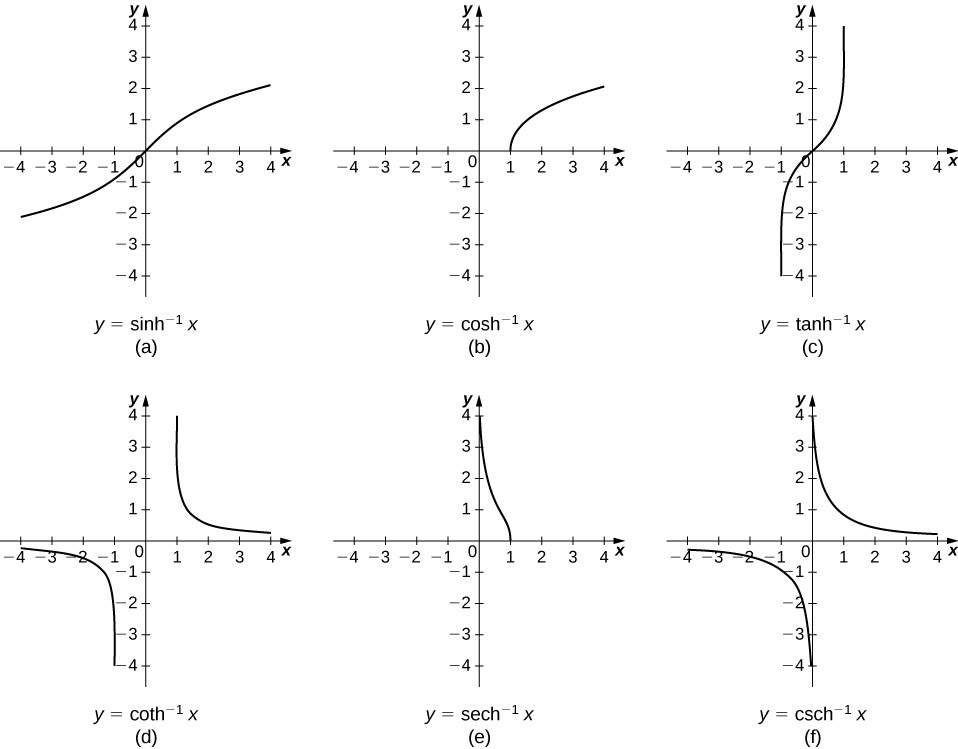
Takwimu hii ina grafu sita. Grafu ya kwanza iliyoandikwa “a” ni ya kazi y=sinh ^-1 (x). Ni kazi inayoongezeka kutoka kwa roboduara ya 3, kwa njia ya asili hadi quadrant ya kwanza. Grafu ya pili inaitwa “b” na ni ya kazi y=cosh^-1 (x). Ni katika quadrant ya kwanza, kuanzia kwenye x-axis saa 2 na kuongezeka. Grafu ya tatu iliyoandikwa “c” ni ya kazi y=tanh ^ -1 (x). Ni kazi inayoongezeka kutoka kwa quadrant ya tatu, kwa njia ya asili, hadi quadrant ya kwanza. Grafu ya nne inaitwa “d” na ni ya kazi y = kitambaa ^-1 (x). Ina vipande viwili, moja katika quadrant ya tatu na moja katika quadrant ya kwanza yenye asymptote ya wima kwenye mhimili wa y. Grafu ya tano imeandikwa “e” na ni ya kazi y=sech ^-1 (x). Ni curve kupungua katika roboduara ya kwanza na kuacha juu ya x-axis katika x=1. Grafu ya sita imeandikwa “f” na ni ya kazi y=csch^-1 (x). Ina vipande viwili, moja katika quadrant ya tatu na moja katika quadrant ya kwanza yenye asymptote ya wima kwenye mhimili wa y. — Kielelezo\(\PageIndex{3}\): Grafu ya kazi inverse hyperbolic.

Ili kupata derivatives ya kazi inverse, tunatumia tofauti thabiti. Tuna

\[\begin{align} y &=\sinh^{−1}x \\[4pt] \sinh y &=x \\[4pt] \dfrac{d}{dx} \sinh y &=\dfrac{d}{dx}x \\[4pt] \cosh y\dfrac{dy}{dx} &=1. \end{align} \nonumber \]

Kumbuka kwamba\(\cosh^2y−\sinh^2y=1,\)\(\cosh y=\sqrt{1+\sinh^2y}\) hivyo.Kisha,

\[\dfrac{dy}{dx}=\dfrac{1}{\cosh y}=\dfrac{1}{\sqrt{1+\sinh^2y}}=\dfrac{1}{\sqrt{1+x^2}}. \nonumber \]

Tunaweza hupata fomula tofauti kwa ajili ya kazi nyingine inverse hyperbolic katika mtindo sawa. Hizi formula tofauti ni muhtasari katika Jedwali\(\PageIndex{3}\).

Jedwali\(\PageIndex{3}\): Derivatives ya Kazi za Inverse Hyperbolic
\(f(x)\)	\(\dfrac{d}{dx}f(x)\)
\ (f (x)\)” style="wima align:katikati; ">\(\sinh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="wima align:katikati; ">\(\dfrac{1}{\sqrt{1+x^2}}\)
\ (f (x)\)” style="wima align:katikati; ">\(\cosh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="wima align:katikati; ">\(\dfrac{1}{\sqrt{x^2−1}}\)
\ (f (x)\)” style="wima align:katikati; ">\(\tanh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="wima align:katikati; ">\(\dfrac{1}{1−x^2}\)
\ (f (x)\)” style="wima align:katikati; ">\(\coth^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="wima align:katikati; ">\(\dfrac{1}{1−x^2}\)
\ (f (x)\)” style="wima align:katikati; ">\(\text{sech}^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="wima align:katikati; ">\(\dfrac{−1}{x\sqrt{1−x^2}}\)
\ (f (x)\)” style="wima align:katikati; ">\(\text{csch}^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)” style="wima align:katikati; ">\(\dfrac{−1}{\|x\|\sqrt{1+x^2}}\)

Kumbuka kuwa derivatives ya\(\tanh^{−1}x\) na\(\coth^{−1}x\) ni sawa. Hivyo, wakati sisi kuunganisha\(1/(1−x^2)\), tunahitaji kuchagua antiderivative sahihi kulingana na uwanja wa kazi na maadili ya\(x\). Fomu za ushirikiano zinazohusisha kazi za inverse za hyperbolic zinafupishwa kama ifuatavyo.

\[\int \dfrac{1}{\sqrt{1+u^2}}du=\sinh^{−1}u+C \nonumber \]

\[\int \dfrac{1}{u\sqrt{1−u^2}}du=−\text{sech}^{−1}|u|+C \nonumber \]

\[\int \dfrac{1}{\sqrt{u^2−1}}du=\cosh^{−1}u+C \nonumber \]

\[\int \dfrac{1}{u\sqrt{1+u^2}}du=−\text{csch}^{−1}|u|+C \nonumber \]

\[\int \dfrac{1}{1−u^2}du=\begin{cases}\tanh^{−1}u+C & \text{if }|u|<1\\ \coth^{−1}u+C & \text{if }|u|>1\end{cases} \nonumber \]

Mfano\(\PageIndex{3}\): Differentiating Inverse Hyperbolic Functions

Tathmini derivatives zifuatazo:

\(\dfrac{d}{dx}\left(\sinh^{−1}\left(\dfrac{x}{3}\right)\right)\)
\(\dfrac{d}{dx}\left(\tanh^{−1}x\right)^2\)

Suluhisho

Kutumia formula katika Jedwali\(\PageIndex{3}\) na utawala wa mnyororo, tunapata matokeo yafuatayo:

\(\dfrac{d}{dx}(\sinh^{−1}(\dfrac{x}{3}))=\dfrac{1}{3\sqrt{1+\dfrac{x^2}{9}}}=\dfrac{1}{\sqrt{9+x^2}}\)
\(\dfrac{d}{dx}(\tanh^{−1}x)^2=\dfrac{2(\tanh^{−1}x)}{1−x^2}\)

Zoezi\(\PageIndex{3}\)

Tathmini derivatives zifuatazo:

\(\dfrac{d}{dx}(\cosh^{−1}(3x))\)
\(\dfrac{d}{dx}(\coth^{−1}x)^3\)

Kidokezo: Tumia fomu katika Jedwali\(\PageIndex{3}\) na utumie utawala wa mnyororo kama inavyohitajika.
Jibu: \(\dfrac{d}{dx}(\cosh^{−1}(3x))=\dfrac{3}{\sqrt{9x^2−1}} \)
Jibu b: \(\dfrac{d}{dx}(\coth^{−1}x)^3=\dfrac{3(\coth^{−1}x)^2}{1−x^2} \)

Mfano\(\PageIndex{4}\): Integrals Involving Inverse Hyperbolic Functions

Tathmini integrals zifuatazo:

\(\displaystyle \int \dfrac{1}{\sqrt{4x^2−1}}dx\)
\(\displaystyle \int \dfrac{1}{2x\sqrt{1−9x^2}}dx\)

Suluhisho

Tunaweza kutumia \(u\)-badala katika kesi zote mbili.

Hebu\(u=2x\). Kisha,\(du=2\,dx\) na tuna

\[\begin{align*} \int \dfrac{1}{\sqrt{4x^2−1}}\,dx &=\int \dfrac{1}{2\sqrt{u^2−1}}\,du \\[4pt] &=\dfrac{1}{2}\cosh^{−1}u+C \\[4pt] &=\dfrac{1}{2}\cosh^{−1}(2x)+C. \end{align*} \nonumber \]

Basi\(u=3x.\) basi,\(du=3\,dx\) na sisi kupata

\[\begin{align*} \int \dfrac{1}{2x\sqrt{1−9x^2}}dx &=\dfrac{1}{2}\int \dfrac{1}{u\sqrt{1−u^2}}du \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|u|+C \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|3x|+C \end{align*}\]

Zoezi\(\PageIndex{4}\)

Tathmini integrals zifuatazo:

\(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx,x>2\)
\(\displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx\)

Kidokezo: Tumia formula hapo juu na uomba\(u\) -badala kama inavyohitajika.
Jibu: \(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx=\cosh^{−1}(\dfrac{x}{2})+C\)
Jibu b: \( \displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx=−\text{sech}^{−1}(e^x)+C\)

Maombi

Matumizi moja ya kimwili ya kazi za hyperbolic inahusisha nyaya za kunyongwa. Ikiwa cable ya wiani sare imesimamishwa kati ya misaada miwili bila mzigo wowote isipokuwa uzito wake mwenyewe, cable huunda safu inayoitwa catenary. Mistari ya nguvu ya juu-voltage, minyororo kunyongwa kati ya machapisho mawili, na vipande vya mtandao wa buibui kila aina ya catenaries. Takwimu inayofuata inaonyesha minyororo iliyowekwa kwenye safu ya machapisho.

Picha ya minyororo iliyowekwa kati ya machapisho ambayo yote huchukua sura ya catenary. — Kielelezo\(\PageIndex{3}\): Minyororo kati ya machapisho haya huchukua sura ya catenary. (mikopo: mabadiliko ya kazi na OkFoundryCompany, Flickr)

Kazi za hyperbolic zinaweza kutumika kutengeneza catenaries. Hasa, kazi za fomu\(y=a\cdot \cosh(x/a)\) ni catenaries. Kielelezo\(\PageIndex{4}\) inaonyesha grafu ya\(y=2\cosh(x/2)\).

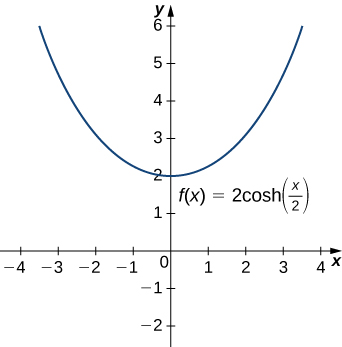
Takwimu hii ni grafu. Ni ya kazi f (x) =2cosh (x/2). Curve hupungua katika quadrant ya pili kwa y axis. Inaingiliana na mhimili wa y katika y=2. Kisha curve inakuwa kuongezeka. — Kielelezo\(\PageIndex{4}\): Kazi ya cosine ya hyperbolic huunda sura ya catenary.

Mfano\(\PageIndex{5}\): Using a Catenary to Find the Length of a Cable

Fikiria cable ya kunyongwa ina sura\(10\cosh(x/10)\) ya\(−15≤x≤15\), wapi\(x\) hupimwa kwa miguu. Kuamua urefu wa cable (kwa miguu).

Suluhisho

Kumbuka kutoka Sehemu ya 6.4 kwamba formula kwa urefu wa arc ni

\[\underbrace{\int ^b_a\sqrt{1+[f′(x)]^2}dx}_{\text{Arc Length}}. \nonumber \]

Tuna\(f(x)=10 \cosh(x/10)\), hivyo\(f′(x)=\sinh(x/10)\). Kisha urefu wa arc ni

\[\int ^b_a\sqrt{1+[f′(x)]^2}dx=\int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx. \nonumber \]

Sasa kukumbuka kwamba

\[1+\sinh^2x=\cosh^2x, \nonumber \]

hivyo tuna

\[\begin{align*} \text{Arc Length} &= \int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx \\[4pt] &=\int ^{15}_{−15}\cosh \left(\dfrac{x}{10}\right)dx \\[4pt] &= \left.10\sinh \left(\dfrac{x}{10}\right)\right|^{15}_{−15}\\[4pt] &=10\left[\sinh\left(\dfrac{3}{2}\right)−\sinh\left(−\dfrac{3}{2}\right)\right]\\[4pt] &=20\sinh \left(\dfrac{3}{2}\right) \\[4pt] &≈42.586\,\text{ft.} \end{align*}\]

Zoezi\(\PageIndex{5}\):

Fikiria cable ya kunyongwa ina sura\(15 \cosh (x/15)\) ya\(−20≤x≤20\). Kuamua urefu wa cable (kwa miguu).

Jibu: \(52.95\)ft

Dhana muhimu

Kazi ya hyperbolic hufafanuliwa kwa suala la kazi za kielelezo.
Ufafanuzi wa neno kwa muda huzalisha fomula za kutofautisha kwa kazi za hyperbolic. Njia hizi za kutofautisha hutoa, kwa upande wake, kwa formula za ushirikiano.
Kwa vikwazo vilivyofaa, kazi za hyperbolic zote zina inverses.
Tofauti thabiti hutoa formula tofauti kwa kazi inverse hyperbolic, ambayo kwa upande kutoa kupanda kwa formula ushirikiano.
Matumizi ya kawaida ya kimwili ya kazi za hyperbolic ni mahesabu yanayohusisha catenaries.

faharasa

catenary: curve katika sura ya kazi\(y=a\cdot\cosh(x/a)\) ni catenary; cable ya wiani sare imesimamishwa kati ya misaada miwili inachukua sura ya catenary