6.8: Ukuaji wa Kielelezo na Kuoza
- Page ID
- 178324
- Matumizi kielelezo ukuaji mfano katika maombi, ikiwa ni pamoja na ukuaji wa idadi ya watu na maslahi kiwanja.
- Eleza dhana ya muda wa mara mbili.
- Matumizi kielelezo kuoza mfano katika maombi, ikiwa ni pamoja na mionzi kuoza na sheria Newton ya baridi.
- Eleza dhana ya nusu ya maisha.
Moja ya maombi yaliyoenea zaidi ya kazi za kielelezo inahusisha mifano ya ukuaji na kuoza. Ukuaji wa kielelezo na kuoza huonekana katika mwenyeji wa maombi ya asili. Kutokana na ukuaji wa idadi ya watu na kuendelea imezungukwa maslahi ya kuoza mionzi na sheria Newton ya baridi, kazi kielelezo ni ubiquitous katika asili. Katika sehemu hii, sisi kuchunguza ukuaji kielelezo na kuoza katika mazingira ya baadhi ya maombi haya.
Kielelezo ukuaji Model
Mifumo mingi inaonyesha ukuaji wa kielelezo. Mifumo hii inafuata mfano wa fomu\(y=y_0e^{kt},\) ambapo\(y_0\) inawakilisha hali ya awali ya mfumo na\(k\) ni mara kwa mara chanya, inayoitwa mara kwa mara ya ukuaji. Kumbuka kwamba katika mfano wa ukuaji wa kielelezo, tuna
\[ y′=ky_0e^{kt}=ky. \label{eq1} \]
Hiyo ni, kiwango cha ukuaji ni sawa na thamani ya sasa ya kazi. Hii ni kipengele muhimu cha ukuaji wa kielelezo. Equation\ ref {eq1} inahusisha derivatives na inaitwa equation tofauti.
Mifumo inayoonyesha ongezeko la ukuaji wa kielelezo kulingana na mfano wa hisabati
\[y=y_0e^{kt} \nonumber \]
ambapo\(y_0\) inawakilisha hali ya awali ya mfumo na\(k>0\) ni mara kwa mara, inayoitwa ukuaji wa mara kwa mara.
Ukuaji wa idadi ya watu ni mfano wa kawaida wa ukuaji wa kielelezo. Fikiria idadi ya bakteria, kwa mfano. Inaonekana plausible kwamba kiwango cha ukuaji wa idadi ya watu itakuwa sawia na ukubwa wa idadi ya watu. Baada ya yote, bakteria zaidi kuna kuzaliana, idadi ya watu inakua kwa kasi. Kielelezo\(\PageIndex{1}\) na Jedwali\(\PageIndex{1}\) linawakilisha ukuaji wa idadi ya bakteria yenye idadi ya awali ya bakteria 200 na ukuaji wa mara kwa mara wa 0.02. Angalia kwamba baada ya masaa 2 tu (dakika 120), idadi ya watu ni mara 10 ukubwa wake wa awali!
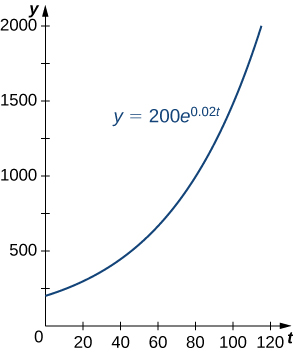
| Muda (min) | Idadi ya Watu Size (idadi ya bakteria) |
|---|---|
| 10 | 244 |
| 20 | 298 |
| 30 | 364 |
| 40 | 445 |
| 50 | 544 |
| 60 | 664 |
| 70 | 811 |
| 80 | 991 |
| 90 | 1210 |
| 100 | 1478 |
| 110 | 1805 |
| 120 | 2205 |
Kumbuka kwamba sisi ni kutumia kazi ya kuendelea kwa mfano kile asili kipekee tabia. Wakati wowote, idadi halisi ya watu duniani ina idadi nzima ya bakteria, ingawa mfano unachukua maadili yasiyo ya integer. Wakati wa kutumia mifano ya ukuaji wa kielelezo, lazima tuwe makini kutafsiri maadili ya kazi katika mazingira ya uzushi tunayofanya mfano.
Fikiria idadi ya bakteria iliyoelezwa mapema. Idadi hii inakua kulingana na kazi\(f(t)=200e^{0.02t},\) ambapo t inapimwa kwa dakika. Ni bakteria ngapi zilizopo katika idadi ya watu baada ya\(5\) masaa (\(300\)dakika)? Idadi ya watu hufikia\(100,000\) lini bakteria?
Suluhisho
Tuna\(f(t)=200e^{0.02t}.\) Basi
\[ f(300)=200e^{0.02(300)}≈80,686. \nonumber \]
Kuna\(80,686\) bakteria katika idadi ya watu baada ya\(5\) masaa.
Ili kupata wakati idadi ya watu kufikia\(100,000\) bakteria, sisi kutatua equation
\[ \begin{align*} 100,000 &= 200e^{0.02t} \\[4pt] 500 &=e^{0.02t} \\[4pt] \ln 500 &=0.02 t \\[4pt] t &=\frac{\ln 500}{0.02}≈310.73. \end{align*} \nonumber \]
Idadi ya watu hufikia\(100,000\) bakteria baada ya\(310.73\) dakika.
Fikiria idadi ya bakteria ambayo inakua kulingana na kazi\(f(t)=500e^{0.05t}\), ambapo\(t\) hupimwa kwa dakika. Ni bakteria ngapi zilizopo katika idadi ya watu baada ya masaa 4? Idadi ya watu hufikia\(100\) lini bakteria milioni?
- Jibu
-
Tumia mchakato kutoka kwa mfano uliopita.
- Jibu
-
Kuna\(81,377,396\) bakteria katika idadi ya watu baada ya\(4\) masaa. Idadi ya watu hufikia bakteria\(100\) milioni baada ya\(244.12\) dakika.
Hebu sasa tutazingatia maombi ya kifedha: maslahi ya kiwanja. Maslahi ambayo haijasumbuliwa inaitwa riba rahisi. Maslahi rahisi hulipwa mara moja, mwishoni mwa kipindi cha muda maalum (kawaida\(1\) mwaka). Kwa hiyo, ikiwa tunaweka\($1000\) akaunti ya akiba kupata riba\(2%\) rahisi kwa mwaka, basi mwishoni mwa mwaka tuna
\[ 1000(1+0.02)=$1020. \nonumber \]
Maslahi ya kiwanja hulipwa mara nyingi kwa mwaka, kulingana na kipindi cha kuchanganya. Kwa hiyo, ikiwa benki inachanganya riba kila\(6\) miezi, inatoa nusu ya maslahi ya mwaka kwa akaunti baada ya\(6\) miezi. Katika nusu ya pili ya mwaka, akaunti hupata riba sio tu kwa awali\($1000\), lakini pia kwa riba iliyopatikana wakati wa nusu ya kwanza ya mwaka. Kihisabati akizungumza, mwishoni mwa mwaka, tuna
\[ 1000 \left(1+\dfrac{0.02}{2}\right)^2=$1020.10. \nonumber \]
Vile vile, kama maslahi ni imezungukwa kila\(4\) miezi, tuna
\[ 1000 \left(1+\dfrac{0.02}{3}\right)^3=$1020.13, \nonumber \]
na kama maslahi ni imezungukwa kila siku (\(365\)mara kwa mwaka), tuna\($1020.20\). Kama sisi kupanua dhana hii, ili riba ni imezungukwa kuendelea, baada ya\(t\) miaka tuna
\[ 1000\lim_{n→∞} \left(1+\dfrac{0.02}{n}\right)^{nt}. \nonumber \]
Sasa hebu kuendesha maneno haya ili tuwe na kazi ya ukuaji wa kielelezo. Kumbuka kwamba idadi\(e\) inaweza kuelezwa kama kikomo:
\[ e=\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m. \nonumber \]
Kulingana na hili, tunataka kujieleza ndani ya mabano kuwa na fomu\((1+1/m)\). Hebu\(n=0.02m\). Kumbuka kuwa\(n→∞, m→∞\) pia. Kisha sisi kupata
\[ 1000\lim_{n→∞}\left(1+\dfrac{0.02}{n}\right)^{nt}=1000\lim_{m→∞}\left(1+\dfrac{0.02}{0.02m}\right)^{0.02mt}=1000\left[\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m\right]^{0.02t}. \nonumber \]
Tunatambua kikomo ndani ya mabano kama namba\(e\). Hivyo, usawa katika akaunti yetu ya benki baada ya\(t\) miaka hutolewa na\(1000 e^{0.02t}\). Kuzalisha dhana hii, tunaona kwamba kama akaunti ya benki na usawa wa awali wa\($P\) chuma riba kwa kiwango cha\(r%\), imezungukwa kuendelea, basi uwiano wa akaunti baada ya\(t\) miaka ni
\[ \text{Balance}\;=Pe^{rt}. \nonumber \]
Mwanafunzi mwenye umri wa miaka 25 anapewa fursa ya kuwekeza pesa katika akaunti ya kustaafu ambayo hulipa riba ya\(5%\) kila mwaka imezungukwa kuendelea. Je, mwanafunzi anahitaji kuwekeza kiasi gani leo kuwa na\($1\) milioni wakati anastaafu akiwa na umri\(65\)? Nini kama angeweza kupata maslahi ya\(6%\) kila mwaka imezungukwa kuendelea badala?
Suluhisho
Tuna
\[ 1,000,000=Pe^{0.05(40)} \nonumber \]
\[ P=135,335.28. \nonumber \]
Lazima kuwekeza\($135,335.28\) kwa\(5%\) riba.
Kama, badala yake, yeye ni uwezo wa kupata\(6%,\) basi equation inakuwa
\[ 1,000,000=Pe^{0.06(40)} \nonumber \]
\[ P=90,717.95. \nonumber \]
Katika kesi hiyo, anahitaji kuwekeza tu\($90,717.95.\) Hii ni takribani theluthi mbili kiasi anachohitaji kuwekeza\(5%\). Ukweli kwamba maslahi yanajumuishwa daima huongeza sana athari za\(1%\) ongezeko la kiwango cha riba.
Tuseme badala ya kuwekeza wakati\(25\sqrt{b^2−4ac}\), mwanafunzi anasubiri hadi umri\(35\). Ni kiasi gani angeweza kuwekeza katika\(5%\)? Katika\(6%\)?
- Kidokezo
-
Tumia mchakato kutoka kwa mfano uliopita.
- Jibu
-
Kwa\(5%\) riba, lazima kuwekeza\($223,130.16\). Kwa\(6%\) riba, yeye lazima kuwekeza\($165,298.89.\)
Kama wingi kukua exponentially, muda inachukua kwa wingi mara mbili bado mara kwa mara. Kwa maneno mengine, inachukua kiasi sawa cha muda kwa idadi ya bakteria kukua kutoka\(100\) kwa\(200\) bakteria kama inavyofanya kukua kutoka\(10,000\) kwa\(20,000\) bakteria. Wakati huu inaitwa wakati wa mara mbili. Ili kuhesabu muda wa mara mbili, tunataka kujua wakati wingi unafikia ukubwa wake wa awali mara mbili. Hivyo tuna
\[ \begin{align*} 2y_0 &=y_0e^{kt} \\[4pt] 2 &=e^{kt} \\[4pt] \ln 2 &=kt \\[4pt] t &=\dfrac{\ln 2}{k}. \end{align*} \nonumber \]
Kama wingi kukua exponentially, muda mara mbili ni kiasi cha muda inachukua kiasi mara mbili. Ni iliyotolewa na
\[\text{Doubling time}=\dfrac{\ln 2}{k}. \nonumber \]
Fikiria idadi ya samaki inakua kwa kiasi kikubwa. Bwawa linajaa awali na\(500\) samaki. Baada ya\(6\) miezi, kuna\(1000\) samaki katika bwawa. Mmiliki atawawezesha marafiki na majirani zake samaki kwenye bwawa lake baada ya idadi ya samaki kufikia\(10,000\). Marafiki wa mmiliki wataruhusiwa samaki lini?
Suluhisho
Tunajua inachukua idadi ya\(6\) miezi ya samaki mara mbili kwa ukubwa. Kwa hiyo, ikiwa\(t\) inawakilisha muda kwa miezi, kwa formula ya mara mbili, tuna\(6=(\ln 2)/k\). Kisha,\(k=(\ln 2)/6\). Hivyo, idadi ya watu hutolewa na\(y=500e^{((\ln 2)/6)t}\). Ili kujua wakati idadi ya watu inakaribia\(10,000\) samaki, tunapaswa kutatua equation ifuatayo:
\[ \begin{align*} 10,000 &=500e^{(\ln 2/6)t} \\[4pt] 20 &=e^{(\ln 2/6)t} \\[4pt] \ln 20 &=\left(\frac{\ln 2}{6}\right)t \\[4pt] t &=\frac{6(\ln 20)}{\ln 2} \\[4pt] &≈25.93. \end{align*} \nonumber \]
Marafiki wa mmiliki wanapaswa kusubiri\(25.93\) miezi (kidogo zaidi ya\(2\) miaka) kwa samaki katika bwawa.
Tuseme inachukua\(9\) miezi kwa idadi ya samaki katika Mfano\(\PageIndex{3}\) kufikia\(1000\) samaki. Chini ya hali hizi, marafiki wa mmiliki wanapaswa kusubiri kwa muda gani?
- Kidokezo
-
Tumia mchakato kutoka kwa mfano uliopita.
- Jibu
-
\(38.90\)miezi
Kielelezo kuoza Model
Kazi za kielelezo zinaweza pia kutumiwa kutengeneza watu ambao hupungua (kutokana na ugonjwa, kwa mfano), au misombo ya kemikali ambayo huvunja baada ya muda. Tunasema kwamba mifumo hiyo inaonyesha kuoza kwa ufafanuzi, badala ya ukuaji wa kielelezo. Mfano huo ni karibu sawa, isipokuwa kuna ishara hasi katika kielelezo. Hivyo, kwa baadhi ya mara kwa mara chanya\(k\), tuna
\[ y=y_0e^{−kt}. \nonumber \]
Kama ilivyo kwa ukuaji wa kielelezo, kuna equation tofauti inayohusishwa na kuoza kwa kielelezo. Tuna
\[ y′=−ky_0e^{−kt}=−ky. \nonumber \]
Mifumo inayoonyesha kuoza kwa maonyesho hufanya kulingana na mfano
\[y=y_0e^{−kt}, \nonumber \]
ambapo\(y_0\) inawakilisha hali ya awali ya mfumo na\(k>0\) ni mara kwa mara, inayoitwa mara kwa mara kuoza.
Kielelezo\(\PageIndex{2}\) kinaonyesha grafu ya kazi ya kuoza ya mwakilishi.
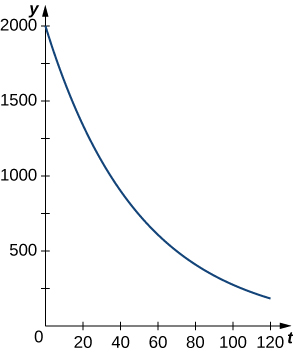
Hebu tuangalie matumizi ya kimwili ya kuoza kwa maonyesho. Sheria ya Newton ya baridi inasema kuwa kitu kinachopoza kwa kiwango sawia na tofauti kati ya halijoto ya kitu na halijoto ya mazingira. Kwa maneno mengine, ikiwa\(T\) inawakilisha joto la kitu na\(T_a\) inawakilisha joto la kawaida katika chumba, basi
\[T′=−k(T−T_a). \nonumber \]
Kumbuka kuwa hii sio mfano sahihi kabisa wa kuoza kwa maonyesho. Tunataka derivative kuwa sawia na kazi, na maneno haya ina\(T_a\) muda wa ziada. Kwa bahati nzuri, tunaweza kufanya mabadiliko ya vigezo kwamba resolves suala hili. Hebu\(y(t)=T(t)−T_a\). Kisha\(y′(t)=T′(t)−0=T′(t)\), na equation yetu inakuwa
\[ y′=−ky. \nonumber \]
Kutokana na kazi yetu ya awali, tunajua uhusiano huu kati\(y\) na derivative yake inaongoza kwa kuoza kielelezo. Hivyo,
\[ y=y_0e^{−kt}, \nonumber \]
na tunaona kwamba
\[ T−T_a=(T_0−T_a)e^{−kt} \nonumber \]
\[ T=(T_0−T_a)e^{−kt}+T_a \nonumber \]
ambapo\(T_0\) inawakilisha joto la awali. Hebu tufanye fomu hii katika mfano unaofuata.
Kulingana na baristas uzoefu, joto mojawapo ya kutumikia kahawa ni kati\(155°F\) na\(175°F\). Tuseme kahawa hutiwa kwenye joto la\(200°F\), na baada ya\(2\) dakika katika\(70°F\) chumba kilichopozwa\(180°F\). Ni wakati gani kahawa ya kwanza ya baridi ya kutosha kutumikia? Wakati kahawa ni baridi sana kutumikia? Majibu ya pande zote kwa dakika ya karibu ya nusu.
Suluhisho
Tuna
\[ \begin{align*} T &=(T_0−T_a)e^{−kt}+T_a \\[4pt] 180 &=(200−70)e^{−k(2)}+70 \\[4pt] 110 &=130e^{−2k} \\[4pt] \dfrac{11}{13} &=e^{−2k} \\[4pt] \ln \dfrac{11}{13} &=−2k \\[4pt] \ln 11−\ln 13 &=−2k \\[4pt] k &=\dfrac{\ln 13−\ln 11}{2} \end{align*}\]
Kisha, mfano ni
\[T=130e^{(\ln 11−\ln 13/2)t}+70. \nonumber \]
Kahawa hufikia\(175°F\) wakati
\[ \begin{align*} 175 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt]105 &=130e^{(\ln 11−\ln 13/2)t} \\[4pt] \dfrac{21}{26} &=e^{(\ln 11−\ln 13/2)t} \\[4pt] \ln \dfrac{21}{26} &=\dfrac{\ln 11−\ln 13}{2}t \\[4pt] \ln 21−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 21−\ln 26)}{\ln 11−\ln 13}\\[4pt] &≈2.56. \end{align*}\]
Kahawa inaweza kutumika kwa\(2.5\) muda wa dakika baada ya kumwagika. Kahawa hufikia\(155°F\)
\[ \begin{align*} 155 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt] 85 &=130e^{(\ln 11−\ln 13)t} \\[4pt] \dfrac{17}{26} &=e^{(\ln 11−\ln 13)t} \\[4pt] \ln 17−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 17−\ln 26)}{\ln 11−\ln 13} \\[4pt] &≈5.09.\end{align*}\]
Kahawa ni baridi sana kutumiwa baada ya\(5\) dakika baada ya kumwagika.
Tuseme chumba ni joto\((75°F)\) na, baada ya\(2\) dakika, kahawa ina kilichopozwa tu kwa\(185°F.\) Wakati kahawa kwanza baridi ya kutosha kutumika? Ni lini kahawa kuwa baridi sana kutumikia? Majibu ya pande zote kwa dakika ya karibu ya nusu.
- Kidokezo
-
Tumia mchakato kutoka kwa mfano uliopita.
- Jibu
-
Kahawa ni ya kwanza ya baridi ya kutosha kutumikia\(3.5\) dakika baada ya kumwagika. Kahawa ni baridi sana kutumikia\(7\) dakika baada ya kumwagika.
Kama vile mifumo inayoonyesha ukuaji wa kielelezo ina muda wa mara mbili mara mbili, mifumo inayoonyesha kuoza kwa kielelezo ina nusu ya maisha ya mara kwa mara. Ili kuhesabu nusu ya maisha, tunataka kujua wakati wingi unafikia nusu ya ukubwa wake wa awali. Kwa hiyo, tuna
\(\dfrac{y_0}{2}=y_0e^{−kt}\)
\(\dfrac{1}{2}=e^{−kt}\)
\(−\ln 2=−kt\)
\(t=\dfrac{\ln 2}{k}\).
Kumbuka: Hii ni maneno sawa tuliyokuja na kwa muda wa mara mbili.
Kama wingi kuoza exponentially, nusu ya maisha ni kiasi cha muda inachukua kiasi kupunguzwa kwa nusu. Ni iliyotolewa na
\[\text{Half-life}=\dfrac{\ln 2}{k}. \nonumber \]
Moja ya maombi ya kawaida ya mfano wa kuoza kwa maonyesho ni dating ya kaboni. Uharibifu wa kaboni-14 (hutoa chembe ya mionzi) kwa kiwango cha kawaida na thabiti cha ufafanuzi. Kwa hiyo, ikiwa tunajua kiasi gani kaboni-14 kilichokuwa awali katika kitu na kiasi gani cha kaboni-14 kinabakia, tunaweza kuamua umri wa kitu. Nusu ya maisha ya kaboni-14 ni takriban miaka 5730—maana, baada ya miaka mingi, nusu nyenzo zimebadilishwa kutoka kaboni-14 awali hadi nitrojeni mpya isiyo na mionzi 14. Ikiwa tuna 100 g kaboni-14 leo, ni kiasi gani kinachoachwa katika miaka 50? Ikiwa artifact ambayo awali ilikuwa na 100 g ya kaboni-14 sasa ina 10 g ya kaboni-14, ni umri gani? Pande jibu kwa miaka mia moja karibu.
Suluhisho
Tuna
\[ 5730=\dfrac{\ln 2}{k} \nonumber \]
\[ k=\dfrac{\ln 2}{5730}.\nonumber \]
Hivyo, mfano anasema
\[ y=100e^{−(\ln 2/5730)t}.\nonumber \]
Katika\(50\) miaka, tuna
\[y=100e^{−(\ln 2/5730)(50)}≈99.40\nonumber \]
Kwa hiyo, katika\(50\) miaka,\(99.40\) g ya kaboni-14 bado.
Kuamua umri wa artifact, ni lazima kutatua
\[ \begin{align*} 10 &=100e^{−(\ln 2/5730)t} \\[4pt] \dfrac{1}{10} &= e^{−(\ln 2/5730)t} \\ t &≈19035. \end{align*}\]
Artifact ni kuhusu umri wa\(19,000\) miaka.
Ikiwa tuna 100 g ya kaboni-14 , ni kiasi gani cha kushoto baada ya miaka 500? Kama artifact kwamba awali zilizomo 100 g ya kaboni-14 sasa ina 20 g ya kaboni-14, ni umri gani? Pande jibu kwa miaka mia moja karibu.
- Kidokezo
-
Tumia mchakato kutoka kwa mfano uliopita.
- Jibu
-
Jumla ya 94.13 g ya kaboni-14 inabaki baada ya miaka 500. Artifact ni takriban miaka 13,300.
Dhana muhimu
- Ukuaji wa kielelezo na kuoza kwa ufafanuzi ni maombi mawili ya kawaida ya kazi za kielelezo.
- Mifumo inayoonyesha ukuaji wa kielelezo hufuata mfano wa fomu\(y=y_0e^{kt}\).
- Katika ukuaji wa kielelezo, kiwango cha ukuaji ni sawa na wingi wa sasa. Kwa maneno mengine,\(y′=ky\).
- Mifumo inayoonyesha ukuaji wa kielelezo ina muda wa mara kwa mara mara mbili, unaotolewa na\((\ln 2)/k\).
- Mifumo inayoonyesha kuoza kwa ufafanuzi hufuata mfano wa fomu\(y=y_0e^{−kt}.\)
- Mifumo inayoonyesha kuoza kwa maonyesho ina nusu ya maisha ya mara kwa mara, ambayo hutolewa na\((\ln 2)/k.\)
faharasa
- mara mbili
- kama wingi kukua exponentially, muda mara mbili ni kiasi cha muda inachukua kiasi mara mbili, na ni kutolewa na\((\ln 2)/k\)
- kuoza kielelezo
- mifumo ya kuonyesha kuoza kielelezo kufuata mfano wa fomu\(y=y_0e^{−kt}\)
- ukuaji wa kielelezo
- mifumo ya kuonyesha ukuaji kielelezo kufuata mfano wa fomu\(y=y_0e^{kt}\)
- nusu ya maisha
- ikiwa kiasi kinaharibika kwa kiasi kikubwa, nusu ya maisha ni kiasi cha muda inachukua kiasi cha kupunguzwa kwa nusu. Ni iliyotolewa na\((\ln 2)/k\)


