6.1: Maeneo kati ya Curves

Last updated
Save as PDF

Page ID: 178431

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Kuamua eneo la kanda kati ya curves mbili kwa kuunganisha kwa heshima na kutofautiana kwa kujitegemea.
Pata eneo la mkoa wa kiwanja.
Kuamua eneo la kanda kati ya curves mbili kwa kuunganisha kwa heshima na kutofautiana tegemezi.

Katika Utangulizi wa Ushirikiano, tulianzisha dhana ya umuhimu wa uhakika ili kuhesabu eneo chini ya pembe kwenye kipindi kilichopewa. Katika sehemu hii, tunapanua wazo hilo kuhesabu eneo la mikoa ngumu zaidi. Tunaanza kwa kutafuta eneo kati ya curves mbili ambazo ni kazi za$\displaystyle x$, kuanzia na kesi rahisi ambayo thamani moja ya kazi daima ni kubwa kuliko nyingine. Sisi kisha kuangalia kesi wakati grafu ya kazi msalaba. Mwisho, tunazingatia jinsi ya kuhesabu eneo kati ya curves mbili ambazo ni kazi za$\displaystyle y$.

Eneo la Mkoa kati ya Curves mbili

Hebu$\displaystyle f(x)$ na$\displaystyle g(x)$ uwe na kazi zinazoendelea juu ya muda$\displaystyle [a,b]$ kama huo$\displaystyle [a,b]$.$\displaystyle f(x)≥g(x)$ Tunataka kupata eneo kati ya grafu ya kazi, kama inavyoonekana kwenye Kielelezo$\PageIndex{1}$.

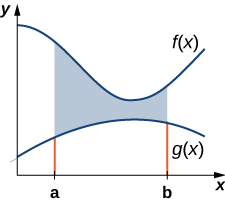
Takwimu hii ni grafu katika quadrant ya kwanza. Kuna curves mbili kwenye grafu. Curve ya juu imeandikwa “f (x)” na safu ya chini inaitwa “g (x)”. Kuna mipaka miwili juu ya x-axis kinachoitwa na b Kuna kivuli eneo kati ya curves mbili imepakana na mistari katika x=a na x = b. — Kielelezo$\PageIndex{1}$: Eneo kati ya grafu ya kazi mbili$\displaystyle g(x)$,$\displaystyle f(x)$ na, kwa muda$\displaystyle [a,b]$

Kama tulivyofanya hapo awali, tunakwenda kugawanya muda kwenye mhimili wa x na takriban eneo kati ya grafu za kazi na rectangles. Kwa hiyo, kwa$\displaystyle i=0,1,2,…,n$, basi$\displaystyle P={x_i}$ iwe sehemu ya kawaida ya$\displaystyle [a,b]$. Kisha, kwa$\displaystyle i=1,2,…,n,$ kuchagua uhakika$\displaystyle x^∗_i∈[x_{i−1},x_i]$, na kila kipindi$\displaystyle [x_{i−1},x_i]$ kujenga mstatili kwamba inaenea wima kutoka$\displaystyle g(x^∗_i)$ kwa$\displaystyle f(x^∗_i)$. Kielelezo$\PageIndex{2a}$ kinaonyesha rectangles wakati$\displaystyle x^∗_i$ umechaguliwa kuwa mwisho wa kushoto wa muda na$\displaystyle n=10$. Kielelezo$\PageIndex{2b}$ kinaonyesha mstatili wa mwakilishi kwa undani.

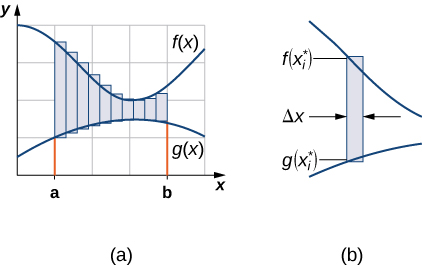
Takwimu hii ina grafu tatu. Grafu ya kwanza ina curves mbili, moja juu ya nyingine. Kati ya curves ni mstatili. Juu ya mstatili iko kwenye safu ya juu iliyoandikwa “f (x*)” na chini ya mstatili iko kwenye pembe ya chini na iliyoandikwa “g (x*)”. Grafu ya pili, iliyoitwa “(a)”, ina curves mbili kwenye grafu. Curve ya juu imeandikwa “f (x)” na safu ya chini inaitwa “g (x)”. Kuna kivuli eneo kati ya curves mbili imepakana na mistari katika x = na x = b. grafu ya tatu, kinachoitwa “(b)” ina curves mbili moja juu ya nyingine. Curve ya kwanza inaitwa “f (x*)” na safu ya chini inaitwa “g (x*)”. Kuna mstatili wa kivuli kati ya hizo mbili. Upana wa mstatili umeandikwa kama “delta x”. — Kielelezo$\PageIndex{2}$: (a) Tunaweza takriban eneo kati ya grafu za kazi mbili,$\displaystyle f(x)$ na$\displaystyle g(x)$, na mstatili. (b) Eneo la mstatili wa kawaida huenda kutoka kwenye pembe moja hadi nyingine.

Urefu wa kila mstatili wa mtu binafsi ni$\displaystyle f(x^∗_i)−g(x^∗_i)$ na upana wa kila mstatili ni$\displaystyle Δx$. Kuongeza maeneo ya rectangles zote, tunaona kwamba eneo kati ya curves ni takriban na

\[\displaystyle A≈\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx. \nonumber \]

Hii ni jumla Riemann, hivyo sisi kuchukua kikomo kama$\displaystyle n→∞$ na sisi kupata

\[\displaystyle A=\lim_{n→∞}\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Matokeo haya ni muhtasari katika theorem zifuatazo.

Kupata Eneo kati ya Curves mbili

Hebu$\displaystyle f(x)$ na$\displaystyle g(x)$ kuwa kazi ya kuendelea kama kwamba$\displaystyle f(x)≥g(x)$ zaidi ya muda [$\displaystyle a,b]$. Hebu R inaashiria eneo lililofungwa hapo juu na grafu ya$\displaystyle f(x)$, chini na grafu ya$\displaystyle g(x)$, na upande wa kushoto na kulia kwa mistari$\displaystyle x=a$ na$\displaystyle x=b$, kwa mtiririko huo. Kisha, eneo la$\textbf{R}$ hutolewa na

\[A=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Tunatumia theorem hii katika mfano wafuatayo.

Mfano$\PageIndex{1}$: Finding the Area of a Region between Two Curves I

Ikiwa$\textbf{R}$ ni kanda iliyofungwa hapo juu na grafu ya kazi$\displaystyle f(x)=x+4$ na chini na grafu ya kazi$\displaystyle g(x)=3−\dfrac{x}{2}$ juu ya muda$\displaystyle [1,4]$, tafuta eneo la kanda$\textbf{R}$.

Suluhisho

Mkoa unaonyeshwa katika takwimu zifuatazo.

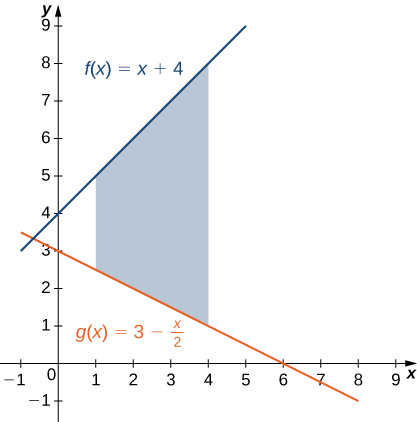
Takwimu hii ina grafu mbili za mstari katika quadrant ya kwanza. Wao ni kazi f (x) = x+4 na g (x) = 3-x/2. Kati ya mistari hii ni eneo la kivuli, lililofungwa hapo juu na f (x) na chini na g (x). Eneo la kivuli ni kati ya x=1 na x=4. — Kielelezo$\PageIndex{3}$: kanda kati ya curves mbili ni umeonyesha ambapo Curve moja daima ni kubwa kuliko nyingine.

Tuna

\[ \begin{align*} A =\int ^b_a[f(x)−g(x)]\,dx \\[4pt] =\int ^4_1[(x+4)−(3−\dfrac{x}{2})]\,dx=\int ^4_1\left[\dfrac{3x}{2}+1\right]\,dx \\[4pt] =[\dfrac{3x^2}{4}+x]\bigg|^4_1=(16−\dfrac{7}{4})=\dfrac{57}{4}. \end{align*}\]

Eneo la mkoa ni$\displaystyle \dfrac{57}{4}units^2$.

Zoezi$\PageIndex{1}$

Ikiwa$\textbf{R}$ ni kanda iliyofungwa na grafu za kazi$\displaystyle f(x)=\dfrac{x}{2}+5$ na$\displaystyle g(x)=x+\dfrac{1}{2}$ zaidi ya muda$\displaystyle [1,5]$, tafuta eneo la kanda$\textbf{R}$.

Kidokezo: Grafu kazi ya kuamua ni graph kazi ya aina ya juu amefungwa na ambayo fomu ya chini amefungwa, kisha kufuata mchakato kutumika katika Mfano.

Jibu: $\displaystyle 12$vitengo ²

Katika Mfano$\PageIndex{1}$, tulifafanua muda wa riba kama sehemu ya taarifa ya tatizo. Mara nyingi, ingawa, tunataka kufafanua muda wetu wa maslahi kulingana na ambapo grafu za kazi mbili zinaingiliana. Hii inaonyeshwa katika mfano wafuatayo.

Mfano$\PageIndex{2}$: Finding the Area of a Region between Two Curves II

Ikiwa$\textbf{R}$ ni eneo lililofungwa hapo juu na grafu ya kazi$\displaystyle f(x)=9−(x/2)^2$ na chini na grafu ya kazi$\displaystyle g(x)=6−x$, tafuta eneo la kanda$\textbf{R}$.

Suluhisho

Mkoa unaonyeshwa katika takwimu zifuatazo.

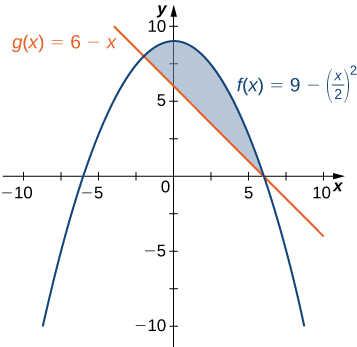
Takwimu hii ina grafu mbili katika quadrant ya kwanza. Wao ni kazi f (x) = 9- (x/2) ^2 na g (x) = 6-x. Kati ya grafu hizi, kichwa chini parabola na mstari, ni eneo la kivuli, lililofungwa hapo juu na f (x) na chini na g (x). — Kielelezo$\PageIndex{4}$: Grafu hii inaonyesha kanda chini ya grafu ya$\displaystyle f(x)$ na juu ya grafu ya$\displaystyle g(x).$

Sisi kwanza tunahitaji kuhesabu ambapo grafu za kazi zinaingiliana. Kuweka$\displaystyle f(x)=g(x),$ tunapata

\[ \begin{align*} \displaystyle f(x) =g(x) \\[4pt] 9−(\dfrac{x}{2})^2 =6−x\\[4pt] 9−\dfrac{x^2}{4} =6−x\\[4pt] 36−x^2 =24−4x\\[4pt] x^2−4x−12 =0\\[4pt] (x−6)(x+2) =0. \end{align*}\]

Grafu za kazi zinaingiliana wakati$\displaystyle x=6$ au$\displaystyle x=−2,$ hivyo tunataka kuunganisha kutoka$\displaystyle −2$ kwa$\displaystyle 6$. Tangu$\displaystyle f(x)≥g(x)$ kwa$\displaystyle −2≤x≤6,$ sisi kupata

\[\begin{align*} \displaystyle A =\int ^b_a[f(x)−g(x)]\,dx \\ =\int ^6_{−2} \left[9−(\dfrac{x}{2})^2−(6−x)\right]\,dx \\ =\int ^6_{−2}\left[3−\dfrac{x^2}{4}+x\right]\,dx \\ = \left. \left[3x−\dfrac{x^3}{12}+\dfrac{x^2}{2}\right] \right|^6_{−2}=\dfrac{64}{3}. \end{align*}\]

Eneo la mkoa ni$\displaystyle 64/3$ vitengo ².

Zoezi$\PageIndex{2}$

Ikiwa$\textbf{R}$ ni eneo lililofungwa hapo juu na grafu ya kazi$\displaystyle f(x)=x$ na chini na grafu ya kazi$\displaystyle g(x)=x^4$, tafuta eneo la kanda$\textbf{R}$.

Kidokezo: Tumia mchakato kutoka Mfano$\PageIndex{2}$.

Jibu: $\displaystyle \dfrac{3}{10}$kitengo cha ²

Maeneo ya Mikoa ya Muundo

Hadi sasa, tuna required$\displaystyle f(x)≥g(x)$ juu ya muda mzima wa riba, lakini nini kama tunataka kuangalia mikoa imepakana na grafu ya kazi kwamba kuvuka kila mmoja? Katika kesi hiyo, sisi kurekebisha mchakato sisi tu maendeleo kwa kutumia thamani kamili kazi.

Kutafuta Eneo la Mkoa kati ya Curves Hiyo Msalaba

Hebu$\displaystyle f(x)$ na$\displaystyle g(x)$ uwe na kazi zinazoendelea juu ya muda$\displaystyle [a,b]$. Hebu$\textbf{R}$ kuashiria kanda kati ya grafu ya$\displaystyle f(x)$ na$\displaystyle g(x)$, na imefungwa upande wa kushoto na kulia na mistari$\displaystyle x=a$ na$\displaystyle x=b$, kwa mtiririko huo. Kisha, eneo la$\textbf{R}$ hutolewa na

\[A=\int ^b_a|f(x)−g(x)|dx. \nonumber \]

Katika mazoezi, kutumia theorem hii inahitaji sisi kuvunja muda$\displaystyle [a,b]$ na kutathmini integrals kadhaa, kulingana na ambayo ya maadili ya kazi ni kubwa zaidi juu ya sehemu fulani ya muda. Tunasoma mchakato huu katika mfano wafuatayo.

Mfano$\PageIndex{3}$: Finding the Area of a Region Bounded by Functions That Cross

Ikiwa$\textbf{R}$ ni kanda kati ya grafu za kazi$\displaystyle f(x)=\sin x $ na$\displaystyle g(x)=\cos x$ zaidi ya muda$\displaystyle [0,π]$, tafuta eneo la kanda$\textbf{R}$.

Suluhisho

Mkoa unaonyeshwa katika takwimu zifuatazo.

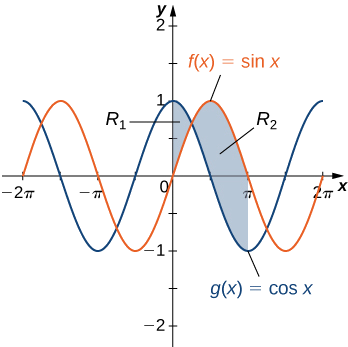
Takwimu hii ina grafu mbili. Wao ni kazi f (x) = sinx na g (x) = cosx. Wote ni kazi za mara kwa mara zinazofanana na mawimbi. Kuna maeneo mawili ya kivuli kati ya grafu. Eneo la kwanza la kivuli linaitwa “R1” na ina g (x) juu ya f (x). Mkoa huu huanza kwenye mhimili wa y na huacha ambapo curves huingiliana. Eneo la pili linaitwa “R2” na huanza katika makutano na f (x) juu ya g (x). Eneo la kivuli linaacha saa x=pi. — Kielelezo$\PageIndex{5}$: Kanda kati ya curves mbili inaweza kuvunjwa katika mikoa miwili ndogo.

Grafu za kazi zinaingiliana$\displaystyle x=π/4$. Kwa$\displaystyle x∈[0,π/4], \cos x≥\sin x ,$ hivyo

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x .$

Kwa upande mwingine, kwa$\displaystyle x∈[π/4,π], \sin x ≥\cos x,$ hivyo

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\sin x −\cos x.$

Kisha

\[ \begin{align*} A =\int ^b_a|f(x)−g(x)|dx \\[4pt] =\int ^π_0|\sin x −\cos x|dx=\int ^{π/4}_0(\cos x−\sin x )dx+\int ^{π}_{π/4}(\sin x −\cos x)dx \\[4pt] =[\sin x +\cos x]|^{π/4}_0+[−\cos x−\sin x ]|^π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \end{align*}\]

Eneo la mkoa ni$\displaystyle 2\sqrt{2}$ vitengo ^₂.

Zoezi$\PageIndex{3}$

Ikiwa$\textbf{R}$ ni kanda kati ya grafu za kazi$\displaystyle f(x)=\sin x $ na$\displaystyle g(x)=\cos x$ zaidi ya muda$\displaystyle [π/2,2π]$, tafuta eneo la kanda$\textbf{R}$.

Kidokezo: curves mbili intersect katika$\displaystyle x=(5π)/4.$

Jibu: $\displaystyle 2+2\sqrt{2}$vitengo ²

Mfano$\PageIndex{4}$: Finding the Area of a Complex Region

Fikiria kanda iliyoonyeshwa kwenye Kielelezo$\PageIndex{6}$. Kupata eneo la$\textbf{R}$.

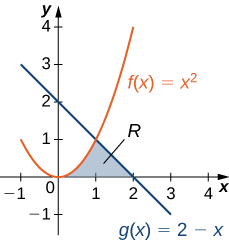
Takwimu hii ina grafu mbili katika quadrant ya kwanza. Wao ni kazi f (x) = x ^ 2 na g (x) = 2-x. Kati ya grafu hizi ni eneo la kivuli, lililofungwa upande wa kushoto na f (x) na kulia kwa g (x). Yote ambayo ni juu ya x-axis. Eneo limeandikwa R. eneo la kivuli ni kati ya x=0 na x=2. — Kielelezo$\PageIndex{6}$: Integrals mbili zinahitajika kuhesabu eneo la mkoa huu.

Suluhisho

Kama ilivyo kwa Mfano$\PageIndex{3}$, tunahitaji kugawanya muda katika vipande viwili. Grafu za kazi zinaingiliana$\displaystyle x=1$ (kuweka$\displaystyle f(x)=g(x)$ na kutatua kwa x), kwa hiyo tunatathmini integrals mbili tofauti: moja juu ya muda$\displaystyle [0,1]$ na moja juu ya muda$\displaystyle [1,2]$.

Zaidi ya muda$\displaystyle [0,1]$, kanda imefungwa hapo juu$\displaystyle f(x)=x^2$ na chini na x-axis, kwa hiyo tuna

$\displaystyle A_1=\int ^1_0x^2dx=\dfrac{x^3}{3}∣^1_0=\dfrac{1}{3}.$

Zaidi$\displaystyle [1,2],$ ya muda kanda imefungwa hapo juu$\displaystyle g(x)=2−x$ na chini na x-axis, kwa hiyo tuna

$\displaystyle A_2=\int ^2_1(2−x)dx=[2x−\dfrac{x^2}{2}]∣^2_1=\dfrac{1}{2}.$

Kuongeza maeneo haya pamoja, tunapata

$\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{5}{6}.$

Eneo la mkoa ni$\displaystyle 5/6$ vitengo ²^.

Zoezi$\PageIndex{4}$

Fikiria kanda iliyoonyeshwa katika takwimu zifuatazo. Kupata eneo la$\textbf{R}$.

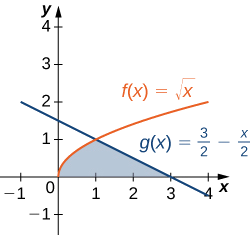
$Takwimu hii ina grafu mbili katika quadrant ya kwanza. Wao ni kazi f (x) = mraba wa x na g (x) = 3/2 - x/2. Kati ya grafu hizi ni eneo la kivuli, lililofungwa upande wa kushoto na f (x) na kulia kwa g (x). Yote ambayo ni juu ya x-axis. Eneo la kivuli ni kati ya x=0 na x=3.$

Kidokezo: Vipande viwili vinaingiliana katika x=1

Jibu: $\displaystyle \dfrac{5}{3}$vitengo ²

Mikoa Defined kwa Heshima y

Katika Mfano$\PageIndex{4}$, tulipaswa kutathmini integrals mbili tofauti ili kuhesabu eneo la kanda. Hata hivyo, kuna njia nyingine ambayo inahitaji moja tu muhimu. Nini kama sisi kutibu curves kama kazi ya$\displaystyle y$, badala ya kama kazi ya$\displaystyle x$? Tathmini Kielelezo. Kumbuka kuwa grafu ya kushoto, iliyoonyeshwa kwa nyekundu, inawakilishwa na kazi$\displaystyle y=f(x)=x^2$. Tunaweza tu kwa urahisi kutatua hili kwa x na kuwakilisha Curve na kazi$\displaystyle x=v(y)=\sqrt{y}$. (Kumbuka kuwa pia$\displaystyle x=−\sqrt{y}$ ni uwakilishi halali wa kazi$\displaystyle y=f(x)=x^2$ kama kazi ya$\displaystyle y$. Hata hivyo, kulingana na grafu, ni wazi tunavutiwa na mizizi nzuri ya mraba.) Vile vile, grafu sahihi inawakilishwa na kazi$\displaystyle y=g(x)=2−x$, lakini inaweza tu kwa urahisi kuwakilishwa na kazi$\displaystyle x=u(y)=2−y$. Wakati grafu zinawakilishwa kama kazi za$\displaystyle y$, tunaona kanda imefungwa upande wa kushoto na grafu ya kazi moja na upande wa kulia na grafu ya kazi nyingine. Kwa hiyo, ikiwa tunaunganisha kwa heshima$\displaystyle y$, tunahitaji kutathmini moja muhimu tu. Hebu tuendeleze formula ya aina hii ya ushirikiano.

Hebu$\displaystyle u(y)$ na$\displaystyle v(y)$ uwe na kazi zinazoendelea juu ya muda$\displaystyle [c,d]$ kama vile$\displaystyle u(y)≥v(y)$ kwa wote$\displaystyle y∈[c,d]$. Tunataka kupata eneo kati ya grafu ya kazi, kama inavyoonekana kwenye Kielelezo$\PageIndex{7}$.

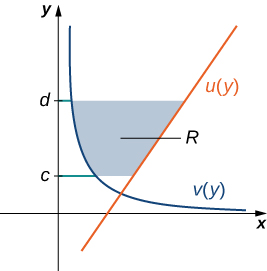
Takwimu hii ina grafu mbili katika quadrant ya kwanza. Wao ni kazi v (y) na u (y). Kati ya grafu hizi ni kanda kivuli, imepakana upande wa kushoto na v (y) na kulia na u (y). Eneo limeandikwa R. eneo la kivuli ni kati ya mipaka ya usawa ya y=c na y=d. — Kielelezo$\PageIndex{7}$: Tunaweza kupata eneo kati ya grafu ya kazi mbili,$\displaystyle u(y)$ na$\displaystyle v(y)$.

Wakati huu, tunakwenda kugawanya muda kwenye mhimili wa y na kutumia rectangles usawa ili takriban eneo kati ya kazi. Kwa hiyo, kwa$\displaystyle i=0,1,2,…,n$, basi$\displaystyle Q={y_i}$ iwe sehemu ya kawaida ya$\displaystyle [c,d]$. Kisha, kwa$\displaystyle i=1,2,…,n$, chagua hatua$\displaystyle y^∗_i∈[y_{i−1},y_i]$, kisha juu ya kila muda$\displaystyle [y_{i−1},y_i]$ ujenga mstatili unaoenea kwa usawa kutoka$\displaystyle v(y^0∗_i)$ kwa$\displaystyle u(y^∗_i)$. Kielelezo$\PageIndex{8a}$ kinaonyesha rectangles wakati$\displaystyle y^∗_i$ umechaguliwa kuwa mwisho wa chini wa muda na$\displaystyle n=10$. Kielelezo$\PageIndex{8b}$ kinaonyesha mstatili wa mwakilishi kwa undani.

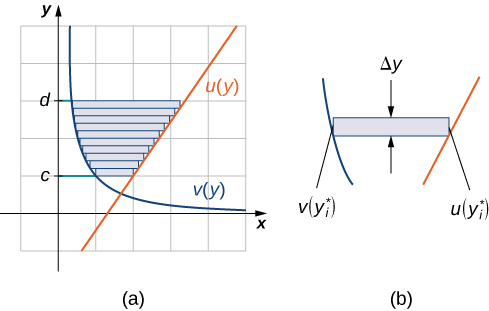
Takwimu hii ina grafu tatu. Takwimu ya kwanza ina curves mbili. Wao ni kazi v (y*) na u (y*). Kati ya curves hizi ni mstatili usawa. Takwimu ya pili iliyoandikwa “(a)”, ni kanda ya kivuli, imefungwa upande wa kushoto na v (y) na kulia na u (y). Eneo la kivuli ni kati ya mipaka ya usawa ya y=c na y=d. eneo hili la kivuli limevunjwa ndani ya mstatili kati ya curves. takwimu ya tatu, kinachoitwa “(b)”, ni curves mbili v (y*) na u (y*). Kati ya curves ni mstatili usawa na upana delta y. — Kielelezo$\PageIndex{8}$: (a) Kukadiria eneo kati ya grafu za kazi mbili,$\displaystyle u(y)$ na$\displaystyle v(y)$, na mstatili. (b) Eneo la mstatili wa kawaida.

Urefu wa kila mstatili wa mtu binafsi ni$\displaystyle Δy$ na upana wa kila mstatili ni$\displaystyle u(y^∗_i)−v(y^∗_i)$. Kwa hiyo, eneo kati ya curves ni takriban

\[ A≈\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy . \nonumber \]

Hii ni jumla Riemann, hivyo sisi kuchukua kikomo kama$\displaystyle n→∞,$ kupata

\[ \begin{align*} A =\lim_{n→∞}\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy \\[4pt] =\int ^d_c[u(y)−v(y)]dy. \end{align*}\]

Matokeo haya ni muhtasari katika theorem zifuatazo.

Kutafuta Eneo kati ya Curves mbili, Kuunganisha kando ya mhimili wa y

Hebu$\displaystyle u(y)$ na$\displaystyle v(y)$ uwe na kazi zinazoendelea kama hizo$\displaystyle u(y)≥v(y) $ kwa wote$\displaystyle y∈[c,d]$. Hebu$\textbf{R}$ kuashiria eneo lililofungwa upande wa kulia na grafu ya$\displaystyle u(y)$, upande wa kushoto na grafu ya$\displaystyle v(y)$, na juu na chini na mistari$\displaystyle y=d$ na$\displaystyle y=c$, kwa mtiririko huo. Kisha, eneo la$\textbf{R}$ hutolewa na

\[A=\int ^d_c[u(y)−v(y)]dy. \nonumber \]

Mfano$\PageIndex{5}$: Integrating with Respect to y

Hebu kupitia upya Mfano$\PageIndex{4}$, tu wakati huu hebu kuunganisha kwa heshima na$\displaystyle y$. Hebu$\textbf{R}$ kuwa kanda iliyoonyeshwa kwenye Kielelezo$\PageIndex{9}$. Kupata eneo la$\textbf{R}$ kwa kuunganisha kwa heshima na$\displaystyle y$.

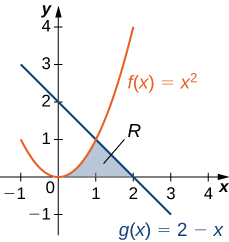
Suluhisho

Ni lazima kwanza kueleza grafu kama kazi ya$\displaystyle y$. Kama tulivyoona mwanzoni mwa sehemu hii, curve upande wa kushoto inaweza kuwakilishwa na kazi$\displaystyle x=v(y)=\sqrt{y}$, na curve upande wa kulia inaweza kuwakilishwa na kazi$\displaystyle x=u(y)=2−y$.

Sasa tunapaswa kuamua mipaka ya ushirikiano. Mkoa umepakana chini na x-axis, hivyo kikomo cha chini cha ushirikiano ni$\displaystyle y=0$. Kikomo cha juu cha ushirikiano kinatambuliwa na hatua ambapo grafu mbili zinaingiliana, ambayo ni hatua$\displaystyle (1,1)$, hivyo kikomo cha juu cha ushirikiano ni$\displaystyle y=1$. Hivyo, tuna$\displaystyle [c,d]=[0,1]$.

Kuhesabu eneo la kanda, tunapata

\[ \begin{align*} A =\int ^d_c[u(y)−v(y)]dy \\[4pt] =\int ^1_0[(2−y)−\sqrt{y}]dy\\[4pt] =[2y−\dfrac{y^2}{2}−\dfrac{2}{3}y^{3/2}]∣^1_0\\[4pt] =\dfrac{5}{6}. \end{align*}\]

Eneo la mkoa ni$\displaystyle 5/6$ vitengo ².

Zoezi$\PageIndex{5}$

Hebu tupate upya uhakiki unaohusishwa na Mfano$\PageIndex{4}$, wakati huu tu, hebu tuunganishe kwa heshima na$\displaystyle y$. Hebu$\textbf{R}$ kuwa kanda iliyoonyeshwa katika takwimu zifuatazo. Kupata eneo la$\textbf{R}$ kwa kuunganisha kwa heshima na$\displaystyle y$.

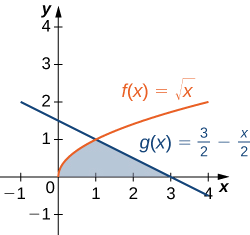
Kidokezo: Fuata mchakato kutoka kwa mfano uliopita.

Jibu: $\displaystyle \dfrac{5}{3}$vitengo ²

Dhana muhimu

Kama vile integrals uhakika inaweza kutumika kupata eneo chini ya curve, wanaweza pia kutumika kupata eneo kati ya curves mbili.
Ili kupata eneo kati ya curves mbili zilizoelezwa na kazi, kuunganisha tofauti ya kazi.
Ikiwa grafu za kazi zinavuka, au ikiwa kanda ni ngumu, tumia thamani kamili ya tofauti ya kazi. Katika kesi hii, inaweza kuwa muhimu kutathmini integrals mbili au zaidi na kuongeza matokeo ili kupata eneo la kanda.
Wakati mwingine inaweza kuwa rahisi kuunganisha kwa heshima na y kupata eneo hilo. Kanuni hizo ni sawa bila kujali ni variable gani hutumiwa kama variable ya ushirikiano.

Mlinganyo muhimu

Eneo kati ya curves mbili, kuunganisha kwenye x-axis

$\displaystyle A=\int ^b_a[f(x)−g(x)]dx$

Eneo kati ya curves mbili, kuunganisha kwenye mhimili wa y

$\displaystyle A=\int ^d_c[u(y)−v(y)]dy$

Kupata Eneo kati ya Curves mbili

Mfano\(\PageIndex{1}\): Finding the Area of a Region between Two Curves I

Zoezi\(\PageIndex{1}\)

Mfano\(\PageIndex{2}\): Finding the Area of a Region between Two Curves II

Zoezi\(\PageIndex{2}\)

Kutafuta Eneo la Mkoa kati ya Curves Hiyo Msalaba

Mfano\(\PageIndex{3}\): Finding the Area of a Region Bounded by Functions That Cross

Zoezi\(\PageIndex{3}\)

Mfano\(\PageIndex{4}\): Finding the Area of a Complex Region

Zoezi\(\PageIndex{4}\)

Kutafuta Eneo kati ya Curves mbili, Kuunganisha kando ya mhimili wa y

Mfano\(\PageIndex{5}\): Integrating with Respect to y

Zoezi\(\PageIndex{5}\)