5.6: Integrals Kuhusisha Kielelezo na Logarithmic Kazi
- Page ID
- 178554
- Unganisha kazi zinazohusisha kazi za kielelezo.
- Unganisha kazi zinazohusisha kazi za logarithmic.
Kazi za kielelezo na logarithmic hutumiwa kutengeneza ukuaji wa idadi ya watu, ukuaji wa seli, na ukuaji wa fedha, pamoja na kushuka kwa thamani, kuoza kwa mionzi, na matumizi ya rasilimali, kwa jina la maombi machache tu. Katika sehemu hii, sisi kuchunguza ushirikiano kuwashirikisha kazi kielelezo na logarithmic.
Integrals ya Kazi Kielelezo
Kazi ya ufafanuzi ni labda kazi yenye ufanisi zaidi katika suala la shughuli za calculus. Kazi ya kielelezo,\(y=e^x\), ni derivative yake mwenyewe na muhimu yake mwenyewe.
Kazi za kielelezo zinaweza kuunganishwa kwa kutumia formula zifuatazo.
\[ \begin{align} ∫e^x\,dx &= e^x+C \\[4pt] ∫a^x\,dx &=\dfrac{a^x}{\ln a}+C \end{align} \nonumber \]
Pata antiderivative ya kazi ya kielelezo\(e^{−x}\).
Suluhisho
Tumia ubadilishaji, kuweka\(u=−x,\) na kisha\(du=−1\,dx\). Kuzidisha\(du\) equation na\(−1\), hivyo sasa una\(−du=\,dx\). Kisha,
\[∫e^{−x}\,dx=−∫e^u\,du=−e^u+C=−e^{−x}+C. \nonumber \]
Pata antiderivative ya kazi kwa kutumia mbadala:\(x^2e^{−2x^3}\).
- Kidokezo
-
Hebu\(u\) sawa exponent juu ya\(e\).
- Jibu
-
\(\displaystyle ∫x^2e^{−2x^3}\,dx=−\dfrac{1}{6}e^{−2x^3}+C\)
Hitilafu ya kawaida wakati wa kushughulika na maneno ya kielelezo ni kutibu kielelezo\(e\) kwa njia ile ile tunayotendea vielelezo katika maneno ya polynomial. Hatuwezi kutumia utawala wa nguvu kwa exponent juu\(e\). Hii inaweza kuwa hasa utata wakati tuna wote exponentials na polynomials katika kujieleza huo, kama katika checkpoint uliopita. Katika kesi hizi, tunapaswa daima mara mbili-kuangalia ili kuhakikisha sisi ni kutumia sheria sahihi kwa ajili ya kazi sisi ni kuunganisha.
Pata antiderivative ya kazi ya kielelezo\(e^x\sqrt{1+e^x}\).
Suluhisho
Kwanza kuandika upya tatizo kwa kutumia exponent busara:
\[∫e^x\sqrt{1+e^x}\,dx=∫e^x(1+e^x)^{1/2}\,dx.\nonumber \]
Kutumia mbadala, chagua\(u=1+e^x\). Kisha,\(du=e^x\,dx\). Tuna
\[∫e^x(1+e^x)^{1/2}\,dx=∫u^{1/2}\,du.\nonumber \]
Kisha
\[∫u^{1/2}\,du=\dfrac{u^{3/2}}{3/2}+C=\dfrac{2}{3}u^{3/2}+C=\dfrac{2}{3}(1+e^x)^{3/2}+C\nonumber \]
![Grafu ya kazi f (x) = e ^ x * sqrt (1 + e ^ x), ambayo ni kuongezeka concave up Curve, juu ya [-3, 1]. Inaanza karibu na mhimili x katika roboduara mbili, huvuka mhimili y kwenye (0, sqrt (2)), na inaendelea kuongezeka kwa kasi.](https://math.libretexts.org/@api/deki/files/12432/5.6.1.png)
Kupata antiderivative ya\(e^x(3e^x−2)^2\).
- Kidokezo
-
Hebu\(u=3e^x−2\).
- Jibu
-
\(\displaystyle ∫e^x(3e^x−2)^2\,dx=\dfrac{1}{9}(3e^x−2)^3+C\)
Matumizi badala ya kutathmini muhimu kwa muda usiojulikana\(\displaystyle ∫3x^2e^{2x^3}\,dx.\)
Suluhisho
Hapa sisi kuchagua basi\(u\) sawa kujieleza katika exponent juu\(e\). Hebu\(u=2x^3\) na\(du=6x^2\,dx\). Kwa mara nyingine tena,\(du\) ni mbali na multiplier mara kwa mara; kazi ya awali ina sababu ya\(3x^2,\) si\(6x^2\). Kuzidisha pande zote mbili za equation na\(\dfrac{1}{2}\) ili integrand katika\(u\) sawa integrand katika\(x\). Hivyo,
\[∫3x^2e^{2x^3}\,dx=\frac{1}{2}∫e^u\,du. \nonumber \]
Kuunganisha kujieleza katika\(u\) na kisha mbadala kujieleza awali katika\(x\) nyuma katika\(u\) -muhimu:
\[\frac{1}{2}∫e^u\,du=\frac{1}{2}e^u+C=\frac{1}{2}e^2x^3+C. \nonumber \]
Tathmini muhimu ya muda usiojulikana\(\displaystyle ∫2x^3e^{x^4}\,dx\).
- Kidokezo
-
Hebu\(u=x^4.\)
- Jibu
-
\(\displaystyle ∫2x^3e^{x^4}\,dx=\frac{1}{2}e^{x^4}+C\)
Kama ilivyoelezwa mwanzoni mwa sehemu hii, kazi za kielelezo zinatumiwa katika programu nyingi za maisha halisi. Idadi mara nyingi\(e\) huhusishwa na ukuaji wa mchanganyiko au kuharakisha, kama tulivyoona katika sehemu za awali kuhusu derivative. Ingawa derivative inawakilisha kiwango cha mabadiliko au kiwango cha ukuaji, muhimu inawakilisha mabadiliko ya jumla au ukuaji wa jumla. Hebu tuangalie mfano ambao ushirikiano wa kazi ya kielelezo hutatua maombi ya kawaida ya biashara.
Kazi ya mahitaji ya bei-inatuambia uhusiano kati ya wingi wa bidhaa zinazohitajika na bei ya bidhaa. Kwa ujumla, bei itapungua kadiri ongezeko la kiasi kinachohitajika. Kando bei-mahitaji kazi ni derivative ya bei-mahitaji kazi na inatuambia jinsi ya haraka mabadiliko ya bei katika ngazi fulani ya uzalishaji. Kazi hizi hutumiwa katika biashara ili kuamua bei-elasticity ya mahitaji, na kusaidia makampuni kuamua kama kubadilisha viwango vya uzalishaji itakuwa faida.
Kupata bei-mahitaji equation kwa brand fulani ya dawa ya meno katika mlolongo maduka makubwa wakati mahitaji ni\(50\) zilizopo kwa wiki katika $2.35 kwa tube, kutokana na kwamba pembezoni bei-mahitaji kazi,\(p′(x),\) kwa\(x\) idadi ya zilizopo kwa wiki, ni kutolewa kama
\[p'(x)=−0.015e^{−0.01x}. \nonumber \]
Ikiwa mlolongo wa maduka makubwa huuza\(100\) zilizopo kwa wiki, ni bei gani inapaswa kuweka?
Suluhisho
Ili kupata equation bei-mahitaji, kuunganisha pembezoni bei-mahitaji kazi. Kwanza kupata antiderivative, kisha angalia maelezo. Hivyo,
\[p(x)=∫−0.015e^{−0.01x}\,dx=−0.015∫e^{−0.01x}\,dx. \nonumber \]
Kutumia mbadala, basi\(u=−0.01x\) na\(du=−0.01\,dx\). Kisha, kugawanya pande zote mbili za\(du\) equation na\(−0.01\). Hii inatoa
\[\dfrac{−0.015}{−0.01}∫e^u\,du=1.5∫e^u\,du=1.5e^u+C=1.5e^{−0.01}x+C. \nonumber \]
Hatua inayofuata ni kutatua\(C\). Tunajua kwamba wakati bei ni $2.35 kwa tube, mahitaji ni\(50\) zilizopo kwa wiki. Hii ina maana
\[p(50)=1.5e^{−0.01(50)}+C=2.35. \nonumber \]
Sasa, tu kutatua kwa\(C\):
\[C=2.35−1.5e^{−0.5}=2.35−0.91=1.44. \nonumber \]
Hivyo,
\[p(x)=1.5e^{−0.01x}+1.44. \nonumber \]
Kama maduka makubwa anauza\(100\) zilizopo ya dawa ya meno kwa wiki, bei itakuwa
\[p(100)=1.5e−0.01(100)+1.44=1.5e−1+1.44≈1.99. \nonumber \]
Maduka makubwa yanapaswa kulipa $1.99 kwa tube ikiwa inauza\(100\) zilizopo kwa wiki.
Tathmini muhimu ya uhakika\(\displaystyle ∫^2_1e^{1−x}\,dx.\)
Suluhisho
Tena, badala ni njia ya kutumia. Hebu\(u=1−x,\) hivyo\(\,du=−1\,dx\) au\(−\,du=\,dx\). Kisha\(\displaystyle ∫e^{1−x}\,dx=−∫e^u\,du.\)
Kisha, mabadiliko ya mipaka ya ushirikiano. Kutumia equation\(u=1−x\), tuna:
\[\text{When }x = 1, \quad u=1−(1)=0, \nonumber \]
\[\text{and when }x = 2, \quad u=1−(2)=−1. \nonumber \]
Muhimu basi inakuwa
\[\begin{align*} ∫^2_1e^{1−x}\,\,dx &= −∫^{−1}_0e^u\,\,du \\[4pt] &=∫^0_{−1}e^u\,\,du \\[4pt] &=e^u\bigg|^0_{−1}=e^0−(e^{−1}) \\[4pt] &=−e^{−1}+1. \end{align*}\]
Angalia Kielelezo\(\PageIndex{2}\).
![Grafu ya kazi f (x) = e^ (1-x) juu ya [0, 3]. Ni misalaba y mhimili katika (0, e) kama kupungua concave up Curve na symptotically mbinu 0 kama x inakwenda infinity.](https://math.libretexts.org/@api/deki/files/12433/5.6.2.png)
Tathmini\(\displaystyle ∫^2_0e^{2x}\,dx.\)
- Kidokezo
-
Hebu\(u=2x.\)
- Jibu
-
\(\displaystyle \frac{1}{2}∫^4_0e^u\,du=\dfrac{1}{2}(e^4−1)\)
Tuseme kiwango cha ukuaji wa bakteria katika sahani ya Petri hutolewa na\(q(t)=3^t\), ambapo\(t\) hutolewa kwa masaa na\(q(t)\) hutolewa kwa maelfu ya bakteria kwa saa. Ikiwa utamaduni huanza na\(10,000\) bakteria, tafuta kazi\(Q(t)\) ambayo inatoa idadi ya bakteria katika sahani ya Petri wakati wowote\(t\). Ni bakteria ngapi katika sahani baada ya\(2\) masaa?
Suluhisho
Tuna
\[Q(t)=∫3^tdt=\dfrac{3^t}{\ln 3}+C. \nonumber \]
Kisha, saa\(t=0\) tuna\(Q(0)=10=\dfrac{1}{\ln 3}+C,\) hivyo\(C≈9.090\) na sisi kupata
\[Q(t)=\dfrac{3^t}{\ln 3}+9.090. \nonumber \]
Kwa wakati\(t=2\), tuna
\[\begin{align*} Q(2) &=\dfrac{3^2}{\ln 3}+9.090 \\[4pt] &\approx 17.282. \end{align*}\]
Baada ya masaa 2, kuna bakteria 17,282 katika sahani.
Kutoka Mfano, tuseme bakteria kukua kwa kiwango cha\(q(t)=2^t\). Fikiria utamaduni bado huanza na\(10,000\) bakteria. Kupata\(Q(t)\). Ni bakteria ngapi katika sahani baada ya\(3\) masaa?
- Kidokezo
-
Tumia utaratibu kutoka kwa Mfano\(\PageIndex{6}\) ili kutatua tatizo
- Jibu
-
\[\begin{align*} Q(t) &= \dfrac{2^t}{\ln 2} + 8.557. \\[4pt] Q(3) &\approx 20,099 \end{align*}\]
Kwa hiyo kuna\(20,099\) bakteria katika sahani baada ya\(3\) masaa.
Tuseme idadi ya nzizi za matunda huongezeka kwa kiwango cha\(g(t)=2e^{0.02t}\), kwa nzizi kwa siku. Ikiwa idadi ya awali ya nzizi za matunda ni\(100\) nzi, ni nzizi ngapi katika idadi ya watu baada ya\(10\) siku?
Suluhisho
Hebu\(G(t)\) kuwakilisha idadi ya nzizi katika idadi ya watu kwa wakati\(t\). Kutumia theorem ya mabadiliko ya wavu, tuna
\[ \begin{align*} G(10)=G(0)+∫^{10}_02e^{0.02t}\,dt \\[4pt] &=100+\left[\dfrac{2}{0.02}e^{0.02t}\right]∣^{10}_0 \\[4pt] &=100+\left[100e^{0.02t}\right]∣^{10}_0 \\[4pt] &=100+100e^{0.2}−100 \\[4pt] &≈122. \end{align*}\]
Kuna\(122\) nzizi katika idadi ya watu baada ya\(10\) siku.
Tuseme kiwango cha ukuaji wa idadi ya watu wa kuruka hutolewa\(g(t)=e^{0.01t},\) na idadi ya kwanza ya kuruka ni\(100\) nzi. Ni nzizi ngapi katika idadi ya watu baada ya\(15\) siku?
- Kidokezo
-
Tumia mchakato kutoka Mfano\(\PageIndex{7}\) ili kutatua tatizo.
- Jibu
-
Kuna\(116\) nzizi.
Tathmini muhimu ya uhakika kwa kutumia mbadala:\[∫^2_1\dfrac{e^{1/x}}{x^2}\,dx.\nonumber \]
Suluhisho
Tatizo hili linahitaji kuandika upya ili kurahisisha kutumia mali. Kwanza, kuandika upya exponent juu ya e kama nguvu ya\(x\), kisha kuleta\(x^2\) katika denominator hadi nambari kwa kutumia exponent hasi. Tuna
\[∫^2_1\dfrac{e^{1/x}}{x^2}\,\,dx=∫^2_1e^{x^{−1}}x^{−2}\,dx. \nonumber \]
Hebu\(u=x^{−1},\) exponent juu ya\(e\). Kisha
\[du=−x^{−2}\,dx \nonumber \]
\[−du=x^{−2}\,dx. \nonumber \]
Kuleta ishara hasi nje ya ishara muhimu, tatizo sasa linasoma
\[−∫e^u\,du. \nonumber \]
Kisha, mabadiliko ya mipaka ya ushirikiano:
\[u=(1)^{−1}=1 \nonumber \]
\[u=(2)^{−1}=\dfrac{1}{2}. \nonumber \]
Kumbuka kwamba sasa mipaka huanza na idadi kubwa, maana tunaweza kuzidisha\(−1\) na kubadilishana mipaka. Hivyo,
\[−∫^{1/2}_1e^u\,du=∫^1_{1/2}e^u\,du=e^u\big|^1_{1/2}=e−e^{1/2}=e−\sqrt{e}.\nonumber \]
Tathmini muhimu ya uhakika kwa kutumia mbadala:\[∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}\,dx.\nonumber \]
- Kidokezo
-
Hebu\(u=4x^{−2}.\)
- Jibu
-
\(\displaystyle ∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}\,dx=\dfrac{1}{8}[e^4−e]\).
Integrals Kuhusisha Kazi Logarithmic
Kuunganisha kazi za\(f(x)=x^{−1}\) matokeo ya fomu kwa thamani kamili ya kazi ya logi ya asili, kama inavyoonekana katika utawala wafuatayo. Fomu muhimu kwa kazi nyingine za logarithmic, kama vile\(f(x)=\ln x\) na\(f(x)=\log_a x\), pia zinajumuishwa katika utawala.
Fomu zifuatazo zinaweza kutumika kutathmini integrals zinazohusisha kazi za logarithmic.
\[\begin{align*} ∫x^{−1}\,dx &=\ln |x|+C \\[4pt] ∫\ln x\,\,dx &= x\ln x−x+C =x (\ln x−1)+C \\[4pt] ∫\log_a x\,dx &=\dfrac{x}{\ln a}(\ln x−1)+C \end{align*}\]
Pata antiderivative ya kazi\(\dfrac{3}{x−10}. \)
Suluhisho
Sababu ya kwanza\(3\) nje ishara muhimu. Kisha utumie\(u^{−1}\) utawala. Hivyo,
\[∫\dfrac{3}{x−10}\,dx=3∫\dfrac{1}{x−10}\,dx=3∫\dfrac{du}{u}=3\ln |u|+C=3\ln |x−10|+C,\quad x≠10. \nonumber \]
Angalia Kielelezo\(\PageIndex{3}\).
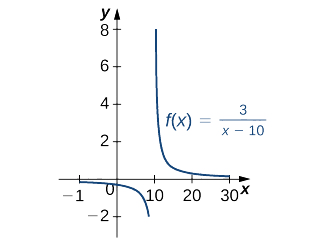
Kupata antiderivative ya\(\dfrac{1}{x+2}.\)
- Kidokezo
-
Fuata mfano kutoka Mfano\(\PageIndex{9}\) ili kutatua tatizo.
- Jibu
-
\(\displaystyle \int \dfrac{1}{x+2}\,dx = \ln |x+2|+C\)
Kupata antiderivative ya\(\dfrac{2x^3+3x}{x^4+3x^2}. \)
Suluhisho
Hii inaweza kuandikwa upya kama\(\displaystyle ∫(2x^3+3x)(x^4+3x^2)^{−1}\,dx.\) Matumizi badala.
Hebu\(u=x^4+3x^2\), kisha\(du=(4x^3+6x)\,dx.\) Badilisha\(du\) kwa factoring nje\(2\). Hivyo,
\[du=(4x^3+6x)\,dx=2(2x^3+3x)\,dx \nonumber \]
\[\dfrac{1}{2}\,du=(2x^3+3x)\,dx. \nonumber \]
Andika upya kiungo katika\(u\):
\[∫(2x^3+3x)(x^4+3x^2)^{−1}\,dx=\dfrac{1}{2}∫u^{−1}\,du. \nonumber \]
Kisha tuna
\[\dfrac{1}{2}∫u^{−1}\,du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln ∣x^4+3x^2∣+C. \nonumber \]
Pata antiderivative ya kazi ya logi\(\log_2 x.\)
Suluhisho
Fuata muundo katika formula iliyoorodheshwa katika utawala juu ya formula za ushirikiano zinazohusisha kazi za logarithmic. Kulingana na muundo huu, tuna
\[∫\log_2 x\,dx=\dfrac{x}{\ln 2}(\ln x−1)+C.\nonumber \]
Kupata antiderivative ya\(\log_3 x\).
- Kidokezo
-
Fuata Mfano\(\PageIndex{11}\) na rejea utawala juu ya formula za ushirikiano zinazohusisha kazi za logarithmic.
- Jibu
-
\(\displaystyle ∫\log_3 x\,dx=\dfrac{x}{\ln 3}(\ln x−1)+C\)
Mfano\(\PageIndex{12}\) ni muhimu muhimu ya kazi ya trigonometric. Kwa kazi za trigonometric, mara nyingi tunapaswa kutumia mali ya trigonometric au utambulisho kabla hatuwezi kuendelea. Kupata fomu sahihi ya integrand ni kawaida muhimu kwa ushirikiano laini.
Tathmini muhimu ya uhakika\[∫^{π/2}_0\dfrac{\sin x}{1+\cos x}\,dx.\nonumber \]
Suluhisho
Tunahitaji badala ya kutathmini tatizo hili. Hebu\(u=1+\cos x\) hivyo\(du=−\sin x\,\,dx.\)
Andika upya muhimu katika suala la\(u\), kubadilisha mipaka ya ushirikiano pia. Hivyo,
\[ \begin{align*} u &= 1+\cos(0)=2 \\[4pt] u &=1+\cos \left(\dfrac{π}{2}\right)=1.\end{align*}\]
Kisha
\[ \begin{align*}∫^{π/2}_0\dfrac{\sin x}{1+\cos x} &=−∫^1_2 u^{−1}\,du \\[4pt] &=∫^2_1u^{−1}\,du \\[4pt] &=\ln |u|\,\bigg|^2_1 \\[4pt] &=[\ln 2−\ln 1]=\ln 2 \end{align*}\]
Dhana muhimu
- Kazi za kielelezo na za logarithmic zinatokea katika programu nyingi za ulimwengu halisi, hasa zile zinazohusisha ukuaji na kuoza.
- Kubadilishwa mara nyingi hutumiwa kutathmini integrals zinazohusisha kazi za kielelezo au logarithms.
Mlinganyo muhimu
- Integrals ya Kazi Kielelezo
\[∫e^x\,dx=e^x+C \nonumber \]
\[\int a^x\,dx=\dfrac{a^x}{\ln a}+C \nonumber \]
- Fomu za ushirikiano zinazohusisha Kazi za Logarithmi
\[∫x^{−1}\,dx=\ln |x|+C \nonumber \]
\[∫\ln x\,dx=x\ln x−x+C=x(\ln x−1)+C \nonumber \]
\[∫\log_a x\,dx=\dfrac{x}{\ln a}(\ln x−1)+C \nonumber \]


