5.5E: Mazoezi ya Sehemu ya 5.5

1) Kwa nini\(u\) -badala inajulikana kama mabadiliko ya kutofautiana?

2) Ikiwa\( f=g∘h\), wakati wa kugeuza utawala wa mnyororo\(\dfrac{d}{dx}(g∘h)(x)=g′(h(x))h′(x)\), unapaswa kuchukua\( u=g(x)\) au\(u=h(x)?\)

Jibu

\(u=h(x)\)

Katika mazoezi 3 - 7, kuthibitisha kila utambulisho kwa kutumia tofauti. Kisha, kwa kutumia\(u\) ubadilishaji ulioonyeshwa,\(f\) tambua vile vile muhimu huchukua fomu\(\displaystyle∫f(u)\,du.\)

3)\(\displaystyle ∫x\sqrt{x+1}\,dx=\frac{2}{15}(x+1)^{3/2}(3x−2)+C;\quad u=x+1\)

4)\(\displaystyle∫\frac{x^2}{\sqrt{x−1}}\,dx=\frac{2}{15}\sqrt{x−1}(3x^2+4x+8)+C,\quad (x>1);\quad u=x−1\)

Jibu

\( f(u)=\dfrac{(u+1)^2}{\sqrt{u}}\)

5)\(\displaystyle∫x\sqrt{4x^2+9}\,dx=\frac{1}{12}(4x^2+9)^{3/2}+C;\quad u=4x^2+9\)

6)\(\displaystyle∫\frac{x}{\sqrt{4x^2+9}}\,dx=\frac{1}{4}\sqrt{4x^2+9}+C;\quad u=4x^2+9\)

Jibu

\( du=8x\,dx;\quad f(u)=\frac{1}{8\sqrt{u}}\)

7)\(\displaystyle∫\frac{x}{(4x^2+9)^2}\,dx=−\frac{1}{8(4x^2+9)} + C;\quad u=4x^2+9\)

Katika mazoezi 8 - 17, pata antiderivative kwa kutumia ubadilishaji ulioonyeshwa.

8)\(\displaystyle∫(x+1)^4\,dx;\quad u=x+1\)

Jibu

\(\displaystyle∫(x+1)^4\,dx = \frac{1}{5}(x+1)^5+C\)

9)\(\displaystyle∫(x−1)^5\,dx;\quad u=x−1\)

10)\(\displaystyle∫(2x−3)^{−7}\,dx;\quad u=2x−3\)

Jibu

\(\displaystyle∫(2x−3)^{−7}\,dx = −\frac{1}{12(2x−3)^6}+C\)

11)\(\displaystyle∫(3x−2)^{−11}\,dx;\quad u=3x−2\)

12)\(\displaystyle∫\frac{x}{\sqrt{x^2+1}}\,dx;\quad u=x^2+1\)

Jibu

\(\displaystyle∫\frac{x}{\sqrt{x^2+1}}\,dx = \sqrt{x^2+1}+C\)

13)\(\displaystyle∫\frac{x}{\sqrt{1−x^2}}\,dx;\quad u=1−x^2\)

14)\(\displaystyle∫(x−1)(x^2−2x)^3\,dx;\quad u=x^2−2x\)

Jibu

\(\displaystyle∫(x−1)(x^2−2x)^3\,dx = \frac{1}{8}(x^2−2x)^4+C\)

15)\(\displaystyle∫(x^2−2x)(x^3−3x^2)^2\,dx;\quad u=x^3=3x^2\)

16)\(\displaystyle∫\cos^3 θ\,dθ;\quad u=\sin θ\) (Kidokezo:\(\cos^2 θ=1−\sin^2 θ\))

Jibu

\(\displaystyle∫\cos^3 θ\,dθ = \sin θ−\dfrac{\sin^3 θ}{3}+C\)

17)\(\displaystyle ∫\sin^3 θ\,dθ;\quad u=\cos θ\) (Kidokezo:\(\sin^2 θ=1−\cos^2θ\))

Katika mazoezi 18 - 34, tumia mabadiliko ya kufaa ya vigezo ili kuamua muhimu kwa muda usiojulikana.

18)\(\displaystyle∫x(1−x)^{99}\,dx\)

Jibu

\ (\ kuanza {align*}\ displaystylex (1,1-x) ^ {99}\, dx &=\ Frac {(1,1-x) ^ {101}} {101} -\ Frac {(1,1-x) ^ {100}} {100}} {100} +C\\ [4pt]
&=-\ frac {(1-x) ^ {100}} {10100}\ kubwa [100x + 1\ kubwa] +C\ mwisho {align*}\)

19)\(\displaystyle∫t(1−t^2)^{10}dt\)

20)\(\displaystyle∫(11x−7)^{−3}\,dx\)

Jibu

\(\displaystyle∫(11x−7)^{−3}\,dx = −\frac{1}{22(11x−7)^2}+C\)

21)\(\displaystyle∫(7x−11)^4\,dx\)

22)\(\displaystyle∫\cos^3 θ\sin θ\,dθ\)

Jibu

\(\displaystyle∫\cos^3 θ\sin θ\,dθ = −\frac{\cos^4 θ}{4}+C\)

23)\(\displaystyle∫\sin^7 θ\cos θ\,dθ\)

24)\(\displaystyle∫\cos^2(πt)\sin(πt)\,dt\)

Jibu

\(\displaystyle∫\cos^2(πt)\sin(πt)\,dt = −\frac{cos^3(πt)}{3π}+C\)

25)\(\displaystyle∫\sin^2 x\cos^3 x\,dx\) (Kidokezo:\(\sin^2 x+\cos^2 x=1\))

26)\(\displaystyle∫t\sin(t^2)\cos(t^2)\,dt\)

Jibu

\(\displaystyle∫t\sin(t^2)\cos(t^2)\,dt = −\frac{1}{4}\cos^2(t^2)+C\)

27)\(\displaystyle∫t^2\cos^2(t^3)\sin(t^3)\,dt\)

28)\(\displaystyle∫\frac{x^2}{(x^3−3)^2}\,dx\)

Jibu

\(\displaystyle∫\frac{x^2}{(x^3−3)^2}\,dx = −\frac{1}{3(x^3−3)}+C\)

29)\(\displaystyle∫\frac{x^3}{\sqrt{1−x^2}}\,dx\)

30)\(\displaystyle∫\frac{y^5}{(1−y^3)^{3/2}}\,dy\)

Jibu

\(\displaystyle∫\frac{y^5}{(1−y^3)^{3/2}}\,dy = −\frac{2(y^3−2)}{3\sqrt{1−y^3}}+C\)

31)\(\displaystyle∫\cos θ(1−\cos θ)^{99}\sin θ\,dθ\)

32)\(\displaystyle∫(1−\cos^3 θ)^{10}\cos^2 θ\sin θ\,dθ\)

Jibu

\(\displaystyle∫(1−\cos^3 θ)^{10}\cos^2 θ\sin θ\,dθ = \frac{1}{33}(1−\cos^3 θ)^{11}+C\)

33)\(\displaystyle∫(\cos θ−1)(\cos^2 θ−2\cos θ)^3\sin θ\,dθ\)

34)\(\displaystyle∫(\sin^2 θ−2\sin θ)(\sin^3 θ−3\sin^2 θ)^3\cos θ\,dθ\)

Jibu

\(\displaystyle∫(\sin^2 θ−2\sin θ)(\sin^3 θ−3\sin^2 θ)^3\cos θ\,dθ = \frac{1}{12}(\sin^3 θ−3\sin^2 θ)^4+C\)

Katika mazoezi ya 35 - 38, tumia calculator kukadiria eneo chini ya pembe kwa kutumia jumla ya Riemann ya kushoto na maneno 50, halafu utumie badala ya kutatua jibu halisi.

35) [T]\(y=3(1−x)^2\) juu\([0,2]\)

36) [T]\(y=x(1−x^2)^3\) juu\([−1,2]\)

Jibu

\(L_{50}=−8.5779.\)Eneo halisi ni\(\frac{−81}{8}\) vitengo\(^2\).

37) [T]\(y=\sin x(1−\cos x)^2\) juu\([0,π]\)

38) [T]\(y=\dfrac{x}{(x^2+1)^2}\) juu\([−1,1]\)

Jibu

\(L_{50}=−0.006399\). Eneo halisi ni 0.

Katika mazoezi 39 - 44, tumia mabadiliko ya vigezo ili kutathmini muhimu.

39)\(\displaystyle∫^1_0x\sqrt{1−x^2}\,dx\)

40)\(\displaystyle∫^1_0\frac{x}{\sqrt{1+x^2}}\,dx\)

Jibu

\(\displaystyle u=1+x^2,\quad du=2x\,dx,\quad ∫^1_0\frac{x}{\sqrt{1+x^2}}\,dx = \frac{1}{2}∫^2_1u^{−1/2}du=\sqrt{2}−1\)

41)\(\displaystyle∫^2_0\frac{t}{\sqrt{5+t^2}}\,dt\)

42)\(\displaystyle∫^1_0\frac{t^2}{\sqrt{1+t^3}}\,dt\)

Jibu

\(\displaystyle u=1+t^3,\quad du=3t^2,\quad ∫^1_0\frac{t^2}{\sqrt{1+t^3}}\,dt = \frac{1}{3}∫^2_1u^{−1/2}du=\frac{2}{3}(\sqrt{2}−1)\)

43)\(\displaystyle∫^{π/4}_0\sec^2 θ\tan θ\,dθ\)

44)\(\displaystyle∫^{π/4}_0\frac{\sin θ}{\cos^4 θ}\,dθ\)

Jibu

\(\displaystyle u=\cos θ,\quad du=−\sin θ\,dθ,\quad \int^{π/4}_0\frac{\sin θ}{\cos^4 θ}\,dθ = -∫_1^{\sqrt{2}/2}u^{−4}\,du = ∫^1_{\sqrt{2}/2}u^{−4}\,du=\frac{1}{3}(2\sqrt{2}−1)\)

Katika mazoezi 45 - 50, tathmini muhimu isiyo na kipimo\(\displaystyle ∫f(x)\,dx\) na\(C=0\) matumizi ya mara kwa mara\(u\) -badala. Kisha, graph kazi na antiderivative juu ya muda ulioonyeshwa. Ikiwezekana, makadirio ya thamani ya\(C\) kwamba ingehitaji kuongezwa kwa antiderivative ili kuifanya sawa na muhimu ya uhakika\(\displaystyle F(x)=∫^x_af(t)\,dt\), na mwisho wa kushoto wa muda uliopewa.

45) [T]\(\displaystyle∫(2x+1)e^{x^2+x−6}\,dx\) juu\([−3,2]\)

46) [T]\(\displaystyle∫\frac{\cos(\ln(2x))}{x}\,dx\) juu\([0,2]\)

Jibu

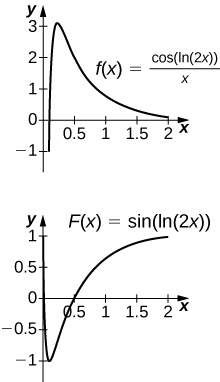
Antiderivative ni\(y=\sin(\ln(2x))\). Kwa kuwa antiderivative si kuendelea katika\(x=0\), mtu hawezi kupata thamani ya C ambayo kufanya\(y=\sin(\ln(2x))−C\) kazi kama muhimu uhakika.

47) [T]\(\displaystyle ∫\frac{3x^2+2x+1}{\sqrt{x^3+x^2+x+4}}\,dx\) juu\([−1,2]\)

48) [T]\(\displaystyle ∫\frac{\sin x}{\cos^3x}\,dx\) juu\(\left[−\frac{π}{3},\frac{π}{3}\right]\)

Jibu

Antiderivative ni\(y=\frac{1}{2}\sec^2 x\). Unapaswa kuchukua\(C=−2\) ili\(F(−\frac{π}{3})=0.\)

49) [T]\(\displaystyle ∫(x+2)e^{−x^2−4x+3}\,dx\) juu\([−5,1]\)

50) [T]\(\displaystyle ∫3x^2\sqrt{2x^3+1}\,dx\) juu\([0,1]\)

Jibu

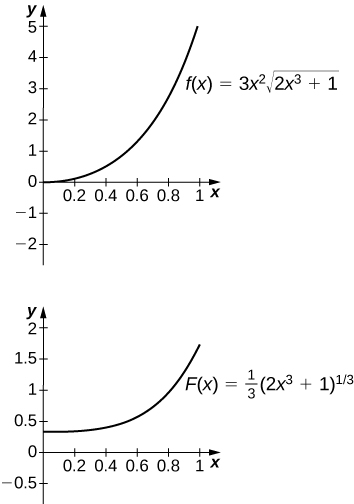
Antiderivative ni\( y=\frac{1}{3}(2x^3+1)^{3/2}\). Mtu anapaswa kuchukua\(C=−\frac{1}{3}\).

51) Ikiwa\(h(a)=h(b)\) unaweza kusema\(\displaystyle ∫^b_ag'(h(x))h(x)\,dx,\) nini kuhusu thamani ya muhimu?

52) Je, badala\(u=1−x^2\) ya uhakika muhimu ni\(\displaystyle ∫^2_0\frac{x}{1−x^2}\,dx\) sawa? Ikiwa sio, kwa nini?

Jibu

Hapana, kwa sababu integrand ni discontinuous katika\(x=1\).

Katika mazoezi 53 - 59, tumia mabadiliko ya vigezo ili kuonyesha kwamba kila muhimu ya uhakika ni sawa na sifuri.

53)\(\displaystyle ∫^π_0\cos^2(2θ)\sin(2θ)\,dθ\)

54)\(\displaystyle ∫^\sqrt{π}_0t\cos(t^2)\sin(t^2)\,dt\)

Jibu

\(u=\sin(t^2);\)muhimu inakuwa\(\displaystyle \frac{1}{2}∫^0_0u\,du.\)

55)\(\displaystyle ∫^1_0(1−2t)\,dt\)

56)\(\displaystyle ∫^1_0\frac{1−2t}{1+(t−\frac{1}{2})^2}\,dt\)

Jibu

\(u=1+(t−\frac{1}{2})^2;\)muhimu inakuwa\(\displaystyle −∫^{5/4}_{5/4}\frac{1}{u}\,du\).

57)\(\displaystyle ∫^π_0\sin\left(\left(t−\tfrac{π}{2}\right)^3\right)\cos\left(t−\tfrac{π}{2}\right)\,dt\)

58)\(\displaystyle ∫^2_0(1−t)\cos(πt)\,dt\)

Jibu

\(u=1−t;\)Tangu integrand ni isiyo ya kawaida, muhimu inakuwa
\[∫^{−1}_1u\cos\big(π(1−u)\big)\,du=∫^{−1}_1u[\cos π\cos u−\sin π\sin u]\,du=−∫^{−1}_1u\cos u\,du=∫_{-1}^1u\cos u\,du=0\nonumber \]

59)\(\displaystyle ∫^{3π/4}_{π/4}\sin^2 t\cos t\,dt\)

60) Onyesha kwamba thamani ya wastani ya\(f(x)\) zaidi ya muda\([a,b]\) ni sawa na thamani ya wastani ya\(f(cx)\) zaidi ya\(\left[\frac{a}{c},\frac{b}{c}\right]\) muda\(c>0.\)

Jibu

Kuweka\(u=cx\) na\(du=c\,dx\) anapata wewe\(\displaystyle \frac{1}{\frac{b}{c}−\frac{a}{c}}∫^{b/c}_{a/c}f(cx)\,dx=\frac{c}{b−a}∫^{u=b}_{u=a}f(u)\frac{du}{c}=\frac{1}{b−a}∫^b_af(u)\,du.\)

61) Kupata eneo chini ya grafu ya\(f(t)=\dfrac{t}{(1+t^2)^a}\) kati\(t=0\) na\(t=x\) wapi\(a>0\) na\(a≠1\) ni fasta, na kutathmini kikomo kama\(x→∞\).

62) Pata eneo chini ya grafu ya\(g(t)=\dfrac{t}{(1−t^2)^a}\) kati\(t=0\) na\(t=x\), wapi\(0<x<1\) na\(a>0\) ni fasta. Kutathmini kikomo kama\(x→1\).

Jibu

\(\displaystyle ∫^x_0g(t)\,dt=\frac{1}{2}∫^1_{u=1−x^2} \frac{du}{u^a}=\frac{1}{2(1−a)}u^{1−a}∣1u=\frac{1}{2(1−a)}(1−(1−x^2)^{1−a})\)Kama\(x→1\) kikomo ni\(\dfrac{1}{2(1−a)}\) kama\(a<1\), na kikomo diverges na\(+∞\) kama\(a>1\).

63) Eneo la semicircle ya radius\(1\) linaweza kuelezwa kama\(\displaystyle ∫^1_{−1}\sqrt{1−x^2}\,dx\). Tumia badala ya\(x=\cos t\) kuelezea eneo la semicircle kama muhimu ya kazi ya trigonometric. Huna haja ya kukokotoa muhimu.

64) Eneo la nusutufe ya juu ya duaradufu lenye mhimili mkubwa\(x\) yaani -mhimili kutoka\(x=−1\) kwa a na lenye mhimili mdogo yaani\(y\) -mhimili kutoka\(y=−b\) kwa\(y=b\) inaweza kuandikwa kama\(\displaystyle ∫^a_{−a}b\sqrt{1−\frac{x^2}{a^2}}\,dx\). Tumia nafasi ya\(x=a\cos t\) kuelezea eneo hili kwa suala la muhimu ya kazi ya trigonometric. Huna haja ya kukokotoa muhimu.

Jibu

\(\displaystyle ∫^{t=0}_{t=π}b\sqrt{1−\cos^2 t}×(−a\sin t)\,dt=∫^{t=π}_{t=0}ab\sin^2 t\,dt\)

65) [T] Grafu ifuatayo ni ya kazi ya fomu\( f(t)=a\sin(nt)+b\sin(mt)\). Tathmini coefficients\(a\)\(b\) na vigezo vya mzunguko\(n\) na\(m\). Tumia makadirio haya kwa takriban\(\displaystyle ∫^π_0f(t)\,dt\).

66) [T] Grafu ifuatayo ni ya kazi ya fomu\(f(x)=a\cos(nt)+b\cos(mt)\). Tathmini coefficients\(a\)\(b\) na vigezo vya mzunguko\(n\) na\(m\). Tumia makadirio haya kwa takriban\(\displaystyle ∫^π_0f(t)\,dt.\)

Jibu

\(f(t)=2\cos(3t)−\cos(2t);\quad \displaystyle ∫^{π/2}_0(2\cos(3t)−\cos(2t))\,dt=−\frac{2}{3}\)