4.10: Antiderivatives

Malengo ya kujifunza

• Pata antiderivative ya jumla ya kazi iliyotolewa.
• Eleza maneno na nukuu kutumika kwa ajili ya muhimu kwa muda usiojulikana.
• Hali ya utawala wa nguvu kwa integrals.
• Tumia antipambatification kutatua matatizo rahisi ya awali ya thamani.

Kwa hatua hii, tumeona jinsi ya kuhesabu derivatives ya kazi nyingi na imeanzishwa kwa aina mbalimbali za maombi yao. Sisi sasa kuuliza swali kwamba anarudi mchakato huu karibu: Kutokana na kazi\(f\), jinsi gani sisi kupata kazi na derivative\(f\) na kwa nini sisi kuwa na nia ya kazi hiyo?

Tunajibu sehemu ya kwanza ya swali hili kwa kufafanua antiderivatives. Antiderivative ya kazi\(f\) ni kazi na derivative\(f\). Kwa nini tunavutiwa na antiderivatives? Mahitaji ya antiderivatives hutokea katika hali nyingi, na tunaangalia mifano mbalimbali katika salio la maandishi. Hapa tunachunguza mfano mmoja maalum ambao unahusisha mwendo wa kawaida. Katika uchunguzi wetu katika Derivatives ya mwendo rectilinear, sisi ilionyesha kuwa kutokana na nafasi\(s(t)\) ya kazi ya kitu, basi kasi yake kazi\(v(t)\) ni derivative ya\(s(t)\) - yaani,\(v(t)=s′(t)\). Zaidi ya hayo, kuongeza kasi\(a(t)\) ni derivative ya kasi\(v(t)\) - yaani,\(a(t)=v′(t)=s''(t)\). Sasa tuseme tunapewa kazi ya kuongeza kasi\(a\), lakini si kazi ya kasi\(v\) au kazi ya msimamo\(s\). Kwa kuwa\(a(t)=v′(t)\), kuamua kazi ya kasi inahitaji sisi kupata antiderivative ya kazi ya kuongeza kasi. Kisha, tangu\(v(t)=s′(t),\) kuamua kazi ya msimamo inahitaji sisi kupata antiderivative ya kazi ya kasi. Mwendo wa kawaida ni kesi moja tu ambayo haja ya antiderivatives hutokea. Tutaona mifano mingi zaidi katika salio la maandishi. Kwa sasa, hebu tuangalie nenosiri na uthibitisho wa antiderivatives, na ueleze antiderivatives kwa aina kadhaa za kazi. Tunachunguza mbinu mbalimbali za kutafuta antiderivatives ya kazi ngumu zaidi baadaye katika maandiko (Utangulizi wa Mbinu za Ushirikiano).

Reverse ya Tofauti

Kwa hatua hii, tunajua jinsi ya kupata derivatives ya kazi mbalimbali. Sasa tunauliza swali kinyume. Kutokana na kazi\(f\), tunawezaje kupata kazi na derivative\(f\)? Kama tunaweza kupata kazi\(F\) na derivative\(f,\) tunaita\(F\) antiderivative ya\(f\).

Ufafanuzi: Antiderative

kazi\(F\) ni antiderivative ya kazi\(f\) kama

\[F′(x)=f(x) \nonumber \]

kwa wote\(x\) katika uwanja wa\(f\).

Fikiria kazi\(f(x)=2x\). Kujua utawala wa nguvu wa kutofautisha, tunahitimisha kuwa\(F(x)=x^2\) ni antiderivative ya\(f\) tangu\(F′(x)=2x\).

Je, kuna antiderivatives nyingine yoyote ya\(f\)?

Ndiyo; tangu derivative ya mara kwa mara yoyote\(C\) ni sifuri, pia\(x^2+C\) ni antiderivative ya\(2x\). Kwa hiyo,\(x^2+5\) na pia\(x^2−\sqrt{2}\) ni antiderivatives.

Je, kuna wengine ambao si wa fomu\(x^2+C\) kwa baadhi ya mara kwa mara\(C\)?

Jibu ni hapana. Kutoka Corollary 2 ya Theorem Mean Thamani, tunajua kwamba kama\(F\) na\(G\) ni tofauti kazi kama kwamba\(F′(x)=G′(x),\) basi\(F(x)−G(x)=C\) kwa baadhi ya mara kwa mara\(C\). Ukweli huu unasababisha theorem muhimu yafuatayo.

Theorem\(\PageIndex{1}\): General Form of an Antiderivative

Hebu\(F\) kuwa antiderivative ya\(f\) zaidi ya muda\(I\). Kisha,

1. kwa kila mara\(C\), kazi pia\(F(x)+C\) ni antiderivative ya\(f\) juu\(I\);
2. kama\(G\) ni antiderivative ya\(f\) juu\(I\), kuna mara kwa mara kwa\(C\) ajili ya ambayo\(G(x)=F(x)+C\) juu ya\(I\).

Kwa maneno mengine, fomu ya jumla ya antiderivative ya\(f\) juu\(I\) ni\(F(x)+C\).

Tunatumia ukweli huu na ujuzi wetu wa derivatives ili kupata antiderivatives zote kwa kazi kadhaa.

Mfano\(\PageIndex{1}\): Finding Antiderivatives

Kwa kila moja ya kazi zifuatazo, pata antiderivatives zote.

1. \(f(x)=3x^2\)
2. \(f(x)=\dfrac{1}{x}\)
3. \(f(x)=\cos x\)
4. \(f(x)=e^x\)

Suluhisho:

a. kwa sababu

\[\dfrac{d}{dx}\left(x^3\right)=3x^2 \nonumber \]

basi\(F(x)=x^3\) ni antiderivative ya\(3x^2\). Kwa hiyo, kila antiderivative ya\(3x^2\) ni ya fomu\(x^3+C\) kwa baadhi ya mara kwa mara\(C\), na kila kazi ya fomu\(x^3+C\) ni antiderivative ya\(3x^2\).

b Hebu\(f(x)=\ln |x|.\)

Kwa\(x>0,\; f(x)=\ln |x|=\ln (x)\) na

\[\dfrac{d}{dx}\Big(\ln x\Big)=\dfrac{1}{x}. \nonumber \]

Kwa\(x<0,\; f(x)=\ln |x|=\ln (−x)\) na

\[\dfrac{d}{dx}\Big(\ln (−x)\Big)=−\dfrac{1}{−x}=\dfrac{1}{x}. \nonumber \]

Kwa hiyo,

\[\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}. \nonumber \]

Hivyo,\(F(x)=\ln |x|\) ni antiderivative ya\(\dfrac{1}{x}\). Kwa hiyo, kila antiderivative ya\(\dfrac{1}{x}\) ni ya fomu\(\ln |x|+C\) kwa baadhi ya mara kwa mara\(C\) na kila kazi ya fomu\(\ln |x|+C\) ni antiderivative ya\(\dfrac{1}{x}\).

c. tuna

\[\dfrac{d}{dx}\Big(\sin x\Big)=\cos x, \nonumber \]

hivyo\(F(x)=\sin x\) ni antiderivative ya\(\cos x\). Kwa hiyo, kila antiderivative ya\(\cos x\) ni ya fomu\(\sin x+C\) kwa baadhi ya mara kwa mara\(C\) na kila kazi ya fomu\(\sin x+C\) ni antiderivative ya\(\cos x\).

d Tangu

\[\dfrac{d}{dx}\left(e^x\right)=e^x, \nonumber \]

basi\(F(x)=e^x\) ni antiderivative ya\(e^x\). Kwa hiyo, kila antiderivative ya\(e^x\) ni ya fomu\(e^x+C\) kwa baadhi ya mara kwa mara\(C\) na kila kazi ya fomu\(e^x+C\) ni antiderivative ya\(e^x\).

Zoezi\(\PageIndex{1}\)

Kupata antiderivatives wote wa\(f(x)=\sin x\).

Kidokezo

Ni kazi gani ina derivative ya\(\sin x\)?

Jibu

\(F(x) = −\cos x+C\)

Integrals muda usiojulikana

Sasa tunaangalia nukuu rasmi iliyotumiwa kuwakilisha antiderivatives na kuchunguza baadhi ya mali zao. Mali hizi zinatuwezesha kupata antiderivatives ya kazi ngumu zaidi. Kutokana na kazi\(f\), sisi kutumia nukuu\(f′(x)\) au\(\dfrac{df}{dx}\) kuashiria derivative ya\(f\). Hapa tunaanzisha notation kwa antiderivatives. Kama\(F\) ni antiderivative ya\(f\), tunasema kwamba\(F(x)+C\) ni antiderivative ya jumla ya\(f\) na kuandika

\[\int f(x)\,dx=F(x)+C.\nonumber \]

Ishara\(\displaystyle \int \) inaitwa ishara muhimu, na\(\displaystyle \int f(x)\,dx\) inaitwa muhimu ya muda usiojulikana ya\(f\).

Ufafanuzi: Integrals isiyojulikana

Kutokana na kazi\(f\), muhimu kwa muda usiojulikana\(f\), ulionyehsa

\[\int f(x)\,dx, \nonumber \]

ni antiderivative ya jumla ya\(f\). Kama\(F\) ni antiderivative ya\(f\), basi

\[\int f(x)\,dx=F(x)+C. \nonumber \]

Maneno\(f(x)\) huitwa integrand na variable\(x\) ni variable ya ushirikiano.

Kutokana na istilahi iliyoanzishwa katika ufafanuzi huu, kitendo cha kutafuta antiderivatives ya kazi\(f\) kwa kawaida hujulikana kama kuunganisha\(f\).

Kwa kazi\(f\) na antiderivative\(F\), kazi\(F(x)+C\), ambapo\(C\) ni idadi yoyote halisi, mara nyingi hujulikana kama familia ya antiderivatives ya\(f\). Kwa mfano, tangu\(x^2\) ni antiderivative ya\(2x\) na antiderivative yoyote ya\(2x\) ni ya fomu\(x^2+C,\) tunayoandika

\[\int 2x\,dx=x^2+C.\nonumber \]

Mkusanyiko wa kazi zote za fomu\(x^2+C,\) ambapo\(C\) ni idadi yoyote halisi, inajulikana kama familia ya antiderivatives ya\(2x\). Kielelezo\(\PageIndex{1}\) kinaonyesha grafu ya familia hii ya antiderivatives.

Kielelezo\(\PageIndex{1}\): Familia ya antiderivatives\(2x\) ina kazi zote za fomu\(x^2+C\),\(C\) wapi idadi yoyote halisi.

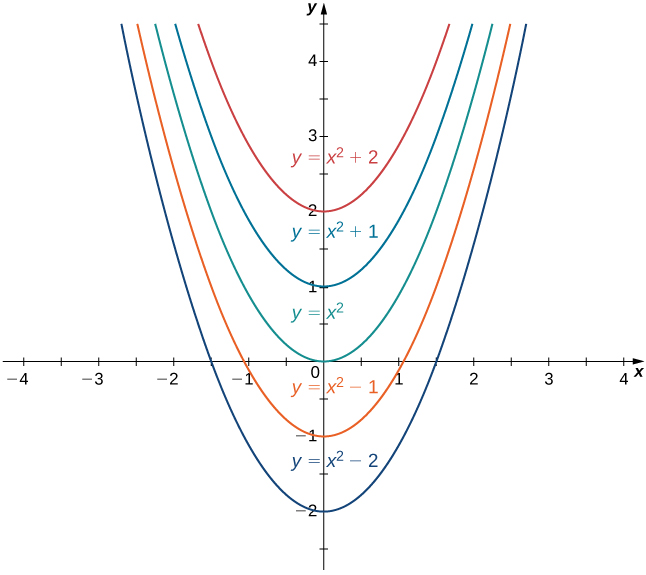
Kwa kazi fulani, kutathmini integrals isiyojulikana ifuatavyo moja kwa moja kutoka kwa mali ya derivatives. Kwa mfano, kwa\(n≠−1\),

\(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C,\)

ambayo huja moja kwa moja kutoka

\(\dfrac{d}{dx}\left(\dfrac{x^{n+1}}{n+1}\right)=(n+1)\dfrac{x^n}{n+1}=x^n\).

Ukweli huu unajulikana kama utawala wa nguvu kwa integrals.

Utawala wa Power kwa Integrals

Kwa\(n≠−1,\)

\[\int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C. \nonumber \]

Kutathmini integrals kwa muda usiojulikana kwa baadhi ya kazi nyingine pia ni hesabu moja kwa moja. Jedwali lifuatayo linaorodhesha integrals isiyojulikana kwa kazi kadhaa za kawaida. Orodha kamili zaidi inaonekana katika Kiambatisho B.

Jedwali\(\PageIndex{1}\): Fomu za Ushir

Tofauti formula	Muda usiojulikana muhimu
\(\dfrac{d}{dx}\Big(k\Big)=0\)	\(\displaystyle \int k\,dx=\int kx^0\,dx=kx+C\)
\(\dfrac{d}{dx}\Big(x^n\Big)=nx^{n−1}\)	\(\displaystyle \int x^n\,dx=\dfrac{x^{n+1}}{n+1}+C\)kwa\(n≠−1\)
\(\dfrac{d}{dx}\Big(\ln |x|\Big)=\dfrac{1}{x}\)	\(\displaystyle \int \dfrac{1}{x}\,dx=\ln |x|+C\)
\(\dfrac{d}{dx}\Big(e^x\Big)=e^x\)	\(\displaystyle \int e^x\,dx=e^x+C\)
\(\dfrac{d}{dx}\Big(\sin x\Big)=\cos x\)	\(\displaystyle \int \cos x\,dx=\sin x+C\)
\(\dfrac{d}{dx}\Big(\cos x\Big)=−\sin x\)	\(\displaystyle \int \sin x\,dx=−\cos x+C\)
\(\dfrac{d}{dx}\Big(\tan x\Big)=\sec^2 x\)	\(\displaystyle \int \sec^2 x\,dx=\tan x+C\)
\(\dfrac{d}{dx}\Big(\csc x\Big)=−\csc x\cot x\)	\(\displaystyle \int \csc x\cot x\,dx=−\csc x+C\)
\(\dfrac{d}{dx}\Big(\sec x\Big)=\sec x\tan x\)	\(\displaystyle \int \sec x\tan x\,dx=\sec x+C\)
\(\dfrac{d}{dx}\Big(\cot x\Big)=−\csc^2 x\)	\(\displaystyle \int \csc^2x\,dx=−\cot x+C\)
\(\dfrac{d}{dx}\Big(\sin^{−1}x\Big)=\dfrac{1}{\sqrt{1−x^2}}\)	\(\displaystyle \int \dfrac{1}{\sqrt{1−x^2}}=\sin^{−1}x+C\)
\(\dfrac{d}{dx}\Big(\tan^{−1}x\Big)=\dfrac{1}{1+x^2}\)	\(\displaystyle \int \dfrac{1}{1+x^2}\,dx=\tan^{−1}x+C\)
\(\dfrac{d}{dx}\Big(\sec^{−1}|x|\Big)=\dfrac{1}{x\sqrt{x^2−1}}\)	\(\displaystyle \int \dfrac{1}{x\sqrt{x^2−1}}\,dx=\sec^{−1}|x|+C\)

Kutokana na ufafanuzi wa muhimu kwa muda usiojulikana\(f\), tunajua

\[\int f(x)\,dx=F(x)+C\nonumber \]

kama na tu kama\(F\) ni antiderivative ya\(f\).

Kwa hiyo, wakati wa kudai kwamba

\[\int f(x)\,dx=F(x)+C\nonumber \]

ni muhimu kuangalia kama kauli hii ni sahihi kwa kuthibitisha kwamba\(F′(x)=f(x).\)

Mfano\(\PageIndex{2}\): Verifying an Indefinite Integral

Kila moja ya kauli zifuatazo ni ya fomu\(\displaystyle \int f(x)\,dx=F(x)+C.\) Thibitisha kwamba kila taarifa ni sahihi kwa kuonyesha kwamba\(F′(x)=f(x).\)

1. \(\displaystyle\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C\)
2. \(\displaystyle\int xe^x\,dx=xe^x−e^x+C\)

Suluhisho:

a. tangu

\(\dfrac{d}{dx}\left(\dfrac{x^2}{2}+e^x+C\right)=x+e^x\),

taarifa

\[\int \big(x+e^x\big)\,dx=\dfrac{x^2}{2}+e^x+C \nonumber \]

ni sahihi.

Kumbuka kwamba sisi ni kuthibitisha muhimu kwa muda usiojulikana kwa jumla. Zaidi ya hayo,\(\dfrac{x^2}{2}\) na\(e^x\) ni antiderivatives ya\(x\) na\(e^x\), kwa mtiririko huo, na jumla ya antiderivatives ni antiderivative ya jumla. Tunajadili ukweli huu tena baadaye katika sehemu hii.

b Kutumia utawala wa bidhaa, tunaona hiyo

\[\dfrac{d}{dx}\left(xe^x−e^x+C\right)=e^x+xe^x−e^x=xe^x. \nonumber \]

Kwa hiyo, taarifa

\[\int xe^x\,dx=xe^x−e^x+C \nonumber \]

ni sahihi.

Kumbuka kwamba sisi ni kuthibitisha muhimu kwa muda usiojulikana kwa bidhaa. Antiderivative\(xe^x−e^x\) sio bidhaa ya antiderivatives. Zaidi ya hayo, bidhaa ya antiderivatives,\(x^2e^x/2\) si antiderivative ya\(xe^x\) tangu

\(\dfrac{d}{dx}\left(\dfrac{x^2e^x}{2}\right)=xe^x+\dfrac{x^2e^x}{2}≠xe^x\).

Kwa ujumla, bidhaa za antiderivatives sio antiderivative ya bidhaa.

Zoezi\(\PageIndex{2}\)

Thibitisha kwamba\(\displaystyle \int x\cos x\,\,dx=x\sin x+\cos x+C.\)

Kidokezo

Tumia\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big).\)

Jibu

\(\dfrac{d}{dx}\Big(x\sin x+\cos x+C\Big)=\sin x+x\cos x−\sin x=x \cos x\)

Katika Jedwali\(\PageIndex{1}\), tuliorodhesha integrals isiyojulikana kwa kazi nyingi za msingi. Hebu sasa tugeuke mawazo yetu kwa kutathmini integrals isiyojulikana kwa kazi ngumu zaidi. Kwa mfano, fikiria kutafuta antiderivative ya jumla\(f+g\). Katika Mfano\(\PageIndex{2}a\) tulionyesha kuwa antiderivative ya jumla\(x+e^x\) hutolewa kwa jumla\(\dfrac{x^2}{2}+e^x\) - yaani, antiderivative ya jumla hutolewa kwa jumla ya antiderivatives. Matokeo haya hayakuwa maalum kwa mfano huu. Kwa ujumla, ikiwa\(F\) na\(G\) ni antiderivatives ya kazi yoyote\(f\) na\(g\), kwa mtiririko huo, basi

\(\dfrac{d}{dx}\big(F(x)+G(x)\big)=F′(x)+G′(x)=f(x)+g(x).\)

Kwa hiyo,\(F(x)+G(x)\) ni antiderivative ya\(f(x)+g(x)\) na tuna

\[ \int \big(f(x)+g(x)\big)\,dx=F(x)+G(x)+C.\nonumber \]

Vile vile,

\[ \int \big(f(x)−g(x)\big)\,dx=F(x)−G(x)+C.\nonumber \]

Kwa kuongeza, fikiria kazi ya kutafuta antiderivative ya\(kf(x),\)\(k\) wapi idadi yoyote halisi. Tangu

\[ \dfrac{d}{dx}\Big(kF(x)\Big)=k\dfrac{d}{dx}\Big(F(x)\Big)=kF′(x)\nonumber \]

kwa idadi yoyote halisi\(k\), tunahitimisha kuwa

\[ \int kf(x)\,dx=kF(x)+C.\nonumber \]

Mali hizi ni muhtasari ijayo.

Mali ya Integrals isiyojulikana

Hebu\(F\) na\(G\) uwe na antiderivatives ya\(f\) na\(g\), kwa mtiririko huo, na\(k\) uwe na idadi yoyote halisi.

Jumla na Tofauti

\[\int \big(f(x)±g(x)\big)\,dx=F(x)±G(x)+C \nonumber \]

Mara kwa mara nyingi

\[ \int kf(x)\,dx=kF(x)+C \nonumber \]

Kutoka theorem hii, tunaweza kutathmini muhimu yoyote inayohusisha jumla, tofauti, au mara kwa mara nyingi ya kazi na antiderivatives ambazo zinajulikana. Kutathmini integrals kuwashirikisha bidhaa, quotients, au nyimbo ni ngumu zaidi. (Angalia Mfano\(\PageIndex{2}b\) kwa mfano kuwashirikisha antiderivative ya bidhaa.) Tunaangalia na kushughulikia integrals kuwashirikisha kazi hizi ngumu zaidi katika Utangulizi wa Ushirikiano. Katika mfano unaofuata, tunachunguza jinsi ya kutumia theorem hii kuhesabu integrals isiyojulikana ya kazi kadhaa.

Mfano\(\PageIndex{3}\): Evaluating Indefinite Integrals

Kutathmini kila moja ya integrals yafuatayo kwa muda usiojulikana:

1. \(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx\)
2. \(\displaystyle \int \dfrac{x^2+4\sqrt[3]{x}}{x}\,dx\)
3. \(\displaystyle \int \dfrac{4}{1+x^2}\,dx\)
4. \(\displaystyle \int \tan x\cos x\,dx\)

Suluhisho:

a Kutumia Mali ya Integrals isiyojulikana, tunaweza kuunganisha kila moja ya masharti manne katika integrand tofauti. Tunapata

\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx.\)

Kutoka sehemu ya pili ya Mali ya Integrals isiyojulikana, kila mgawo unaweza kuandikwa mbele ya ishara muhimu, ambayo inatoa

\(\displaystyle \int 5x^3\,dx−\int 7x^2\,dx+\int 3x\,dx+\int 4\,dx=5\int x^3\,dx−7\int x^2\,dx+3\int x\,dx+4\int 1\,dx.\)

Kutumia utawala wa nguvu kwa integrals, tunahitimisha kuwa

\(\displaystyle \int \big(5x^3−7x^2+3x+4\big)\,dx=\dfrac{5}{4}x^4−\dfrac{7}{3}x^3+\dfrac{3}{2}x^2+4x+C.\)

b Andika upya integrand kama

\(\dfrac{x^2+4\sqrt[3]{x}}{x}=\dfrac{x^2}{x}+\dfrac{4\sqrt[3]{x}}{x}.\)

Kisha, ili kutathmini muhimu, kuunganisha kila moja ya masharti haya tofauti. Kutumia utawala wa nguvu, tuna

\ [kuanza {align*}\ int\ kushoto (x+\ dfrac {4} {x^ {2/3}}\ haki)\, dx&=\ int x\, dx+4\ int x^ {-2/3}\, dx\\ [4pt]
&=\ dfrac {1} {1} {2} x ^ 2+4\ dfrac {1} {1} {tfrac {ї2} {3}\ haki) +1} x^ {(-2/3) +1} +C\\ [4pt]
&=\ dfrac {1} {2} x ^ 2+12x^ {1/3} +C.\ mwisho {align*}\]

c Kutumia Mali ya Integrals kwa muda usiojulikana, kuandika muhimu kama

\(4\displaystyle \int \dfrac{1}{1+x^2}\,dx.\)

Kisha, kutumia ukweli kwamba\(\tan^{−1}(x)\) ni antiderivative ya\(\dfrac{1}{1+x^2}\) kuhitimisha kwamba

\(\displaystyle \int \dfrac{4}{1+x^2}\,dx=4\tan^{−1}(x)+C.\)

d. rewrite integrand kama

\(\tan x\cos x=\dfrac{\sin x}{\cos x}\cdot\cos x=\sin x.\)

Kwa hiyo,

\(\displaystyle \int \tan x\cos x\,dx=\int \sin x\,dx=−\cos x+C.\)

Zoezi\(\PageIndex{3}\)

Tathmini\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx\).

Kidokezo

Unganisha kila neno katika integrand tofauti, ukitumia utawala wa nguvu.

Jibu

\(\displaystyle \int \big(4x^3−5x^2+x−7\big)\,dx = \quad x^4−\dfrac{5}{3}x^3+\dfrac{1}{2}x^2−7x+C\)

Matatizo ya Thamani ya awali

Tunaangalia mbinu za kuunganisha kazi mbalimbali zinazohusisha bidhaa, quotients, na nyimbo baadaye katika maandiko. Hapa tunageuka kwenye matumizi moja ya kawaida kwa antiderivatives ambayo hutokea mara nyingi katika maombi mengi: kutatua equations tofauti.

Equation tofauti ni equation inayohusiana na kazi isiyojulikana na moja au zaidi ya derivatives yake. equation

\[\dfrac{dy}{dx}=f(x)\label{diffeq1} \]

ni mfano rahisi wa equation tofauti. Kutatua equation hii inamaanisha kutafuta kazi\(y\) na derivative\(f\). Kwa hiyo, ufumbuzi wa Equation\ ref {differeq1} ni antiderivatives ya\(f\). Kama\(F\) ni antiderivative moja ya\( f\), kila kazi ya fomu\( y=F(x)+C\) ni suluhisho la equation kwamba tofauti. Kwa mfano, ufumbuzi wa

\[\dfrac{dy}{dx}=6x^2\nonumber \]

hutolewa na

\[y=\int 6x^2\,dx=2x^3+C.\nonumber \]

Wakati mwingine sisi ni nia ya kuamua kama fulani ufumbuzi Curve hupita kwa njia fulani\( (x_0,y_0)\) - yaani,\( y(x_0)=y_0\). Tatizo la kutafuta kazi\(y\) ambayo inatimiza equation tofauti

\(\dfrac{dy}{dx}=f(x)\)

na hali ya ziada

\(y(x_0)=y_0\)

ni mfano wa tatizo la thamani ya awali. Hali\( y(x_0)=y_0\) inajulikana kama hali ya awali. Kwa mfano, kutafuta kazi\( y\) ambayo satisfies equation tofauti

\(\dfrac{dy}{dx}=6x^2\)

na hali ya awali

\(y(1)=5\)

ni mfano wa tatizo la thamani ya awali. Kwa kuwa ufumbuzi wa equation tofauti ni\( y=2x^3+C,\) kupata kazi\(y\) ambayo pia inatimiza hali ya awali, tunahitaji kupata\(C\) hiyo\(y(1)=2(1)^3+C=5\). Kutoka equation hii, tunaona kwamba\( C=3\), na sisi kuhitimisha kwamba\( y=2x^3+3\) ni ufumbuzi wa tatizo hili awali thamani kama inavyoonekana katika graph zifuatazo.

Kielelezo\(\PageIndex{2}\): Baadhi ya curves ufumbuzi wa equation tofauti\(\dfrac{dy}{dx}=6x^2\) ni kuonyeshwa. Kazi\(y=2x^3+3\) hutimiza equation tofauti na hali ya awali\(y(1)=5.\)

Mfano\(\PageIndex{4}\): Solving an Initial-Value Problem

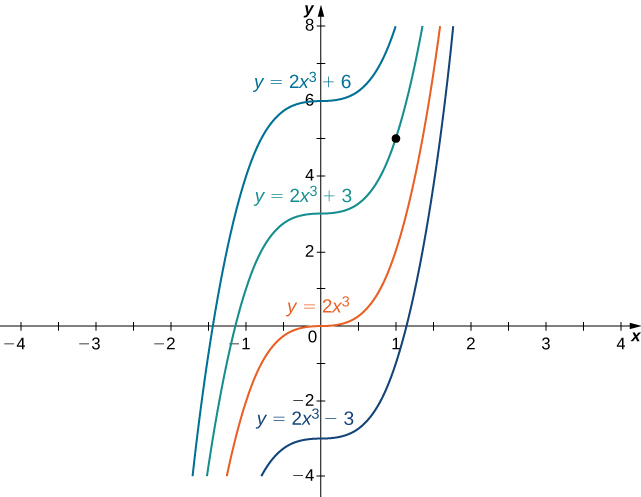
Tatua tatizo la thamani ya awali

\[\dfrac{dy}{dx}=\sin x,\quad y(0)=5.\nonumber \]

Suluhisho

Kwanza tunahitaji kutatua equation tofauti. Ikiwa\(\dfrac{dy}{dx}=\sin x\), basi

\[y=\displaystyle \int \sin(x)\,dx=−\cos x+C.\nonumber \]

Halafu tunahitaji kutafuta suluhisho\(y\) ambalo linatimiza hali ya awali. Hali ya awali\(y(0)=5\) ina maana tunahitaji mara kwa mara\(C\) vile kwamba\(−\cos x+C=5.\) Kwa hiyo,

\[C=5+\cos(0)=6.\nonumber \]

Suluhisho la tatizo la thamani ya awali ni\(y=−\cos x+6.\)

Zoezi\(\PageIndex{4}\)

Tatua tatizo la thamani ya awali\(\dfrac{dy}{dx}=3x^{−2},\quad y(1)=2\).

Kidokezo

Find antiderivatives wote wa\(f(x)=3x^{−2.}\)

Jibu

\(y=−\dfrac{3}{x}+5\)

Matatizo ya thamani ya awali hutokea katika programu nyingi. Halafu tunazingatia tatizo ambalo dereva hutumia breki katika gari. Tunavutiwa na muda gani inachukua gari kuacha. Kumbuka kwamba kazi ya kasi\(v(t)\) ni derivative ya kazi ya msimamo\(s(t),\) na kuongeza kasi\(a(t)\) ni derivative ya kazi ya kasi. Katika mifano ya awali katika maandishi, tunaweza kuhesabu kasi kutoka nafasi na kisha kukokotoa kuongeza kasi kutoka kasi. Katika mfano unaofuata tunafanya kazi kwa njia nyingine kote. Kutokana na kazi ya kuongeza kasi, tunahesabu kazi ya kasi. Tunatumia kazi ya kasi ili kuamua kazi ya msimamo.

Mfano\(\PageIndex{5}\):

Gari linasafiri kwa kiwango cha\(88\) ft/sec (\(60\)mph) wakati breki zinatumika. Gari huanza kupungua kwa kiwango cha mara kwa mara cha\(15\) ft/sec ².

1. Ni sekunde ngapi zinazopita kabla ya gari kuacha?
2. Je! Gari linasafiri mbali gani wakati huo?

Suluhisho

a. kwanza sisi kuanzisha vigezo kwa tatizo hili. Hebu\(t\) kuwa wakati (kwa sekunde) baada ya breki kutumika kwanza. Hebu\(a(t)\) kuwa kasi ya gari (kwa miguu kwa sekunde squared) kwa wakati\(t\). Hebu\(v(t)\) iwe kasi ya gari (kwa miguu kwa pili) kwa wakati\(t\). Hebu\(s(t)\) kuwa msimamo wa gari (kwa miguu) zaidi ya hatua ambapo breki hutumiwa wakati\(t\).

Gari linasafiri kwa kiwango cha\(88\) ft/sec. Kwa hiyo, kasi ya awali ni\(v(0)=88\) ft/sec. Tangu gari ni decelerating, kuongeza kasi ni

\(a(t)=−15\,\text{ft/sec}^2\).

Kuongeza kasi ni derivative ya kasi,

\(v′(t)=-15.\)

Kwa hiyo, tuna tatizo la thamani ya awali ya kutatua:

\(v′(t)=−15,\quad v(0)=88.\)

Kuunganisha, tunaona kwamba

\(v(t)=−15t+C.\)

Tangu\(v(0)=88,C=88.\) Hivyo, kazi kasi ni

\(v(t)=−15t+88.\)

Ili kupata muda gani inachukua gari kuacha, tunahitaji kupata muda\(t\) kama vile kasi ni sifuri. Kutatua\(−15t+88=0,\) sisi kupata\(t=\dfrac{88}{15}\) sec.

b Ili kujua jinsi gari linasafiri wakati huu, tunahitaji kupata nafasi ya gari baada ya\(\dfrac{88}{15}\) sec. Tunajua kasi\(v(t)\) ni derivative ya nafasi\(s(t)\). Fikiria nafasi ya kwanza kuwa\(s(0)=0\). Kwa hiyo, tunahitaji kutatua tatizo la thamani ya awali

\(s′(t)=−15t+88,\quad s(0)=0.\)

Kuunganisha, tuna

\(s(t)=−\dfrac{15}{2}t^2+88t+C.\)

Tangu\(s(0)=0\), mara kwa mara ni\(C=0\). Kwa hiyo, kazi ya msimamo ni

\(s(t)=−\dfrac{15}{2}t^2+88t.\)

Baada ya\(t=\frac{88}{15}\) sekunde, nafasi ni\(s\left(\frac{88}{15}\right)≈258.133\) ft.

Zoezi\(\PageIndex{5}\)

Tuseme gari linasafiri kwa kiwango cha\(44\) ft/sec. Inachukua muda gani kwa gari kuacha? Je! Gari litaondoka mbali gani?

Kidokezo

\(v(t)=−15t+44.\)

Jibu

\(2.93\)sekunde,\(64.5\) ft

Dhana muhimu

• Ikiwa\(F\) ni antiderivative ya\(f,\) basi kila antiderivative ya\(f\) ni ya fomu\(F(x)+C\) kwa baadhi ya mara kwa mara\(C\).
• Kutatua tatizo la thamani ya awali\[\dfrac{dy}{dx}=f(x),\quad y(x_0)=y_0 \nonumber \] inahitaji sisi kwanza kupata seti ya antiderivatives ya\(f\) na kisha kutafuta antiderivative fulani ambayo pia inatimiza hali ya awali.

faharasa

antiderivative

kazi\(F\) kama kwamba\(F′(x)=f(x)\) kwa ajili ya wote\(x\) katika uwanja wa\(f\) ni antiderivative ya\(f\)

muda usiojulikana muhimu

antiderivative ya jumla ya\(f(x)\) ni muhimu kwa muda usiojulikana ya\(f\); tunatumia nukuu\(\displaystyle \int f(x)\,dx\) kuashiria muhimu ya muda usiojulikana\(f\)

tatizo la thamani ya awali

tatizo ambalo linahitaji kutafuta kazi\(y\) ambayo inatimiza usawa tofauti\(\dfrac{dy}{dx}=f(x)\) pamoja na hali ya awali\(y(x_0)=y_0\)