4.9: Njia ya Newton

Last updated
Save as PDF

Page ID: 178855

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Eleza hatua za njia ya Newton.
Eleza nini mchakato wa iterative unamaanisha.
Tambua wakati njia ya Newton haifanyi kazi.
Tumia michakato ya iterative kwa hali mbalimbali.

Katika maeneo mengi ya hisabati safi na kutumika, sisi ni nia ya kutafuta ufumbuzi wa equation ya fomu\(f(x)=0.\) Kwa kazi nyingi, hata hivyo, ni vigumu-kama siwezekani-kuhesabu zero zao wazi. Katika sehemu hii, tunaangalia mbinu ambayo hutoa njia nzuri sana ya kukadiria zero za kazi. Mbinu hii inafanya matumizi ya makadirio tangent line na ni nyuma ya njia inayotumiwa mara nyingi na calculators na kompyuta ya kupata zeroes.

Akielezea Method ya Newton

Fikiria kazi ya kutafuta ufumbuzi wa\(f(x)=0.\) Kama\(f\) ni polynomial ya shahada ya kwanza\(f(x)=ax+b\), basi suluhisho la\(f(x)=0\) hutolewa na formula\(x=−\frac{b}{a}\). Ikiwa\(f\) ni polynomial ya shahada ya pili\(f(x)=ax^2+bx+c\), ufumbuzi wa\(f(x)=0\) unaweza kupatikana kwa kutumia formula ya quadratic. Hata hivyo, kwa polynomials ya shahada 3 au zaidi, kutafuta mizizi ya\(f\) inakuwa ngumu zaidi. Ingawa formula zipo kwa polynomials ya tatu na ya nne, ni ngumu sana. Pia, ikiwa f ni polynomial ya shahada ya 5 au zaidi, inajulikana kuwa hakuna kanuni hizo zilizopo. Kwa mfano, fikiria kazi

\[f(x)=x^5+8x^4+4x^3−2x−7.\nonumber \]

Hakuna formula iliyopo ambayo inaruhusu sisi kupata ufumbuzi wa matatizo\(f(x)=0.\) sawa zipo kwa kazi zisizo za polynomial. Kwa mfano, fikiria kazi ya kutafuta ufumbuzi wa\(\tan(x)−x=0.\) Hakuna formula rahisi ipo kwa ufumbuzi wa equation hii. Katika hali kama hizi, tunaweza kutumia njia ya Newton ili kukadiria mizizi.

Mbinu Newton inafanya matumizi ya wazo zifuatazo kwa takriban ufumbuzi wa\(f(x)=0.\) By sketching graph ya\(f\), tunaweza kukadiria mzizi wa\(f(x)=0\). Hebu tupige makadirio haya\(x_0\). Sisi kisha kuteka mstari tangent kwa\(f\) saa\(x_0\). Kama\(f′(x_0)≠0\), mstari huu tangent intersects\(x\) -axis wakati fulani\((x_1,0)\). Sasa hebu\(x_1\) kuwa makadirio ya pili kwa mizizi halisi. Kwa kawaida,\(x_1\) ni\(x_0\) karibu kuliko mizizi halisi. Halafu tunatoa mstari wa tangent hadi\(f\) saa\(x_1\). Kama\(f′(x_1)≠0\), mstari huu tangent pia intersects\(x\) -axis, kuzalisha makadirio mwingine,\(x_2\). Tunaendelea kwa njia hii, deriving orodha ya makadirio:\(x_0,\, x_1,\, x_2,\, ….\) Kwa kawaida, idadi\(x_0,\, x_1,\, x_2,\, …\) haraka mbinu mizizi halisi\(x^*\), kama inavyoonekana katika takwimu zifuatazo.

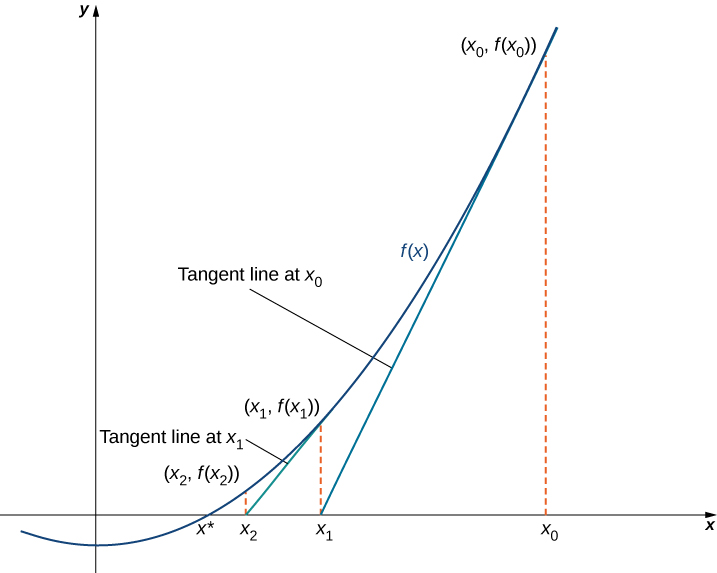
Kazi hii f (x) inayotolewa na pointi (x0, f (x0)), (x1, f (x1)), na (x2, f (x2)) alama juu ya kazi. Kutoka (x0, f (x0)), mstari wa tangent hutolewa, na hupiga mhimili x saa x1. Kutoka (x0, f (x0)), mstari wa tangent hutolewa, na hupiga mhimili x saa x2. Kama line tangent walikuwa inayotolewa kutoka (x2, f (x2)), inaonekana kwamba ingekuwa kuja karibu sana na x*, ambayo ni mizizi halisi. Kila mstari wa tangent inayotolewa kwa utaratibu huu unaonekana kupata karibu na karibu na x*. — \(\PageIndex{1}\)Kielelezo:makadirio mbinu\(x_0,\, x_1,\, x_2,\, … \) mizizi halisi.\(x^*\) makadirio ni inayotokana na kuangalia mistari tangent kwa graph ya\(f\).

Sasa hebu angalia jinsi ya kufanya mahesabu makadirio\(x_0,\, x_1,\, x_2,\, ….\) Kama\(x_0\) ni makadirio yetu ya kwanza, makadirio\(x_1\) hufafanuliwa kwa kuruhusu\((x_1,0)\) kuwa\(x\) -intercept ya mstari tangent kwa\(f\) saa\(x_0\). Ulinganisho wa mstari huu wa tangent hutolewa na

\[y=f(x_0)+f′(x_0)(x−x_0). \nonumber \]

Kwa hiyo,\(x_1\) lazima kukidhi

\[f(x_0)+f′(x_0)(x_1−x_0)=0.\nonumber \]

Kutatua equation hii kwa\(x_1\), tunahitimisha kuwa

\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}.\nonumber \]

Vile vile, hatua\((x_2,0)\) ni\(x\) -intercept ya mstari wa tangent kwa\(f\) saa\(x_1\). Kwa hiyo,\(x_2\) satisfies equation

\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}.\nonumber \]

Kwa ujumla, kwa\(n>0,x_n\) satisfies

\[x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}.\label{Newton} \]

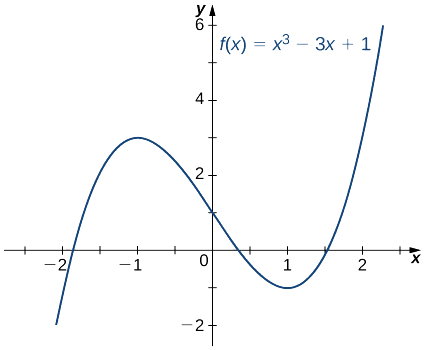
Halafu tunaona jinsi ya kutumia mbinu hii ili takriban mizizi ya polynomial\(f(x)=x^3−3x+1.\)

Mfano\(\PageIndex{1}\): Finding a Root of a Polynomial

Tumia njia ya Newton ili kukadiria mzizi wa\(f(x)=x^3−3x+1\) katika kipindi\([1,2]\). Hebu\(x_0=2\) na kupata\(x_1,\, x_2, \,x_3, \,x_4,\) na\(x_5\).

Suluhisho

Kutoka Kielelezo\(\PageIndex{2}\), tunaona kwamba\(f\) ina mizizi moja juu ya muda\([1,2]\). Kwa hiyo\(x_0=2\) inaonekana kama busara makadirio ya kwanza. Ili kupata makadirio ya, tunatumia Equation\ ref {Newton}. Tangu\(f(x)=x^3−3x+1\), derivative ni\(f′(x)=3x^2−3\). Kutumia Equation\ ref {Newton} na\(n=1\) (na calculator inayoonyesha\(10\) tarakimu), tunapata

\[x_1=x_0−\frac{f(x_0)}{f'(x_0)}=2−\frac{f(2)}{f'(2)}=2−\frac{3}{9}≈1.666666667.\nonumber \]

Ili kupata makadirio ya,\(x_2\), tunatumia Equation\ ref {Newton} na\(n=2\) na thamani ya\(x_1\) kuhifadhiwa kwenye calculator. Tunaona kwamba

\[x_2=x_1-\frac{f(x_1)}{f'(x_1)}≈1.548611111.\nonumber \]

Kuendelea kwa njia hii, tunapata matokeo yafuatayo:

\(x_1≈1.666666667\)
\(x_2≈1.548611111\)
\(x_3≈1.532390162\)
\(x_4≈1.532088989\)
\(x_5≈1.532088886\)
\(x_6≈1.532088886.\)

Tunaona kwamba tulipata thamani sawa\(x_5\) na\(x_6\). Kwa hiyo, matumizi yoyote ya baadaye ya njia ya Newton itawezekana kutoa thamani sawa\(x_n\).

Kazi f (x) = x3 - 3x + 1 hutolewa. Ina mizizi kati ya -1 na -1, 0 na 1, na 1 na 2. — Kielelezo\(\PageIndex{2}\): Kazi\(f(x)=x^3−3x+1\) ina mizizi moja juu ya muda\([1,2].\)

Zoezi\(\PageIndex{1}\)

Kuruhusu\(x_0=0\), hebu tutumie njia ya Newton ili takriban mizizi ya\(f(x)=x^3−3x+1\) zaidi ya muda\([0,1]\) kwa kuhesabu\(x_1\) na\(x_2\).

Kidokezo: Matumizi Equation\ ref {Newton}.

Jibu: \(x_1≈0.33333333\)
\(x_2≈0.347222222\)

Njia ya Newton pia inaweza kutumika kwa takriban mizizi ya mraba. Hapa tunaonyesha jinsi ya takriban\(\sqrt{2}\). Njia hii inaweza kubadilishwa ili takriban mizizi ya mraba ya nambari yoyote nzuri.

Mfano\(\PageIndex{2}\): Finding a Square Root

Tumia njia ya Newton kwa takriban\(\sqrt{2}\) (Kielelezo\(\PageIndex{3}\)). Hebu\(f(x)=x^2−2\), basi\(x_0=2\), na uhesabu\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). (Tunaona kwamba tangu\(f(x)=x^2−2\) ina sifuri saa\(\sqrt{2}\), thamani ya awali\(x_0=2\) ni chaguo nzuri kwa takriban\(\sqrt{2}\)).

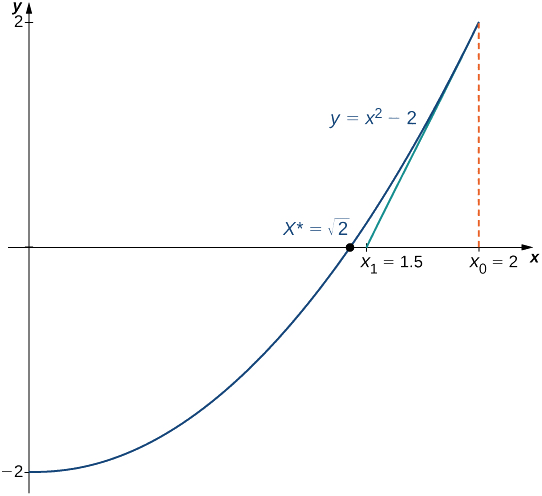
Kazi y = x2 - 2 hutolewa. Mstari uliopigwa unakuja kutoka x0 = 2, na mstari wa tangent hutolewa kutoka huko. Inagusa x1 = 1.5, ambayo iko karibu na x* = mizizi ya mraba ya 2. — Kielelezo\(\PageIndex{3}\): Tunaweza kutumia njia Newton ya kupata\(\sqrt{2}\).

Suluhisho

Kwa\(f(x)=x^2−2,\; f′(x)=2x.\) Kutoka Equation\ ref {Newton}, tunajua kwamba

\ [kuanza {align*} x_n&=x_ {n -1}}}\ frac {f (x_ {n -1})} {f' (x_ {n -1})}\\ [4pt]
&=x_ {n -1}}\\ frac {x^2_ {n -1} {n-1}}\\ 4pt]
&=\ frac {1} {2} x_ {n-1} +\ frac {1} {x_ {n-1}}\\ [4pt]
&=\ Frac {1} {2}\ kushoto (x_ {n-1} +\ frac {2} {x_ {n -1}}\ haki). \ mwisho {align*}\ nonumber\]

Kwa hiyo,

\(x_1=\frac{1}{2}\left(x_0+\frac{2}{x_0}\right)=\frac{1}{2}\left(2+\frac{2}{2}\right)=1.5\)

\(x_2=\frac{1}{2}\left(x_1+\frac{2}{x_1}\right)=\frac{1}{2}\left(1.5+\frac{2}{1.5}\right)≈1.416666667.\)

Kuendelea kwa njia hii, tunaona kwamba

\(x_1=1.5\)

\(x_2≈1.416666667\)

\(x_3≈1.414215686\)

\(x_4≈1.414213562\)

\(x_5≈1.414213562.\)

Kwa kuwa sisi kupatikana thamani sawa kwa\(x_4\) na\(x_5\), hakuna uwezekano kwamba thamani\(x_n\) itabadilika juu ya maombi yoyote baadae ya njia Newton. Sisi kuhitimisha kwamba\(\sqrt{2}≈1.414213562.\)

Zoezi\(\PageIndex{2}\)

Tumia njia ya Newton ili takriban\(\sqrt{3}\) kwa kuruhusu\(f(x)=x^2−3\) na\(x_0=3\). Kupata\(x_1\) na\(x_2\).

Kidokezo: Kwa\(f(x)=x^2−3\), equation\ ref {Newton} inapunguza kwa\(x_n=\frac{x_{n−1}}{2}+\frac{3}{2x_{n−1}}\).

Jibu: \(x_1=2\)
\(x_2=1.75\)

Wakati wa kutumia njia Newton ya, kila makadirio baada nadhani ya awali hufafanuliwa katika suala la makadirio ya awali kwa kutumia formula sawa. Hasa, kwa kufafanua kazi\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\), tunaweza kuandika upya Equation\ ref {Newton} kama\(x_n=F(x_{n−1})\). Aina hii ya mchakato, ambapo kila\(x_n\) ni defined katika suala la\(x_{n−1}\) kwa kurudia kazi hiyo, ni mfano wa mchakato iterative. Muda mfupi, sisi kuchunguza michakato mingine iterative. Kwanza, hebu tuangalie sababu kwa nini njia ya Newton inaweza kushindwa kupata mizizi.

Kushindwa kwa Njia ya Newton

Kwa kawaida, njia ya Newton hutumiwa kupata mizizi kwa haraka. Hata hivyo, mambo yanaweza kwenda vibaya. Baadhi ya sababu mbinu ya Newton inaweza kushindwa ni pamoja na yafuatayo:

Katika moja ya makadirio\(x_n\), derivative\(f′\) ni sifuri katika\(x_n\), lakini\(f(x_n)≠0\). Matokeo yake, mstari wa tangent wa\(f\) saa\(x_n\) hauingiliani\(x\) -axis. Kwa hiyo, hatuwezi kuendelea na mchakato wa iterative.
Makadirio\(x_0,\, x_1,\, x_2,\, …\) yanaweza kufikia mizizi tofauti. Ikiwa kazi\(f\) ina mizizi zaidi ya moja, inawezekana kwamba makadirio yetu hayakukaribia moja ambayo tunatafuta, lakini fikiria mizizi tofauti (angalia Mchoro\(\PageIndex{4}\)). Tukio hili mara nyingi hutokea wakati hatuwezi kuchagua makadirio\(x_0\) karibu kutosha kwa mizizi taka.
makadirio inaweza kushindwa mbinu mizizi kabisa. Katika Mfano\(\PageIndex{3}\), sisi kutoa mfano wa kazi na nadhani ya awali\(x_0\) kama kwamba makadirio mfululizo kamwe mbinu mizizi kwa sababu makadirio mfululizo kuendelea mbadala na kurudi kati ya maadili mawili.

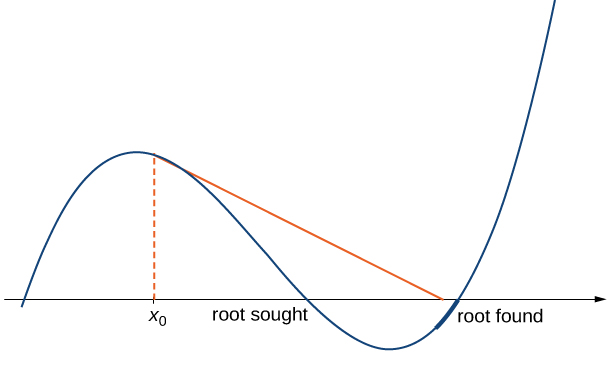
kazi ni inayotolewa na mizizi miwili, kinachoitwa mizizi walitaka na mizizi kupatikana. Hatua ya x0 imechaguliwa kama kwamba wakati tangent ya x0 inachukuliwa, ingawa iko karibu na mizizi inayotafutwa, pointi za tangent kwenye mizizi iliyopatikana. — Kielelezo\(\PageIndex{4}\): Kama nadhani ya awali\(x_0\) ni mbali sana na mizizi walitaka, inaweza kusababisha makadirio kwamba mbinu mizizi mbalimbali.

Mfano\(\PageIndex{3}\): When Newton’s Method Fails

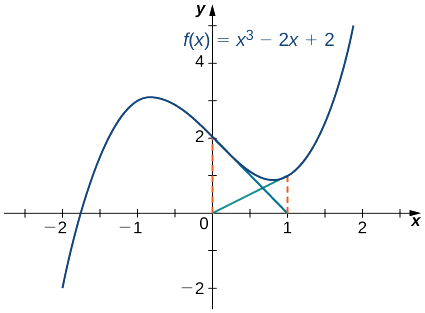
Fikiria kazi\(f(x)=x^3−2x+2\). Hebu\(x_0=0\). Onyesha kwamba mlolongo\(x_1,\, x_2,\, …\) inashindwa mbinu mzizi wa\(f\).

Suluhisho

Kwa\(f(x)=x^3−2x+2,\) derivative\(f′(x)=3x^2−2\) ni.Kwa hiyo,

\[x_1=x_0−\frac{f(x_0)}{f′(x_0)}=0−\frac{f(0)}{f′(0)}=−\frac{2}{−2}=1. \nonumber \]

Katika hatua inayofuata,

\[x_2=x_1−\frac{f(x_1)}{f'(x_1)}=1−\frac{f(1)}{f′(1)}=1−\frac{1}{1}=0. \nonumber \]

Kwa hiyo, idadi\(x_0,\, x_1,\, x_2,\, …\) kuendelea bounce na kurudi kati\(0\)\(1\) na kamwe kupata karibu na mizizi\(f\) ambayo ni zaidi ya muda\([−2,−1]\) (Kielelezo\(\PageIndex{5}\)). Kwa bahati nzuri, kama sisi kuchagua makadirio ya awali\(x_0\) karibu na mizizi halisi, tunaweza kuepuka hali hii.

Kazi f (x) = x3 - 2x + 2 hutolewa, ambayo ina mizizi kati ya -1 na -1. Tangent kutoka x = 0 inakwenda x = 1, na tangent kutoka x = 1 inakwenda x = 0. — Kielelezo\(\PageIndex{5}\): makadirio kuendelea mbadala kati\(0\)\(1\) na kamwe mbinu mzizi wa\(f\).

Zoezi\(\PageIndex{3}\)

Kwa\(f(x)=x^3−2x+2,\) basi\(x_0=−1.5\) na kupata\(x_1\) na\(x_2\).

Kidokezo: Matumizi Equation\ ref {Newton}.

Jibu: \(x_1≈−1.842105263\)
\(x_2≈−1.772826920\)

Kutoka Mfano\(\PageIndex{3}\), tunaona kwamba njia ya Newton haifanyi kazi kila wakati. Hata hivyo, wakati inafanya kazi, mlolongo wa makadirio hukaribia mizizi haraka sana. Majadiliano ya jinsi ya haraka mlolongo wa makadirio mbinu mizizi kupatikana kwa kutumia njia Newton ni pamoja na katika maandiko juu ya uchambuzi namba.

Michakato mingine ya Iterative

Kama ilivyoelezwa hapo awali, njia ya Newton ni aina ya mchakato wa iterative. Sisi sasa kuangalia mfano wa aina tofauti ya mchakato iterative.

Fikiria kazi\(F\) na namba ya awali\(x_0\). Eleza namba zinazofuata\(x_n\) kwa formula\(x_n=F(x_{n−1})\). Utaratibu huu ni mchakato iterative kwamba inajenga orodha ya idadi Orodha\(x_0,\, x_1,\, x_2,\, …,\, x_n,\, ….\) hii ya idadi inaweza mbinu idadi ya mwisho\(x^*\) kama\(n\) anapata kubwa, au inaweza. Katika Mfano\(\PageIndex{4}\), tunaona mfano wa kazi\(F\) na nadhani ya awali\(x_0\) kama kwamba orodha ya namba inayotokana inakaribia thamani ya mwisho.

Mfano\(\PageIndex{4}\): Finding a Limit for an Iterative Process

Hebu\(F(x)=\frac{1}{2}x+4\) na basi\(x_0=0\). Kwa wote\(n≥1\), basi\(x_n=F(x_{n−1})\). Pata maadili\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Kufanya dhana kuhusu nini kinatokea kwa orodha hii ya idadi\(x_1,\, x_2,\, x_3,\, …,\, x_n,\, …\) kama\(n→∞\). Ikiwa orodha ya namba\(x_1,\, x_2,\, x_3,\, …\) inakaribia nambari ya mwisho\(x^*\), kisha\(x^*\) inatimiza\(x^*=F(x^*)\), na\(x^*\) inaitwa hatua ya kudumu ya\(F\).

Suluhisho

Ikiwa\(x_0=0\), basi

\(x_1=\frac{1}{2}(0)+4=4\)
\(x_2=\frac{1}{2}(4)+4=6\)
\(x_3=\frac{1}{2}(6)+4=7\)
\(x_4=\frac{1}{2}(7)+4=7.5\)
\(x_5=\frac{1}{2}(7.5)+4=7.75\)
\(x_6=\frac{1}{2}(7.75)+4=7.875\)
\(x_7=\frac{1}{2}(7.875)+4=7.9375\)
\(x_8=\frac{1}{2}(7.9375)+4=7.96875\)
\(x _9=\frac{1}{2}(7.96875)+4=7.984375.\)

Kutoka kwenye orodha hii, tunadhani kwamba maadili\(x_n\) yanakaribia\(8\).

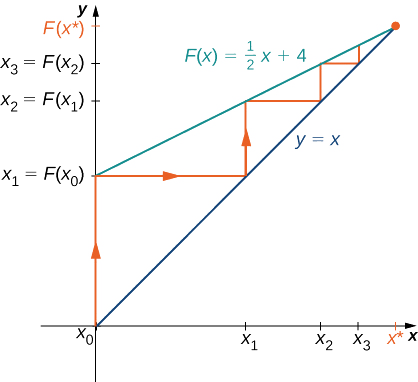
Kielelezo\(\PageIndex{6}\) hutoa hoja graphical kwamba maadili mbinu\(8\) kama\(n→∞\). Kuanzia wakati huo\((x_0,x_0)\), tunapata mstari wa wima hadi hatua\((x_0,F(x_0))\). Nambari inayofuata katika orodha yetu ni\(x_1=F(x_0)\). \(x_1\)Tunatumia kuhesabu\(x_2\). Kwa hiyo, tunapata mstari usio na usawa unaounganisha\((x_0,x_1)\)\((x_1,x_1)\) kwenye mstari\(y=x\), na kisha kuteka mstari wa wima unaounganisha\((x_1,x_1)\) hadi hatua\((x_1,F(x_1))\). Pato\(F(x_1)\) inakuwa\(x_2\). Kuendelea kwa njia hii, tunaweza kuunda idadi isiyo na kipimo ya makundi ya mstari. Makundi haya line ni trapped kati ya mistari\(F(x)=\frac{x}{2}+4\) na\(y=x\). Makundi ya mstari yanakaribia karibu na hatua ya makutano ya mistari hii miwili, ambayo hutokea wakati\(x=F(x)\). Kutatua equation\(x=\frac{x}{2}+4,\) sisi kuhitimisha wao intersect katika\(x=8\). Kwa hiyo, ushahidi wetu wa kielelezo unakubaliana na ushahidi wetu wa namba kwamba orodha ya namba\(x_0,\, x_1,\, x_2,\, …\) inakaribia\(x^*=8\) kama\(n→∞\).

Kazi F (x) = (1/2) x + 4 imewekwa pamoja na y = x Kutoka x0, ambayo inaonekana kuwa asili, mstari hutolewa kwa kazi F (x) saa x1 = F (x0). Kisha mstari hutolewa kwa haki kutoka hapa hadi mstari y = x, ambapo mstari unafanywa hadi x2 = F (x1). Kisha mstari hutolewa kwa haki kutoka hapa hadi mstari y = x, ambapo mstari unafanywa hadi x3 = F (x2). Kuendelea mchakato huu ingekuwa hujiunga kwenye mistari miwili 'makutano uhakika katika x* = 8. — Kielelezo\(\PageIndex{6}\): Mchakato huu iterative mbinu thamani\(x^*=8.\)

Zoezi\(\PageIndex{4}\)

Fikiria kazi\(F(x)=\frac{1}{3}x+6\). Hebu\(x_0=0\) na basi\(x_n=F(x_{n−1})\) kwa\(n≥2\). Kupata\(x_1,\, x_2,\, x_3,\, x_4,\, x_5\). Kufanya dhana kuhusu nini kinatokea kwa orodha ya idadi\(x_1,\, x_2,\, x_3,\, …\, x_n,\, … \) kama\(n→∞.\)

Kidokezo: Fikiria hatua ambapo mistari\(y=x\) na\(y=F(x)\) intersect.

Jibu: \(x_1=6,\;x_2=8,\;x_3=\frac{26}{3},\;x_4=\frac{80}{9},\;x_5=\frac{242}{27};\;x^*=9\)

Utaratibu wa Iterative na machafuko

Michakato ya iterative inaweza kutoa tabia fulani ya kuvutia sana. Katika sehemu hii, tumeona mifano kadhaa ya michakato iterative kwamba hujiunga na uhakika fasta. Pia tuliona katika Mfano\(\PageIndex{3}\) kwamba mchakato iterative bounced na kurudi kati ya maadili mawili. Tunaita aina hii ya tabia ya mzunguko wa 2. Michakato ya iterative inaweza kugeuka kwa mzunguko na periodicities mbalimbali, kama vile mzunguko wa 2, mzunguko wa 4 (ambapo mchakato wa iterative unarudia mlolongo wa maadili manne), mzunguko wa 8, na kadhalika.

Baadhi ya michakato iterative mavuno nini wanahisabati wito machafuko. Katika kesi hiyo, mchakato iterative anaruka kutoka thamani kwa thamani katika mtindo inaonekana random na kamwe converges au kutatua katika mzunguko. Ingawa utafutaji kamili wa machafuko ni zaidi ya upeo wa maandishi haya, katika mradi huu tunaangalia moja ya mali muhimu ya mchakato wa machafuko iterative: utegemezi nyeti juu ya hali ya awali. Mali hii inahusu dhana kwamba mabadiliko madogo katika hali ya awali yanaweza kuzalisha tabia tofauti sana katika mchakato wa iterative.

Pengine bora inayojulikana mfano wa machafuko ni kuweka Mandelbrot (tazama Kielelezo\(\PageIndex{7}\)), jina lake baada ya Benoit Mandelbrot (1924—2010), ambaye alichunguza mali zake na kusaidiwa popularize uwanja wa nadharia machafuko. Kuweka Mandelbrot ni kawaida yanayotokana na kompyuta na inaonyesha maelezo ya kuvutia juu ya utvidgningen, ikiwa ni pamoja na binafsi replication ya kuweka. Matoleo kadhaa ya rangi ya kuweka yameonyeshwa kwenye makumbusho na yanaweza kupatikana mtandaoni na katika vitabu maarufu juu ya somo.

Fractal ngumu sana na ya kikaboni. — Kielelezo\(\PageIndex{7}\): Kuweka Mandelbrot ni mfano maalumu wa seti ya pointi yanayotokana na tabia ya machafuko ya iterative ya kazi rahisi.

Katika mradi huu tunatumia ramani ya vifaa

\[f(x)=rx(1−x) \nonumber \]

wapi\(x∈[0,1]\) na\(r>0\)

kama kazi katika mchakato wetu iterative. Ramani ya vifaa ni kazi ya udanganyifu rahisi; lakini, kulingana na thamani ya\(r\), mchakato wa iterative unaosababisha unaonyesha tabia fulani ya kuvutia sana. Inaweza kusababisha pointi zilizowekwa, mzunguko, na hata machafuko.

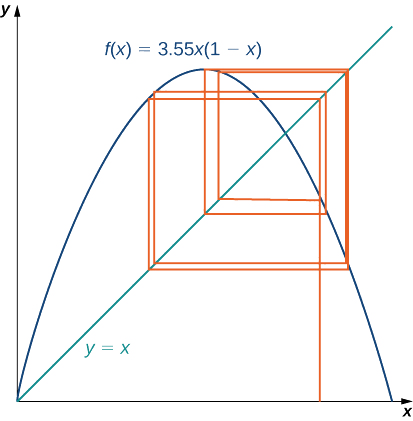
Ili kutazama tabia ya muda mrefu ya mchakato wa iterative unaohusishwa na ramani ya vifaa, tutatumia chombo kinachoitwa mchoro wa utando. Kama tulivyofanya na mchakato iterative sisi kuchunguza mapema katika sehemu hii, sisi kwanza kuteka mstari wima kutoka hatua\((x_0,0)\) kwa uhakika\((x_0,f(x_0))=(x_0,x_1)\). Sisi kisha kuteka mstari usawa kutoka hatua hiyo kwa uhakika\((x_1,x_1),\) kisha kuteka mstari wima kwa\((x_1,f(x_1))=(x_1,x_2)\), na kuendelea na mchakato mpaka tabia ya muda mrefu ya mfumo inakuwa dhahiri. Kielelezo\(\PageIndex{8}\) inaonyesha tabia ya muda mrefu ya ramani vifaa wakati\(r=3.55\) na\(x_0=0.2\). (\(100\)iterations kwanza si njama.) tabia ya muda mrefu ya mchakato huu iterative ni\(8\) -mzunguko.

Katika roboduara ya kwanza, f (x) = 3.55x (1 — x) imewekwa kama y = x Kutoka hatua fulani kwenye mstari wa x, mstari unafanywa hadi mstari y = x, ambapo hatua inageuka kuwa ya usawa na inaendelea mpaka inagusa makali ya nje ya f (x), wakati ambapo inageuka tena kuwa wima mpaka kila mstari y = x. mchakato inaendelea idadi ya mara na inajenga mfululizo wa masanduku ya kuvutia. — Kielelezo\(\PageIndex{8}\): Mchoro wa cobweb\(f(x)=3.55x(1−x)\) unawasilishwa hapa. Mlolongo wa maadili husababisha mzunguko wa 8.

Hebu\(r=0.5\) na uchague\(x_0=0.2\). Labda kwa mkono au kwa kutumia kompyuta, uhesabu\(10\) maadili ya kwanza katika mlolongo. Je, mlolongo unaonekana kugeuka? Ikiwa ndivyo, kwa thamani gani? Je! Inasababisha mzunguko? Ikiwa ndivyo, ni aina gani ya mzunguko (kwa mfano\(2\), -mzunguko,\(4\) -mzunguko.)?
Ni nini kinachotokea wakati\(r=2\)?
Kwa\(r=3.2\) na\(r=3.5\), mahesabu ya maadili ya kwanza ya\(100\) mlolongo. Kuzalisha mchoro cobweb kwa kila mchakato iterative. (Applets kadhaa za bure zinapatikana mtandaoni zinazozalisha michoro za utando wa ramani ya vifaa.) Tabia ya muda mrefu katika kila kesi hizi ni nini?
Sasa hebu\(r=4.\) Tumia maadili ya\(100\) mlolongo wa kwanza na uzalishe mchoro wa cobweb. Tabia ya muda mrefu katika kesi hii ni nini?
Rudia mchakato kwa\(r=4,\) lakini basi\(x_0=0.201.\) Jinsi gani tabia hii kulinganisha na tabia kwa\(x_0=0.2\)?

Dhana muhimu

Mbinu Newton ya approximates mizizi ya\(f(x)=0\) kwa kuanzia na makadirio ya awali\(x_0\), kisha anatumia mistari tangent kwa graph ya\(f\) kujenga mlolongo wa makadirio\(x_1,\, x_2,\, x_3,\, ….\)
Kwa kawaida, njia ya Newton ni njia bora ya kutafuta mizizi fulani. Katika hali fulani, mbinu ya Newton inashindwa kufanya kazi kwa sababu orodha ya namba\(x_0,\, x_1,\, x_2,\, …\) haipatikani thamani ya mwisho au inakaribia thamani nyingine isipokuwa mzizi uliotafutwa.
Mchakato wowote ambao orodha ya namba\(x_0,\, x_1,\, x_2,\, …\) huzalishwa kwa kufafanua namba ya awali\(x_0\) na kufafanua namba zinazofuata na equation\(x_n=F(x_{n−1})\) kwa kazi fulani\(F\) ni mchakato wa iterative. Mbinu Newton ni mfano wa mchakato iterative, ambapo kazi\(F(x)=x−\left[\frac{f(x)}{f′(x)}\right]\) kwa ajili ya kazi fulani\(f\).

faharasa

mchakato wa kurudia: mchakato ambao orodha ya namba\(x_0,x_1,x_2,x_3…\) huzalishwa kwa kuanzia na idadi\(x_0\) na kufafanua\(x_n=F(x_{n−1})\)\(n≥1\)

Njia ya Newton: njia ya kukadiria mizizi ya\(f(x)=0;\) kutumia nadhani ya awali\(x_0\); kila makadirio baadae hufafanuliwa na equation\(x_n=x_{n−1}−\frac{f(x_{n−1})}{f'(x_{n−1})}\)