4.8: Utawala wa L'Hôpital

Malengo ya kujifunza

• Tambua wakati wa kutumia utawala wa L'Hôpital.
• Kutambua aina indeterminate zinazozalishwa na quotients, bidhaa, subtractions, na nguvu, na kutumia utawala wa L'Hôpital katika kila kesi.
• Eleza viwango vya ukuaji wa jamaa wa kazi.

Katika sehemu hii, tunachunguza chombo chenye nguvu cha kutathmini mipaka. Chombo hiki, kinachojulikana kama utawala wa L'Hôpital, hutumia derivatives kuhesabu mipaka. Kwa sheria hii, tutaweza kutathmini mipaka mingi ambayo hatujaweza kuamua. Badala ya kutegemea ushahidi wa namba kwa dhana kwamba kikomo kipo, tutaweza kuonyesha kwa uhakika kwamba kikomo kipo na kuamua thamani yake halisi.

Kutumia Kanuni ya L'Hôpital

Utawala wa L'Hôpital unaweza kutumika kutathmini mipaka inayohusisha quotient ya kazi mbili. Fikiria

\[\lim_{x→a}\dfrac{f(x)}{g(x)}. \nonumber \]

Kama\(\displaystyle \lim_{x→a}f(x)=L_1\) na\(\displaystyle \lim_{x→a}g(x)=L_2≠0,\) kisha

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{L_1}{L_2}. \nonumber \]

Hata hivyo, ni nini kinachotokea ikiwa\(\displaystyle \lim_{x→a}f(x)=0\) na\(\displaystyle \lim_{x→a}g(x)=0\)? Tunaita hii moja ya fomu indeterminate, ya aina\(\dfrac{0}{0}\). Hii inachukuliwa kuwa fomu isiyo ya kawaida kwa sababu hatuwezi kuamua tabia halisi ya\(\dfrac{f(x)}{g(x)}\) kama\(x→a\) bila uchambuzi zaidi. Tumeona mifano ya hii mapema katika maandishi. Kwa mfano, fikiria

\[\lim_{x→2}\dfrac{x^2−4}{x−2} \nonumber \]

na

\[\lim_{x→0}\dfrac{\sin x}{x}.\nonumber \]

Kwa mifano ya kwanza ya hizi, tunaweza kutathmini kikomo kwa kuzingatia nambari na kuandika

\[\lim_{x→2}\dfrac{x^2−4}{x−2}=\lim_{x→2}\dfrac{(x+2)(x−2)}{x−2}=\lim_{x→2}(x+2)=2+2=4. \nonumber \]

Kwa maana\(\displaystyle \lim_{x→0}\dfrac{\sin x}{x}\) tulikuwa na uwezo wa kuonyesha, kwa kutumia hoja ya kijiometri, kwamba

\[\lim_{x→0}\dfrac{\sin x}{x}=1. \nonumber \]

Hapa tunatumia mbinu tofauti za kutathmini mipaka kama hizi. Sio tu mbinu hii inatoa njia rahisi ya kutathmini mipaka hii, lakini pia, na muhimu zaidi, inatupa njia ya kutathmini mipaka mingine mingi ambayo hatukuweza kuhesabu hapo awali.

Wazo nyuma ya utawala wa L'Hôpital unaweza kuelezewa kwa kutumia makadirio ya ndani ya mstari. Fikiria kazi mbili za\(f\) kutofautisha\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) na vile vile vile\(g′(a)≠0\) Kwa\(x\) karibu\(a\), tunaweza kuandika\(g\)

\[f(x)≈f(a)+f′(a)(x−a) \nonumber \]

na

\[g(x)≈g(a)+g′(a)(x−a). \nonumber \]

Kwa hiyo,

\[\dfrac{f(x)}{g(x)}≈\dfrac{f(a)+f′(a)(x−a)}{g(a)+g′(a)(x−a)}. \nonumber \]

Kielelezo\(\PageIndex{1}\): Ikiwa\(\displaystyle\lim_{x→a}f(x)=\lim_{x→a}g(x)\), basi uwiano\(f(x)/g(x)\) ni takriban sawa na uwiano wa makadirio yao ya mstari karibu\(a\).

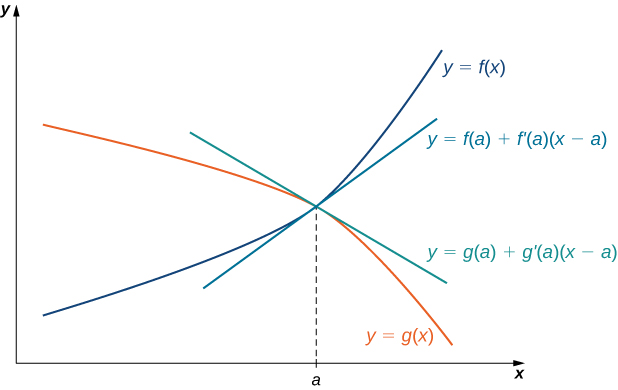
Tangu\(f\) ni differentiable katika\(a\), basi\(f\) ni kuendelea katika\(a\), na kwa hiyo\(\displaystyle f(a)=\lim_{x→a}f(x)=0\). Vile vile,\(\displaystyle g(a)=\lim_{x→a}g(x)=0\). Kama sisi pia kudhani kwamba\(f′\) na\(g′\) ni kuendelea katika\(x=a\), basi\(\displaystyle f′(a)=\lim_{x→a}f′(x)\) na\(\displaystyle g′(a)=\lim_{x→a}g′(x)\). Kutumia mawazo haya, tunahitimisha kuwa

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)(x−a)}{g′(x)(x−a)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} . \nonumber \]

Kumbuka kuwa dhana kwamba\(f′\) na\(g′\) ni kuendelea katika\(a\) na\(g′(a)≠0\) inaweza kuwa loosened. Tunasema utawala wa L'Hôpital rasmi kwa fomu isiyo ya kawaida\(\dfrac{0}{0}\). Pia kumbuka kuwa nukuu\(\dfrac{0}{0}\) haimaanishi sisi ni kweli kugawa sifuri kwa sifuri. Badala yake, sisi ni kutumia notation\(\dfrac{0}{0}\) kuwakilisha quotient ya mipaka, ambayo kila mmoja ni sifuri.

Utawala wa L'Hôpital (0/0 Uchunguzi)

Tuseme\(f\) na\(g\) ni differentiable kazi juu ya muda wazi zenye\(a\), ila uwezekano katika\(a\). Kama\(\displaystyle \lim_{x→a}f(x)=0\) na\(\displaystyle \lim_{x→a}g(x)=0,\) kisha

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}, \nonumber \]

kuchukua kikomo juu ya haki ipo au ni\(∞\) au\(−∞\). Matokeo haya pia ana kama sisi ni kuzingatia mipaka upande mmoja, au kama\(a=∞\) au\(a=−∞.\)

Ushahidi

Sisi kutoa ushahidi wa theorem hii katika kesi maalum wakati\(f,g,f′,\) na wote\(g′\) ni kuendelea juu ya muda wazi zenye\(a\). Katika hali hiyo, tangu\(\displaystyle\lim_{x→a}f(x)=0=\lim_{x→a}g(x)\)\(f\) na\(g\) ni kuendelea katika\(a\), inafuata kwamba\(f(a)=0=g(a)\). Kwa hiyo,

\ [kuanza {align*}\ lim_ {x→ a}\ dfrac {f (x)} {g (x)} &=\ lim_ {x → a}\ dfrac {f (x) -f (a)} {g (x) -g (a)} & &\ maandishi {Tangu}\, f (a) =0=g (a)\\ [4pt]
&=\ lim_ {x→ a}\ dfrac {f (x) -f (a)} {x-a}} {\ dfrac {g (x) -g (a)} {x-a}} & &\ maandishi {Kuzidisha nambari na denominator kwa}\,\ frac {1} {x-a}\\ [4pt]
&=\ frac {\ displaystyle\ lim_ {x→ a}\ dfrac {f (x) -f (a)} {x-a}} {\ displaystyle\ lim_ {x→ a}\ dfrac {g (x) -g (a)} {x-a}} & &\ maandishi {Kikomo cha quotient ni quotient ya mipaka.}\\ [4pt]
&=\ dfrac {f′ (a)} {g( a)} & &\ maandishi {Kwa ufafanuzi wa derivative}\\ [4pt]
&=\ frac {\ displaystyle\ lim_ {x→ a} f′ (x)} {\ displaystyle\ lim_ {x→ a} g (x)} & &\ maandishi {Kwa mwendelezo wa}\, f\,\ maandishi {na}\, g\\ [4pt]
&=\ lim_ {x→ a}\ dfrac {f′ (x)} {g( x)}. & &\ maandishi {kikomo cha quotient}\ mwisho {align*}\]

Kumbuka kuwa utawala wa L'Hôpital unasema tunaweza kuhesabu kikomo cha quotient\(\dfrac{f}{g}\) kwa kuzingatia kikomo cha quotient ya derivatives\(\dfrac{f′}{g′}\). Ni muhimu kutambua kwamba hatuwezi kuhesabu derivative ya quotient\(\dfrac{f}{g}\).

□

Mfano\(\PageIndex{1}\): Applying L’Hôpital’s Rule (0/0 Case)

Tathmini kila moja ya mipaka ifuatayo kwa kutumia utawala wa L'Hôpital.

1. \(\displaystyle \lim_{x→0}\dfrac{1−\cos x}{x}\)
2. \(\displaystyle \lim_{x→1}\dfrac{\sin(πx)}{\ln x}\)
3. \(\displaystyle \lim_{x→∞}\dfrac{e^{1/x}−1}{1/x}\)
4. \(\displaystyle \lim_{x→0}\dfrac{\sin x−x}{x^2}\)

Suluhisho

a Tangu namba\(1−\cos x→0\) na denominator\(x→0\), tunaweza kutumia utawala wa L'Hôpital kutathmini kikomo hiki. Tuna

\[\lim_{x→0}\dfrac{1−\cos x}{x}=\lim_{x→0}\dfrac{\dfrac{d}{dx}\big(1−\cos x\big)}{\dfrac{d}{dx}\big(x\big)}=\lim_{x→0}\dfrac{\sin x}{1}=\frac{\displaystyle \lim_{x→0}\sin x}{\displaystyle \lim_{x→0}1}=\dfrac{0}{1}=0. \nonumber \]

b Kama\(x→1,\) nambari\(\sin(πx)→0\) na denominator\(\ln(x)→0.\) Kwa hiyo, tunaweza kutumia utawala wa L'Hôpital. Tunapata

\[\begin{align*} \lim_{x→1}\dfrac{\sin(πx)}{\ln x}&=\lim_{x→1}\dfrac{π \cos(πx)}{1/x} \\[4pt] &=\lim_{x→1}(πx)\cos(πx) \\[4pt] &=(π⋅1)(−1)=−π. \end{align*} \nonumber \]

c. kama\(x→∞\), nambari\(e^{1/x}−1→0\) na denominator\(\frac{1}{x}→0\). Kwa hiyo, tunaweza kutumia utawala wa L'Hôpital. Tunapata

\[\lim_{x→∞}\dfrac{e^{1/x}−1}{\dfrac{1}{x}}=\lim_{x→∞}\dfrac{e^{1/x}(\tfrac{−1}{x^2})}{\left(\frac{−1}{x^2}\right)}=\lim_{x→∞}e^{1/x}=e^0=1. \nonumber \]

d Kama\(x→0,\) wote nambari na denominator mbinu sifuri. Kwa hiyo, tunaweza kutumia utawala wa L'Hôpital. Tunapata

\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=\lim_{x→0}\dfrac{\cos x−1}{2x}.\nonumber \]

Tangu kadiri na denominator ya quotient hii mpya wote mbinu sifuri kama\(x→0\), tunatumia utawala wa L'Hôpital tena. Kwa kufanya hivyo, tunaona kwamba

\[\lim_{x→0}\dfrac{\cos x−1}{2x}=\lim_{x→0}\dfrac{−\sin x}{2}=0. \nonumber \]

Kwa hiyo, tunahitimisha kuwa

\[\lim_{x→0}\dfrac{\sin x−x}{x^2}=0. \nonumber \]

Zoezi\(\PageIndex{1}\)

Tathmini\[\lim_{x→0}\dfrac{x}{\tan x}. \nonumber \]

Kidokezo

\(\dfrac{d}{dx}\big(\tan x\big)=\sec^2x\)

Jibu

\(1\)

Tunaweza pia kutumia utawala wa L'Hôpital kutathmini mipaka ya\(\dfrac{f(x)}{g(x)}\) quotients ambayo\(f(x)→±∞\) na\(g(x)→±∞\). Mipaka ya fomu hii imewekwa kama aina za aina isiyo ya kawaida\(∞/∞\). Tena, kumbuka kuwa sisi si kweli kugawa\(∞\) na\(∞\). Kwa kuwa\(∞\) si idadi halisi, hiyo haiwezekani; badala,\(∞/∞\) hutumiwa kuwakilisha quotient ya mipaka, ambayo kila mmoja ni\(∞\) au\(−∞\).

Utawala wa L'Hôpital (\(∞/∞\) Case)

Tuseme\(f\) na\(g\) ni differentiable kazi juu ya muda wazi zenye\(a\), ila uwezekano katika\(a\). Tuseme\(\displaystyle\lim_{x→a}f(x)=∞\) (au\(−∞\)) na\(\displaystyle\lim_{x→a}g(x)=∞\) (au\(−∞\)). Kisha,

\[\lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)} \nonumber \]

kuchukua kikomo juu ya haki ipo au ni\(∞\) au\(−∞\). Matokeo haya pia ana kama kikomo ni usio, ikiwa\(a=∞\) au\(−∞\), au kikomo ni upande mmoja.

Mfano\(\PageIndex{2}\): Applying L’Hôpital’s Rule (\(∞/∞\)) Case

Tathmini kila moja ya mipaka ifuatayo kwa kutumia utawala wa L'Hôpital.

1. \(\displaystyle\lim_{x→\infty}\dfrac{3x+5}{2x+1}\)
2. \(\displaystyle \lim_{x→0^+}\dfrac{\ln x}{\cot x}\)

Suluhisho

a. tangu\(3x+5\) and \(2x+1\) are first-degree polynomials with positive leading coefficients, \(\displaystyle\lim_{x→∞}(3x+5)=∞\) and \(\displaystyle\lim_{x→∞}(2x+1)=∞\). Therefore, we apply L’Hôpital’s rule and obtain

\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3}{2}=\dfrac{3}{2}.\nonumber \]

Kumbuka kuwa kikomo hiki kinaweza pia kuhesabiwa bila kuomba utawala wa L'Hôpital. Mapema katika sura tulionyesha jinsi ya kutathmini kikomo hicho kwa kugawanya nambari na denominator kwa nguvu ya juu ya x katika denominator. Kwa kufanya hivyo, tuliona kwamba

\[\lim_{x→∞}\dfrac{3x+5}{2x+1}=\lim_{x→∞}\dfrac{3+5/x}{2+1/x}=\dfrac{3}{2}. \nonumber \]

Utawala wa L'Hôpital unatupa njia mbadala za kutathmini aina hii ya kikomo.

b. hapa,\(\displaystyle \lim_{x→0^+}\ln x=−∞\) na\(\displaystyle \lim_{x→0^+}\cot x=∞\). Kwa hiyo, tunaweza kutumia utawala wa L'Hôpital na kupata

\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=\lim_{x→0^+}\dfrac{1/x}{−\csc^2x}=\lim_{x→0^+}\dfrac{1}{−x \csc^2x}. \nonumber \]

Sasa kama\(x→0^+, \csc^2x→∞\). Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In such a case, anything can happen with the product. Therefore, we cannot make any conclusion yet. To evaluate the limit, we use the definition of \(\csc x\) to write

\[\lim_{x→0^+}\dfrac{1}{−x \csc^2x}=\lim_{x→0^+}\dfrac{\sin^2x}{−x}. \nonumber \]

Sasa\(\displaystyle\lim_{x→0^+}\sin^2x=0\) and \(\displaystyle\lim_{x→0^+}-x=0\), so we apply L’Hôpital’s rule again. We find

\[\lim_{x→0^+}\dfrac{\sin^2x}{−x}=\lim_{x→0^+}\dfrac{2\sin x\cos x}{−1}=\dfrac{0}{−1}=0. \nonumber \]

Sisi kuhitimisha kwamba

\[\lim_{x→0^+}\dfrac{\ln x}{\cot x}=0. \nonumber \]

Zoezi\(\PageIndex{2}\)

Tathmini\[\lim_{x→∞}\dfrac{\ln x}{5x}. \nonumber \]

Kidokezo

\(\dfrac{d}{dx}\big(\ln x\big)=\dfrac{1}{x}\)

Jibu

\(0\)

Kama ilivyoelezwa, utawala wa L'Hôpital ni chombo muhimu sana cha kutathmini mipaka. Ni muhimu kukumbuka, hata hivyo, kwamba kuomba utawala wa L'Hôpital kwa quotient\(\dfrac{f(x)}{g(x)}\), it is essential that the limit of \(\dfrac{f(x)}{g(x)}\) be of the form \(\dfrac{0}{0}\) or \(∞/∞\). Consider the following example.

Mfano\(\PageIndex{3}\): When L’Hôpital’s Rule Does Not Apply

Fikiria\(\displaystyle\lim_{x→1}\dfrac{x^2+5}{3x+4}.\)

Onyesha kuwa kikomo hakiwezi kutathminiwa kwa kutumia utawala wa L'Hôpital.

Suluhisho

Kwa sababu mipaka ya nambari na denominator sio sifuri na sio wote usio na mwisho, hatuwezi kutumia utawala wa L'Hôpital. Kama sisi kujaribu kufanya hivyo, sisi kupata

\[\dfrac{d}{dx}(x^2+5)=2x\nonumber \]

na

\[\dfrac{d}{dx}(3x+4)=3. \nonumber \]

Katika hatua ambayo tunataka kuhitimisha kimakosa kwamba

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\lim_{x→1}\dfrac{2x}{3}=\dfrac{2}{3}. \nonumber \]

Hata hivyo, tangu\(\displaystyle \lim_{x→1}(x^2+5)=6\) na\(\displaystyle \lim_{x→1}(3x+4)=7,\) sisi kwa kweli

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}=\dfrac{6}{7}. \nonumber \]

Tunaweza kuhitimisha kwamba

\[\lim_{x→1}\dfrac{x^2+5}{3x+4}≠\lim_{x→1}\dfrac{\dfrac{d}{dx}(x^2+5)}{\dfrac{d}{dx}(3x+4).} \nonumber \]

Zoezi\(\PageIndex{3}\)

Eleza kwa nini hatuwezi kutumia utawala wa L'Hôpital kutathmini\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\). Tathmini\(\displaystyle\lim_{x→0^+}\dfrac{\cos x}{x}\) kwa njia nyingine.

Kidokezo

Kuamua mipaka ya nambari na denominator tofauti.

Jibu

\(\displaystyle\lim_{x→0^+}\cos x=1.\)Kwa hiyo, hatuwezi kutumia utawala wa L'Hôpital. Kikomo cha quotient ni\(∞.\)

Aina zingine za Indeterminate

Utawala wa L'Hôpital ni muhimu sana kwa kutathmini mipaka inayohusisha fomu zisizojulikana\(\dfrac{0}{0}\) na\(∞/∞\). Hata hivyo, tunaweza pia kutumia utawala wa L'Hôpital ili kusaidia kutathmini mipaka inayohusisha aina zingine zisizojulikana zinazotokea wakati wa kutathmini mipaka. Maneno\(0⋅∞, ∞−∞, 1^∞, ∞^0\), na yote\(0^0\) yanafikiriwa fomu zisizojulikana. Maneno haya si namba halisi. Badala yake, wao huwakilisha fomu zinazotokea wakati wa kujaribu kutathmini mipaka fulani. Halafu tunatambua kwa nini hizi ni fomu zisizojulikana na kisha kuelewa jinsi ya kutumia utawala wa L'Hôpital katika kesi hizi. Wazo muhimu ni kwamba ni lazima kuandika upya aina indeterminate kwa namna ambayo sisi kufika katika fomu indeterminate\(\dfrac{0}{0}\) au\(∞/∞\).

Aina isiyo ya kawaida ya Aina ya 0Δ

Tuseme tunataka kutathmini\(\displaystyle \lim_{x→a}(f(x)⋅g(x))\), wapi\(f(x)→0\) na\(g(x)→∞\) (au\(−∞\)) kama\(x→a\). Kwa kuwa muda mmoja katika bidhaa unakaribia sifuri, lakini neno lingine linakuwa kubwa kwa kiasi kikubwa (kwa ukubwa), chochote kinaweza kutokea kwa bidhaa. Tunatumia notation\(0⋅∞\) ili kutaja fomu inayotokea katika hali hii. kujieleza\(0⋅∞\) ni kuchukuliwa indeterminate kwa sababu hatuwezi kuamua bila uchambuzi zaidi tabia halisi ya bidhaa\(f(x)g(x)\) kama\(x→∞\). Kwa mfano, hebu\(n\) kuwa integer chanya na fikiria

\(f(x)=\dfrac{1}{(x^n+1)}\)na\(g(x)=3x^2\).

Kama\(x→∞, f(x)→0\) na\(g(x)→∞\). Hata hivyo, kikomo kama\(x→∞\) ya\(f(x)g(x)=\dfrac{3x^2}{(x^n+1)}\) inatofautiana, kulingana na\(n\). Ikiwa\(n=2\), basi\(\displaystyle\lim_{x→∞}f(x)g(x)=3\). Ikiwa\(n=1\), basi\(\displaystyle\lim_{x→∞}f(x)g(x)=∞\). Ikiwa\(n=3\), basi\(\displaystyle\lim_{x→∞}f(x)g(x)=0\). Hapa tunazingatia kikomo kingine kinachohusisha fomu isiyo ya kawaida\(0⋅∞\) na kuonyesha jinsi ya kuandika upya kazi kama quotient kutumia utawala wa L'Hôpital.

Mfano\(\PageIndex{4}\): Indeterminate Form of Type \(0⋅∞\)

Tathmini\(\displaystyle \lim_{x→0^+}x\ln x.\)

Suluhisho

Kwanza, andika upya kazi\(x\ln x\) kama quotient kuomba utawala wa L'Hôpital. Kama sisi kuandika

\[x\ln x=\dfrac{\ln x}{1/x} \nonumber \]

tunaona kwamba\(\ln x→−∞\) kama\(x→0^+\) na\(\dfrac{1}{x}→∞\) kama\(x→0^+\). Kwa hiyo, tunaweza kutumia utawala wa L'Hôpital na kupata

\[\lim_{x→0^+}\dfrac{\ln x}{1/x}=\lim_{x→0^+}\dfrac{\dfrac{d}{dx}\big(\ln x\big)}{\dfrac{d}{dx}\big(1/x\big)}=\lim_{x→0^+}\dfrac{1/x}{−1/x^2}=\lim_{x→0^+}(−x)=0. \nonumber \]

Sisi kuhitimisha kwamba

\[\lim_{x→0^+}x\ln x=0. \nonumber \]

Kielelezo\(\PageIndex{2}\): Kutafuta kikomo\(x=0\) cha kazi\(f(x)=x\ln x.\)

Zoezi\(\PageIndex{4}\)

Tathmini\[\lim_{x→0}x\cot x. \nonumber \]

Kidokezo

Andika\(x\cot x=\dfrac{x \cos x}{\sin x}\)

Jibu

\(1\)

Aina ya aina isiyo ya kawaida\(∞−∞\)

Aina nyingine ya fomu indeterminate ni\(∞−∞.\) Fikiria mfano ufuatao. Hebu\(n\) kuwa integer chanya na basi\(f(x)=3x^n\) na\(g(x)=3x^2+5\). Kama\(x→∞, f(x)→∞\) na\(g(x)→∞\). Sisi ni nia ya\(\displaystyle\lim_{x→∞}(f(x)−g(x))\). Kulingana na\(f(x)\) kukua kwa kasi,\(g(x)\) kukua kwa kasi, au hukua kwa kiwango sawa, kama tunavyoona ijayo, chochote kinaweza kutokea katika kikomo hiki. Tangu\(f(x)→∞\) na\(g(x)→∞\), tunaandika\(∞−∞\) ili kuashiria fomu ya kikomo hiki. Kama ilivyo kwa aina zetu nyingine indeterminate,\(∞−∞\) haina maana peke yake na ni lazima kufanya uchambuzi zaidi kuamua thamani ya kikomo. Kwa mfano, tuseme n exponent katika kazi\(f(x)=3x^n\) ni\(n=3\), basi

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^3−3x^2−5)=∞. \nonumber \]

Kwa upande mwingine, kama\(n=2,\) basi

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x^2−3x^2−5)=−5. \nonumber \]

Hata hivyo, kama\(n=1\), basi

\[\lim_{x→∞}(f(x)−g(x))=\lim_{x→∞}(3x−3x^2−5)=−∞. \nonumber \]

Kwa hiyo, kikomo hakiwezi kuamua kwa kuzingatia tu\(∞−∞\). Halafu tunaona jinsi ya kuandika upya maneno yanayohusisha fomu isiyo ya kawaida\(∞−∞\) kama sehemu ya kutumia utawala wa L'Hôpital.

Mfano\(\PageIndex{5}\): Indeterminate Form of Type \(∞−∞\)

Tathmini\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right). \nonumber \]

Suluhisho

Kwa kuchanganya sehemu ndogo, tunaweza kuandika kazi kama quotient. Tangu denominator angalau kawaida ni\(x^2\tan x,\) tuna

\(\dfrac{1}{x^2}−\dfrac{1}{\tan x}=\dfrac{(\tan x)−x^2}{x^2\tan x}\).

Kama\(x→0^+\), nambari\(\tan x−x^2→0\) na denominator\(x^2\tan x→0.\) Kwa hiyo, tunaweza kutumia utawala wa L'Hôpital. Kuchukua derivatives ya nambari na denominator, tuna

\[\lim_{x→0^+}\dfrac{(\tan x)−x^2}{x^2\tan x}=\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}. \nonumber \]

kama\(x→0^+\),\((\sec^2x)−2x→1\) na\(x^2\sec^2x+2x\tan x→0\). Tangu denominator ni chanya kama\(x\) mbinu sifuri kutoka kulia, sisi kuhitimisha kwamba

\[\lim_{x→0^+}\dfrac{(\sec^2x)−2x}{x^2\sec^2x+2x\tan x}=∞. \nonumber \]

Kwa hiyo,

\[\lim_{x→0^+}\left(\dfrac{1}{x^2}−\dfrac{1}{\tan x}\right)=∞. \nonumber \]

Zoezi\(\PageIndex{5}\)

Tathmini\(\displaystyle \lim_{x→0^+}\left(\dfrac{1}{x}−\dfrac{1}{\sin x}\right)\).

Kidokezo

Andika upya tofauti ya sehemu ndogo kama sehemu moja.

Jibu

0

Aina nyingine ya fomu indeterminate ambayo hutokea wakati kutathmini mipaka inahusisha exponents. Maneno\(0^0, ∞^0\), na\(1^∞\) ni aina zote indeterminate. Kwao wenyewe, maneno haya hayana maana kwa sababu hatuwezi kutathmini maneno haya kama tunavyoweza kutathmini usemi unaohusisha namba halisi. Badala yake, maneno haya yanawakilisha fomu zinazotokea wakati wa kupata mipaka. Sasa tunachunguza jinsi utawala wa L'Hôpital unaweza kutumika kutathmini mipaka inayohusisha fomu hizi zisizojulikana.

Kwa kuwa utawala wa L'Hôpital unatumika kwa quotients, tunatumia kazi ya asili ya logarithm na mali zake ili kupunguza tatizo kutathmini kikomo kinachohusisha viongozi na tatizo linalohusiana na kikomo cha quotient. Kwa mfano, tuseme tunataka kutathmini\(\displaystyle \lim_{x→a}f(x)^{g(x)}\) na tunafika kwenye fomu isiyo ya kawaida\(∞^0\). (Aina indeterminate\(0^0\) na\(1^∞\) inaweza kushughulikiwa sawa.) Tunaendelea kama ifuatavyo. Hebu

\[y=f(x)^{g(x)}. \nonumber \]

Kisha,

\[\ln y=\ln(f(x)^{g(x)})=g(x)\ln(f(x)). \nonumber \]

Kwa hiyo,

\[\lim_{x→a}[\ln(y)]=\lim_{x→a}[g(x)\ln(f(x))]. \nonumber \]

Kwa kuwa\(\displaystyle \lim_{x→a}f(x)=∞,\) tunajua kwamba\(\displaystyle \lim_{x→a}\ln(f(x))=∞\). Kwa hiyo,\(\displaystyle \lim_{x→a}g(x)\ln(f(x))\) ni ya fomu indeterminate\(0⋅∞\), na tunaweza kutumia mbinu zilizojadiliwa mapema ili kuandika upya maneno\(g(x)\ln(f(x))\) katika fomu ili tuweze kutumia utawala wa L'Hôpital. Tuseme\(\displaystyle \lim_{x→a}g(x)\ln(f(x))=L\),\(L\) wapi inaweza kuwa\(∞\) au\(−∞.\) Kisha

\[\lim_{x→a}[\ln(y)]=L. \nonumber \]

Kwa kuwa kazi ya asili ya logarithm inaendelea, tunahitimisha kuwa

\[\ln\left(\lim_{x→a}y\right)=L, \nonumber \]

ambayo inatupa

\[\lim_{x→a}y=\lim_{x→a}f(x)^{g(x)}=e^L. \nonumber \]

Mfano\(\PageIndex{6}\): Indeterminate Form of Type \(∞^0\)

Tathmini\[\lim_{x→∞}x^{1/x}. \nonumber \]

Suluhisho

Hebu\(y=x^{1/x}\) .Kisha,

\[\ln(x^{1/x})=\dfrac{1}{x}\ln x=\dfrac{\ln x}{x}. \nonumber \]

Tunahitaji kutathmini\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x}\). Kutumia utawala wa L'Hôpital, tunapata

\[\lim_{x→∞}\ln y=\lim_{x→∞}\dfrac{\ln x}{x}=\lim_{x→∞}\dfrac{1/x}{1}=0. \nonumber \]

Kwa hiyo,\(\displaystyle \lim_{x→∞}\ln y=0.\) Tangu logarithm asili kazi ni kuendelea, sisi kuhitimisha kwamba

\[\ln\left(\lim_{x→∞}y\right)=0, \nonumber \]

ambayo inaongoza kwa

\[\lim_{x→∞}x^{1/x}=\lim_{x→∞}y=e^{\ln\left(\lim_{x→∞}y\right)}=e^0=1. \nonumber \]

Hivyo,

\[\lim_{x→∞}x^{1/x}=1. \nonumber \]

Zoezi\(\PageIndex{6}\)

Tathmini\[\lim_{x→∞}x^{1/\ln(x)}. \nonumber \]

Kidokezo

Hebu\(y=x^{1/\ln(x)}\) na kutumia logarithm ya asili kwa pande zote mbili za equation.

Jibu

\(e\)

Mfano\(\PageIndex{7}\): Indeterminate Form of Type \(0^0\)

Tathmini\[\lim_{x→0^+}x^{\sin x}. \nonumber \]

Suluhisho

Hebu

\[y=x^{\sin x}. \nonumber \]

Kwa hiyo,

\[\ln y=\ln(x^{\sin x})=\sin x\ln x. \nonumber \]

Sasa tathmini\(\displaystyle\lim_{x→0^+}\sin x\ln x.\) Tangu\(\displaystyle\lim_{x→0^+}\sin x=0\) na\(\displaystyle\lim_{x→0^+}\ln x=−∞\), tuna fomu indeterminate\(0⋅∞\). Ili kutumia utawala wa L'Hôpital, tunahitaji kuandika upya\(\sin x\ln x\) kama sehemu. Tunaweza kuandika

\[\sin x\ln x=\dfrac{\sin x}{1/\ln x} \nonumber \]

au

\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x}. \nonumber \]

Hebu fikiria chaguo la kwanza. Katika kesi hiyo, kwa kutumia utawala wa L'Hôpital, tungepata

\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\sin x}{1/\ln x}=\lim_{x→0^+}\dfrac{\cos x}{−1/(x(\ln x)^2)}=\lim_{x→0^+}(−x(\ln x)^2\cos x).\nonumber \]

Kwa bahati mbaya, hatuna tu kujieleza mwingine unaohusisha fomu isiyo ya kawaida\(0⋅∞,\) lakini kikomo kipya ni ngumu zaidi kutathmini kuliko ile ambayo tulianza. Badala yake, tunajaribu chaguo la pili. Kwa kuandika

\[\sin x\ln x=\dfrac{\ln x}{1/\sin x}=\dfrac{\ln x}{\csc x,} \nonumber \]

na kutumia utawala wa L'Hôpital, tunapata

\[\lim_{x→0^+}\sin x\ln x=\lim_{x→0^+}\dfrac{\ln x}{\csc x}=\lim_{x→0^+}\dfrac{1/x}{−\csc x\cot x}=\lim_{x→0^+}\dfrac{−1}{x\csc x\cot x}. \nonumber \]

Kutumia ukweli kwamba\(\csc x=\dfrac{1}{\sin x}\) na\(\cot x=\dfrac{\cos x}{\sin x}\), tunaweza kuandika upya maneno upande wa kulia kama

\[\lim_{x→0^+}\dfrac{−\sin^2x}{x\cos x}=\lim_{x→0^+}\left[\dfrac{\sin x}{x}⋅(−\tan x)\right]=\left(\lim_{x→0^+}\dfrac{\sin x}{x}\right)⋅\left(\lim_{x→0^+}(−\tan x)\right)=1⋅0=0. \nonumber \]

Sisi kuhitimisha kwamba\(\displaystyle\lim_{x→0^+}\ln y=0.\) Kwa hiyo,\(\displaystyle\ln\left(\lim_{x→0^+}y\right)=0\) na sisi

\[\lim_{x→0^+}y=\lim_{x→0^+}x^{\sin x}=e^0=1.\nonumber \]

Hivyo,

\[\lim_{x→0^+}x^{\sin x}=1. \nonumber \]

Zoezi\(\PageIndex{7}\)

Tathmini\(\displaystyle \lim_{x→0^+}x^x\).

Kidokezo

Hebu\(y=x^x\) na uchukue logarithm ya asili ya pande zote mbili za equation.

Jibu

1

Viwango vya ukuaji wa Kazi

Tuseme kazi\(f\) na\(g\) wote mbinu infinity kama\(x→∞\). Ingawa maadili ya kazi zote mbili huwa kubwa kwa kiasi kikubwa kama maadili ya\(x\) kuwa kubwa ya kutosha, wakati mwingine kazi moja inakua kwa haraka zaidi kuliko nyingine. Kwa mfano,\(f(x)=x^2\) na\(g(x)=x^3\) wote mbinu infinity kama\(x→∞\). Hata hivyo, kama\(\PageIndex{1}\) inaonyesha Jedwali, maadili ya\(x^3\) yanaongezeka kwa kasi zaidi kuliko maadili ya\(x^2\).

Jedwali\(\PageIndex{1}\): Kulinganisha Viwango vya Ukuaji wa\(x^2\) na\(x^3\)

\(x\)	10	100	1000	10,000
\(f(x)=x^2\)	100	10,000	1,000,000	100,000,000
\(g(x)=x^3\)	1000	1,000,000	1,000,000,000	1,000,000,000

Kwa kweli,

\[\lim_{x→∞}\dfrac{x^3}{x^2}=\lim_{x→∞}x=∞. \nonumber \]

au, sawa

\[\lim_{x→∞}\dfrac{x^2}{x^3}=\lim_{x→∞}\dfrac{1}{x}=0. \nonumber \]

Matokeo yake, tunasema\(x^3\) ni kukua kwa kasi zaidi kuliko\(x^2\) kama\(x→∞\). Kwa upande mwingine, kwa\(f(x)=x^2\) na\(g(x)=3x^2+4x+1\), ingawa maadili ya daima\(g(x)\) ni kubwa kuliko maadili ya\(f(x)\) kwa\(x>0\), kila thamani ya\(g(x)\) ni takribani mara tatu thamani sambamba ya\(f(x)\) kama\(x→∞\), kama inavyoonekana katika Jedwali\(\PageIndex{2}\). Kwa kweli,

\[\lim_{x→∞}\dfrac{x^2}{3x^2+4x+1}=\dfrac{1}{3}. \nonumber \]

Jedwali\(\PageIndex{2}\): Kulinganisha Viwango vya Ukuaji wa\(x^2\) na\(3x^2+4x+1\)

\(x\)	10	100	1000	10,000
\(f(x)=x^2\)	100	10,000	1,000,000	100,000,000
\(g(x)=3x^2+4x+1\)	341	30,401	3,004,001	300,040,001

Katika kesi hiyo, tunasema kwamba\(x^2\) na\(3x^2+4x+1\) ni kuongezeka kwa kiwango sawa na\(x→∞.\)

Kwa ujumla zaidi, tuseme\(f\) na\(g\) ni kazi mbili ambazo mbinu infinity kama\(x→∞\). Tunasema\(g\) kukua kwa kasi zaidi kuliko\(f\)\(x→∞\) kama

\[\lim_{x→∞}\dfrac{g(x)}{f(x)}=∞ \quad \text{or, equivalently,} \quad \lim_{x→∞}\dfrac{f(x)}{g(x)}=0. \nonumber \]

Kwa upande mwingine, kama kuna mara kwa mara\(M≠0\) vile

\[\lim_{x→∞}\dfrac{f(x)}{g(x)}=M, \nonumber \]

tunasema\(f\) na\(g\) kukua kwa kiwango sawa na\(x→∞\).

Halafu tunaona jinsi ya kutumia utawala wa L'Hôpital kulinganisha viwango vya ukuaji wa nguvu, ufafanuzi, na kazi za logarithmic.

Mfano\(\PageIndex{8}\): Comparing the Growth Rates of \(\ln(x)\), \(x^2\), and \(e^x\)

Kwa kila moja ya jozi zifuatazo za kazi, tumia utawala wa L'Hôpital kutathmini\[\lim_{x→∞}\dfrac{f(x)}{g(x)}. \nonumber \]

1. \(f(x)=x^2\)na\(g(x)=e^x\)
2. \(f(x)=\ln(x)\)na\(g(x)=x^2\)

Suluhisho

a. tangu\(\displaystyle \lim_{x→∞}x^2=∞\) na\(\displaystyle \lim_{x→∞}e^x=∞\), tunaweza kutumia utawala wa L'Hôpital kutathmini\(\displaystyle \lim_{x→∞}\left[\dfrac{x^2}{e^x}\right]\). Tunapata

\[\lim_{x→∞}\frac{x^2}{e^x}=\lim_{x→∞}\frac{2x}{e^x}. \nonumber \]

Tangu\(\displaystyle \lim_{x→∞}2x=∞\) na\(\displaystyle \lim_{x→∞}e^x=∞\), tunaweza kutumia utawala wa L'Hôpital tena. Tangu

\[\lim_{x→∞}\frac{2x}{e^x}=\lim_{x→∞}\frac{2}{e^x}=0, \nonumber \]

tunahitimisha kwamba

\[\lim_{x→∞}\dfrac{x^2}{e^x}=0. \nonumber \]

Kwa hiyo,\(e^x\) kukua kwa kasi zaidi kuliko\(x^2\) kama\(x→∞\) (Angalia Kielelezo\(\PageIndex{3}\) na Jedwali\(\PageIndex{3}\))

Kielelezo\(\PageIndex{3}\): Kazi ya kielelezo inakua kwa kiwango cha kasi zaidi kuliko kazi ya nguvu.

Jedwali\(\PageIndex{3}\): Viwango vya ukuaji wa kazi ya nguvu na kazi ya kielelezo.

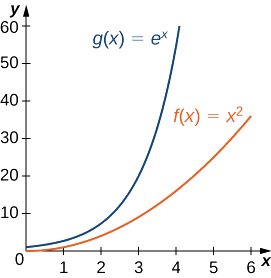
\(x\)	5	10	15	20
\(x^2\)	25	100	225	400
\(e^x\)	148	22,026	3,269,017	485,165,195

b Tangu\(\displaystyle \lim_{x→∞}\ln x=∞\) na\(\displaystyle \lim_{x→∞}x^2=∞\), tunaweza kutumia utawala wa L'Hôpital kutathmini\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{x^2}\). Tunapata

\[\lim_{x→∞}\dfrac{\ln x}{x^2}=\lim_{x→∞}\dfrac{1/x}{2x}=\lim_{x→∞}\dfrac{1}{2x^2}=0. \nonumber \]

Hivyo,\(x^2\) inakua kwa kasi zaidi kuliko\(\ln x\) kama\(x→∞\) (angalia Kielelezo\(\PageIndex{4}\) na Jedwali\(\PageIndex{4}\)).

Kielelezo\(\PageIndex{4}\): Kazi ya nguvu inakua kwa kiwango cha kasi zaidi kuliko kazi ya logarithmic.

Jedwali\(\PageIndex{4}\): Viwango vya ukuaji wa kazi ya nguvu na kazi ya logarithmic

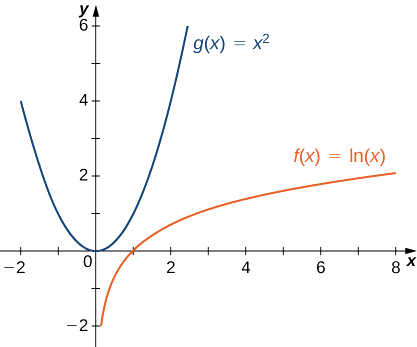
\(x\)	10	100	1000	10,000
\(\ln(x)\)	2.303	4.605	6.908	9.210
\(x^2\)	100	10,000	1,000,000	100,000,000

Zoezi\(\PageIndex{8}\)

Kulinganisha viwango vya ukuaji wa\(x^{100}\) na\(2^x\).

Kidokezo

Tumia utawala wa L'Hôpital kwa\(x^{100}/2^x\).

Jibu

Kazi\(2^x\) inakua kwa kasi zaidi kuliko\(x^{100}\).

Kutumia mawazo sawa na katika\(\PageIndex{8}a\) Mfano. si vigumu kuonyesha kwamba\(e^x\) inakua\(x^p\) kwa kasi zaidi kuliko yoyote\(p>0\). Katika Kielelezo\(\PageIndex{5}\) na Jedwali\(\PageIndex{5}\),\(e^x\) tunalinganisha\(x^3\) na\(x^4\) kama\(x→∞\).

Kielelezo\(\PageIndex{5}\): Kazi ya kielelezo\(e^x\) inakua\(x^p\) kwa kasi zaidi kuliko yoyote\(p>0\). (a) kulinganisha\(e^x\) na\(x^3\). (b) kulinganisha\(e^x\) na\(x^4\).

Jedwali\(\PageIndex{5}\): Kazi ya kielelezo inakua kwa kiwango cha kasi zaidi kuliko kazi yoyote ya nguvu

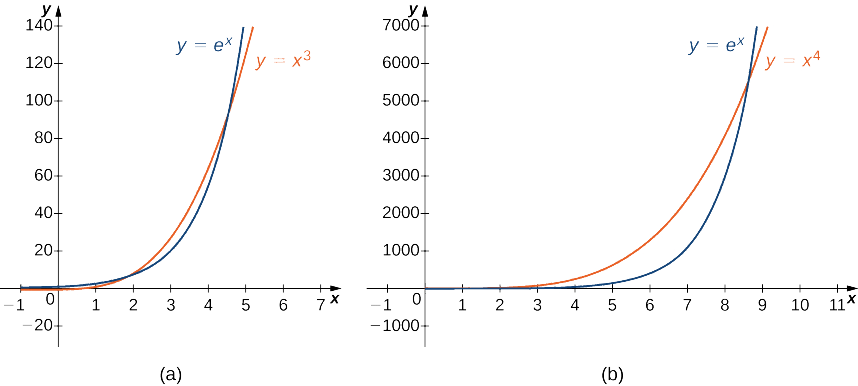
\(x\)	5	10	15	20
\(x^3\)	125	1000	3375	8000
\(x^4\)	625	10,000	50,625	160,000
\(e^x\)	148	22,026	3,269,017	485,165,195

Vile vile, si vigumu kuonyesha kwamba\(x^p\) inakua\(\ln x\) kwa kasi zaidi kuliko yoyote\(p>0\). Katika Kielelezo\(\PageIndex{6}\) na Jedwali\(\PageIndex{6}\),\(\ln x\) tunalinganisha\(\sqrt[3]{x}\) na\(\sqrt{x}\).

Kielelezo\(\PageIndex{6}\): Kazi\(y=\ln(x)\) inakua polepole zaidi kuliko\(x^p\) yoyote\(p>0\) kama\(x→∞\).

Jedwali\(\PageIndex{6}\): Kazi ya logarithmic inakua kwa kiwango cha polepole kuliko kazi yoyote ya mizizi

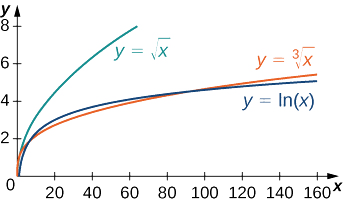
\(x\)	10	100	1000	10,000
\(\ln(x)\)	2.303	4.605	6.908	9.210
\(\sqrt[3]{x}\)	2.154	4.642	10	21.544
\(\sqrt{x}\)	3.162	10	31.623	100

Dhana muhimu

• Utawala wa L'Hôpital unaweza kutumika kutathmini kikomo cha quotient wakati fomu indeterminate\(\dfrac{0}{0}\) au\(∞/∞\) inatokea.
• Utawala wa L'Hôpital pia unaweza kutumika kwa fomu zingine zisizojulikana ikiwa zinaweza kuandikwa upya kwa suala la kikomo kinachohusisha quotient ambayo ina fomu isiyo ya kawaida\(\dfrac{0}{0}\) au\(∞/∞.\)
• Kazi ya kielelezo\(e^x\) inakua kwa kasi zaidi kuliko kazi yoyote ya nguvu\(x^p, p>0\).
• Kazi ya logarithmic\(\ln x\) inakua polepole zaidi kuliko kazi yoyote ya nguvu\(x^p, p>0\).

faharasa

aina zisizotambulika

Wakati kutathmini kikomo, fomu\(\dfrac{0}{0}\)\(∞/∞, 0⋅∞, ∞−∞, 0^0, ∞^0\), na\(1^∞\) ni kuchukuliwa indeterminate kwa sababu uchambuzi zaidi inahitajika kuamua kama kikomo ipo na, kama ni hivyo, thamani yake ni nini.

Utawala wa L'Hôpital

Kama\(f\) na\(g\) ni differentiable kazi juu ya muda\(a\)\(a\), ila uwezekano katika,\(\displaystyle \lim_{x→a}f(x)\) na\(\displaystyle \lim_{x→a}f(x)=0=\lim_{x→a}g(x)\) au na\(\displaystyle \lim_{x→a}g(x)\) ni usio\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}=\lim_{x→a}\dfrac{f′(x)}{g′(x)}\), basi, kuchukua kikomo juu ya haki ipo au ni\(∞\) au\(−∞\).