3.7: Derivatives ya Kazi Inverse
- Page ID
- 178893
- Tumia derivative ya kazi inverse.
- Tambua derivatives ya kazi za kawaida za trigonometric.
Katika sehemu hii sisi kuchunguza uhusiano kati ya derivative ya kazi na derivative ya inverse yake. Kwa kazi ambazo derivatives tunajua tayari, tunaweza kutumia uhusiano huu kupata derivatives ya inverses bila kutumia ufafanuzi wa kikomo wa derivative. Hasa, tutatumia fomu ya derivatives ya kazi za inverse kwa kazi za trigonometric. Fomula hii pia inaweza kutumika kupanua utawala nguvu kwa exponents busara.
Derivative ya Kazi Inverse
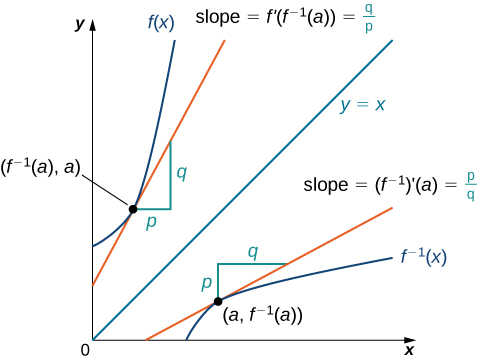
Tunaanza kwa kuzingatia kazi na inverse yake. Kama\(f(x)\) ni wote invertible na kutofautisha, inaonekana busara kwamba inverse\(f(x)\) ya pia kutofautisha. Kielelezo\(\PageIndex{1}\) kinaonyesha uhusiano kati ya kazi\(f(x)\) na inverse yake\(f^{−1}(x)\). Angalia hatua\(\left(a,\,f^{−1}(a)\right)\) kwenye grafu ya\(f^{−1}(x)\) kuwa na mstari wa tangent na mteremko wa
\[\big(f^{−1}\big)′(a)=\dfrac{p}{q}. \nonumber \]
Hatua hii inalingana na hatua\(\left(f^{−1}(a),\,a\right)\) kwenye grafu ya\(f(x)\) kuwa na mstari wa tangent na mteremko wa
\[f′\big(f^{−1}(a)\big)=\dfrac{q}{p}. \nonumber \]
Hivyo, kama\(f^{−1}(x)\) ni differentiable katika\(a\), basi ni lazima kesi kwamba
\(\big(f^{−1}\big)′(a)=\dfrac{1}{f′\big(f^{−1}(a)\big)}\).
Tunaweza pia hupata formula kwa derivative ya inverse kwa kukumbuka kwanza kwamba\(x=f\big(f^{−1}(x)\big)\). Kisha kwa kutofautisha pande zote mbili za equation hii (kwa kutumia utawala wa mnyororo upande wa kulia), tunapata
\(1=f′\big(f^{−1}(x)\big)\big(f^{−1}\big)′(x))\).
Kutatua kwa\(\big(f^{−1}\big)′(x)\), tunapata
\(\big(f^{−1}\big)′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}\).
Sisi muhtasari matokeo haya katika theorem ifuatayo.
Hebu\(f(x)\) kuwa kazi ambayo ni invertible na kutofautishwa. Hebu\(y=f^{−1}(x)\) kuwa inverse ya\(f(x)\). Kwa wote\(x\) kuridhisha\(f′\big(f^{−1}(x)\big)≠0\),
\[\dfrac{dy}{dx}=\dfrac{d}{dx}\big(f^{−1}(x)\big)=\big(f^{−1}\big)′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}.\label{inverse1} \]
Vinginevyo, ikiwa\(y=g(x)\) ni kinyume cha\(f(x)\), basi
\[g'(x)=\dfrac{1}{f′\big(g(x)\big)}. \label{inverse2} \]
Matumizi inverse kazi theorem kupata derivative ya\(g(x)=\dfrac{x+2}{x}\). Linganisha derivative kusababisha na kwamba kupatikana kwa kutofautisha kazi moja kwa moja.
Suluhisho
Inverse ya\(g(x)=\dfrac{x+2}{x}\) ni\(f(x)=\dfrac{2}{x−1}\).
Tutatumia Equation\ ref {inverse2} na kuanza kwa kutafuta\(f′(x)\). Hivyo,
\[f′(x)=\dfrac{−2}{(x−1)^2} \nonumber \]
na
\[f′\big(g(x)\big)=\dfrac{−2}{(g(x)−1)^2}=\dfrac{−2}{\left(\dfrac{x+2}{x}−1\right)^2}=−\dfrac{x^2}{2}. \nonumber \]
Hatimaye,
\[g′(x)=\dfrac{1}{f′\big(g(x)\big)}=−\dfrac{2}{x^2}. \nonumber \]
Tunaweza kuthibitisha kwamba hii ni derivative sahihi kwa kutumia utawala quotient\(g(x)\) ili kupata
\[g′(x)=−\dfrac{2}{x^2}. \nonumber \]
Matumizi inverse kazi theorem kupata derivative ya\(g(x)=\dfrac{1}{x+2}\). Linganisha matokeo yaliyopatikana kwa kutofautisha\(g(x)\) moja kwa moja.
- Kidokezo
-
Tumia mfano uliotangulia kama mwongozo.
- Jibu
-
\(g′(x)=−\dfrac{1}{(x+2)^2}\)
Matumizi inverse kazi theorem kupata derivative ya\(g(x)=\sqrt[3]{x}\).
Suluhisho
Kazi\(g(x)=\sqrt[3]{x}\) ni inverse ya kazi\(f(x)=x^3\). Tangu\(g′(x)=\dfrac{1}{f′\big(g(x)\big)}\), kuanza kwa kutafuta\(f′(x)\). Hivyo,
\[f′(x)=3x^2\nonumber \]
na
\[f′\big(g(x)\big)=3\big(\sqrt[3]{x}\big)^2=3x^{2/3}\nonumber \]
Hatimaye,
\[g′(x)=\dfrac{1}{3x^{2/3}}.\nonumber \]
Kama tungekuwa na kutofautisha\(g(x)\) moja kwa moja, kwa kutumia utawala wa nguvu, tutakuwa kwanza kuandika upya\(g(x)=\sqrt[3]{x}\) kama nguvu ya\(x\) kupata,
\[g(x) = x^{1/3}\nonumber \]
Basi tunataka kutofautisha kutumia utawala nguvu ya kupata
\[g'(x) =\tfrac{1}{3}x^{−2/3} = \dfrac{1}{3x^{2/3}}.\nonumber \]
Kupata derivative ya\(g(x)=\sqrt[5]{x}\) kwa kutumia inverse kazi theorem.
- Kidokezo
-
\(g(x)\)ni kinyume cha\(f(x)=x^5\).
- Jibu
-
\(g(x)=\frac{1}{5}x^{−4/5}\)
Kutoka mfano uliopita, tunaona kwamba tunaweza kutumia inverse kazi theorem kupanua utawala nguvu kwa exponents ya fomu\(\dfrac{1}{n}\), ambapo\(n\) ni integer chanya. Ugani huu hatimaye utatuwezesha kutofautisha\(x^q\), wapi\(q\) nambari yoyote ya busara.
Utawala wa nguvu unaweza kupanuliwa kwa watazamaji wa busara. Hiyo ni, ikiwa\(n\) ni integer chanya, basi
\[\dfrac{d}{dx}\big(x^{1/n}\big)=\dfrac{1}{n} x^{(1/n)−1}. \nonumber \]
Pia, ikiwa\(n\) ni integer chanya na\(m\) ni integer ya kiholela, basi
\[\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{m}{n}x^{(m/n)−1}. \nonumber \]
Kazi\(g(x)=x^{1/n}\) ni inverse ya kazi\(f(x)=x^n\). Tangu\(g′(x)=\dfrac{1}{f′\big(g(x)\big)}\), kuanza kwa kutafuta\(f′(x)\). Hivyo,
\(f′(x)=nx^{n−1}\)na\(f′\big(g(x)\big)=n\big(x^{1/n}\big)^{n−1}=nx^{(n−1)/n}\).
Hatimaye,
\(g′(x)=\dfrac{1}{nx^{(n−1)/n}}=\dfrac{1}{n}x^{(1−n)/n}=\dfrac{1}{n}x^{(1/n)−1}\).
Ili kutofautisha\(x^{m/n}\) tunapaswa kuandika upya kama\((x^{1/n})^m\) na kutumia utawala wa mnyororo. Hivyo,
\[\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{d}{dx}\big((x^{1/n}\big)^m)=m\big(x^{1/n}\big)^{m−1}⋅\dfrac{1}{n}x^{(1/n)−1}=\dfrac{m}{n}x^{(m/n)−1}. \nonumber \]
□
Kupata equation ya tangent line kwa grafu ya\(y=x^{2/3}\) saa\(x=8\).
Suluhisho
Kwanza kupata\(\dfrac{dy}{dx}\) na kutathmini katika\(x=8\). Tangu
\[\dfrac{dy}{dx}=\frac{2}{3}x^{−1/3} \nonumber \]
na
\[\dfrac{dy}{dx}\Bigg|_{x=8}=\frac{1}{3}\nonumber \]
mteremko wa mstari wa tangent kwenye grafu\(x=8\) ni\(\frac{1}{3}\).
\(x=8\)Kubadilisha kazi ya awali, tunapata\(y=4\). Hivyo, mstari wa tangent hupita kupitia hatua\((8,4)\). Kubadilisha fomu ya mteremko wa uhakika kwa mstari, tunapata mstari wa tangent
\[y=\tfrac{1}{3}x+\tfrac{4}{3}. \nonumber \]
Kupata derivative ya\(s(t)=\sqrt{2t+1}\).
- Kidokezo
-
Tumia utawala wa mnyororo.
- Jibu
-
\(s′(t)=(2t+1)^{−1/2}\)
Derivatives ya Inverse Trigonometric
Sasa tunageuka mawazo yetu kutafuta derivatives ya kazi inverse trigonometric. Derivatives hizi zitathibitisha kuwa muhimu katika utafiti wa ushirikiano baadaye katika maandiko haya. Vipindi vya kazi za trigonometric inverse ni ajabu sana kwa kuwa derivatives yao ni kweli kazi za algebraic. Hapo awali, derivatives ya kazi za algebraic imethibitishwa kuwa kazi za algebraic na derivatives ya kazi za trigonometric zimeonyeshwa kuwa kazi za trigonometric. Hapa, kwa mara ya kwanza, tunaona kwamba derivative ya kazi haipaswi kuwa ya aina moja kama kazi ya awali.
Matumizi inverse kazi theorem kupata derivative ya\(g(x)=\sin^{−1}x\).
Suluhisho
Tangu\(x\) kwa muda\(\left[−\frac{π}{2},\frac{π}{2}\right],f(x)=\sin x\) ni inverse ya\(g(x)=\sin^{−1}x\), kuanza kwa kutafuta\(f′(x)\). Tangu
\[f′(x)=\cos x \nonumber \]
na
\[f′\big(g(x)\big)=\cos \big( \sin^{−1}x\big)=\sqrt{1−x^2} \nonumber \]
tunaona kwamba
\[g′(x)=\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{f′\big(g(x)\big)}=\dfrac{1}{\sqrt{1−x^2}} \nonumber \]
Uchambuzi
Ili kuona kwamba\(\cos(\sin^{−1}x)=\sqrt{1−x^2}\), fikiria hoja ifuatayo. Weka\(\sin^{−1}x=θ\). Katika kesi hii,\(\sin θ=x\) wapi\(−\frac{π}{2}≤θ≤\frac{π}{2}\). Tunaanza kwa kuzingatia kesi ambapo\(0<θ<\frac{π}{2}\). Kwa kuwa\(θ\) ni angle papo hapo, tunaweza kujenga pembetatu haki kuwa angle papo hapo\(θ\), hypotenuse ya urefu\(1\) na upande kinyume angle\(θ\) kuwa urefu\(x\). Kutoka theorem ya Pythagorean, upande wa karibu na angle\(θ\) una urefu\(\sqrt{1−x^2}\). Pembetatu hii inavyoonekana kwenye Kielelezo\(\PageIndex{2}\) Kutumia pembetatu, tunaona hiyo\(\cos(\sin^{−1}x)=\cos θ=\sqrt{1−x^2}\).
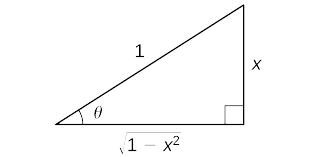
Katika kesi ambapo\(−\frac{π}{2}<θ<0\), sisi kufanya uchunguzi kwamba\(0<−θ<\frac{π}{2}\) na hivyo
\(\cos\big(\sin^{−1}x\big)=\cos θ=\cos(−θ)=\sqrt{1−x^2}\).
Sasa kama\(θ=\frac{π}{2}\)\(θ=−\frac{π}{2},x=1\) au\(x=−1\), na kwa kuwa katika hali yoyote\(\cosθ=0\) na\(\sqrt{1−x^2}=0\), tuna
\(\cos\big(\sin^{−1}x\big)=\cosθ=\sqrt{1−x^2}\).
Kwa hiyo, katika hali zote,
\[\cos\big(\sin^{−1}x\big)=\sqrt{1−x^2}.\nonumber \]
Tumia utawala mnyororo kwa formula inayotokana katika Mfano\(\PageIndex{4A}\) kupata derivative ya\(h(x)=\sin^{−1}\big(g(x)\big)\) na kutumia matokeo haya ili kupata derivative ya\(h(x)=\sin^{−1}(2x^3).\)
Suluhisho
Kutumia utawala mnyororo kwa\(h(x)=\sin^{−1}\big(g(x)\big)\), tuna
\(h′(x)=\dfrac{1}{\sqrt{1−\big(g(x)\big)^2}}g′(x)\).
Sasa basi\(g(x)=2x^3,\) hivyo\(g′(x)=6x^2\). Kubadilisha matokeo ya awali, tunapata
\(\begin{align*} h′(x)&=\dfrac{1}{\sqrt{1−4x^6}}⋅6x^2\\[4pt]&=\dfrac{6x^2}{\sqrt{1−4x^6}}\end{align*}\)
Matumizi inverse kazi theorem kupata derivative ya\(g(x)=\tan^{−1}x\).
- Kidokezo
-
Inverse ya\(g(x)\) ni\(f(x)=\tan x\). Tumia Mfano\(\PageIndex{4A}\) kama mwongozo.
- Jibu
-
\(g′(x)=\dfrac{1}{1+x^2}\)
Vipengee vya kazi zilizobaki za trigonometric zinaweza pia kupatikana kwa kutumia theorem ya kazi ya inverse. Njia hizi hutolewa katika theorem ifuatayo.
\[\begin{align} \dfrac{d}{dx}\big(\sin^{−1}x\big) &=\dfrac{1}{\sqrt{1−x^2}} \label{trig1} \\[4pt] \dfrac{d}{dx}\big(\cos^{−1}x\big) &=\dfrac{−1}{\sqrt{1−x^2}} \label{trig2} \\[4pt] \dfrac{d}{dx}\big(\tan^{−1}x\big) &=\dfrac{1}{1+x^2} \label{trig3} \\[4pt] \dfrac{d}{dx}\big(\cot^{−1}x\big) &=\dfrac{−1}{1+x^2} \label{trig4} \\[4pt] \dfrac{d}{dx}\big(\sec^{−1}x\big) &=\dfrac{1}{|x|\sqrt{x^2−1}} \label{trig5} \\[4pt] \dfrac{d}{dx}\big(\csc^{−1}x\big) &=\dfrac{−1}{|x|\sqrt{x^2−1}} \label{trig6} \end{align} \]
Kupata derivative ya\(f(x)=\tan^{−1}(x^2).\)
Suluhisho
Hebu\(g(x)=x^2\), hivyo\(g′(x)=2x\). Kubadilisha katika Equation\ ref {trig3}, tunapata
\(f′(x)=\dfrac{1}{1+(x^2)^2}⋅(2x).\)
Kurahisisha, tuna
\(f′(x)=\dfrac{2x}{1+x^4}\).
Kupata derivative ya\(h(x)=x^2 \sin^{−1}x.\)
Suluhisho
Kwa kutumia utawala wa bidhaa, tuna
\(h′(x)=2x\sin^{−1}x+\dfrac{1}{\sqrt{1−x^2}}⋅x^2\)
Kupata derivative ya\(h(x)=\cos^{−1}(3x−1).\)
- Kidokezo
-
Matumizi Equation\ ref {trig2}. kwa\(g(x)=3x−1\)
- Jibu
-
\(h′(x)=\dfrac{−3}{\sqrt{6x−9x^2}}\)
Msimamo wa chembe kwa wakati\(t\) hutolewa na\(s(t)=\tan^{−1}\left(\frac{1}{t}\right)\) kwa\(t≥ \ce{1/2}\). Pata kasi ya chembe kwa wakati\( t=1\).
Suluhisho
Anza kwa\(s(t)\) kutofautisha ili kupata\(v(t)\) .Hivyo,
\(v(t)=s′(t)=\dfrac{1}{1+\left(\frac{1}{t}\right)^2}⋅\dfrac{−1}{t^2}\).
Kurahisisha, tuna
\(v(t)=−\dfrac{1}{t^2+1}\).
Hivyo,\(v(1)=−\dfrac{1}{2}.\)
Kupata equation ya tangent line kwa grafu ya\(f(x)=\sin^{−1}x\) saa\(x=0.\)
- Kidokezo
-
\(f′(0)\)ni mteremko wa mstari wa tangent.
- Jibu
-
\(y=x\)
Dhana muhimu
- Theorem ya kazi ya inverse inatuwezesha kuhesabu derivatives ya kazi za inverse bila kutumia ufafanuzi wa kikomo wa derivative.
- Tunaweza kutumia theorem ya kazi inverse kuendeleza formula tofauti kwa kazi inverse trigonometric.
Mlinganyo muhimu
- Theorem ya kazi ya kinyume
\((f^{−1})′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}\)wakati wowote\(f′\big(f^{−1}(x)\big)≠0\) na\(f(x)\) ni differentiable.
- Utawala wa nguvu na watazamaji wa busara
\(\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{m}{n}x^{(m/n)−1}.\)
- Derivative ya inverse sine kazi
\(\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{\sqrt{1−x^2}}\)
- Derivative ya kazi inverse cosine
\(\dfrac{d}{dx}\big(\cos^{−1}x\big)=\dfrac{−1}{\sqrt{1−x^2}}\)
Derivative ya kazi inverse tangent
\(\dfrac{d}{dx}\big(\tan^{−1}x\big)=\dfrac{1}{1+x^2}\)
Derivative ya kazi inverse cotangent
\(\dfrac{d}{dx}\big(\cot^{−1}x\big)=\dfrac{−1}{1+x^2}\)
Derivative ya inverse secant kazi
\(\dfrac{d}{dx}\big(\sec^{−1}x\big)=\dfrac{1}{|x|\sqrt{x^2−1}}\)
Derivative ya kazi inverse cosecant
\(\dfrac{d}{dx}\big(\csc^{−1}x\big)=\dfrac{−1}{|x|\sqrt{x^2−1}}\)
Wachangiaji na Majina
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College) added the second half of Example \(\PageIndex{2}\).


