3.5: Derivatives ya Kazi za Trigonometri
- Page ID
- 178897
- Pata derivatives ya kazi ya sine na cosine.
- Pata derivatives ya kazi za kawaida za trigonometric.
- Tumia derivatives ya juu ya sine na cosine.
Moja ya aina muhimu zaidi ya mwendo katika fizikia ni rahisi harmonic mwendo, ambayo ni kuhusishwa na mifumo kama vile kitu na wingi oscillating juu ya spring. Mwendo rahisi wa harmonic unaweza kuelezewa kwa kutumia kazi za sine au cosine. Katika sehemu hii sisi kupanua ujuzi wetu wa formula derivative ni pamoja na derivatives ya kazi hizi na nyingine trigonometric. Tunaanza na derivatives ya kazi za sine na cosine na kisha tuitumie ili kupata fomu kwa ajili ya derivatives ya kazi nne zilizobaki za trigonometric. Kuwa na uwezo wa kuhesabu derivatives ya kazi za sine na cosine zitatuwezesha kupata kasi na kasi ya mwendo rahisi wa harmonic.
Derivatives ya Kazi za Sine na Cosine
Tunaanza utafutaji wetu wa derivative kwa kazi sine kwa kutumia formula kufanya nadhani busara katika derivative yake. Kumbuka kwamba kwa ajili ya kazi\(f(x),\)
\[f′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
Kwa hiyo, kwa maadili ya karibu\(h\) sana\(0\),
\[f′(x)≈\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
Tunaona kwamba kwa kutumia\(h=0.01\),
\[\dfrac{d}{dx}(\sin x)≈\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]
Kwa kuweka
\[D(x)=\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]
na kutumia matumizi ya graphing, tunaweza kupata grafu ya makadirio ya derivative ya\(\sin x\) (Kielelezo\(\PageIndex{1}\)).
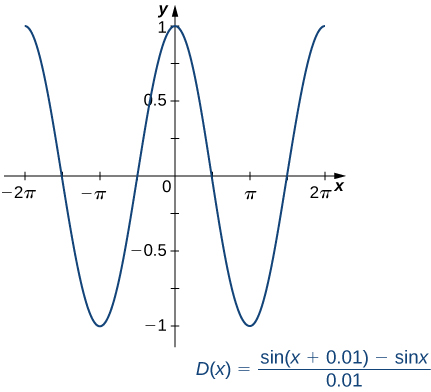
Baada ya ukaguzi, grafu ya\(D(x)\) inaonekana kuwa karibu sana na grafu ya kazi ya cosine. Hakika, tutaonyesha kwamba
\[\dfrac{d}{dx}(\sin x)=\cos x. \nonumber \]
Ikiwa tungefuata hatua sawa na takriban derivative ya kazi ya cosine, tungependa kupata hiyo
\[\dfrac{d}{dx}(\cos x)=−\sin x. \nonumber \]
Mchanganyiko wa kazi ya sine ni cosine na derivative ya kazi ya cosine ni sine hasi.
\[\dfrac{d}{dx}(\sin x)=\cos x \nonumber \]
\[\dfrac{d}{dx}(\cos x)=−\sin x \nonumber \]
Kwa sababu ushahidi kwa\(\dfrac{d}{dx}(\sin x)=\cos x\) na\(\dfrac{d}{dx}(\cos x)=−\sin x\) kutumia mbinu sawa, sisi kutoa tu ushahidi kwa\(\dfrac{d}{dx}(\sin x)=\cos x\). Kabla ya mwanzo, kumbuka mipaka miwili muhimu ya trigonometric:
\(\displaystyle \lim_{h→0}\dfrac{\sin h}{h}=1\)na\(\displaystyle \lim_{h→0}\dfrac{\cos h−1}{h}=0\).
Grafu za\(y=\dfrac{\sin h}{h}\) na\(y=\dfrac{\cos h−1}{h}\) zinaonyeshwa kwenye Kielelezo\(\PageIndex{2}\).
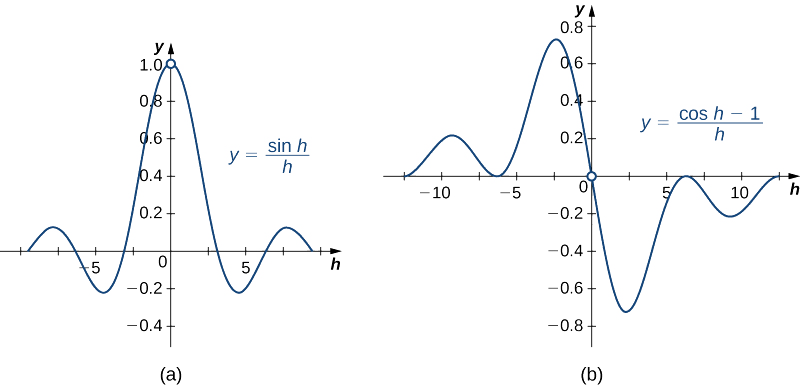
Tunakumbuka pia utambulisho wafuatayo wa trigonometric kwa sine ya jumla ya pembe mbili:
\[\sin (x+h)=\sin x\cos h+\cos x\sin h. \nonumber \]
Sasa kwa kuwa tumekusanya equations zote muhimu na utambulisho, tunaendelea na ushahidi.
\ [kuanza {align*}\ dfrac {d} {dx} (\ dhambi x) &=\ lim_ {h → 0}\ dfrac {\ dhambi (x+h) -\ dhambi x} {h} & &\ maandishi {Tumia ufafanuzi wa derivative.}\\ [4pt]
&=\ lim_ {h → 0}\ dfrac {\ dhambi x\ cos h+\ cos x\ dhambi h-\ dhambi x} {h} & &\ maandishi {Tumia utambulisho wa trig kwa sine ya jumla ya pembe mbili.}\\ [4pt]
&=\ lim_ {h → 0}\ kushoto (\ dfrac {\ dhambi x\ cos h-\ dhambi x} {h} +\ dfrac {\ cos x\ dhambi h} {h}\ haki) & &\ maandishi {Kuunganisha tena.}\\ [4pt]
&=\ lim_ {h→ 0}\ kushoto (\ dhambi x\ kushoto (\ dfrac {\ cos h-1 1} {h}\ haki) + (\ cos x)\ kushoto (\ dfrac {\ dhambi h} {h}\ haki)\ haki) & &\ maandishi {Factor nje}\ dhambi x\ maandishi {na}\ cos x\\ [4pt]
& =(\ dhambi x)\ lim_ {h→ 0}\ kushoto (\ dfrac {\ cos h-1} {h}\ haki) + (\ cos x)\ lim_ {h → 0}\ kushoto (\ dfrac {\ dhambi h} {h}\ haki) & &\ maandishi {Factor}\ dhambi x\ maandishi {na}\ cos x\ maandishi {nje ya mipaka.}\\ [4pt]
& =(\ dhambi x) (0) + (\ cos x) (1) & &\ maandishi {Weka trig kikomo formula.}\\ [4pt]
&=\ cos x & &\ maandishi {Kurahisisha.} \ mwisho {align*}\ nonumber\]
□
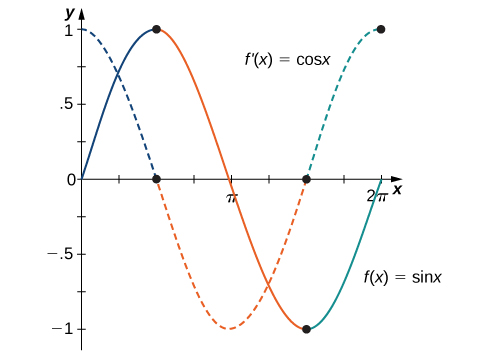
Kielelezo\(\PageIndex{3}\) inaonyesha uhusiano kati ya grafu ya\(f(x)=\sin x\) na derivative yake\(f′(x)=\cos x\). Angalia kwamba katika maeneo ambayo\(f(x)=\sin x\) ina tangent ya usawa, derivative yake\(f′(x)=\cos x\) inachukua thamani sifuri. Pia tunaona kwamba ambapo f\((x)=\sin x\) ni kuongezeka,\(f′(x)=\cos x>0\) na wapi\(f(x)=\sin x\) ni kupungua,\(f′(x)=\cos x<0.\)
Kupata derivative ya\(f(x)=5x^3\sin x\).
Suluhisho
Kutumia utawala wa bidhaa, tuna
\[ \begin{align*} f'(x) &=\dfrac{d}{dx}(5x^3)⋅\sin x+\dfrac{d}{dx}(\sin x)⋅5x^3 \\[4pt] &=15x^2⋅\sin x+\cos x⋅5x^3. \end{align*}\]
Baada ya kurahisisha, tunapata
\[f′(x)=15x^2\sin x+5x^3\cos x. \nonumber \]
Kupata derivative ya\(f(x)=\sin x\cos x.\)
- Kidokezo
-
Usisahau kutumia utawala wa bidhaa.
- Jibu
-
\[f′(x)=\cos^2x−\sin^2x \nonumber \]
Kupata derivative ya\(g(x)=\dfrac{\cos x}{4x^2}\).
Suluhisho
Kwa kutumia utawala quotient, tuna
\[g′(x)=\dfrac{(−\sin x)4x^2−8x(\cos x)}{(4x^2)^2}. \nonumber \]
Kurahisisha, sisi kupata
\[g′(x)=\dfrac{−4x^2\sin x−8x\cos x}{16x^4}=\dfrac{−x\sin x−2\cos x}{4x^3}. \nonumber \]
Kupata derivative ya\(f(x)=\dfrac{x}{\cos x}\).
- Kidokezo
-
Tumia utawala wa quotient.
- Jibu
-
\(f'(x) = \dfrac{\cos x+x\sin x}{\cos^2x}\)
Chembe huenda kando ya mhimili wa kuratibu kwa namna ambayo msimamo wake kwa wakati\(t\) unatolewa na\(s(t)=2\sin t−t\) kwa\(0≤t≤2π.\) Kwa nyakati gani chembe hupumzika?
Suluhisho
Kuamua wakati chembe ni katika mapumziko, kuweka\(s′(t)=v(t)=0.\) Anza kwa kutafuta\(s′(t).\) Sisi kupata
\[s′(t)=2 \cos t−1, \nonumber \]
hivyo ni lazima kutatua
\[2 \cos t−1=0\text{ for }0≤t≤2π. \nonumber \]
Ufumbuzi wa equation hii ni\(t=\dfrac{π}{3}\) na\(t=\dfrac{5π}{3}\). Hivyo chembe inapumzika mara kwa mara\(t=\dfrac{π}{3}\) na\(t=\dfrac{5π}{3}\).
Chembe inakwenda pamoja na mhimili wa kuratibu. Msimamo wake kwa wakati\(t\) hutolewa na kwa\(s(t)=\sqrt{3}t+2\cos t\)\(0≤t≤2π.\) Kwa nyakati gani chembe hupumzika?
- Kidokezo
-
Tumia mfano uliopita kama mwongozo.
- Jibu
-
\(t=\dfrac{π}{3},\quad t=\dfrac{2π}{3}\)
Derivatives ya Kazi nyingine za Trigonomet
Kwa kuwa kazi nne zilizobaki za trigonometric zinaweza kuelezwa kama quotients zinazohusisha sine, cosine, au vyote viwili, tunaweza kutumia utawala wa quotient ili kupata fomu za derivatives zao.
Kupata derivative ya\(f(x)=\tan x.\)
Suluhisho
Anza kwa kuonyesha\(\tan x \) kama quotient ya\(\sin x\) na\(\cos x\):
\(f(x)=\tan x =\dfrac{\sin x}{\cos x}\).
Sasa tumia utawala wa quotient ili kupata
\(f′(x)=\dfrac{\cos x\cos x−(−\sin x)\sin x}{(\cos x)^2}\).
Kurahisisha, sisi kupata
\[f′(x)=\dfrac{\cos^2x+\sin^2 x}{\cos^2x}. \nonumber \]
Kutambua kwamba\(\cos^2x+\sin^2x=1,\) kwa theorem ya Pythagorean, sasa tuna
\[f′(x)=\dfrac{1}{\cos^2x} \nonumber \]
Hatimaye, kutumia utambulisho\(\sec x=\dfrac{1}{\cos x}\) kupata
\(f′(x)=\text{sec}^2 x\).
Kupata derivative ya\(f(x)=\cot x .\)
- Kidokezo
-
Andika upya\(\cot x \) kama\(\dfrac{\cos x}{\sin x}\) na utumie utawala wa quotient.
- Jibu
-
\(f′(x)=−\csc^2 x\)
Vipengee vya kazi zilizobaki za trigonometric zinaweza kupatikana kwa kutumia mbinu sawa. Tunatoa kanuni hizi katika theorem ifuatayo.
Vipengee vya kazi zilizobaki za trigonometric ni kama ifuatavyo:
\ [kuanza {align}\ dfrac {d} {dx} (\ tan x) &=\ sec ^ 2x\\ [4pt]
\ dfrac {d} {d} {dx} (\ cot x) &=\\ csc^2x\\ [4pt]
\ dfrac {d} {dx} (\ sec x) &=\ sec x\\ tan x\\ [4pt]
\ dfrac {d} {dx} (\ csc x) &=\ csc x\ cot x.\ mwisho {align}\ nonumber\]
Kupata equation ya tangent line kwa grafu ya\(f(x)=\cot x \) saa\(x=\frac{π}{4}\).
Suluhisho
Ili kupata equation ya mstari wa tangent, tunahitaji uhakika na mteremko wakati huo. Ili kupata uhakika, compute
\(f\left(\frac{π}{4}\right)=\cot\frac{π}{4}=1\).
Hivyo mstari wa tangent hupita kupitia hatua\(\left(\frac{π}{4},1\right)\). Kisha, tafuta mteremko kwa kutafuta derivative ya\(f(x)=\cot x \) na kutathmini kwa\(\frac{π}{4}\):
\(f′(x)=−\csc^2 x\)na\(f′\left(\frac{π}{4}\right)=−\csc^2\left(\frac{π}{4}\right)=−2\).
Kutumia equation ya mteremko wa mstari, tunapata
\(y−1=−2\left(x−\frac{π}{4}\right)\)
au sawasawa,
\(y=−2x+1+\frac{π}{2}\).
Kupata derivative ya\(f(x)=\csc x+x\tan x .\)
Suluhisho
Ili kupata derivative hii, tunapaswa kutumia utawala wa jumla na utawala wa bidhaa. Kutumia utawala wa jumla, tunapata
\(f′(x)=\dfrac{d}{dx}(\csc x)+\dfrac{d}{dx}(x\tan x )\).
Katika kipindi cha kwanza,\(\dfrac{d}{dx}(\csc x)=−\csc x\cot x ,\) na kwa kutumia utawala wa bidhaa kwa muda wa pili tunapata
\(\dfrac{d}{dx}(x\tan x )=(1)(\tan x )+(\sec^2 x)(x)\).
Kwa hiyo, tuna
\(f′(x)=−\csc x\cot x +\tan x +x\sec^2 x\).
Kupata derivative ya\(f(x)=2\tan x −3\cot x .\)
- Kidokezo
-
Tumia utawala wa kutofautisha mara nyingi mara kwa mara na utawala wa kutofautisha tofauti ya kazi mbili.
- Jibu
-
\(f′(x)=2\sec^2 x+3\csc^2 x\)
Pata mteremko wa mstari wa tangent kwenye grafu ya\(f(x)=\tan x \) saa\(x=\dfrac{π}{6}\).
- Kidokezo
-
Tathmini derivative katika\(x=\dfrac{π}{6}\).
- Jibu
-
\(\dfrac{4}{3}\)
Derivatives ya juu
derivatives ya juu-ili ya\(\sin x\) na\(\cos x\) kufuata mfano kurudia. Kwa kufuata mfano, tunaweza kupata yoyote derivative juu-ili ya\(\sin x\) na\(\cos x.\)
Kupata kwanza derivatives nne ya\(y=\sin x.\)
Suluhisho
Kila hatua katika mlolongo ni moja kwa moja:
\ [kuanza {align*} y&=\ dhambi x\\ [4pt]
\ dfrac {dy} {dx} &=\ cos x\\ [4pt]
\ dfrac {d ^ 2y} {dx^2} &=\\ dhambi x\\ [4pt]
\ dfrac {d ^ 3y} {d^3} &=\\ cos x\\ [4pt]\ [4 pt]
\ dfrac {d ^ 4y} {dx^4} &=\ dhambi x\ mwisho {align*}\]
Uchambuzi
Mara tu tunatambua muundo wa derivatives, tunaweza kupata derivative yoyote ya juu-ili kwa kuamua hatua katika muundo ambayo inafanana. Kwa mfano, kila derivative nne ya\(\sin x\) sawa\(\sin x\), hivyo
\[\dfrac{d^4}{dx^4}(\sin x)=\dfrac{d^8}{dx^8}(\sin x)=\dfrac{d^{12}}{dx^{12}}(\sin x)=…=\dfrac{d^{4n}}{dx^{4n}}(\sin x)=\sin x \nonumber \]
\[\dfrac{d^5}{dx^5}(\sin x)=\dfrac{d^9}{dx^9}(\sin x)=\dfrac{d^{13}}{dx^{13}}(\sin x)=…=\dfrac{d^{4n+1}}{dx^{4n+1}}(\sin x)=\cos x. \nonumber \]
Kwa\(y=\cos x\), kupata\(\dfrac{d^4y}{dx^4}\).
- Kidokezo
-
Angalia mfano uliopita.
- Jibu
-
\(\cos x\)
Kupata\(\dfrac{d^{74}}{dx^{74}}(\sin x)\).
Suluhisho
Tunaweza kuona mara moja kwamba kwa derivative 74 ya\(\sin x\)\(74=4(18)+2\), hivyo
\[\dfrac{d^{74}}{dx^{74}}(\sin x)=\dfrac{d^{72+2}}{dx^{72+2}}(\sin x)=\dfrac{d^2}{dx^2}(\sin x)=−\sin x. \nonumber \]
Kwa\(y=\sin x\), kupata\(\dfrac{d^{59}}{dx^{59}}(\sin x).\)
- Kidokezo
-
\(\dfrac{d^{59}}{dx^{59}}(\sin x)=\dfrac{d^{4⋅14+3}}{dx^{4⋅14+3}}(\sin x)\)
- Jibu
-
\(−\cos x\)
Chembe inakwenda kando ya mhimili wa kuratibu kwa namna ambayo msimamo wake wakati\(t\) unapewa na\(s(t)=2−\sin t\). Kupata\(v(π/4)\) na\(a(π/4)\). Linganisha maadili haya na uamua kama chembe inaharakisha au kupunguza kasi.
Suluhisho
Pata kwanza\(v(t)=s′(t)\)
\[v(t)=s′(t)=−\cos t . \nonumber \]
Hivyo,
\(v\left(\frac{π}{4}\right)=−\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}\).
Kisha, tafuta\(a(t)=v′(t)\). Hivyo,\(a(t)=v′(t)=\sin t\) na tuna
\(a\left(\frac{π}{4}\right)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\).
Tangu\(v\left(\frac{π}{4}\right)=−\dfrac{\sqrt{2}}{2}<0\) na\(a\left(\frac{π}{4}\right)=\dfrac{\sqrt{2}}{2}>0\), tunaona kwamba kasi na kuongeza kasi hufanya kwa njia tofauti; yaani, kitu kinaharakishwa katika mwelekeo kinyume na mwelekeo ambao unasafiri. Kwa hiyo, chembe inapunguza kasi.
Kizuizi kilichounganishwa na chemchemi kinasonga kwa wima. Msimamo wake wakati ni kutolewa na\(s(t)=2\sin t\). Kupata\(v\left(\frac{5π}{6}\right)\) na\(a\left(\frac{5π}{6}\right)\). Linganisha maadili haya na uamua kama block inaharakisha au kupunguza kasi.
- Kidokezo
-
Tumia Mfano\(\PageIndex{9}\) kama mwongozo.
- Jibu
-
\(v\left(\frac{5π}{6}\right)=−\sqrt{3}<0\)na\(a\left(\frac{5π}{6}\right)=−1<0\). Kizuizi kinaharakisha.
Dhana muhimu
- Tunaweza kupata derivatives ya\(\sin x\) na\(\cos x\) kwa kutumia ufafanuzi wa derivative na kikomo formula kupatikana mapema. Matokeo ni
\(\dfrac{d}{dx}\big(\sin x\big)=\cos x\quad\text{and}\quad\dfrac{d}{dx}\big(\cos x\big)=−\sin x\).
- Kwa kanuni hizi mbili, tunaweza kuamua derivatives ya kazi zote sita za msingi za trigonometric.
Mlinganyo muhimu
- Derivative ya kazi sine
\(\dfrac{d}{dx}(\sin x)=\cos x\)
- Derivative ya kazi ya cosine
\(\dfrac{d}{dx}(\cos x)=−\sin x\)
- Derivative ya kazi tangent
\(\dfrac{d}{dx}(\tan x )=\sec^2x\)
- Derivative ya kazi ya cotangent
\(\dfrac{d}{dx}(\cot x )=−\csc^2x\)
- Derivative ya kazi ya secant
\(\dfrac{d}{dx}(\sec x)=\sec x\tan x \)
- Derivative ya kazi ya cosecant
\(\dfrac{d}{dx}(\csc x)=−\csc x\cot x \)


