3.3: Kanuni za kutofautisha
- Page ID
- 178914
- Hali ya mara kwa mara, mara kwa mara nyingi, na sheria za nguvu.
- Tumia sheria za jumla na tofauti ili kuchanganya derivatives.
- Tumia utawala wa bidhaa kwa kutafuta derivative ya bidhaa ya kazi.
- Tumia utawala wa quotient kwa kutafuta derivative ya quotient ya kazi.
- Kupanua utawala wa nguvu kwa kazi na vielelezo hasi.
- Kuchanganya sheria za kutofautisha ili kupata derivative ya kazi ya polynomial au ya busara.
Kupata derivatives ya kazi kwa kutumia ufafanuzi wa derivative inaweza kuwa ndefu na, kwa kazi fulani, mchakato badala ya changamoto. Kwa mfano, hapo awali tuligundua kuwa
\[\dfrac{d}{dx}\left(\sqrt{x}\right)=\dfrac{1}{2\sqrt{x}} \nonumber \]
kwa kutumia mchakato ambao ulihusisha kuzidisha kujieleza kwa conjugate kabla ya kutathmini kikomo.
Mchakato ambao tunaweza kutumia kutathmini\(\dfrac{d}{dx}\left(\sqrt[3]{x}\right)\) kutumia ufafanuzi, wakati huo huo, ni ngumu zaidi.
Katika sehemu hii, tunaendeleza sheria za kutafuta derivatives ambazo zinatuwezesha kupitisha mchakato huu. Tunaanza na misingi.
Kanuni za Msingi
Kazi\(f(x)=c\) na\(g(x)=x^n\) wapi\(n\) integer chanya ni vitalu vya ujenzi ambavyo polynomials zote na kazi za busara zinajengwa. Ili kupata derivatives ya polynomials na kazi za busara kwa ufanisi bila kutumia ufafanuzi wa kikomo wa derivative, lazima kwanza tuendelee kuunda fomu za kutofautisha kazi hizi za msingi.
Utawala wa Mara kwa mara
Tunatumia kwanza ufafanuzi wa kikomo wa derivative ili kupata derivative ya kazi ya mara kwa mara,\(f(x)=c\). Kwa kazi hii, wote\(f(x)=c\) na\(f(x+h)=c\), hivyo sisi kupata matokeo yafuatayo:
\[\begin{align*} f′(x) &=\lim_{h→0} \dfrac{f(x+h)−f(x)}{h} \\[4pt] &=\lim_{h→0}\dfrac{c−c}{h} \\[4pt] &=\lim_{h→0}\dfrac{0}{h} \\[4pt] &=\lim_{h→0}0=0. \end{align*}\]
Utawala wa kutofautisha kazi za mara kwa mara huitwa utawala wa mara kwa mara. Inasema kuwa derivative ya kazi ya mara kwa mara ni sifuri; yaani, tangu kazi ya mara kwa mara ni mstari wa usawa, mteremko, au kiwango cha mabadiliko, ya kazi ya mara kwa mara ni\(0\). Tunarudia tena sheria hii katika theorem ifuatayo.
Hebu\(c\) kuwa mara kwa mara. Ikiwa\(f(x)=c\), basi\(f′(x)=0.\)
Vinginevyo, tunaweza kueleza sheria hii kama
\[\dfrac{d}{dx}(c)=0. \nonumber \]
Kupata derivative ya\(f(x)=8.\)
Suluhisho
Hii ni matumizi ya hatua moja tu ya utawala:\(f′(8)=0.\)
Kupata derivative ya\(g(x)=−3\).
- Kidokezo
-
Tumia mfano uliotangulia kama mwongozo
- Jibu
-
0
Utawala wa Nguvu
Tumeonyesha kwamba
\[\dfrac{d}{dx}\left(x^2\right)=2x\quad\text{ and }\quad\dfrac{d}{dx}\left(x^{1/2}\right)=\dfrac{1}{2}x^{−1/2}. \nonumber \]
Kwa hatua hii, unaweza kuona mfano unaoanza kuendeleza kwa derivatives ya fomu\(\dfrac{d}{dx}\left(x^n\right)\). Tunaendelea uchunguzi wetu wa formula za derivative kwa kutofautisha kazi za nguvu za fomu\(f(x)=x^n\) ambapo\(n\) ni integer nzuri. Sisi kuendeleza formula kwa derivatives ya aina hii ya kazi katika hatua, kuanzia na nguvu chanya integer. Kabla ya kusema na kuthibitisha utawala wa jumla wa derivatives ya kazi za fomu hii, tunaangalia kesi maalum,\(\dfrac{d}{dx}(x^3)\). Tunapopitia njia hii, kulipa kipaumbele maalum kwa sehemu ya kujieleza kwa ujasiri, kama mbinu inayotumiwa katika kesi hii ni sawa na mbinu inayotumiwa kuthibitisha kesi ya jumla.
Kupata\(\dfrac{d}{dx}\left(x^3\right)\).
Suluhisho:
| \(\displaystyle \dfrac{d}{dx}\left(x^3\right)=\lim_{h→0}\dfrac{(x+h)^3−x^3}{h}\) | |
| \(\displaystyle =\lim_{h→0}\dfrac{x^3+3x^2h+3xh^2+h^3−x^3}{h}\) | Kumbuka kwamba muda wa kwanza katika upanuzi wa\((x+h)^3\) ni\(x^3\) na muda wa pili ni\(3x^2h\). Masharti mengine yote yana mamlaka ya\(h\) kuwa ni mbili au zaidi |
| \(\displaystyle =\lim_{h→0}\dfrac{3x^2h+3xh^2+h^3}{h}\) | Katika hatua hii\(x^3\) maneno yamefutwa, na kuacha masharti tu yaliyo na\(h\). |
| \(\displaystyle =\lim_{h→0}\dfrac{h(3x^2+3xh+h^2)}{h}\) | Factor nje sababu ya kawaida ya\(h\). |
| \(\displaystyle =\lim_{h→0}(3x^2+3xh+h^2)\) | Baada ya kufuta sababu ya kawaida ya\(h\), mrefu tu si zenye\(h\) ni\(3x^2\). |
| \(=3x^2\) | Hebu\(h\) kwenda\(0\). |
Kupata\(\dfrac{d}{dx}\left(x^4\right).\)
- Kidokezo
-
Tumia\((x+h)^4=x^4+4x^3h+6x^2h^2+4xh^3+h^4\) na ufuate utaratibu uliotajwa katika mfano uliotangulia.
- Jibu
-
\(\dfrac{d}{dx}\left(x^4\right) = 4x^3\)
Kama tutakavyoona, utaratibu wa kutafuta derivative ya fomu ya jumla\(f(x)=x^n\) ni sawa sana. Ingawa mara nyingi ni busara kutekeleza hitimisho la jumla kutoka kwa mifano maalum, tunaona kwamba wakati sisi kutofautisha\(f(x)=x^3\), nguvu\(x\) inakuwa mgawo wa\(x^2\) katika derivative na nguvu\(x\) katika derivative hupungua kwa 1. Theorem zifuatazo inasema kwamba utawala nguvu ana kwa nguvu zote chanya integer ya\(x\). Sisi hatimaye kupanua matokeo haya kwa nguvu hasi integer. Baadaye, tutaona kwamba sheria hii pia inaweza kupanuliwa kwanza kwa mamlaka ya busara ya\(x\) na kisha kwa mamlaka holela ya\(x\). Jihadharini, hata hivyo, kwamba sheria hii haitumiki kwa kazi ambazo mara kwa mara hufufuliwa kwa nguvu ya kutofautiana, kama vile\(f(x)=3^x\).
Hebu\(n\) kuwa integer chanya. Ikiwa\(f(x)=x^n\), basi
\[f′(x)=nx^{n−1}. \nonumber \]
Vinginevyo, tunaweza kueleza sheria hii kama
\[\dfrac{d}{dx}\left(x^n\right)=nx^{n−1.} \nonumber \]
Kwa\(f(x)=x^n\)\(n\) wapi integer chanya, tuna
\[f′(x)=\lim_{h→0}\dfrac{(x+h)^n−x^n}{h}. \nonumber \]
Tangu
\((x+h)^n=x^n+nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n,\)
tunaona kwamba
\((x+h)^n−x^n=nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n.\)
Kisha, ugawanye pande zote mbili kwa h:
\(\dfrac{(x+h)^n−x^n}{h}=\dfrac{nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n}{h}.\)
Hivyo,
\(\dfrac{(x+h)^n−x^n}{h}=nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n−1}.\)
Hatimaye,
\[f′(x)=\lim_{h→0}(nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n-1}) \nonumber \]
\(=nx^{n−1}.\)
□
Pata derivative ya kazi\(f(x)=x^{10}\) kwa kutumia utawala wa nguvu.
Suluhisho
Kutumia utawala wa nguvu na\(n=10\), tunapata
\[f'(x)=10x^{10−1}=10x^9. \nonumber \]
Kupata derivative ya\(f(x)=x^7\).
- Kidokezo
-
Tumia utawala wa nguvu na\(n=7.\)
- Jibu
-
\(f′(x)=7x^6\)
Jumla, Tofauti, na Kanuni nyingi za Mara kwa mara
Tunapata sheria zetu za kutofautisha zifuatazo kwa kuangalia derivatives ya kiasi, tofauti, na wingi wa kazi mara kwa mara. Kama vile tunapofanya kazi na kazi, kuna sheria ambazo zinawezesha kupata derivatives ya kazi tunayoongeza, kuondoa, au kuzidisha kwa mara kwa mara. Sheria hizi zimefupishwa katika theorem ifuatayo.
Hebu\(f(x)\) na\(g(x)\) uwe na kazi tofauti na\(k\) uwe mara kwa mara. Kisha kila moja ya milinganyo yafuatayo inashikilia.
Jumla Utawala. derivative ya jumla ya kazi\(f\) na kazi\(g\) ni sawa na jumla ya derivative ya\(f\) na derivative ya\(g\).
\[\dfrac{d}{dx}\big(f(x)+g(x)\big)=\dfrac{d}{dx}\big(f(x)\big)+\dfrac{d}{dx}\big(g(x)\big); \nonumber \]
yaani,
\[\text{for }s(x)=f(x)+g(x),\quad s′(x)=f′(x)+g′(x). \nonumber \]
Tofauti Utawala. Derivative ya tofauti ya kazi\(f\) na kazi\(g\) ni sawa na tofauti ya derivative ya\(f\) na derivative ya\(g\):
\[\dfrac{d}{dx}(f(x)−g(x))=\dfrac{d}{dx}(f(x))−\dfrac{d}{dx}(g(x)); \nonumber \]
yaani,
\[\text{for }d(x)=f(x)−g(x),\quad d′(x)=f′(x)−g′(x). \nonumber \]
Mara kwa mara nyingi Utawala. Derivative ya mara kwa mara\(k\) kuongezeka kwa kazi\(f\) ni sawa na mara kwa mara kuongezeka kwa derivative:
\[\dfrac{d}{dx}\big(kf(x)\big)=k\dfrac{d}{dx}\big(f(x)\big); \nonumber \]
yaani,
\[\text{for }m(x)=kf(x),\quad m′(x)=kf′(x). \nonumber \]
Tunatoa tu ushahidi wa utawala wa jumla hapa. Wengine wanafuata kwa namna hiyo.
Kwa kazi tofauti\(f(x)\) na\(g(x)\), sisi kuweka\(s(x)=f(x)+g(x)\). Kutumia ufafanuzi wa kikomo wa derivative tuna
\[s′(x)=\lim_{h→0}\dfrac{s(x+h)−s(x)}{h}.\nonumber \]
Kwa kubadilisha\(s(x+h)=f(x+h)+g(x+h)\) na\(s(x)=f(x)+g(x),\) sisi kupata
\[s′(x)=\lim_{h→0}\dfrac{\big(f(x+h)+g(x+h)\big)−\big(f(x)+g(x)\big)}{h}.\nonumber \]
Rearranging na regrouping masharti, tuna
\[s′(x)=\lim_{h→0}\left(\dfrac{f(x+h)−f(x)}{h}+\dfrac{g(x+h)−g(x)}{h}\right).\nonumber \]
Sisi sasa kutumia sheria jumla kwa ajili ya mipaka na ufafanuzi wa derivative kupata
\[s′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}+\lim_{h→0}\dfrac{g(x+h)−g(x)}{h}=f′(x)+g′(x).\nonumber \]
□
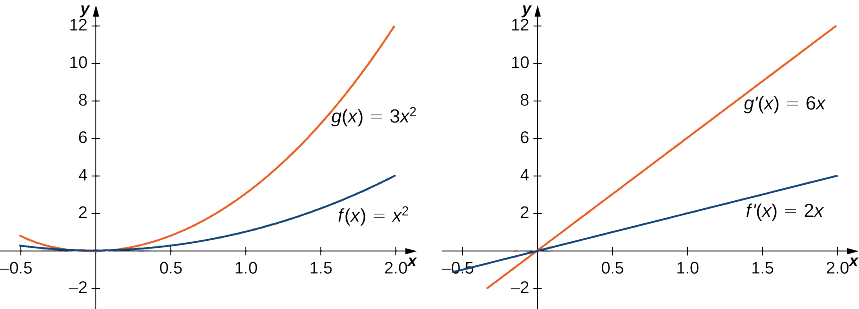
Find derivative ya\(g(x)=3x^2\) na kulinganisha na derivative ya\(f(x)=x^2.\)
Suluhisho
Tunatumia utawala wa nguvu moja kwa moja:
\[g′(x)=\dfrac{d}{dx}(3x^2)=3\dfrac{d}{dx}(x^2)=3(2x)=6x.\nonumber \]
Kwa kuwa\(f(x)=x^2\) ina derivative\(f′(x)=2x\), tunaona kwamba derivative ya\(g(x)\) ni 3 mara derivative ya\(f(x)\). Uhusiano huu ni mfano katika Kielelezo\(\PageIndex{1}\).
Kupata derivative ya\(f(x)=2x^5+7\).
Suluhisho
Tunaanza kwa kutumia utawala wa kutofautisha jumla ya kazi mbili, ikifuatiwa na sheria za kutofautisha kazi nyingi za mara kwa mara na utawala wa kutofautisha nguvu. Ili kuelewa vizuri mlolongo ambao sheria za kutofautisha zinatumika, tunatumia maelezo ya Leibniz katika suluhisho:
\ (\ kuanza {align*} f′ (x) &=\ dfrac {d} {dx}\ kushoto (2x ^ 5+7\ haki)\\ [4pt]
&=\ dfrac {d} {dx} {dx} (2x^5) +\ dfrac {d} {dx} (7) &\ maandishi {Tumia utawala wa jumla.}\\ [4pt]
&=2\ dfrac {d} {dx} (x ^ 5) +\ dfrac {d} {dx} (7) & &\ maandishi {Weka utawala mara kwa mara nyingi.}\\ [4pt]
&=2 (5 x ^ 4) +0 & &\ maandishi {Tumia utawala wa nguvu na utawala wa mara kwa mara.}\\ [4pt]
&=10x ^ 4 & &\ maandishi {Kurahisisha.} \ mwisho {align*}\)
Kupata derivative ya\(f(x)=2x^3−6x^2+3.\)
- Kidokezo
-
Tumia mfano uliotangulia kama mwongozo.
- Jibu
-
\(f′(x)=6x^2−12x.\)
Kupata equation ya tangent line kwa grafu ya\(f(x)=x^2−4x+6\) saa\(x=1\)
Suluhisho
Ili kupata equation ya mstari wa tangent, tunahitaji uhakika na mteremko. Ili kupata uhakika, compute
\[f(1)=1^2−4(1)+6=3. \nonumber \]
Hii inatupa uhakika\((1,3)\). Tangu mteremko wa mstari wa tangent saa 1 ni\(f′(1)\), lazima kwanza tupate\(f′(x)\). Kutumia ufafanuzi wa derivative, tuna
\[f′(x)=2x−4\nonumber \]
hivyo mteremko wa mstari wa tangent ni\(f′(1)=−2\). Kutumia formula ya mteremko wa uhakika, tunaona kwamba equation ya mstari wa tangent ni
\[y−3=−2(x−1).\nonumber \]
Kuweka equation ya mstari katika fomu ya mteremko, tunapata
\[y=−2x+5.\nonumber \]
Kupata equation ya tangent line kwa grafu ya\(f(x)=3x^2−11\) saa\(x=2\). Tumia fomu ya mteremko wa uhakika.
- Kidokezo
-
Tumia mfano uliotangulia kama mwongozo.
- Jibu
-
\(y=12x−23\)
Utawala wa Bidhaa
Sasa kwa kuwa tumechunguza sheria za msingi, tunaweza kuanza kuangalia baadhi ya sheria za juu zaidi. Ya kwanza inachunguza derivative ya bidhaa ya kazi mbili. Ingawa huenda ikajaribu kudhani kuwa derivative ya bidhaa ni bidhaa ya derivatives, sawa na sheria za jumla na tofauti, utawala wa bidhaa haufuati mfano huu. Ili kuona kwa nini hatuwezi kutumia mfano huu, fikiria kazi\(f(x)=x^2\), ambaye derivative ni\(f′(x)=2x\) na si\(\dfrac{d}{dx}(x)⋅\dfrac{d}{dx}(x)=1⋅1=1.\)
Hebu\(f(x)\) na\(g(x)\) uwe na kazi tofauti. Kisha
\[\dfrac{d}{dx}(f(x)g(x))=\dfrac{d}{dx}(f(x))⋅g(x)+\dfrac{d}{dx}(g(x))⋅f(x). \nonumber \]
Hiyo ni,
\[\text{if }p(x)=f(x)g(x),\quad \text{then }p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
Hii ina maana kwamba derivative ya bidhaa ya kazi mbili ni derivative ya mara ya kwanza kazi ya pili, pamoja na derivative ya kazi ya pili mara kazi ya kwanza.
Tunaanza kwa\(f(x)\) kudhani kwamba na\(g(x)\) ni kazi tofauti. Katika hatua muhimu katika ushahidi huu tunahitaji kutumia ukweli kwamba,\(g(x)\) kwa kuwa ni tofauti, pia ni kuendelea. Hasa, sisi kutumia ukweli kwamba tangu\(g(x)\) ni kuendelea,\(\displaystyle \lim_{h→0}g(x+h)=g(x).\)
Kwa kutumia ufafanuzi kikomo ya derivative kwa\(p(x)=f(x)g(x),\) sisi kupata
\[ p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Kwa kuongeza na kuondoa\(f(x)g(x+h)\) katika nambari, tuna
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Baada ya kuvunja quotient hii na kutumia sheria ya jumla kwa mipaka, derivative inakuwa
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)}{h}+\lim_{h→0}\dfrac{f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Kupanga upya, tunapata
\ [kuanza {align*} p( x) &=\ lim_ {h→ 0}\ kushoto (\ dfrac {f (x+h) -f (x)} {h} g (x+h)\ kulia) +\ lim_ {h → 0}\ kushoto (\ dfrac {g (x+h) -g (x)} {h} f (x)\ haki)\\ [4pt]
&=\ kushoto (\ lim_ {h → 0}\ dfrac {f (x+h) -f (x)} {h}\ haki) 合\ kushoto (\ lim_ {h → 0}\ g (x+h)\ haki) +\ kushoto (\ lim_ {h → 0}\ dfrac {g (x+h) -g (x)} {h}\ haki) f (x)\ mwisho {align*}\]
Kwa kutumia mwendelezo wa\(g(x)\), ufafanuzi wa derivatives ya\(f(x)\) na\(g(x)\), na kutumia sheria kikomo, sisi kufika katika utawala wa bidhaa,
\[p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
□
Kwa\(p(x)=f(x)g(x)\), kutumia utawala wa bidhaa ili kujua\(p′(2)\) kama\(f(2)=3,\; f′(2)=−4,\; g(2)=1\), na\(g′(2)=6\).
Suluhisho
Tangu\(p(x)=f(x)g(x)\),\(p′(x)=f′(x)g(x)+g′(x)f(x),\) na hivyo
\(p′(2)=f′(2)g(2)+g′(2)f(2)=(−4)(1)+(6)(3)=14.\)
Kwa\(p(x)=(x^2+2)(3x^3−5x),\) kupata\(p′(x)\) kwa kutumia utawala wa bidhaa. Angalia matokeo kwa kutafuta kwanza bidhaa na kisha kutofautisha.
Suluhisho
Ikiwa tunaweka\(f(x)=x^2+2\) na\(g(x)=3x^3−5x\), basi\(f′(x)=2x\) na\(g′(x)=9x^2−5\). Hivyo,
\(p′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3x^3−5x)+(9x^2−5)(x^2+2).\)
Kurahisisha, tuna
\[p′(x)=15x^4+3x^2−10. \nonumber \]
Kuangalia, tunaona kwamba,\(p(x)=3x^5+x^3−10x\) na hivyo,\(p′(x)=15x^4+3x^2−10.\)
Matumizi ya utawala wa bidhaa ili kupata derivative ya\(p(x)=2x^5(4x^2+x).\)
- Kidokezo
-
Weka\(f(x)=2x^5\)\(g(x)=4x^2+x\) na utumie mfano uliotangulia kama mwongozo.
- Jibu
-
\(p′(x)=10x^4(4x^2+x)+(8x+1)(2x^5)=56x^6+12x^5.\)
Utawala wa Quotient
Baada ya kuendeleza na kutekeleza utawala wa bidhaa, sasa tunazingatia kutofautisha quotients ya kazi. Kama tunavyoona katika theorem ifuatayo, derivative ya quotient sio quotient ya derivatives; badala yake, ni derivative ya kazi katika nyakati za nambari kazi katika denominator bala derivative ya kazi katika nyakati za denominator kazi katika nambari, yote imegawanywa na mraba wa kazi katika denominator. Ili kuelewa vizuri kwa nini hatuwezi tu kuchukua quotient ya derivatives, kukumbuka kwamba
\[\dfrac{d}{dx}(x^2)=2x,\text{ not }\dfrac{\dfrac{d}{dx}(x^3)}{\dfrac{d}{dx}(x)}=\dfrac{3x^2}{1}=3x^2.\nonumber \]
Hebu\(f(x)\) na\(g(x)\) uwe na kazi tofauti. Kisha
\[\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{\dfrac{d}{dx}(f(x))⋅g(x)−\dfrac{d}{dx}(g(x))⋅f(x)}{\big(g(x)\big)^2}. \nonumber \]
Hiyo ni, kama
\[q(x)=\dfrac{f(x)}{g(x)}\nonumber \]
basi
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}.\nonumber \]
Ushahidi wa utawala wa quotient ni sawa na ushahidi wa utawala wa bidhaa, kwa hiyo umeondolewa hapa. Badala yake, tunatumia sheria hii mpya ya kutafuta derivatives katika mfano unaofuata.
Kutumia utawala quotient kupata derivative ya\(q(x)=\dfrac{5x^2}{4x+3}.\)
Suluhisho
Hebu\(f(x)=5x^2\) na\(g(x)=4x+3\). Hivyo,\(f′(x)=10x\) na\(g′(x)=4\).
Kubadilisha katika utawala wa quotient, tuna
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{(g(x))^2}=\dfrac{10x(4x+3)−4(5x^2)}{(4x+3)^2}.\nonumber \]
Kurahisisha, tunapata
\[q′(x)=\dfrac{20x^2+30x}{(4x+3)^2}\nonumber \]
Kupata derivative ya\(h(x)=\dfrac{3x+1}{4x−3}\).
- Kidokezo
-
Tumia utawala wa quotient\(f(x)=3x+1\) na\(g(x)=4x−3\).
- Jibu
-
\(h′(x)=−\dfrac{13}{(4x−3)^2}.\)
Sasa inawezekana kutumia utawala wa quotient kupanua utawala wa nguvu ili kupata derivatives ya kazi za fomu\(x^k\) ambapo\(k\) ni integer hasi.
Ikiwa\(k\) ni integer hasi, basi
\[\dfrac{d}{dx}(x^k)=kx^{k−1}. \nonumber \]
Kama\(k\) ni integer hasi, tunaweza kuweka\(n=−k\), ili n ni integer chanya na\(k=−n\). Tangu kwa kila integer chanya\(n\)\(x^{−n}=\dfrac{1}{x^n}\),, tunaweza sasa kutumia utawala quotient kwa kuweka\(f(x)=1\) na\(g(x)=x^n\). Katika kesi hii,\(f′(x)=0\) na\(g′(x)=nx^{n−1}\). Hivyo,
\[\dfrac{d}{dx}(x^{−n})=\dfrac{0(x^n)−1(nx^{n−1})}{(x^n)^2}.\nonumber \]
Kurahisisha, tunaona kwamba
\[\begin{align*} \dfrac{d}{dx}(x^{−n}) &=\dfrac{−nx^{n−1}}{x^{2n}}\\[4pt]&=−nx^{(n−1)−2n}\\[4pt]&=−nx^{−n−1}.\end{align*}\]
Hatimaye, kuchunguza kwamba tangu\(k=−n\), kwa kubadilisha tuna
\[\dfrac{d}{dx}(x^k)=kx^{k−1}.\nonumber \]
□
Kupata\(\dfrac{d}{dx}(x^{−4})\).
Suluhisho
Kwa kutumia kupanuliwa nguvu utawala na\(k=−4\), sisi kupata
\[\dfrac{d}{dx}(x^{−4})=−4x^{−4−1}=−4x^{−5}.\nonumber \]
Tumia utawala wa nguvu uliopanuliwa na utawala wa mara kwa mara ili kupata\(f(x)=\dfrac{6}{x^2}\).
Suluhisho
Inaweza kuonekana kuwa inajaribu kutumia utawala wa quotient ili kupata derivative hii, na hakika haitakuwa sahihi kufanya hivyo. Hata hivyo, ni rahisi sana kutofautisha kazi hii kwa kuandika upya kwanza kama\(f(x)=6x^{−2}\).
\ (\ kuanza {align*} f′ (x) &=\ dfrac {d} {dx}\ kushoto (\ dfrac {6} {x ^ 2}\ haki) =\ dfrac {d} {dx}\ kushoto (6x^ {¯ 2}\ haki) & &\ maandishi {Andika upya}\ dfrac {6} {x ^ 2}\ maandishi kama {} 6x^ {¯ 2}.\\ [4pt]
&=6\ dfrac {d} {dx}\ kushoto (x^ {¯ 2}\ kulia) & &\ maandishi {Tumia utawala wa mara kwa mara nyingi.}\\ [4pt]
&=6 (-2x^ { -3}) & &\ maandishi {Tumia utawala wa nguvu kupanuliwa ili kutofautisha} x^ {¯ 2}.\\ [4pt]
&=-12x^ {˚ 3} &\ maandishi {kurahisisha.} \ mwisho {align*}\)
Pata derivative ya\(g(x)=\dfrac{1}{x^7}\) kutumia utawala wa nguvu uliopanuliwa.
- Kidokezo
-
Andika upya\(g(x)=\dfrac{1}{x^7}=x^{−7}\). Tumia utawala wa nguvu ulioongezwa na\(k=−7\).
- Jibu
-
\(g′(x)=−7x^{−8}\).
Kuchanganya Kanuni za Tofauti
Kama tulivyoona katika mifano katika sehemu hii, ni mara chache hutokea kwamba sisi ni wito juu ya kuomba moja tu upambanuzi utawala kupata derivative ya kazi fulani. Kwa hatua hii, kwa kuchanganya sheria za kutofautisha, tunaweza kupata derivatives ya kazi yoyote ya polynomial au ya busara. Baadaye tutakutana na mchanganyiko ngumu zaidi wa sheria za kutofautisha. Utawala mzuri wa kidole cha kutumia wakati wa kutumia sheria kadhaa ni kutumia sheria kinyume cha utaratibu ambao tutaweza kutathmini kazi.
Kwa\(k(x)=3h(x)+x^2g(x)\), kupata\(k′(x)\).
Suluhisho: Kupata derivative hii inahitaji utawala wa jumla, utawala wa mara kwa mara, na utawala wa bidhaa.
| \(k′(x)=\dfrac{d}{dx}\big(3h(x)+x^2g(x)\big)=\dfrac{d}{dx}\big(3h(x)\big)+\dfrac{d}{dx}\big(x^2g(x)\big)\) | Tumia utawala wa jumla. |
| \(=3\dfrac{d}{dx}\big(h(x)\big)+\left(\dfrac{d}{dx}(x^2)g(x)+\dfrac{d}{dx}(g(x))x^2\right)\) | Tumia utawala wa mara kwa mara ili kutofautisha\(3h(x)\) na utawala wa bidhaa ili kutofautisha\(x^2g(x)\). |
| \(=3h′(x)+2xg(x)+g′(x)x^2\) |
Kwa\(k(x)=f(x)g(x)h(x)\), kueleza\(k′(x)\) katika suala la\(f(x),g(x),h(x)\), na derivatives yao.
Suluhisho
Tunaweza kufikiria kazi\(k(x)\) kama bidhaa ya kazi\(f(x)g(x)\) na kazi\(h(x)\). Hiyo ni,\(k(x)=(f(x)g(x))⋅h(x)\). Hivyo,
\ (\ kuanza {align*} k( x) &=\ dfrac {d} {dx}\ kubwa (f (x) g (x)\ kubwa) h (x) +\ dfrac {d} {dx}\ kubwa (h (x)\ kubwa (f (x) g (x)\ kubwa). & &\ maandishi {Weka utawala wa bidhaa kwa bidhaa ya} f (x) g (x)\ maandishi {na} h (x).\\ [4pt]
&=\ kubwa (f) (x) g (x) +g (x) f (x) f (x)\ kubwa) h (x) +h (x) f (x) &\ maandishi {Tumia utawala wa bidhaa kwa} f (x) g (x)\\ [4pt]
&=f (x) g (x) h (x) +f (x) g (x) h (x) +f (x) g (x) h (x). & &\ maandishi {Kurahisisha.} \ mwisho {align*}\)
Kwa\(h(x)=\dfrac{2x^3k(x)}{3x+2}\), kupata\(h′(x)\).
Suluhisho
Utaratibu huu ni wa kawaida kwa kutafuta derivative ya kazi ya busara.
\ (\ kuanza {align*} h (x) &=\ dfrac {\ dfrac {d} {d} {dx} (2x^3k (x)) 合 (3x+2) -\ dfrac {d} {dx} (3x+2) {dx} (3x+2) {dfrac {d} (3x+2) {d} {dx} (3x+2) {dx} (3x+2) {d} {dx} (3x+2) {dx} (3x+2) {d} {dx} (3x+2) {d} utawala wa ent.}\\ [4pt]
&=\ dfrac {(6x ^ 2k (x) +k (x) 2x^3) (3x+2) -3 (2x^ 3k (x))} {(3x+2) ^2} & &\ maandishi {Tumia utawala wa bidhaa kupata}\ dfrac {d} {dx} (2x^3k (x)). \ maandishi {Matumizi}\ dfrac {d} {dx} (3x+2) =3.\\ [4pt]
&=\ dfrac {-6x^3k (x) +18x^3k (x) +12x^2k (x) +6x^4k (x) +4x^3k (x)} {(3x+2) ^2} &\ maandishi {Kurahisisha}\ mwisho {align*}\)
Kupata\(\dfrac{d}{dx}(3f(x)−2g(x)).\)
- Kidokezo
-
Tumia utawala tofauti na utawala wa mara kwa mara.
- Jibu
-
\(3f′(x)−2g′(x).\)
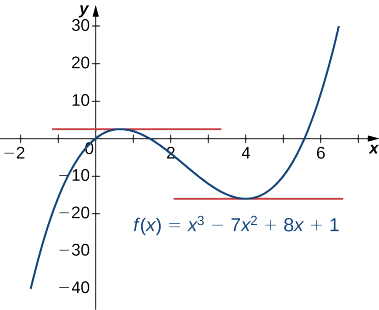
Tambua maadili ambayo\(f(x)=x^3−7x^2+8x+1\) ina mstari wa usawa wa tangent.\(x\)
Suluhisho
Ili kupata maadili ambayo\(f(x)\) ina mstari wa\(x\) usawa wa tangent, tunapaswa kutatua\(f′(x)=0\).
Tangu\(f′(x)=3x^2−14x+8=(3x−2)(x−4)\),
ni lazima kutatua\((3x−2)(x−4)=0\). Hivyo tunaona kwamba kazi ina usawa tangent mistari katika\(x=\dfrac{2}{3}\) na\(x=4\) kama inavyoonekana katika grafu zifuatazo.
Msimamo wa kitu kwenye mhimili wa kuratibu kwa wakati\(t\) hutolewa na kasi\(s(t)=\dfrac{t}{t^2+1}.\) gani ya awali ya kitu?
Suluhisho
Tangu kasi ya awali\(v(0)=s′(0),\) inaanza kwa kutafuta\(s′(t)\) kwa kutumia utawala wa quotient:
\(s′(t)=\dfrac{1(t^2+1)−2t(t)}{(t^2+1)^2}=\dfrac{1−t^2}{(t^2+1)^2}\).
Baada ya kutathmini, tunaona kwamba\(v(0)=1.\)
Pata maadili ambayo mstari wa\(x\) tangent kwenye grafu ya\(f(x)=4x^2−3x+2\) ina mstari wa tangent unaofanana na mstari\(y=2x+3.\)
- Kidokezo
-
Kutatua\(f′(x)=2\).
- Jibu
-
\(\dfrac{5}{8}\)
Mfumo One gari jamii inaweza kuwa ya kusisimua sana kuangalia na kuvutia watazamaji wengi. Mfumo One kufuatilia wabunifu na kuhakikisha kutosha grandstand nafasi inapatikana karibu kufuatilia kwa ajili ya malazi watazamaji hawa. Hata hivyo, racing ya gari inaweza kuwa hatari, na masuala ya usalama ni muhimu. Grandstands lazima kuwekwa ambapo watazamaji hawatakuwa katika hatari lazima dereva kupoteza udhibiti wa gari (Kielelezo\(\PageIndex{3}\)).

Usalama ni wasiwasi hasa juu ya zamu. Ikiwa dereva haipunguza kasi ya kutosha kabla ya kuingia upande, gari linaweza kuondokana na racetrack. Kwa kawaida, hii inasababisha tu kugeuka pana, ambayo hupunguza dereva chini. Lakini kama dereva kupoteza kudhibiti kabisa, gari inaweza kuruka mbali kufuatilia kabisa, juu ya njia tangent kwa Curve ya racetrack.
Tuseme wewe ni kubuni mpya Mfumo One kufuatilia. Sehemu moja ya wimbo inaweza kuonyeshwa na kazi\(f(x)=x^3+3x^2+x\) (Kielelezo\(\PageIndex{4}\)). Mpango wa sasa unatoa wito wa makuu kujengwa kando ya kwanza mara moja na karibu na sehemu ya pembe ya kwanza. Mipango wito kwa kona ya mbele ya grandstand kuwa iko katika hatua (\(−1.9,2.8\)). Tunataka kuamua kama eneo hili linaweka watazamaji katika hatari ikiwa dereva hupoteza udhibiti wa gari.
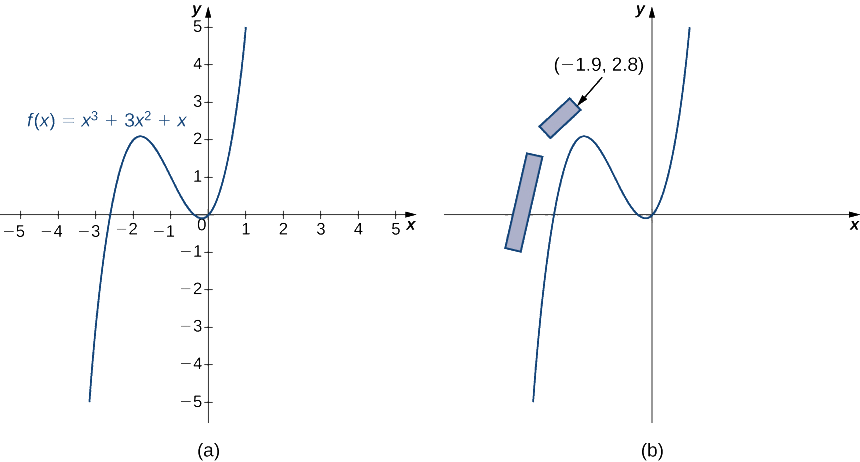
- Wataalamu wa Fizikia wameamua kuwa madereva wana uwezekano mkubwa wa kupoteza udhibiti wa magari yao kama wanakuja kugeuka, wakati ambapo mteremko wa mstari wa tangent ni 1. Pata\((x,y)\) kuratibu za hatua hii karibu na upande.
- Find equation ya mstari tangent kwa Curve katika hatua hii.
- Kuamua kama watazamaji wako katika hatari katika hali hii, tafuta\(x\) -kuratibu ya uhakika ambapo mstari wa tangent unavuka mstari\(y=2.8\). Je, hatua hii ni salama kwa haki ya grandstand? Au watazamaji katika hatari?
- Nini ikiwa dereva hupoteza udhibiti mapema kuliko mradi wa fizikia? Tuseme dereva hupoteza udhibiti katika hatua (\(−2.5,0.625\)). Je, ni mteremko wa mstari wa tangent wakati huu?
- Kama dereva kupoteza udhibiti kama ilivyoelezwa katika sehemu ya 4, watazamaji ni salama?
- Je, unapaswa kuendelea na kubuni ya sasa kwa ajili ya grandstand, au lazima grandstands kuhamishwa?
Dhana muhimu
- Derivative ya kazi ya mara kwa mara ni sifuri.
- Derivative ya kazi ya nguvu ni kazi ambayo nguvu\(x\) inakuwa mgawo wa muda na nguvu\(x\) katika derivative inapungua kwa 1.
- Derivative ya mara kwa mara\(c\) kuongezeka kwa kazi\(f\) ni sawa na mara kwa mara kuongezeka kwa derivative.
- derivative ya jumla ya kazi\(f\) na kazi\(g\) ni sawa na jumla ya derivative ya\(f\) na derivative ya\(g\).
- derivative ya tofauti ya kazi\(f\) na kazi\(g\) ni sawa na tofauti ya derivative ya\(f\) na derivative ya\(g\).
- Derivative ya bidhaa ya kazi mbili ni derivative ya mara ya kwanza kazi kazi ya pili pamoja na derivative ya kazi ya pili mara kazi ya kwanza.
- Derivative ya quotient ya kazi mbili ni derivative ya mara ya kwanza ya kazi, kazi ya pili bala derivative ya kazi ya pili mara kazi ya kwanza, yote imegawanywa na mraba wa kazi ya pili.
- Tulitumia ufafanuzi wa kikomo wa derivative kuendeleza formula ambazo zinatuwezesha kupata derivatives bila kutumia ufafanuzi wa derivative. Fomu hizi zinaweza kutumika peke yake au kwa pamoja.
faharasa
- utawala wa mara kwa mara
- derivative ya mara kwa mara\(c\) kuongezeka kwa kazi\(f\) ni sawa na mara kwa mara kuongezeka kwa derivative:\(\dfrac{d}{dx}\big(cf(x)\big)=cf′(x)\)
- utawala wa mara kwa mara
- derivative ya kazi ya mara kwa mara ni sifuri:\(\dfrac{d}{dx}(c)=0\), ambapo\(c\) ni mara kwa mara
- utawala tofauti
- derivative ya tofauti ya kazi\(f\) na kazi\(g\) ni sawa na tofauti ya derivative ya\(f\) na derivative ya\(g\):\(\dfrac{d}{dx}\big(f(x)−g(x)\big)=f′(x)−g′(x)\)
- utawala wa nguvu
- derivative ya kazi ya nguvu ni kazi ambayo nguvu\(x\) inakuwa mgawo wa muda na nguvu\(x\) katika derivative inapungua kwa 1: Kama\(n\) ni integer, basi\(\dfrac{d}{dx}\left(x^n\right)=nx^{n−1}\)
- utawala wa bidhaa
- derivative ya bidhaa ya kazi mbili ni derivative ya mara ya kwanza kazi kazi ya pili pamoja na derivative ya kazi ya pili mara kazi ya kwanza:\(\dfrac{d}{dx}\big(f(x)g(x)\big)=f′(x)g(x)+g′(x)f(x)\)
- utawala wa quotient
- derivative ya quotient ya kazi mbili ni derivative ya mara ya kwanza kazi kazi ya pili bala derivative ya kazi ya pili mara kazi ya kwanza, wote kugawanywa na mraba wa kazi ya pili:\(\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}\)
- jumla ya utawala
- derivative ya jumla ya kazi\(f\) na kazi\(g\) ni sawa na jumla ya derivative ya\(f\) na derivative ya\(g\):\(\dfrac{d}{dx}\big(f(x)+g(x)\big)=f′(x)+g′(x)\)


