2.5: Ufafanuzi sahihi wa Kikomo

Last updated
Save as PDF

Page ID: 178960

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Eleza ufafanuzi wa epsilon-delta wa kikomo.
Tumia ufafanuzi wa epsilon-delta ili kupata kikomo cha kazi.
Eleza ufafanuzi wa epsilon-delta wa mipaka ya upande mmoja na mipaka isiyo na mwisho.
Tumia ufafanuzi wa epsilon-delta ili kuthibitisha sheria za kikomo.

Kwa sasa una maendeleo kutoka ufafanuzi rasmi sana ya kikomo katika kuanzishwa kwa sura hii kwa uelewa angavu wa kikomo. Katika hatua hii, unapaswa kuwa na hisia kali sana ya Intuitive ya nini kikomo cha kazi ina maana na jinsi unaweza kupata hiyo. Katika sehemu hii, sisi kubadilisha wazo hili angavu ya kikomo katika ufafanuzi rasmi kwa kutumia lugha sahihi hisabati. Ufafanuzi rasmi wa kikomo ni uwezekano wa mojawapo ya ufafanuzi wenye changamoto zaidi utakutana mapema katika utafiti wako wa calculus; hata hivyo, ni pamoja na thamani ya jitihada yoyote unayoifanya ili kuipatanisha na wazo lako la kikomo. Kuelewa ufafanuzi huu ni ufunguo unaofungua mlango kwa ufahamu bora wa calculus.

Quantifying ukaribu

Kabla ya kusema ufafanuzi rasmi wa kikomo, ni lazima kuanzisha mawazo machache ya awali. Kumbuka kwamba umbali kati ya pointi mbili$a$ na$b$ kwenye mstari wa nambari hutolewa na |$a−b$ |.

taarifa |$f(x)−L |<ε$ inaweza kutafsiriwa kama: umbali kati$f(x)$ na$L$ ni chini ya$ε$.
Taarifa$0<|x−a|<δ$ inaweza kutafsiriwa kama:$x≠a$ na umbali kati$x$ na$a$ ni chini ya$δ$.

Pia ni muhimu kuangalia equivalences zifuatazo kwa thamani kamili:

Taarifa |$f(x)−L|<ε$ ni sawa na taarifa$L−ε<f(x)<L+ε$.
Taarifa$0<|x−a|<δ$ hiyo ni sawa na taarifa$a−δ<x<a+δ$ na$x≠a$.

Kwa ufafanuzi huu, tunaweza kusema ufafanuzi rasmi wa epsilon-delta wa kikomo.

Ufafanuzi: Mipaka ya mwisho (rasmi)

Hebu$f(x)$ kuelezwa kwa$x≠a$ muda wote wa wazi ulio na$a$. Hebu$L$ kuwa idadi halisi. Kisha

\[\lim_{x→a}f(x)=L \nonumber \]

kama, kwa kila$ε>0$, kuna$δ>0$, kama kwamba kama$0<|x−a|<δ$, basi$|f(x)−L|<ε$.

Ufafanuzi huu unaweza kuonekana kuwa ngumu kutoka kwa mtazamo wa hisabati, lakini inakuwa rahisi kuelewa ikiwa tunaivunja maneno kwa maneno. Taarifa yenyewe inahusisha kitu kinachoitwa quantifier zima (kwa kila$ε>0$), quantifier iliyopo (kuna$δ>0$), na, mwisho, taarifa ya masharti (ikiwa$0<|x−a|<δ$, basi$|f(x)−L|<ε)$. Hebu tuangalie Jedwali$\PageIndex{1}$, ambalo linavunja ufafanuzi na hutafsiri kila sehemu.

Jedwali$\PageIndex{1}$
Ufafanuzi	Tafsiri
1. Kwa kila$ε>0$,	1. Kwa kila umbali chanya$ε$ kutoka$L$,
2. kuna$δ>0$,	2. Kuna umbali chanya$δ$ kutoka$a$,
3. vile	3. vile
4. ikiwa$0<\|x−a\|<δ$, basi$\|f(x)−L\|<ε$.	4. ikiwa$x$ ni$δ$ karibu kuliko$a$ na$x≠a$, basi$f(x)$ ni$ε$ karibu kuliko$L$.

Tunaweza kupata kushughulikia bora juu ya ufafanuzi huu kwa kuangalia ufafanuzi kijiometri. Kielelezo$\PageIndex{1}$ inaonyesha maadili ya uwezekano wa$δ$ kwa$ε>0$ ajili ya uchaguzi mbalimbali ya kwa ajili ya kazi$f(x)$ fulani$a$, idadi, na kikomo$L$ katika$a$. Kumbuka kwamba kama sisi kuchagua maadili ndogo ya$ε$ (umbali kati ya kazi na kikomo), tunaweza daima kupata$δ$ ndogo ya kutosha ili kama tumechagua$x$ thamani ndani$δ$ ya$a$, basi thamani ya$f(x)$ ni ndani$ε$ ya kikomo $L$.

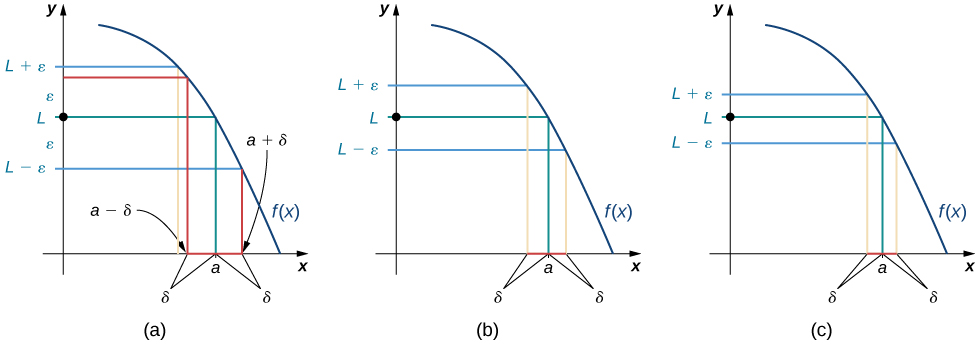
Kuna grafu tatu upande kwa upande kuonyesha maadili iwezekanavyo ya delta, kutokana na uchaguzi mfululizo ndogo ya epsilon. Kila grafu ina kupungua, concave chini Curve katika roboduara moja. Kila grafu ina uhakika (a, L) alama juu ya Curve, ambapo L ni kikomo cha kazi katika hatua ambapo x = a. upande wowote wa L kwenye y mhimili, umbali epsilon ni alama mbali - yaani, line ni inayotolewa kwa njia ya kazi katika y = L + epsilon na L — epsilon. Kama maadili madogo ya epsilon huchaguliwa kutoka kwenye grafu moja hadi grafu tatu, maadili madogo ya delta upande wa kushoto na kulia wa kumweka a yanaweza kupatikana ili ikiwa tumechagua thamani x ndani ya delta ya, basi thamani ya f (x) iko ndani ya epsilon ya kikomo L. — Kielelezo$\PageIndex{1}$: Grafu hizi zinaonyesha maadili iwezekanavyo ya$δ$, kutokana uchaguzi mfululizo ndogo ya$ε$.

Kumbuka

Ziara applet zifuatazo kwa majaribio na kutafuta maadili ya$δ$ kwa ajili ya maadili ya kuchaguliwa ya$ε$:

Ufafanuzi wa epsilon-delta wa kikomo

Mfano$\PageIndex{1}$ unaonyesha jinsi unavyoweza kutumia ufafanuzi huu kuthibitisha taarifa kuhusu kikomo cha kazi maalum kwa thamani maalum.

Mfano$\PageIndex{1}$: Proving a Statement about the Limit of a Specific Function

Thibitisha kwamba$\displaystyle \lim_{x→1} \;(2x+1)=3$.

Suluhisho

Hebu$ε>0$.

Sehemu ya kwanza ya ufafanuzi huanza “Kwa kila$ε>0$.” Hii ina maana ni lazima kuthibitisha kwamba chochote kinachofuata ni kweli bila kujali thamani chanya ya$ε$ ni kuchaguliwa. Kwa kusema “Hebu$ε>0$,” tunaashiria nia yetu ya kufanya hivyo.

Chagua$δ=\frac{ε}{2}$.

ufafanuzi inaendelea na “kuna lipo$δ>0$.” maneno “kuna” katika taarifa ya hisabati daima ishara kwa mla mzoga kuwinda. Kwa maneno mengine, ni lazima tuende na kupata$δ$. Kwa hiyo, wapi hasa$δ=ε/2$ walitoka? Kuna njia mbili za msingi za kufuatilia chini$δ$. Njia moja ni algebraic tu na nyingine ni kijiometri.

Tunaanza kwa kukabiliana na tatizo kutoka kwa mtazamo wa algebraic. Tangu hatimaye tunataka$|(2x+1)−3|<ε$, tunaanza kwa kuendesha maneno haya:$|(2x+1)−3|<ε$ ni sawa na$|2x−2|<ε$, ambayo kwa upande ni sawa na$|2||x−1|<ε$. Mwisho, hii ni sawa na$|x−1|<ε/2$. Hivyo, inaonekana kwamba$δ=ε/2$ ni sahihi.

Tunaweza pia kupata$δ$ njia za kijiometri. Kielelezo$\PageIndex{2}$ kinaonyesha jinsi hii inafanyika.

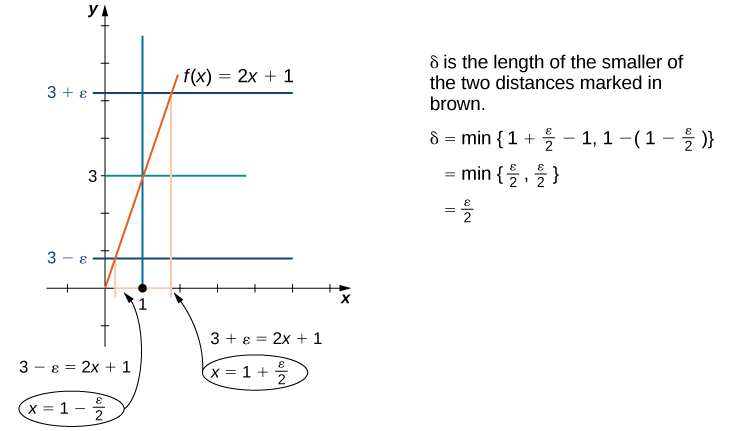
Grafu ya F ya X ni sawa na 2 X pamoja na 1, mstari wa moja kwa moja unaoongezeka kutoka asili upande wa kushoto kupitia Y ni sawa na 3 bala epsilon, Y ni sawa na 3, na Y ni sawa na 3 pamoja na epsilon. Chini ya Y ni sawa na 3, X sawa na 1; chini ya 3 bala epsilon, X ni 1 bala epsilon imegawanywa na 2; chini ya 3 pamoja na epsilon, X ni 1 pamoja na epsilon imegawanywa na 2. — Kielelezo$\PageIndex{2}$: Grafu hii inaonyesha jinsi tunavyopata$δ$ kijiometri.

Fikiria$0<|x−1|<δ$. Wakati$δ$ umechaguliwa, lengo letu ni kuonyesha kwamba ikiwa$0<|x−1|<δ$, basi$|(2x+1)−3|<ε$. Ili kuthibitisha taarifa yoyote ya fomu “Kama hii, basi hiyo,” tunaanza kwa kuchukua “hii” na kujaribu kupata “hiyo.”

Hivyo,

$|(2x+1)−3|=|2x−2|$mali ya thamani kamili

$=|2(x−1)|$

$=|2||x−1|$$|2|=2$

$=2|x−1|$

$<2⋅δ $hapa ndipo tunatumia dhana kwamba$0<|x−1|<δ$

$=2⋅\frac{ε}{2}=ε$hapa ndipo tunatumia uchaguzi wetu wa$δ=ε/2$

Uchambuzi

Katika sehemu hii ya ushahidi, tulianza$|(2x+1)−3|$ na na kutumia dhana yetu$0<|x−1|<δ$ katika sehemu muhimu ya mlolongo wa kutofautiana$|(2x+1)−3|$ ili kupata kuwa chini ya ε. Tunaweza tu kwa urahisi kuwa manipulated kukosekana kwa usawa$0<|x−1|<δ$ kudhani kufika$|(2x+1)−3|<ε$ kama ifuatavyo:

$0<|x−1|<δ⇒|x−1|<δ$

$⇒−δ<x−1<δ$

$⇒−\frac{ε}{2}<x−1<\frac{ε}{2}$

$⇒−ε<2x−2<ε$

$⇒|2x−2|<ε$

$⇒|(2x+1)−3|<ε.$

Kwa hiyo,$\displaystyle \lim_{x→1} \;(2x+1)=3.$ (Baada ya kukamilisha ushahidi, tunasema tuliyo yatimiza.)

Baada ya kuondoa maneno yote, hapa ni toleo la mwisho la ushahidi:

Hebu$ε>0$.

Chagua$δ=ε/2$.

Fikiria$0<|x−1|<δ$.

Hivyo,

\ (kuanza {align*} | (2x+1) -3| &= |2x-2|\\ [4pt]
&=|2 (x-1) |\\ [4pt]
&=|2||x-1|\\ [4pt]
&=2|x-1 |\\ [4pt]
& <2δ\\ [4pt]
&=2\ fra c {ε} {2}\\ [4pt]
&=ε. \ mwisho {align*}\)

Kwa hiyo,$\displaystyle \lim_{x→1} \;(2x+1)=3$.

Mkakati unaofuata wa kutatua matatizo hufupisha aina ya ushahidi tuliyofanya kazi katika Mfano$\PageIndex{1}$.

Kutatua matatizo Mkakati: Kuthibitisha Hiyo$\displaystyle \lim_{x→a}f(x)=L$ for a Specific Function $f(x)$

Hebu tuanze ushahidi na kauli ifuatayo: Hebu$ε>0$.
Kisha, tunahitaji kupata thamani$δ$. Baada ya kupata thamani hii, tunafanya kauli ifuatayo, kujaza tupu na uchaguzi wetu wa$δ$: Chagua$δ=$ _______.
Taarifa inayofuata katika ushahidi inapaswa kuwa (kwa hatua hii, tunajaza thamani yetu iliyotolewa$a$): Fikiria$0<|x−a|<δ$.
Kisha, kulingana na dhana hii, tunahitaji kuonyesha kwamba$|f(x)−L|<ε$, wapi$f(x)$ na$L$ ni kazi yetu$f(x)$ na kikomo chetu$L$. Kwa wakati fulani, tunahitaji kutumia$0<|x−a|<δ$.
Tunahitimisha ushahidi wetu na kauli: Kwa hiyo,$\displaystyle \lim_{x→a}f(x)=L$.

Mfano$\PageIndex{2}$: Proving a Statement about a Limit

Jaza ushahidi kwamba$\displaystyle \lim_{x→−1}\;(4x+1)=−3$ kwa kujaza vifungo.

Hebu _____.

Chagua$δ=$ _______.

$0<|x$Fikiria -_______|$<δ$.

Hivyo, |________—________|=_____________________________________$ε$.

Suluhisho

Tunaanza kwa kujaza vifungo ambapo uchaguzi umeelezwa na ufafanuzi. Hivyo, tuna

Hebu$ε>0$.

Chagua$δ$ =_______.

Fikiria$0<|x−(−1)|<δ$. (au sawa,$0<|x+1|<δ$.)

Hivyo,$|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ$ _______$ε$.

Kuzingatia mstari wa mwisho wa ushahidi, tunaona kwamba tunapaswa kuchagua$δ=\frac{ε}{4}$.

Sasa tunakamilisha kuandika mwisho wa ushahidi:

Hebu$ε>0$.

Chagua$δ=\frac{ε}{4}$.

$0<|x−(−1)|<δ$Kudhani (au sawa,$0<|x+1|<δ$.)

Hivyo,$|(4x+1)−(−3)|=|4x+4|=|4||x+1|<4δ=4(ε/4)=ε$.

Zoezi$\PageIndex{1}$

Jaza ushahidi kwamba$\displaystyle \lim_{x→2}\;(3x−2)=4$ kwa kujaza vifungo.

Hebu _______.

Chagua$δ$ =_______.

$0<|x−$Kudhani ____$|<$ ____.

Hivyo,

|___________|$=$ ______________________________$ε$.

Kwa hiyo,$\displaystyle \lim_{x→2}\;(3x−2)=4$.

Kidokezo: Fuata muhtasari katika Mkakati wa Kutatua Matatizo ambayo tumefanya kazi kwa ukamilifu katika Mfano$\PageIndex{2}$.

Jibu

Hebu$ε>0$; chagua$δ=\frac{ε}{3}$; kudhani$0<|x−2|<δ$.

Hivyo,$|(3x−2)−4|=|3x−6|=|3|⋅|x−2|<3⋅δ=3⋅(ε/3)=ε$.

Kwa hiyo,$\displaystyle \lim_{x→2}(3x−2)=4$.

Katika Mifano$\PageIndex{1}$ na$\PageIndex{2}$, ushahidi walikuwa haki moja kwa moja, tangu kazi ambayo sisi walikuwa kazi walikuwa linear. Katika Mfano$\PageIndex{3}$, tunaona jinsi ya kurekebisha ushahidi wa kubeba kazi isiyo ya kawaida.

Mfano$\PageIndex{3}$: Proving a Statement about the Limit of a Specific Function (Geometric Approach)

Thibitisha kwamba$\displaystyle \lim_{x→2}x^2=4$.

Suluhisho

1. Hebu$ε>0$. Sehemu ya kwanza ya ufafanuzi huanza “Kwa kila$ε>0$,” hivyo ni lazima tuhakikishe kwamba chochote kinachofuata ni kweli bila kujali thamani nzuri ya$ε$ huchaguliwa. Kwa kusema “Hebu$ε>0$,” tunaashiria nia yetu ya kufanya hivyo.

2. Bila kupoteza kwa ujumla, kudhani$ε≤4$. Maswali mawili yanajionyesha: Kwa nini tunataka$ε≤4$ na kwa nini ni sawa kufanya dhana hii? Kwa kujibu swali la kwanza: Baadaye, katika mchakato wa kutatua$δ$, tutagundua kwamba$δ$ inahusisha wingi$\sqrt{4−ε}$. Kwa hiyo, tunahitaji$ε≤4$. Kwa kujibu swali la pili: Ikiwa tunaweza kupata$δ>0$ hiyo “inafanya kazi” kwa$ε≤4$, basi “itafanya kazi” kwa yeyote$ε>4$ pia. Kumbuka kwamba, ingawa daima ni sawa kuweka juu amefungwa juu ε, ni kamwe sawa kuweka chini amefungwa (zaidi ya sifuri) juu$ε$.

3. Chagua$δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}$. Kielelezo$\PageIndex{3}$ inaonyesha jinsi sisi alifanya uchaguzi huu wa$δ$.

Grafu hii inaonyesha jinsi ya kupata delta kijiometri kwa epsilon kupewa kwa ushahidi hapo juu. Kwanza, kazi f (x) = x ^ 2 hutolewa kutoka [-1, 3]. Katika mhimili y, kikomo kilichopendekezwa 4 kinawekwa alama, na mstari y = 4 hutolewa kuingiliana na kazi katika (2,4). Kwa epsiloni iliyotolewa, hatua 4 + epsilon na 4 — epsiloni ni alama kwenye mhimili y juu na chini ya 4. Mstari wa rangi ya bluu hutolewa kutoka kwa pointi hizi ili kuingiliana na kazi, ambapo mistari ya pink hutolewa kutoka hatua ya makutano hadi kwenye mhimili wa x. Mstari huu unasimama upande wowote wa x=2. Kisha, tunatatua maadili haya x, ambayo yanapaswa kuwa chanya hapa. Ya kwanza ni x ^ 2 = 4 - epsilon, ambayo simplifies kwa x = sqrt (4-epsilon). Ya pili ni x^ 2 = 4 + epsilon, ambayo simplifies kwa x = sqrt (4 + epsilon). Delta ni ndogo ya umbali mbili, hivyo ni min ya (2 — sqrt (4 — epsilon) na sqrt (4 + epsilon) — 2). — Kielelezo$\PageIndex{3}$: Grafu hii inaonyesha jinsi tunavyopata δ kijiometri kwa ε iliyotolewa kwa ushahidi katika Mfano$\PageIndex{3}$.

4. Ni lazima kuonyesha: Kama$0<|x−2|<δ$, basi$|x^2−4|<ε$, hivyo ni lazima kuanza kwa kuchukua

$0<|x−2|<δ.$

Hatuhitaji kweli$0<|x−2|$ (kwa maneno mengine,$x≠2$) kwa ushahidi huu. Tangu$0<|x−2|<δ⇒|x−2|<δ$, ni sawa kushuka$0<|x−2|$.

$|x−2|<δ.$

Hivyo,

$−δ<x−2<δ.$

Kumbuka kwamba$δ=\min\{2−\sqrt{4−ε},\sqrt{4+ε}−2\}$. Hivyo,$δ≥2−\sqrt{4−ε}$ na hivyo$−(2−\sqrt{4−ε})≤−δ$. Pia tunatumia$δ≤\sqrt{4+ε}−2$ hapa. Tunaweza kuuliza katika hatua hii:$2−\sqrt{4−ε}$ Kwa$δ$ nini tulibadilisha upande wa kushoto wa usawa na$\sqrt{4+ε}−2$ upande wa kulia wa usawa? Kama sisi kuangalia Kielelezo$\PageIndex{3}$, tunaona kwamba$2−\sqrt{4−ε}$ sambamba na umbali upande wa kushoto wa$2$ juu ya$x$ -axis na$\sqrt{4+ε}−2$ inalingana na umbali upande wa kulia. Hivyo,

$−(2−\sqrt{4−ε})≤−δ<x−2<δ≤\sqrt{4+ε}−2.$

Sisi kurahisisha maneno upande wa kushoto:

$−2+\sqrt{4−ε}<x−2<\sqrt{4+ε}−2$.

Kisha, tunaongeza 2 kwa sehemu zote za usawa:

$\sqrt{4−ε}<x<\sqrt{4+ε}.$

Sisi mraba sehemu zote za usawa. Ni sawa kufanya hivyo, kwa kuwa sehemu zote za usawa ni chanya:

$4−ε<x^2<4+ε.$

Tunaondoa$4$ kutoka sehemu zote za usawa:

$−ε<x^2−4<ε.$

Mwisho,

$|x^2−4|<ε.$

5. Kwa hiyo,

$\displaystyle \lim_{x→2}x^2=4.$

Zoezi$\PageIndex{2}$

Kupata δ sambamba na$ε>0$ kwa ushahidi kwamba$\displaystyle \lim_{x→9}\sqrt{x}=3$.

Kidokezo: Chora grafu sawa na moja katika Mfano$\PageIndex{3}$.

Jibu: Chagua$δ=\text{min}\{9−(3−ε)^2,\;(3+ε)^2−9\}$.

Njia ya kijiometri ya kuthibitisha kwamba kikomo cha kazi kinachukua thamani maalum hufanya kazi vizuri kwa kazi fulani. Pia, ufahamu katika ufafanuzi rasmi wa kikomo ambacho njia hii hutoa ni muhimu sana. Hata hivyo, tunaweza pia kukabiliana na ushahidi wa kikomo kutoka kwa mtazamo wa algebraic tu. Mara nyingi, mbinu ya algebraic haiwezi tu kutupa ufahamu wa ziada katika ufafanuzi, inaweza kuwa rahisi pia. Zaidi ya hayo, mbinu ya algebraic ni chombo cha msingi kinachotumiwa katika ushahidi wa kauli kuhusu mipaka. Kwa Mfano$\PageIndex{4}$, sisi kuchukua mbinu rena algebraic.

Mfano$\PageIndex{4}$:Proving a Statement about the Limit of a Specific Function (Algebraic Approach)

Thibitisha kwamba$\displaystyle \lim_{x→−1}\;(x^2−2x+3)=6.$

Suluhisho

Hebu tutumie muhtasari wetu kutoka Mkakati wa Kutatua Matatizo:

1. Hebu$ε>0$.

2. Chagua$δ=\text{min}\{1,ε/5\}$. Uchaguzi huu wa$δ$ inaweza kuonekana isiyo ya kawaida katika mtazamo wa kwanza, lakini ilikuwa kupatikana kwa kuangalia kukosekana kwa usawa wetu mwisho taka:$∣(x^2−2x+3)−6∣<ε$. Ukosefu huu ni sawa na$|x+1|⋅|x−3|<ε$. Kwa hatua hii, jaribu tu kuchagua$δ=\frac{ε}{x−3}$ ni nguvu sana. Kwa bahati mbaya, uchaguzi wetu wa$δ$ lazima hutegemea ε tu na hakuna variable nyingine. Ikiwa tunaweza kuchukua nafasi$|x−3|$ kwa thamani ya namba, tatizo letu linaweza kutatuliwa. Hii ni mahali ambapo kuchukua$δ≤1$ anakuja katika mchezo. Uchaguzi wa$δ≤1$ hapa ni kiholela. Tunaweza kuwa tu kama urahisi kutumika yoyote idadi nyingine chanya. Katika baadhi ya ushahidi, huduma kubwa katika uchaguzi huu inaweza kuwa muhimu. Sasa, tangu$δ≤1$ na$|x+1|<δ≤1$, tuna uwezo wa kuonyesha kwamba$|x−3|<5$. Kwa hiyo,$|x+1|⋅|x−3|<|x+1|⋅5$. Katika hatua hii tunatambua kwamba tunahitaji pia$δ≤ε/5$. Hivyo, tunachagua$δ=\text{min}\{1,ε/5\}$.

3. Fikiria$0<|x+1|<δ$. Hivyo,

\[|x+1|<1\text{ and }|x+1|<\frac{ε}{5}. \nonumber \]

Tangu$|x+1|<1$, tunaweza kuhitimisha kwamba$−1<x+1<1$. Hivyo, kwa kutoa$4$ kutoka sehemu zote za usawa, tunapata$−5<x−3<−1$. Kwa hiyo,$|x−3|<5$. Hii inatupa

\[\left|(x^2−2x+3)−6\right|=|x+1|⋅|x−3|<\frac{ε}{5}⋅5=ε.\nonumber \]

Kwa hiyo,

\[\lim_{x→−1}\;(x^2−2x+3)=6.\nonumber \]

Zoezi$\PageIndex{3}$

Kukamilisha ushahidi kwamba$\displaystyle \lim_{x→1}x^2=1$.

Hebu$ε>0$; chagua$δ=\text{min}\{1,ε/3\}$; kudhani$0<|x−1|<δ$.

Tangu$|x−1|<1$, tunaweza kuhitimisha kwamba$−1<x−1<1$. Hivyo,$1<x+1<3$. Hivyo,$|x+1|<3$.

Kidokezo: Tumia Mfano$\PageIndex{4}$ kama mwongozo.

Jibu: $∣x^2−1∣=|x−1|⋅|x+1|<ε/3⋅3=ε$

Utapata kwamba, kwa ujumla, kazi ngumu zaidi, kuna uwezekano mkubwa zaidi kwamba mbinu ya algebraic ni rahisi kutumia. Njia ya algebraic pia ni muhimu zaidi katika kuthibitisha taarifa kuhusu mipaka.

Kuthibitisha Limit Sheria

Sasa tunaonyesha jinsi ya kutumia ufafanuzi wa epsilon-delta wa kikomo ili kujenga ushahidi mkali wa moja ya sheria za kikomo. Ukosefu wa usawa wa pembetatu hutumiwa katika hatua muhimu ya ushahidi, kwa hiyo tunaangalia kwanza mali hii muhimu ya thamani kamili.

Ufafanuzi: Ukosefu wa Triangle

Ukosefu wa usawa wa pembetatu unasema kwamba ikiwa$a$ na$b$ ni idadi yoyote halisi, basi$|a+b|≤|a|+|b|$.

Ushahidi

Sisi kuthibitisha zifuatazo kikomo sheria: Kama$\displaystyle \lim_{x→a}f(x)=L$ na$\displaystyle \lim_{x→a}g(x)=M$, basi$\displaystyle \lim_{x→a}\;(f(x)+g(x))=L+M$.

Hebu$ε>0$.

Chagua$δ_1>0$ ili iweze$0<|x−a|<δ_1$, basi$|f(x)−L|<ε/2$.

Chagua$δ_2>0$ ili iweze$0<|x−a|<δ_2$, basi$|g(x)−M|<ε/2$.

Chagua$δ=\text{min}\{δ_1,δ_2\}$.

Fikiria$0<|x−a|<δ$.

Hivyo,

$0<|x−a|<δ_1$na$0<|x−a|<δ_2$.

Hivyo,

\ [kuanza {align*} | (f (x) +g (x)) - (L+M) |&=| (f (x) -L) + (g (x) -M) |\\ [4pt]
&≤ |f (x) -L|+|G (x) -M|\ [4pt]
&<\ frac {ε} {2} +\ frac {2} +\ frac {2} ε} {2} =ε\ mwisho {align*}. \ nambari isiyo\]

□

Sisi sasa kuchunguza nini maana kwa kikomo si kuwepo. Kikomo$\displaystyle \lim_{x→a}f(x)$ haipo ikiwa hakuna idadi$L$ halisi ambayo$\displaystyle \lim_{x→a}f(x)=L$. Hivyo, kwa idadi zote halisi$L$,$\displaystyle \lim_{x→a}f(x)≠L$. Ili kuelewa nini hii inamaanisha, tunaangalia kila sehemu ya ufafanuzi wa$\displaystyle \lim_{x→a}f(x)=L$ pamoja na kinyume chake. Tafsiri ya ufafanuzi hutolewa katika Jedwali$\PageIndex{2}$.

Jedwali$\PageIndex{2}$. Tafsiri ya Ufafanuzi wa$\lim_{x→a}f(x)=L$ na kinyume chake
Ufafanuzi	Kinyume
1. Kwa kila$ε>0$,	1. Kuna$ε>0$ ili
2. kuna$δ>0$, ili	2. kwa kila$δ>0$,
3. ikiwa$0<\|x−a\|<δ$, basi$\|f(x)−L\|<ε$.	3. Kuna$x$ kuridhisha$0<\|x−a\|<δ$ ili$\|f(x)−L\|≥ε$.

Hatimaye, tunaweza kusema nini maana kwa kikomo si kuwepo. Kikomo$\displaystyle \lim_{x→a}f(x)$ haipo ikiwa kwa kila nambari halisi$L$, kuna idadi halisi$ε>0$ ili kwa wote$δ>0$, kuna$x$ kuridhisha$0<|x−a|<δ$, ili$|f(x)−L|≥ε$. Hebu tumia hii katika Mfano$\PageIndex{5}$ ili kuonyesha kwamba kikomo haipo.

Mfano$\PageIndex{5}$: Showing That a Limit Does Not Exist

Onyesha kwamba$\displaystyle \lim_{x→0}\frac{|x|}{x}$ haipo. Grafu ya$f(x)=|x|/x$ inavyoonekana hapa:

Grafu ya kazi na makundi mawili. Ya kwanza ipo kwa x<0, na ni mstari usio na mteremko unaoishia kwenye mhimili y katika mduara wazi kwenye (0, -1). Ya pili ipo kwa x 0, na ni mstari usio na mteremko unaoanza kwenye mhimili y katika mduara wazi (1,0)." src="https://math.libretexts.org/@api/dek...2355/2.5.3.png">

Suluhisho

Tuseme kwamba$L$ ni mgombea wa kikomo. Chagua$ε=1/2$.

Hebu$δ>0$. Aidha$L≥0$ au$L<0$. Ikiwa$L≥0$, basi basi$x=−δ/2$.

Hivyo,

$|x−0|=∣−\frac{δ}{2}−0∣=\frac{δ}{2}<δ$

$\left|\frac{∣−\frac{δ}{2}∣}{−\frac{δ}{2}}−L\right|=|−1−L|=L+1≥1>\frac{1}{2}=ε$.

Kwa upande mwingine, ikiwa$L<0$, basi basi$x=δ/2$. Hivyo,

$|x−0|=∣\frac{δ}{2}−0∣=\frac{δ}{2}<δ$

$\left|\frac{∣\frac{δ}{2}∣}{\frac{δ}{2}}−L\right|=|1−L|=|L|+1≥1>\frac{1}{2}=ε$.

Hivyo, kwa thamani yoyote ya$L$,$\displaystyle \lim_{x→0}\frac{|x|}{x}≠L.$

Mipaka ya upande mmoja

Kama vile sisi kwanza kupata uelewa angavu wa mipaka na kisha wakiongozwa na ufafanuzi ukali zaidi ya kikomo, sasa sisi upya mipaka upande mmoja. Ili kufanya hivyo, sisi kurekebisha epsilon-delta ufafanuzi wa kikomo kutoa rasmi ufafanuzi epsilon-delta kwa mipaka kutoka kulia na kushoto katika hatua. Ufafanuzi huu unahitaji tu marekebisho kidogo kutoka kwa ufafanuzi wa kikomo. Katika ufafanuzi wa kikomo kutoka haki, usawa$0<x−a<δ$ nafasi$0<|x−a|<δ$, ambayo kuhakikisha kwamba sisi tu kufikiria maadili ya$x$ kwamba ni kubwa kuliko (haki ya)$a$. Vile vile, katika ufafanuzi wa kikomo kutoka upande wa kushoto, usawa$−δ<x−a<0$ hubadilisha$0<|x−a|<δ$, ambayo inahakikisha kwamba tunazingatia tu maadili ya$x$ kwamba ni chini ya (upande wa kushoto wa)$a$.

Ufafanuzi: Mipaka ya upande mmoja (Rasmi)

Limit kutoka Haki: Hebu$f(x)$ kuelezwa juu ya muda wazi wa fomu$(a,b)$ ambapo$a<b$. Kisha

\[\lim_{x→a^+}f(x)=L \nonumber \]

kama kwa kila$ε>0$, kuna$δ>0$, kama kwamba kama$0<x−a<δ$, basi$|f(x)−L|<ε$.

Limit kutoka kushoto: Hebu$f(x)$ kuelezwa juu ya muda wazi wa fomu$(b,c)$ ambapo$b<c$. Kisha,

\[\lim_{x→c^−}f(x)=L \nonumber \]

kama kwa kila$ε>0$, kuna$δ>0$ vile kwamba kama$ −δ<x−c<0$, basi$|f(x)−L|<ε$.

Mfano$\PageIndex{6}$: Proving a Statement about a Limit From the Right

Thibitisha kwamba

\[\lim_{x→4^+}\sqrt{x−4}=0.\nonumber \]

Suluhisho

Hebu$ε>0$.

Chagua$δ=ε^2$. Tangu hatimaye tunataka$∣\sqrt{x−4}−0∣<ε$, tunaendesha usawa huu kupata$\sqrt{x−4}<ε$ au, sawa$0<x−4<ε^2$, kufanya$δ=ε^2$ uchaguzi wazi. Tunaweza pia kuamua$δ$ kijiometri, kama inavyoonekana katika Kielelezo$\PageIndex{4}$.

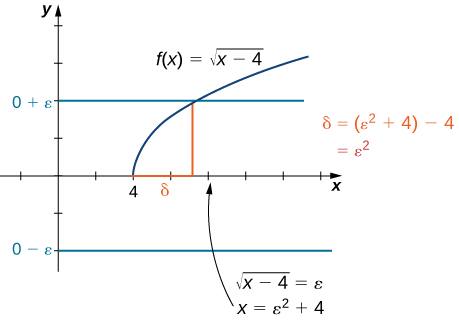
Grafu ya nusu ya juu ya usawa parabola ufunguzi wa kulia, na kilele juu ya X mhimili katika X sawa 4. Mstari Y ni sawa na 0 pamoja na epsilon pia umeonyeshwa, kuingiliana na parabola. Mstari wa wima hutoka kutoka kwenye makutano hadi kwenye mhimili wa X, kufikia mhimili kwenye X sawa na epsilon squared pamoja na 4. Umbali kutoka mahali hapo hadi 4 umeandikwa delta, na ni sawa na epsilon squared. — Kielelezo$\PageIndex{4}$: Grafu hii inaonyesha jinsi tunavyopata δ kwa ushahidi katika Mfano$\PageIndex{6}$.

Fikiria$0<x−4<δ$. Hivyo,$0<x−4<ε^2$. Hivyo,$0<\sqrt{x−4}<ε$. Hatimaye,$\left|\sqrt{x−4}−0\right|<ε$. Kwa hiyo,$\displaystyle \lim_{x→4^+}\sqrt{x−4}=0$.

Zoezi$\PageIndex{4}$

Kupata$δ$ sambamba na$ε$ kwa ushahidi kwamba$\displaystyle \lim_{x→1^−}\sqrt{1−x}=0$.

Kidokezo: Mchoro grafu na kutumia Mfano$\PageIndex{6}$ kama mwongozo wa kutatua.

Jibu: $δ=ε^2$

mipaka usio

Tunahitimisha mchakato wa kubadili mawazo yetu ya angavu ya aina mbalimbali za mipaka kwa ufafanuzi rasmi kwa kufuata ufafanuzi rasmi wa mipaka isiyo na mwisho. Kuwa na$\displaystyle \lim_{x→a}f(x)=+∞$, tunataka maadili ya kazi ya$f(x)$ kupata kubwa na kubwa kama$x$ mbinu$a$. Badala ya mahitaji ambayo$|f(x)−L|<ε$ kwa kiholela ndogo$ε$ wakati wa$0<|x−a|<δ$ kutosha$δ$, tunataka$f(x)>M$ kwa chanya kikubwa kiholela$M$ wakati wa$0<|x−a|<δ$ kutosha$δ$. Kielelezo$\PageIndex{5}$ unaeleza wazo hili kwa kuonyesha thamani ya$δ$ kwa maadili mfululizo kubwa ya$M$.

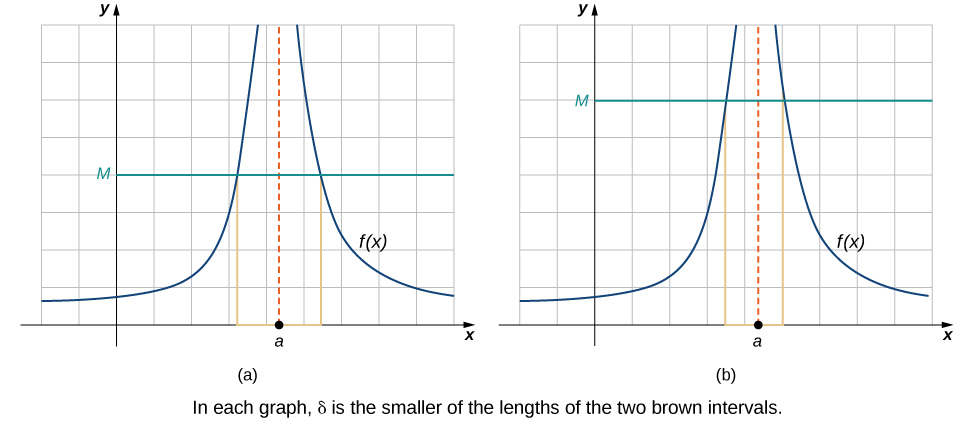
$Grafu mbili kwa upande. Kila graph ina curves mbili juu mhimili x kutengwa na asymptote katika x =a. curves upande wa kushoto kwenda infinity kama x inakwenda na 0 kama x inakwenda infinity hasi. curves juu ya haki kwenda infinity kama x inakwenda na 0 kama x inakwenda infinity. Grafu ya kwanza ina thamani M kubwa kuliko sifuri iliyowekwa kwenye mhimili y na mstari usio na usawa inayotolewa kutoka huko (y=m) ili kuingiliana na curves zote mbili. Mistari hutolewa kutoka kwenye pointi za makutano hadi kwenye mhimili wa x. Delta ni ndogo ya umbali kati ya uhakika a na matangazo haya mapya kwenye mhimili x. Mstari huo hutolewa kwenye grafu ya pili, lakini M hii ni kubwa, na umbali kutoka kwenye makutano ya mhimili x hadi kumweka ni ndogo.$

Kielelezo$\PageIndex{5}$: Hizi grafu njama maadili ya$δ$$M$ kwa kuonyesha kwamba$\displaystyle \lim_{x→a}f(x)=+∞$.

ufafanuzi: Mipaka usio (rasmi)

Hebu$f(x)$ be defined for all $x≠a$ in an open interval containing $a$. Then, we have an infinite limit

\[\lim_{x→a}f(x)=+∞ \nonumber \]

ikiwa kwa kila$M>0$, there exists $δ>0$ such that if $0<|x−a|<δ$, then $f(x)>M$.

Hebu$f(x)$ be defined for all $x≠a$ in an open interval containing $a$. Then, we have a negative infinite limit

\[\lim_{x→a}f(x)=−∞ \nonumber \]

ikiwa kwa kila$M>0$, there exists $δ>0$ such that if $0<|x−a|<δ$, then $f(x)<−M$.

Mfano$\PageIndex{7}$: Proving a Statement about an Infinite Limit

Thibitisha kwamba$\displaystyle \lim_{x→3}\frac{1}{(x-3)^2}=\infty.$

Suluhisho

Tunatumia mbinu sawa na Mkakati wetu wa awali wa kutatua matatizo. Sisi kwanza kupata sahihi$δ>0$. Kisha tunaandika ushahidi wetu.

Hatua ya 1: Kwanza tunapata sahihi$δ>0$.

1. Hebu$M$ kuwa na idadi yoyote halisi kama hiyo$M>0$.

2. Hebu$f(x) = \dfrac{1}{(x-3)^2} > M$. Kisha sisi kutatua kwa maneno$x - 3$.

Kuzidisha pande zote mbili za usawa kwa kiasi chanya$(x - 3)^2$ na kugawanya pande zote mbili kwa kiasi chanya$M$ inatupa:

\[ \frac{1}{M} > (x-3)^2 \nonumber \]

Kuchukua mizizi ya mraba ya pande zote mbili, tuna,

\[ \sqrt{\frac{1}{M}} > |x - 3|. \qquad \quad\left(\text{Remember that }\sqrt{x^2} = |x|.\right)\nonumber \]

Kuandika upya kauli hii inatupa,$0 < |x-3| < \sqrt{\dfrac{1}{M}}$. Kutoka hili tunachagua$δ = \sqrt{\dfrac{1}{M}}$.

Hatua ya 2: Sasa tunaandika ushahidi.

3. Hebu$δ = \sqrt{\dfrac{1}{M}}$ na kudhani$0 < |x-3| < δ = \sqrt{\dfrac{1}{M}}$.

Hivyo,

\[ |x-3| < \sqrt{\frac{1}{M}}. \nonumber \]

Squaring pande zote mbili inatupa,

\[ (x-3)^2 < \frac{1}{M}. \nonumber \]

Kuchukua usawa wa pande zote mbili (na kukumbuka kwamba hii itabadilisha mwelekeo wa usawa),

\[ \dfrac{1}{(x-3)^2} > M. \nonumber \]

Kwa hiyo, tuna kuthibitisha kwamba

\[\lim_{x→3}\frac{1}{(x-3)^2}=\infty.\nonumber \]

Ushahidi sawa utahitajika kwa kikomo ambacho ni sawa na$-\infty$.

Kumbuka kuwa mbinu moja ya kikomo mara nyingi inahitaji kuchukuliwa na aina hii ya kikomo. Kwa mfano, kuthibitisha:$\displaystyle \lim_{x\to 0^+}\frac{1}{x} = \infty$.

Dhana muhimu

Dhana angavu ya kikomo inaweza kuwa waongofu katika ukali hisabati ufafanuzi inayojulikana kama ufafanuzi epsilon-delta ya kikomo.
Ufafanuzi wa epsilon-delta unaweza kutumika kuthibitisha kauli kuhusu mipaka.
Ufafanuzi wa epsilon-delta wa kikomo unaweza kubadilishwa ili kufafanua mipaka ya upande mmoja.
Ufafanuzi sawa wa kikomo usio na kipimo unaweza kutumika kuthibitisha taarifa kuhusu mipaka isiyo na kipimo.

faharasa

ufafanuzi wa epsilon-delta wa kikomo: $\displaystyle \lim_{x→a}f(x)=L$kama kwa kila$ε>0$, kuna$δ>0$ vile kwamba kama$0<|x−a|<δ$, basi$|f(x)−L|<ε$

pembetatu usawa: Kama$a$ na$b$ ni idadi yoyote halisi, basi$|a+b|≤|a|+|b|$

ufafanuzi rasmi wa kikomo usio: $\displaystyle \lim_{x→a}f(x)=\infty$ikiwa kwa kila$M>0$, kuna$δ>0$ vile vile kama$0<|x−a|<δ$, basi$f(x)>M$
$\displaystyle \lim_{x→a}f(x)=-\infty$ ikiwa kwa kila$M>0$, kuna$δ>0$ vile vile kama$0<|x−a|<δ$, basi$f(x)<-M$

Wachangiaji na Majina

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College), added Example $\PageIndex{7}$ and entries for infinite limits under Key Concepts and the Glossary.

Ufafanuzi	Tafsiri
1. Kwa kila\(ε>0\),	1. Kwa kila umbali chanya\(ε\) kutoka\(L\),
2. kuna\(δ>0\),	2. Kuna umbali chanya\(δ\) kutoka\(a\),
3. vile	3. vile
4. ikiwa\(0<\|x−a\|<δ\), basi\(\|f(x)−L\|<ε\).	4. ikiwa\(x\) ni\(δ\) karibu kuliko\(a\) na\(x≠a\), basi\(f(x)\) ni\(ε\) karibu kuliko\(L\).

Ufafanuzi	Kinyume
1. Kwa kila\(ε>0\),	1. Kuna\(ε>0\) ili
2. kuna\(δ>0\), ili	2. kwa kila\(δ>0\),
3. ikiwa\(0<\|x−a\|<δ\), basi\(\|f(x)−L\|<ε\).	3. Kuna\(x\) kuridhisha\(0<\|x−a\|<δ\) ili\(\|f(x)−L\|≥ε\).

Ufafanuzi: Mipaka ya mwisho (rasmi)

Kumbuka

Mfano\(\PageIndex{1}\): Proving a Statement about the Limit of a Specific Function

Suluhisho

Kutatua matatizo Mkakati: Kuthibitisha Hiyo\(\displaystyle \lim_{x→a}f(x)=L\) for a Specific Function \(f(x)\)

Mfano\(\PageIndex{2}\): Proving a Statement about a Limit

Suluhisho

Zoezi\(\PageIndex{1}\)

Mfano\(\PageIndex{3}\): Proving a Statement about the Limit of a Specific Function (Geometric Approach)

Suluhisho

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{4}\):Proving a Statement about the Limit of a Specific Function (Algebraic Approach)

Suluhisho

Zoezi\(\PageIndex{3}\)

Ufafanuzi: Ukosefu wa Triangle

Ushahidi

Mfano\(\PageIndex{5}\): Showing That a Limit Does Not Exist

Suluhisho

Ufafanuzi: Mipaka ya upande mmoja (Rasmi)

Mfano\(\PageIndex{6}\): Proving a Statement about a Limit From the Right

Suluhisho

Zoezi\(\PageIndex{4}\)

ufafanuzi: Mipaka usio (rasmi)

Mfano\(\PageIndex{7}\): Proving a Statement about an Infinite Limit

Suluhisho