2.5E: Mazoezi ya Sehemu ya 2.5

Last updated
Save as PDF

Page ID: 178961

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Katika mazoezi ya 1 - 4, weka$ ε − δ$ ufafanuzi sahihi kwa kila taarifa zilizotolewa.

1)$\displaystyle \lim_{x →a}f(x)=N$

2)$\displaystyle \lim_{t →b}g(t)=M$

Jibu: Kwa kila$ ε >0$, kuna$ δ >0$, ili kama$0 <|t −b| < δ$, basi$|g(t) −M| < ε$

3)$\displaystyle \lim_{x →c}h(x)=L$

4)$\displaystyle \lim_{x →a} φ(x)=A$

Jibu: Kwa kila$ ε >0$, kuna$ δ >0$, ili kama$0 <|x −a| < δ$, basi$| φ(x) −A| < ε$

Grafu inayofuata ya kazi$f$ inatimiza$\displaystyle \lim_{x →2}f(x)=2$. Katika mazoezi yafuatayo, onyesha thamani ya$ δ >0$ kwamba satisfies kila taarifa.

kazi inayotolewa katika roboduara moja kwa x 0. Ni kuongezeka concave up kazi, na pointi takriban (0,0), (1, .5), (2,2), na (3,4)." style="width: 417px; height: 422px;" width="417px" height="422px" src="https://math.libretexts.org/@api/dek...02_05_204.jpeg">

5) Ikiwa$0 <|x −2| < δ$, basi$|f(x) −2| <1$.

6) Ikiwa$0 <|x −2| < δ$, basi$|f(x) −2| <0.5$.

Jibu: $ δ ≤0.25$

Grafu inayofuata ya kazi$f$ inatimiza$\displaystyle \lim_{x →3}f(x)= −1$. Katika mazoezi yafuatayo, onyesha thamani ya$ δ >0$ kwamba satisfies kila taarifa.

Grafu ya kazi ya kupungua kwa mstari, na pointi (0,2), (1,1), (2,0), (3, -1), (4, -2), na kadhalika kwa x = 0." style="width: 417px; height: 422px;" width="417px" height="422px" src="https://math.libretexts.org/@api/dek...02_05_205.jpeg">

7) Ikiwa$0 <|x −3| < δ$, basi$|f(x)+1| <1$.

8) Ikiwa$0 <|x −3| < δ$, basi$|f(x)+1| <2$.

Jibu: $ δ ≤2$

Grafu inayofuata ya kazi$f$ inatimiza$\displaystyle \lim_{x →3}f(x)=2$. Katika mazoezi yafuatayo, kwa kila thamani ya$ ε$, kupata thamani ya$ δ >0$ vile kwamba ufafanuzi sahihi wa kikomo ana kweli.

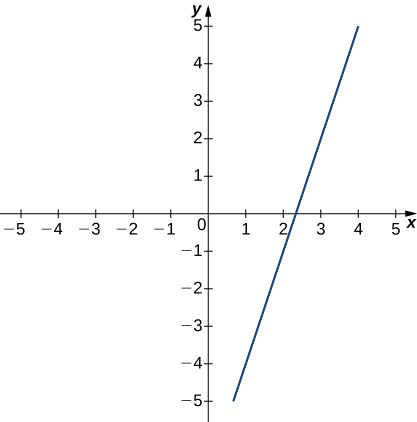
$Grafu ya kazi inayoongezeka ya mstari inayoingiliana na mhimili x karibu (2.25, 0) na kupitia pointi (3,2) na, takriban, (1, -5) na (4,5).$

9)$ ε=1.5$

10)$ ε=3$

Jibu: $ δ ≤1$

[T] Katika mazoezi 11 - 12, tumia calculator ya graphing ili kupata idadi kama$ δ$ vile taarifa zinashikilia kweli.

11)$\left|\sin(2x) −\frac{1}{2}\right| <0.1$, wakati wowote$\left|x −\frac{ π}{12}\right| < δ$

12)$\left|\sqrt{x −4} −2\right| <0.1$, wakati wowote$|x −8| < δ$

Jibu: $ δ <0.3900$

Katika mazoezi 13 - 17, tumia ufafanuzi sahihi wa kikomo ili kuthibitisha mipaka iliyotolewa.

13)$\displaystyle \lim_{x →2}\,(5x+8)=18$

14)$\displaystyle \lim_{x →3}\frac{x^2 −9}{x −3}=6$

Jibu: Hebu$ δ= ε$. Ikiwa$0 <|x −3| < ε$, basi$\left|\dfrac{x^2 −9}{x −3} - 6\right| = \left|\dfrac{(x+3)(x −3)}{x −3} - 6\right| = |x+3 −6|=|x −3| < ε$.

15)$\displaystyle \lim_{x →2}\frac{2x^2 −3x −2}{x −2}=5$

16)$\displaystyle \lim_{x →0}x^4=0$

Jibu: Hebu$ δ=\sqrt[4]{ ε}$. Ikiwa$0 <|x| <\sqrt[4]{ ε}$, basi$\left|x^4-0\right|=x^4 < ε$.

17)$\displaystyle \lim_{x →2}\,(x^2+2x)=8$

Katika mazoezi 18 - 20, tumia ufafanuzi sahihi wa kikomo ili kuthibitisha mipaka iliyopewa upande mmoja.

18)$\displaystyle \lim_{x →5^ −}\sqrt{5 −x}=0$

Jibu: Hebu$ δ= ε^2$. Kama$- ε^2 < x - 5 < 0,$ tunaweza kuzidisha$-1$ kwa njia ya kupata$0 <5-x < ε^2.$
Kisha$\left|\sqrt{5 −x} - 0\right|=\sqrt{5 −x} < \sqrt{ ε^2} = ε$.

19)$\displaystyle \lim_{x →0^+}f(x)= −2$, wapi$f(x)=\begin{cases}8x −3, & \text{if }x <0\\4x −2, & \text{if }x ≥0\end{cases}$.

20)$\displaystyle \lim_{x →1^ −}f(x)=3$, wapi$f(x)=\begin{cases}5x −2, & \text{if }x <1\\7x −1, & \text{if }x ≥1\end{cases}$.

Jibu: Hebu$ δ= ε/5$. Kama$ − ε/5 < x - 1 <0,$ tunaweza kuzidisha$-1$ kwa njia ya kupata$0 <1-x < ε/5.$
Kisha$|f(x) −3|=|5x-2-3| = |5x −5| = 5(1-x),$ tangu$x <1$ hapa.
Na$5(1-x) < 5( ε/5) = ε$.

Katika mazoezi 21 - 23, tumia ufafanuzi sahihi wa kikomo ili kuthibitisha mipaka iliyopewa usio na kipimo.

21)$\displaystyle \lim_{x →0}\frac{1}{x^2}= ∞$

22)$\displaystyle \lim_{x → −1}\frac{3}{(x+1)^2}= ∞$

Jibu: Hebu$ δ=\sqrt{\frac{3}{N}}$. Ikiwa$0 <|x+1| <\sqrt{\frac{3}{N}}$, basi$f(x)=\frac{3}{(x+1)^2} >N$.

23)$\displaystyle \lim_{x →2} −\frac{1}{(x −2)^2}= − ∞$

24) Mhandisi anatumia mashine ya kukata mraba gorofa ya Aerogel ya eneo hilo$144 \,\text{cm}^2$. Kama kuna upeo wa makosa kuvumiliana katika eneo la$8 \,\text{cm}^2$, jinsi usahihi lazima mhandisi kukata upande, kuchukua pande zote na urefu sawa? Nambari hizi$ δ$ zinahusianaje na$ ε$$a$,, na$L$?

Jibu: $0.033 \text{ cm}, \, ε=8,\, δ=0.33,\,a=12,\,L=144$

25) Tumia ufafanuzi sahihi wa kikomo ili kuthibitisha kwamba kikomo kinachofuata haipo:$\displaystyle \lim_{x →1}\frac{|x −1|}{x −1}.$

26) Kutumia ufafanuzi sahihi wa mipaka, kuthibitisha kwamba$\displaystyle \lim_{x →0}f(x)$ haipo, kutokana na kwamba$f(x)$ ni kazi dari. (kidokezo: Jaribu yoyote$ δ <1$.)

Jibu: Majibu inaweza sana.

27) Kutumia ufafanuzi sahihi wa mipaka, kuthibitisha kwamba$\displaystyle \lim_{x →0}f(x)$ haipo:$f(x)=\begin{cases}1, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Kidokezo: Fikiria jinsi unaweza daima kuchagua idadi ya busara$0 <d$, >

28) Kwa kutumia ufafanuzi sahihi wa mipaka, kuamua$\displaystyle \lim_{x →0}f(x)$ kwa$f(x)=\begin{cases}x, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Kidokezo: Kuvunja katika kesi mbili,$x$ busara na$x$ irrational.)

Jibu: $0$

29) Kutumia kazi kutoka kwa zoezi la awali, tumia ufafanuzi sahihi wa mipaka ili kuonyesha kwamba$\displaystyle \lim_{x →a}f(x)$ haipo$a ≠0$

Kwa mazoezi 30 - 32, tuseme kwamba$\displaystyle \lim_{x →a}f(x)=L$ na$\displaystyle \lim_{x →a}g(x)=M$ zote mbili zipo. Tumia ufafanuzi sahihi wa mipaka ili kuthibitisha sheria zifuatazo za kikomo:

30)$\displaystyle \lim_{x →a}(f(x) −g(x))=L −M$

Jibu: $f(x) −g(x)=f(x)+( −1)g(x)$

31)$\displaystyle \lim_{x →a}[cf(x)]=cL$ kwa mara yoyote halisi$c$ (dokezo: Fikiria kesi mbili:$c=0$ na$c ≠0$.)

32)$\displaystyle \lim_{x →a}[f(x)g(x)]=LM$. (Kidokezo:$|f(x)g(x) −LM|= |f(x)g(x) −f(x)M +f(x)M −LM| ≤|f(x)||g(x) −M| +|M||f(x) −L|.)$

Jibu: Majibu yanaweza kutofautiana.