2.4: Kuendelea

Malengo ya kujifunza

• Eleza masharti matatu ya mwendelezo katika hatua.
• Eleza aina tatu za discontinuities.
• Eleza mwendelezo juu ya muda.
• Weka theorem kwa mipaka ya kazi za composite.
• Kutoa mfano wa theorem ya thamani ya kati.

Kazi nyingi zina mali ambayo grafu zao zinaweza kufuatiliwa na penseli bila kuinua penseli kutoka ukurasa. Kazi hizo zinaitwa kuendelea. Kazi nyingine zina pointi ambazo mapumziko katika grafu hutokea, lakini kukidhi mali hii kwa vipindi vilivyomo katika vikoa vyao. Wao ni kuendelea juu ya vipindi hivi na inasemekana kuwa na discontinuity katika hatua ambapo mapumziko hutokea.

Tunaanza uchunguzi wetu wa mwendelezo kwa kuchunguza nini maana kwa kazi ya kuwa na mwendelezo katika hatua. Intuitively, kazi inaendelea kwa hatua fulani ikiwa hakuna mapumziko katika grafu yake wakati huo.

Mwendelezo katika Point

Kabla ya kuangalia ufafanuzi rasmi wa nini maana ya kazi kuwa endelevu kwa hatua, hebu fikiria kazi mbalimbali ambazo zinashindwa kukidhi dhana yetu ya angavu ya maana ya kuendelea kwa hatua. Kisha tunaunda orodha ya hali zinazozuia kushindwa vile.

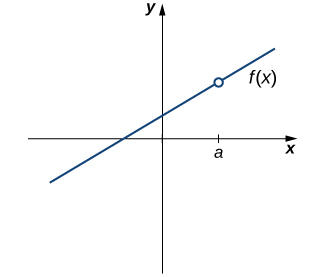
Kazi yetu ya kwanza ya maslahi inavyoonekana katika Kielelezo$\PageIndex{1}$. Tunaona kwamba grafu ya$f(x)$ ina shimo katika$a$. Kwa kweli,$f(a)$ ni undefined. Kwa uchache sana,$f(x)$ kwa kuwa kuendelea saa$a$, tunahitaji hali ifuatayo:

i.$f(a)$ hufafanuliwa

Kielelezo$\PageIndex{1}$: kazi$f(x)$ si kuendelea kwa$a$ sababu$f(a)$ ni undefined.

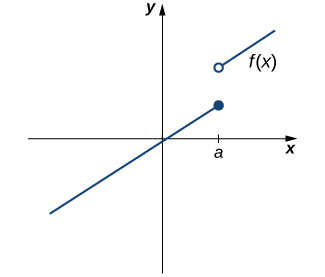
Hata hivyo, kama tunavyoona katika Kielelezo$\PageIndex{2}$, hali hii peke yake haitoshi kuhakikisha kuendelea kwa uhakika$a$. Ingawa$f(a)$ hufafanuliwa, kazi ina pengo katika$a$. Katika mfano huu, pengo lipo kwa sababu$\displaystyle \lim_{x→a}f(x)$ haipo. Ni lazima kuongeza hali nyingine kwa ajili ya mwendelezo katika$a$ -yaani,

ii. $\displaystyle \lim_{x→a}f(x)$ipo

Kielelezo$\PageIndex{2}$: kazi$f(x)$ si kuendelea kwa$a$ sababu$\displaystyle \lim_{x→a}f(x)$ haipo.

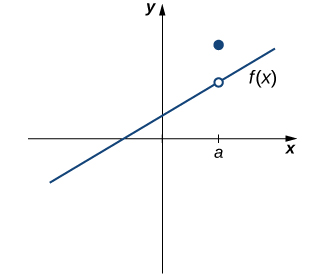
Hata hivyo, kama tunavyoona katika Kielelezo$\PageIndex{3}$, hali hizi mbili kwa wenyewe hazihakikishi kuendelea kwa hatua. Kazi katika takwimu hii inatimiza masharti yetu mawili ya kwanza, lakini bado haiendelei$a$. Lazima tuongeze hali ya tatu kwenye orodha yetu:

iii. $\displaystyle \lim_{x→a}f(x)=f(a)$

Kielelezo$\PageIndex{3}$: kazi$f(x)$ si kuendelea kwa$a$ sababu$\displaystyle \lim_{x→a}f(x)≠f(a)$.

Sasa tunaweka orodha yetu ya masharti pamoja na kuunda ufafanuzi wa kuendelea kwa hatua.

Ufafanuzi: Kuendelea katika Point

kazi$f(x)$ ni kuendelea katika hatua $a$kama na tu kama zifuatazo hali tatu ni kuridhika:

1. $f(a)$hufafanuliwa
2. $\displaystyle \lim_{x→a}f(x)$ipo
3. $\displaystyle \lim_{x→a}f(x)=f(a)$

Kazi ni discontinuous katika hatua$a$ kama inashindwa kuendelea katika$a$.

Utaratibu unaofuata unaweza kutumika kuchambua mwendelezo wa kazi kwa hatua kwa kutumia ufafanuzi huu.

Mkakati wa Kutatua Matatizo: Kuamua Kuendelea kwa Point

1. Angalia ili uone ikiwa$f(a)$ inafafanuliwa. Ikiwa$f(a)$ haijulikani, hatuhitaji kwenda zaidi. kazi si kuendelea katika$a.$ Kama$f(a)$ ni defined, kuendelea hatua 2.
2. kukokotoa$\displaystyle \lim_{x→a}f(x)$. Katika hali nyingine, tunaweza kuhitaji kufanya hivyo kwa kompyuta ya kwanza$\displaystyle \lim_{x→a^−}f(x)$ na$\displaystyle \lim_{x→a^+}f(x)$. Ikiwa$\displaystyle \lim_{x→a}f(x)$ haipo (yaani, sio namba halisi), basi kazi haiendelei$a$ na tatizo linatatuliwa. Ikiwa$\displaystyle \lim_{x→a}f(x)$ ipo, kisha endelea hatua ya 3.
3. Linganisha$f(a)$ na$\displaystyle \lim_{x→a}f(x)$. Ikiwa$\displaystyle \lim_{x→a}f(x)≠f(a)$, basi kazi haiendelei$a.$ ikiwa$\displaystyle \lim_{x→a}f(x)=f(a)$, basi kazi inaendelea$a.$

Mifano mitatu ijayo inaonyesha jinsi ya kutumia ufafanuzi huu ili kuamua kama kazi inaendelea kwa hatua fulani. Mifano hii inaonyesha hali ambayo kila hali ya kuendelea katika ufafanuzi kufanikiwa au kushindwa.

Mfano$\PageIndex{1A}$: Determining Continuity at a Point, Condition 1

Kutumia ufafanuzi, onyesha kama kazi$f(x)=\dfrac{x^2−4}{x−2}$ inaendelea$x=2$. Thibitisha hitimisho.

Suluhisho

Hebu tuanze kwa kujaribu kuhesabu$f(2)$. Tunaweza kuona kwamba$f(2)=0/0$, ambayo ni undefined. Kwa hiyo,$f(x)=\dfrac{x^2−4}{x−2}$ ni discontinuous kwa$2$ sababu$f(2)$ ni undefined. Grafu ya$f(x)$ inavyoonekana kwenye Kielelezo$\PageIndex{4}$.

Kielelezo$\PageIndex{4}$: kazi$f(x)$ ni discontinuous kwa$2$ sababu$f(2)$ ni undefined.

Mfano$\PageIndex{1B}$: Determining Continuity at a Point, Condition 2

Kutumia ufafanuzi, onyesha kama kazi$f(x)=\begin{cases}−x^2+4, & \mathrm{if} \; x≤3 \\ 4x−8, & \mathrm{if} \; x>3\end{cases}$ inaendelea$x=3$. Thibitisha hitimisho.

Suluhisho

Hebu tuanze kwa kujaribu kuhesabu$f(3)$.

$f(3)=−(3^2)+4=−5$.

Hivyo,$f(3)$ hufafanuliwa. Kisha, tunahesabu$\displaystyle \lim_{x→3}f(x)$. Ili kufanya hivyo, tunapaswa kuhesabu$\displaystyle \lim_{x→3^−}f(x)$ na$\displaystyle \lim_{x→3^+}f(x)$:

$\displaystyle \lim_{x→3^−}f(x)=−(3^2)+4=−5$

na

$\displaystyle \lim_{x→3^+}f(x)=4(3)−8=4$.

Kwa hiyo,$\displaystyle \lim_{x→3}f(x)$ haipo. Hivyo,$f(x)$ si kuendelea katika 3. Grafu ya$f(x)$ inavyoonekana kwenye Kielelezo$\PageIndex{5}$.

3. Kuna mduara wazi mwishoni mwa mstari ambapo x itakuwa 3." src="https://math.libretexts.org/@api/dek...2347/2.4.2.png">

Kielelezo$\PageIndex{5}$: kazi$f(x)$ si kuendelea katika 3 kwa sababu$\displaystyle \lim_{x→3}f(x)$ haipo.

Mfano$\PageIndex{1C}$: Determining Continuity at a Point, Condition 3

Kutumia ufafanuzi, onyesha kama kazi$f(x)=\begin{cases}\frac{\sin x}{x}, & \text{if } x≠0\\1, & \text{if } x=0\end{cases}$ inaendelea$x=0$.

Suluhisho

Kwanza, angalia kwamba

$f(0)=1$

Ifuatayo,

$\displaystyle \lim_{x→0}f(x)=\lim_{x→0}\frac{\sin x}{x}=1$.

Mwisho, kulinganisha$f(0)$ na$\displaystyle \lim_{x→0}f(x)$. Tunaona kwamba

$\displaystyle f(0)=1=\lim_{x→0}f(x)$.

Kwa kuwa zote tatu ya masharti katika ufafanuzi wa mwendelezo ni kuridhika,$f(x)$ ni kuendelea katika$x=0$.

Zoezi$\PageIndex{1}$

Kutumia ufafanuzi, onyesha kama kazi$f(x)=\begin{cases}2x+1, & \text{if }x<1\\2, & \text{if }x=1\\ −x+4, & \text{if }x>1\end{cases}$ inaendelea$x=1$. Ikiwa kazi haiendelei saa 1, onyesha hali ya kuendelea kwa hatua ambayo inashindwa kushikilia.

Kidokezo

Angalia kila hali ya ufafanuzi.

Jibu

$f$si kuendelea kwa$1$ sababu$\displaystyle f(1)=2≠3=\lim_{x→1}f(x)$.

Kwa kutumia ufafanuzi wa kuendelea na theorems zilizoanzishwa hapo awali kuhusu tathmini ya mipaka, tunaweza kusema theorem ifuatayo.

Theorem$\PageIndex{1}$: Continuity of Polynomials and Rational Functions

Polynomials na kazi za busara zinaendelea kila wakati katika vikoa vyao.

Ushahidi

Hapo awali, tulionyesha kwamba ikiwa$p(x)$ na$q(x)$ ni polynomials,$\displaystyle \lim_{x→a}p(x)=p(a)$ kwa kila polynomial$p(x)$ na kwa muda mrefu$\displaystyle \lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}$ kama$q(a)≠0$. Kwa hiyo, polynomials na kazi za busara zinaendelea kwenye vikoa vyao.

□

Sasa tunatumia Theorem$\PageIndex{1}$ kuamua pointi ambazo kazi ya busara iliyopewa inaendelea.

Mfano$\PageIndex{2}$:Continuity of a Rational Function

Kwa maadili gani ya x$f(x)=\dfrac{x+1}{x−5}$ yanaendelea?

Suluhisho

Kazi ya busara$f(x)=\dfrac{x+1}{x−5}$ inaendelea kwa kila thamani ya$x$ isipokuwa$x=5$.

Zoezi$\PageIndex{2}$

Kwa maadili gani$x$$f(x)=3x^4−4x^2$ yanaendelea?

Kidokezo

Tumia mwendelezo wa Polynomials na Kazi za busara zilizotajwa hapo juu.

Jibu

$f(x)$ni kuendelea katika kila idadi halisi.

Aina ya Discontinuities

Kama tulivyoona katika Mfano$\PageIndex{1A}$ na Mfano$\PageIndex{1B}$, discontinuities kuchukua mechi mbalimbali. Sisi kuainisha aina ya discontinuities tumeona hadi sasa kama discontinuities kutolewa, discontinuities usio, au kuruka discontinuities. Intuitively, discontinuity kutolewa ni kukomesha ambayo kuna shimo katika grafu, kuruka discontinuity - noninfinite discontinuity ambayo sehemu ya kazi si kukutana, na kutokuwepo usio - discontinuity iko katika dalili ya wima. Kielelezo$\PageIndex{6}$ unaeleza tofauti katika aina hizi za discontinuities. Ingawa maneno haya hutoa njia nzuri ya kuelezea aina tatu za kawaida za discontinuities, kukumbuka kwamba sio discontinuities zote zinafaa vizuri katika makundi haya.

0, kuna mduara wazi kwenye mstari na mduara uliofungwa vitengo vichache juu ya mstari. Ya pili ni kuacha kuruka. Hapa, kuna mistari miwili yenye mteremko mzuri. Mstari wa kwanza upo kwa x<=a, na wa pili upo kwa x>a, ambapo a> 0. Mstari wa kwanza unaishia kwenye mduara imara ambapo x=a, na pili huanza vitengo chache hadi na mduara wazi katika x=a. aina ya tatu discontinuity ni usio discontinuity. Hapa, kazi ina sehemu mbili kutengwa na asymptote x =a. sehemu ya kwanza ni Curve kunyoosha pamoja mhimili x kwa 0 kama x inakwenda infinity hasi na pamoja mhimili y infinity kama x inakwenda sifuri. Sehemu ya pili ni safu inayoelekea kando ya mhimili y hadi infinity hasi kama x inakwenda sifuri na kando ya mhimili x hadi 0 kama x inakwenda infinity." style="width: 975px; height: 315px;" width="975px" height="315px" src="https://math.libretexts.org/@api/dek...02_04_006.jpeg">

Kielelezo$\PageIndex{6}$: Discontinuities ni classified kama (a) kutolewa, (b) kuruka, au (c) usio.

Discontinuities hizi tatu hufafanuliwa rasmi kama ifuatavyo:

Ufafanuzi

Kama$f(x)$ ni discontinuous wakati$a,$ huo

1. $f$ina discontinuity removable katika$a$ kama$\displaystyle \lim_{x→a}f(x)$ ipo. (Kumbuka: Tunaposema kwamba$\displaystyle \lim_{x→a}f(x)$ ipo, tunamaanisha kwamba$\displaystyle \lim_{x→a}f(x)=L$, wapi$L$ namba halisi.)

2. $f$ina kuruka discontinuity katika$a$ kama$\displaystyle \lim_{x→a^−}f(x)$ na$\displaystyle \lim_{x→a^+}f(x)$ wote zipo, lakini$\displaystyle \lim_{x→a^−}f(x)≠lim_{x→a^+}f(x)$. (Kumbuka: Tunaposema kwamba$\displaystyle \lim_{x→a^−}f(x)$ na$\displaystyle \lim_{x→a^+}f(x)$ zote mbili zipo, tunamaanisha kwamba wote wawili ni thamani halisi na kwamba wala kuchukua maadili$±∞$.)

3. $f$ina discontinuity usio katika$a$ kama$\displaystyle \lim_{x→a^−}f(x)=±∞$ au$\displaystyle \lim_{x→a^+}f(x)=±∞$.

Mfano$\PageIndex{3}$: Classifying a Discontinuity

Katika Mfano$\PageIndex{1A},$ sisi ilionyesha kwamba$f(x)=\dfrac{x^2−4}{x−2}$ ni discontinuous katika$x=2$. Kuainisha discontinuity hii kama removable, kuruka, au usio.

Suluhisho

Ili kuainisha discontinuity katika$2$ tunapaswa kutathmini$\displaystyle \lim_{x→2}f(x)$:

\ (\ displaystyle\ kuanza {align*}\ lim_ {x → 2} f (x) &=\ lim_ {x → 2}\ frac {x ^ 2,14} {x-1 2}\\ [4pt]
&=\ lim_ {x → 2}\ frac {(x-2)} {x-1 2}\\ [4pt]
&=\ lim_ {x → 2) _ {x→ 2} (x+2)\\ [4pt]
&=4. \ mwisho {align*}\)

Tangu$f$ ni discontinuous katika$2$ na$\displaystyle \lim_{x→2}f(x)$ ipo,$f$ ina discontinuity kutolewa katika$x=2$.

Mfano$\PageIndex{4}$: Classifying a Discontinuity

Katika Mfano$\PageIndex{1B}$, sisi ilionyesha kwamba$f(x)=\begin{cases}−x^2+4, &\text{if }x≤3\\4x−8, &\text{if }x>3\end{cases}$ ni discontinuous katika$x=3$. Kuainisha discontinuity hii kama removable, kuruka, au usio.

Suluhisho

Mapema, sisi ilionyesha kuwa$f$ ni discontinuous saa$3$ kwa sababu$\displaystyle \lim_{x→3}f(x)$ haipo. Hata hivyo, tangu$\displaystyle \lim_{x→3^−}f(x)=−5$ na$\displaystyle \lim_{x→3^+}f(x)=4$ zote mbili zipo, tunahitimisha kuwa kazi ina kuacha kuruka$3$.

Mfano$\PageIndex{5}$: Classifying a Discontinuity

Kuamua kama$f(x)=\dfrac{x+2}{x+1}$ ni kuendelea katika$−1$. Kama kazi ni discontinuous katika$−1$, kuainisha discontinuity kama removable, kuruka, au usio.

Suluhisho

Thamani ya kazi$f(−1)$ haijulikani. Kwa hiyo, kazi haiendelei$−1$. Kuamua aina ya kuacha, lazima tueleze kikomo$−1$. Tunaona kwamba$\displaystyle \lim_{x→−1^−}\frac{x+2}{x+1}=−∞$ na$\displaystyle \lim_{x→−1^+}\frac{x+2}{x+1}=+∞$. Kwa hiyo, kazi ina discontinuity usio na mwisho$−1$.

Zoezi$\PageIndex{3}$

Kwa$f(x)=\begin{cases}x^2, &\text{if }x≠1\\3, & \text{if }x=1\end{cases}$, kuamua kama$f$ ni kuendelea katika$1$. Kama$f$ si kuendelea katika$1$, kuainisha discontinuity kama removable, kuruka, au usio.

Kidokezo

Fikiria ufafanuzi wa aina mbalimbali za kuacha zilizotajwa hapo juu. Kama kazi ni discontinuous katika$1$, angalia$\displaystyle \lim_{x→1}f(x)$

Jibu

Kuacha saa$1$; kutolewa

Kuendelea juu ya Muda

Sasa kwa kuwa tumechunguza dhana ya kuendelea kwa hatua, tunapanua wazo hilo kuendelea kwa muda. Tunapoendeleza wazo hili kwa aina tofauti za vipindi, inaweza kuwa na manufaa kukumbuka wazo la angavu kwamba kazi inaendelea zaidi ya muda ikiwa tunaweza kutumia penseli kufuatilia kazi kati ya pointi zozote mbili katika kipindi bila kuinua penseli kutoka kwenye karatasi. Katika maandalizi ya kufafanua mwendelezo kwa muda, tunaanza kwa kuangalia ufafanuzi wa maana ya kazi ya kuendelea kutoka kulia kwa hatua na kuendelea kutoka kushoto kwa hatua.

Ufafanuzi: Kuendelea kutoka kulia na kutoka kushoto

kazi$f(x)$ inasemekana kuendelea kutoka haki katika$a$ kama$\displaystyle \lim_{x→a^+}f(x)=f(a)$.

kazi$f(x)$ inasemekana kuendelea kutoka kushoto katika$a$ kama$\displaystyle \lim_{x→a^−}f(x)=f(a)$

Kazi inaendelea juu ya muda wa wazi ikiwa inaendelea kila wakati. Kazi$f(x)$ inaendelea juu ya muda uliofungwa wa fomu$[a,b]$ ikiwa inaendelea kila hatua$(a,b)$ na inaendelea kutoka kulia$a$ na inaendelea kutoka kushoto kwa$b.$ Analoguously, kazi$f(x)$ inaendelea kwa muda wa fomu $(a,b]$ikiwa ni kuendelea tena$(a,b)$ na inaendelea kutoka upande wa kushoto katika$b.$ Mwendelezo juu ya aina nyingine ya vipindi hufafanuliwa kwa mtindo sawa.

Inahitaji$\displaystyle \lim_{x→a^+}f(x)=f(a)$ hilo na$\displaystyle \lim_{x→b^−}f(x)=f(b)$ kuhakikisha kwamba tunaweza kufuatilia grafu ya kazi kutoka hatua$(a,f(a))$ hadi hatua$(b,f(b))$ bila kuinua penseli. Ikiwa, kwa mfano$\displaystyle \lim_{x→a^+}f(x)≠f(a)$, tunahitaji kuinua penseli yetu kuruka kutoka$f(a)$ kwenye grafu ya kazi yote juu$(a,b]$.

Mfano$\PageIndex{6}$: Continuity on an Interval

Weka muda (s) juu ya kazi ambayo$f(x)=\dfrac{x−1}{x^2+2x}$ inaendelea.

Suluhisho

Kwa kuwa$f(x)=\dfrac{x−1}{x^2+2x}$ ni kazi ya busara, inaendelea kila wakati katika uwanja wake. Domain ya$f(x)$ ni kuweka$(−∞,−2)∪(−2,0)∪(0,+∞)$. Hivyo,$f(x)$ ni kuendelea juu ya kila moja ya vipindi$(−∞,−2),(−2,0)$, na$(0,+∞)$.

Mfano$\PageIndex{7}$: Continuity over an Interval

Weka muda (s) juu ya kazi ambayo$f(x)=\sqrt{4−x^2}$ inaendelea.

Suluhisho

Kutoka sheria kikomo, tunajua kwamba$\displaystyle \lim_{x→a}\sqrt{4−x^2}=\sqrt{4−a^2}$ kwa maadili yote ya katika$(−2,2)$. Pia tunajua kwamba$\displaystyle \lim_{x→−2^+}\sqrt{4−x^2}=0$ ipo na$\displaystyle \lim_{x→2^−}\sqrt{4−x^2}=0$ ipo. Kwa hiyo,$f(x)$ ni kuendelea juu ya muda$[−2,2]$.

Zoezi$\PageIndex{4}$

Weka muda (s) juu ya kazi ambayo$f(x)=\sqrt{x+3}$ inaendelea.

Kidokezo

Tumia Mfano$\PageIndex{7}$ kama mwongozo.

Jibu

$[−3,+∞)$

Theorem$\PageIndex{2}$ inatuwezesha kupanua uwezo wetu wa kukokotoa mipaka. Hasa, theorem hii hatimaye inatuwezesha kuonyesha kwamba kazi za trigonometri zinaendelea juu ya vikoa vyao.

Theorem$\PageIndex{2}$: Composite Function Theorem

Kama$f(x)$ ni kuendelea katika$L$ na$\displaystyle \lim_{x→a}g(x)=L$, basi

$\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L).$

Kabla ya kuendelea na Mfano$\PageIndex{8},$ kukumbuka kwamba mapema, katika sehemu ya sheria kikomo, sisi ilionyesha$\displaystyle \lim_{x→0}\cos x=1=\cos(0)$. Kwa hiyo, tunajua kwamba$f(x)=\cos x$ ni kuendelea katika$0$. Katika Mfano$\PageIndex{8},$ tunaona jinsi ya kuchanganya matokeo haya na theorem ya kazi ya composite.

Mfano$\PageIndex{8}$: Limit of a Composite Cosine Function

Tathmini$\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)$.

Suluhisho

Kazi iliyotolewa ni composite ya$\cos x$ na$x−\frac{π}{2}$. Tangu$\displaystyle \lim_{x→π/2}\left(x−\frac{π}{2}\right)=0$ na$\cos x$ ni kuendelea katika$0$, tunaweza kutumia Composite kazi theorem. Hivyo,

$\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)=\cos\left(\lim_{x→π/2}\left(x−\frac{π}{2}\right)\right)=\cos(0)=1.$

Zoezi$\PageIndex{4}$:

Tathmini$\displaystyle \lim_{x→π}\sin(x−π)$.

Kidokezo

$f(x)=\sin x$ni kuendelea katika$0$. Tumia Mfano$\PageIndex{8}$ kama mwongozo.

Jibu

$0$

Ushahidi wa theorem inayofuata inatumia theorem ya kazi ya Composite pamoja na mwendelezo wa$f(x)=\sin x$ na$g(x)=\cos x$ wakati$0$ wa kuonyesha kwamba kazi za trigonometric zinaendelea juu ya nyanja zao zote.

Theorem$\PageIndex{3}$: Continuity of Trigonometric Functions

Kazi za trigonometric zinaendelea juu ya nyanja zao zote.

Ushahidi

Tunaanza kwa kuonyesha kwamba$\cos x$ ni kuendelea katika kila idadi halisi. Ili kufanya hivyo, ni lazima kuonyesha kwamba$\displaystyle \lim_{x→a}\cos x=\cos a$ kwa maadili yote ya$a$.

\ (\ displaystyle\ kuanza {align*}\ lim_ {x→ a}\ cos x &=\ lim_ {x→ a}\ cos (x-a) +a) & &\ maandishi {Andika upya} x=x-a+a.\\ [4pt]
&=\ lim_ {x→ a} (\ cos (x-a)\ cos a\ dhambi (x-a)\ dhambi a) & &\ maandishi {Tumia utambulisho kwa cosine ya jumla ya pembe mbili.}\\ [4pt]
&=\ cos (\ lim_ {x→ a} (x-a ))\ cos a-\ dhambi (\ lim_ {x→a} (x-a))\ dhambi & &\ maandishi {Tangu}\ lim_ {x→ a} (x-a) =0,\ maandishi {na}\ dhambi x\ maandishi {na}\ cos x\ maandishi {yanaendelea katika} 0.\\ [4pt]
&=\ cos (0)\ cos a|dhambi (0)\ dhambi & &\ maandishi {Tathmini}\ cos (0)\ maandishi {na}\ dhambi (0)\ maandishi {na kurahisisha.}\\ [4pt]
&= 1\ cos a -0\ sin a=\ cos a.\ mwisho {align*}\)

Ushahidi$\sin x$ unaoendelea katika kila nambari halisi ni sawa. Kwa sababu kazi zilizobaki za trigonometric zinaweza kuelezwa kwa suala la$\sin x$ na$\cos x$, mwendelezo wao unafuata kutoka kwa sheria ya kikomo cha quotient.

□

Kama unaweza kuona, theorem ya kazi ya composite ni muhimu sana katika kuonyesha uendelezaji wa kazi za trigonometric. Tunapoendelea kujifunza kwa calculus, tunatazama tena theorem hii mara nyingi.

Theorem ya Thamani ya Kati

Kazi zinazoendelea juu ya vipindi vya fomu$[a,b]$, wapi$a$ na$b$ ni namba halisi, zinaonyesha mali nyingi muhimu. Katika utafiti wetu wa calculus, tutakutana na theorems nyingi za nguvu kuhusu kazi hizo. Ya kwanza ya theorems hizi ni Theorem ya Thamani ya Kati.

Theorem ya Thamani ya Kati

Hebu$f$ uendelee juu ya muda uliofungwa, uliowekwa$[a,b]$. Kama$z$ ni idadi yoyote halisi kati$f(a)$ na$f(b)$, basi kuna idadi$c$ katika$[a,b]$ kuridhisha$f(c)=z$ katika Kielelezo$\PageIndex{7}$.

Kielelezo$\PageIndex{7}$: Kuna idadi$c ∈ [a,b]$ ambayo inatimiza$f(c)=z$.

Mfano$\PageIndex{9}$: Application of the Intermediate Value Theorem

Onyesha kwamba$f(x)=x−\cos x$ ina angalau sifuri moja.

Suluhisho

Kwa kuwa$f(x)=x−\cos x$ ni kuendelea juu ya$(−∞,+∞)$, ni kuendelea juu ya muda wowote kufungwa wa fomu$[a,b]$. Ikiwa unaweza kupata muda$[a,b]$ kama huo na$f(b)$ uwe$f(a)$ na ishara tofauti, unaweza kutumia Theorem ya Theorem ya Thamani ya Kati ili kuhitimisha lazima iwe na idadi halisi$c$ kwa$(a,b)$ kuwa inatimiza$f(c)=0$. Kumbuka kwamba

$f(0)=0−\cos(0)=−1<0$

na

$f(\frac{π}{2})=\frac{π}{2}−\cos\frac{π}{2}=\frac{π}{2}>0$.

Kutumia Theorem ya Thamani ya Kati, tunaweza kuona kwamba kuna lazima iwe na idadi halisi$c$ kwa$[0,π/2]$ kuwa inatimiza$f(c)=0$. Kwa hiyo,$f(x)=x−\cos x$ ina angalau sifuri moja.

Mfano$\PageIndex{10}$: When Can You Apply the Intermediate Value Theorem?

Kama$f(x)$ ni kuendelea tena$[0,2],f(0)>0$ na$f(2)>0$, tunaweza kutumia kati Theorem Theorem Theorem kuhitimisha kwamba$f(x)$ hana zeros katika kipindi$[0,2]$? Eleza.

Suluhisho

Hapana. Theorem ya Thamani ya Kati inatuwezesha kuhitimisha kwamba tunaweza kupata thamani kati ya$f(0)$ na$f(2)$; hairuhusu sisi kuhitimisha kwamba hatuwezi kupata maadili mengine. Ili kuona hili wazi zaidi, fikiria kazi$f(x)=(x−1)^2$. Ni satisfies$f(0)=1>0,f(2)=1>0$, na$f(1)=0$.

Mfano$\PageIndex{11}$: When Can You Apply the Intermediate Value Theorem?

Kwa$f(x)=1/x,f(−1)=−1<0$ na$f(1)=1>0$. Je, tunaweza kuhitimisha kuwa$f(x)$ ina sifuri katika kipindi$[−1,1]$?

Suluhisho

Hapana. Kazi haiendelei$[−1,1]$. Theorem ya Thamani ya Kati haitumiki hapa.

Zoezi$\PageIndex{5}$

Onyesha kwamba$f(x)=x^3−x^2−3x+1$ ina sifuri juu ya muda$[0,1]$.

Kidokezo

Kupata$f(0)$ na$f(1)$. Tumia Theorem ya Thamani ya Kati.

Jibu

$f(0)=1>0,\;f(1)=−2<0;\;f(x)$ni kuendelea juu ya$[0,1]$. Inapaswa kuwa na sifuri wakati huu.

Dhana muhimu

• Kwa kazi ya kuendelea katika hatua, ni lazima kuelezwa katika hatua hiyo, kikomo yake lazima kuwepo katika hatua, na thamani ya kazi katika hatua hiyo lazima sawa thamani ya kikomo katika hatua hiyo.
• Discontinuities inaweza kuwa classified kama removable, kuruka, au usio.
• Kazi inaendelea juu ya muda wa wazi ikiwa inaendelea kila wakati. Inaendelea juu ya muda uliofungwa ikiwa inaendelea kila wakati katika mambo yake ya ndani na inaendelea katika mwisho wake.
• Theorem ya kazi ya composite inasema: Ikiwa$f(x)$ inaendelea kwa L na$\displaystyle \lim_{x→a}g(x)=L$, basi$\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L)$.

• Theorem ya Theorem ya Thamani ya Kati inathibitisha kwamba ikiwa kazi inaendelea juu ya muda uliofungwa, basi kazi inachukua kila thamani kati ya maadili katika mwisho wake.

faharasa

mwendelezo katika hatua

kazi$f(x)$ ni kuendelea katika hatua kama na tu$a$ kama zifuatazo hali tatu ni kuridhika: (1)$f(a)$ hufafanuliwa, (2)$\displaystyle \lim_{x→a}f(x)$ ipo, na (3)$\displaystyle \lim{x→a}f(x)=f(a)$

kuendelea kutoka upande wa kushoto

Kazi inaendelea kutoka upande wa kushoto$b$ ikiwa$\displaystyle \lim_{x→b^−}f(x)=f(b)$

mwendelezo kutoka kulia

kazi ni kuendelea kutoka kulia katika$a$ kama$\displaystyle \lim_{x→a^+}f(x)=f(a)$

mwendelezo juu ya muda

kazi ambayo inaweza kufuatiliwa na penseli bila kuinua penseli; kazi inaendelea juu ya muda wa wazi ikiwa inaendelea kila wakati katika kipindi; kazi$f(x)$ inaendelea juu ya muda uliofungwa wa fomu [$a,b$] ikiwa inaendelea kila hatua katika ($a,b$), na ni kuendelea kutoka kulia$a$ na kutoka kushoto$b$

discontinuity katika hatua

Kazi imekoma kwa hatua au ina discontinuity katika hatua kama si kuendelea katika hatua

kukomesha usio

Kuacha usio na mwisho hutokea kwa hatua$a$ ikiwa$\displaystyle \lim_{x→a^−}f(x)=±∞$ au$\displaystyle \lim_{x→a^+}f(x)=±∞$

Theorem ya Thamani ya Kati

Hebu$f$ kuendelea juu ya muda imefungwa imefungwa [$a,b$] ikiwa$z$ ni idadi yoyote halisi kati ya$f(a)$ na$f(b)$, basi kuna idadi$c$ katika [$a,b$] kuridhisha$f(c)=z$

kuruka kukomesha

Kusitishwa kwa kuruka hutokea kwa hatua$a$ ikiwa$\displaystyle \lim_{x→a^−}f(x)$ na$\displaystyle \lim_{x→a^+}f(x)$ zote mbili zipo, lakini$\displaystyle \lim_{x→a^−}f(x)≠\lim_{x→a^+}f(x)$

kukomesha kutolewa

Discontinuity removable hutokea katika hatua$a$ kama$f(x)$ ni discontinuous katika$a$, lakini$\displaystyle \lim_{x→a}f(x)$ ipo