Skip to main content
Global

2.3E: Mazoezi ya Sehemu ya 2.3

  1. Last updated
  2. Save as PDF
  • Page ID
    178944

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Katika mazoezi ya 1 - 4, tumia sheria za kikomo ili kutathmini kila kikomo. Kuhalalisha kila hatua kwa kuonyesha sheria zinazofaa za kikomo.

    1)\(\displaystyle \lim_{x→0}\,(4x^2−2x+3)\)

    Jibu

    Tumia sheria nyingi na sheria tofauti:

    \(\displaystyle \lim_{x→0}\,(4x^2−2x+3)=4\lim_{x→0}x^2−2\lim_{x→0}x+\lim_{x→0}3=0 + 0 + 3=3\)

    2)\(\displaystyle \lim_{x→1}\frac{x^3+3x^2+5}{4−7x}\)

    3)\(\displaystyle \lim_{x→−2}\sqrt{x^2−6x+3}\)

    Jibu
    Tumia sheria ya mizizi:\(\displaystyle \lim_{x→−2}\sqrt{x^2−6x+3}=\sqrt{\lim_{x→−2}(x^2−6x+3)}=\sqrt{19}\)

    4)\(\displaystyle \lim_{x→−1}(9x+1)^2\)

    Katika mazoezi ya 5 - 10, tumia uingizaji wa moja kwa moja ili kutathmini kikomo cha kila kazi inayoendelea.

    5)\(\displaystyle \lim_{x→7}x^2\)

    Jibu
    \(\displaystyle \lim_{x→7}x^2\;=\;49\)

    6)\(\displaystyle \lim_{x→−2}(4x^2−1)\)

    7)\(\displaystyle \lim_{x→0}\frac{1}{1+\sin x}\)

    Jibu
    \(\displaystyle \lim_{x→0}\frac{1}{1+\sin x}\;=\;1\)

    8)\(\displaystyle \lim_{x→2}e^{2x−x^2}\)

    9)\(\displaystyle \lim_{x→1}\frac{2−7x}{x+6}\)

    Jibu
    \(\displaystyle \lim_{x→1}\frac{2−7x}{x+6}\;=\;−\frac{5}{7}\)

    10)\(\displaystyle \lim_{x→3}\ln e^{3x}\)

    Katika mazoezi 11 - 20, tumia ubadilishaji wa moja kwa moja ili kuonyesha kwamba kila kikomo kinasababisha fomu isiyo ya kawaida\(0/0\). Kisha, tathmini kikomo kwa uchambuzi.

    11)\(\displaystyle \lim_{x→4}\frac{x^2−16}{x−4}\)

    Jibu
    \(\displaystyle \text{When }x = 4, \quad\frac{x^2−16}{x−4}=\frac{16−16}{4−4}=\frac{0}{0};\)

    basi,\(\displaystyle \lim_{x→4}\frac{x^2−16}{x−4}= \lim_{x→4}\frac{(x+4)(x−4)}{x−4}=\lim_{x→4}(x+4) = 4+4 =8\)

    12)\(\displaystyle \lim_{x→2}\frac{x−2}{x^2−2x}\)

    13)\(\displaystyle \lim_{x→6}\frac{3x−18}{2x−12}\)

    Jibu
    \(\displaystyle \text{When }x = 6, \quad\frac{3x−18}{2x−12}=\frac{18−18}{12−12}=\frac{0}{0};\)

    basi,\(\displaystyle \lim_{x→6}\frac{3x−18}{2x− 12}=\lim_{x→6}\frac{3(x−6)}{2(x−6)}=\lim_{x→6}\frac{3}{2}=\frac{3}{2}\)

    14)\(\displaystyle \lim_{h→0}\frac{(1+h)^2−1}{h}\)

    15)\(\displaystyle \lim_{t→9}\frac{t−9}{\sqrt{t}−3}\)

    Jibu
    \(\displaystyle \text{When }t = 9, \quad\frac{t−9}{\sqrt{t}−3}=\frac{9−9}{3−3}=\frac{0}{0};\)

    basi,\(\displaystyle \lim_{t→9}\frac{t−9}{\sqrt{t}−3} =\lim_{t→9}\frac{t−9}{\sqrt{t}−3}\frac{\sqrt{t}+3}{\sqrt{t}+3}=\lim_{t→9}\frac{(t−9)(\sqrt{t}+3)}{t - 9}=\lim_{t→9}(\sqrt{t}+3)=\sqrt{9}+3=6\)

    16)\(\displaystyle \lim_{h→0}\frac{\dfrac{1}{a+h}−\dfrac{1}{a}}{h}\), wapi\(a\) mara kwa mara yenye thamani halisi

    17)\(\displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}\)

    Jibu
    \(\displaystyle \text{When }θ = π, \quad\frac{\sin θ}{\tan θ}=\frac{\sin π}{\tan π}=\frac{0}{0};\)

    basi,\(\displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}=\lim_{θ→ π}\frac{\sin θ}{\frac{\sin θ}{\cos θ}}=\lim_{θ→π}\cos θ=\cos π=−1\)

    18)\(\displaystyle \lim_{x→1}\frac{x^3−1}{x^2−1}\)

    19)\(\displaystyle \lim_{x→1/2}\frac{2x^2+3x−2}{2x−1}\)

    Jibu
    \(\displaystyle \text{When }x=1/2, \quad\frac{2x^2+3x−2}{2x−1}=\frac{\frac{1}{2}+\frac{3}{2}−2}{1−1}=\frac{0}{0};\)

    basi,\(\displaystyle \lim_{x→ 1/2}\frac{2x^2+3x−2}{2x−1}=\lim_{x→1/2}\frac{(2x−1)(x+2)}{2x−1}=\lim_{x→1/2}(x+2)=\frac{1}{2}+2=\frac{5}{2}\)

    20)\(\displaystyle \lim_{x→−3}\frac{\sqrt{x+4}−1}{x+3}\)

    Katika mazoezi 21 - 24, tumia uingizaji wa moja kwa moja ili kupata maelezo yasiyojulikana. Kisha, tumia njia iliyotumiwa katika Mfano 9 wa sehemu hii ili kurahisisha kazi na kuamua kikomo.

    21)\(\displaystyle \lim_{x→−2^−}\frac{2x^2+7x−4}{x^2+x−2}\)

    Jibu
    \(−∞\)

    22)\(\displaystyle \lim_{x→−2^+}\frac{2x^2+7x−4}{x^2+x−2}\)

    23)\(\displaystyle \lim_{x→1^−}\frac{2x^2+7x−4}{x^2+x−2}\)

    Jibu
    \(−∞\)

    24)\(\displaystyle \lim_{x→1^+}\frac{2x^2+7x−4}{x^2+x−2}\)

    Katika mazoezi 25 - 32, kudhani kwamba\(\displaystyle \lim_{x→6}f(x)=4,\quad \lim_{x→6}g(x)=9\), na\(\displaystyle \lim_{x→6}h(x)=6\). Tumia ukweli huu tatu na sheria za kikomo ili kutathmini kila kikomo.

    25)\(\displaystyle \lim_{x→6}2f(x)g(x)\)

    Jibu
    \(\displaystyle \lim_{x→6}2f(x)g(x)=2\left(\lim_{x→6}f(x)\right)\left(\lim_{x→6}g(x)\right)=2 (4)(9)=72\)

    26)\(\displaystyle \lim_{x→6}\frac{g(x)−1}{f(x)}\)

    27)\(\displaystyle \lim_{x→6}\left(f(x)+\frac{1}{3}g(x)\right)\)

    Jibu
    \(\displaystyle \lim_{x→6}\left(f(x)+\frac{1}{3}g(x)\right)=\lim_{x→6}f(x)+\frac{1}{3}\lim_{x→6}g(x)=4+\frac{1}{3}(9)=7\)

    28)\(\displaystyle \lim_{x→6}\frac{\big(h(x)\big)^3}{2}\)

    29)\(\displaystyle \lim_{x→6}\sqrt{g(x)−f(x)}\)

    Jibu
    \(\displaystyle \lim_{x→6}\sqrt{g(x)−f(x)}=\sqrt{\lim_{x→6}g(x)−\lim_{x→6}f(x)}=\sqrt{9-4}=\sqrt{5}\)

    30)\(\displaystyle \lim_{x→6}x⋅h(x)\)

    31)\(\displaystyle \lim_{x→6}[(x+1)⋅f(x)]\)

    Jibu
    \(\displaystyle \lim_{x→6}[(x+1)f(x)]=\left(\lim_{x→6}(x+1)\right)\left(\lim_{x→6}f(x)\right)=7(4)=28\)

    32)\(\displaystyle \lim_{x→6}(f(x)⋅g(x)−h(x))\)

    [T] Katika mazoezi 33 - 35, tumia calculator kuteka grafu ya kila kazi iliyoelezwa na kipande na kujifunza grafu ili kutathmini mipaka iliyotolewa.

    33)\(f(x)=\begin{cases}x^2, & x≤3\\ x+4, & x>3\end{cases}\)

    a.\(\displaystyle \lim_{x→3^−}f(x)\)

    b.\(\displaystyle \lim_{x→3^+}f(x)\)

    Jibu

    Grafu ya kazi ya kipande na makundi mawili. Ya kwanza ni parabola x^2, ambayo ipo kwa x<=3. Vertex ni asili, inafungua juu, na kuna mduara uliofungwa mwishoni (3,9). Sehemu ya pili ni mstari x+4, ambayo ni kazi ya mstari iliyopo kwa x 3. Kuna mduara wazi (3, 7), na mteremko ni 1." style="width: 417px; height: 422px;" width="417px" height="422px" src="https://math.libretexts.org/@api/dek...02_03_202.jpeg">

    a.\(9\); b.\( 7\)

    34)\(g(x)=\begin{cases}x^3−1, & x≤0\\1, & x>0\end{cases}\)

    a.\(\displaystyle \lim_{x→0^−}g(x)\)

    b.\(\displaystyle \lim_{x→0^+}g(x)\)

    35)\(h(x)=\begin{cases}x^2−2x+1, & x<2\\3−x, & x≥2\end{cases}\)

    a.\(\displaystyle \lim_{x→2^−}h(x)\)

    b.\(\displaystyle \lim_{x→2^+}h(x)\)

    Katika mazoezi 36 - 43, tumia grafu zifuatazo na sheria za kikomo ili kutathmini kila kikomo.

    Grafu mbili za kazi za kipande. Ya juu ni f (x), ambayo ina makundi mawili ya mstari. Ya kwanza ni mstari na mteremko hasi uliopo kwa x <-3. Inakwenda kuelekea hatua (-3,0) katika x= -3. Ya pili ina mteremko unaoongezeka na huenda kwa uhakika (-3, -2) saa x=-3. Ipo kwa x -3. Vipengele vingine muhimu ni (0, 1), (-5,2), (1,2), (-7, 4), na (-9,6). Kazi ya chini ya kipande ina sehemu ya mstari na sehemu ya pembe. Sehemu ya mstari ipo kwa x <-3 na ina mteremko wa kupungua. Inakwenda (-3, -2) katika x=-3. Sehemu ya mviringo inaonekana kuwa nusu sahihi ya parabola ya ufunguzi wa chini. Inakwenda kwenye kipeo (-3,2) kwenye x=-3. Inavuka mhimili y kidogo chini ya y=-2. Vipengele vingine muhimu ni (0, -7/3), (-5,0), (1, -5), (-7, 2), na (-9, 4)." style="width: 456px; height: 935px;" width="456px" height="935px" src="https://math.libretexts.org/@api/dek...02_03_201.jpeg">

    36)\(\displaystyle \lim_{x→−3^+}(f(x)+g(x))\)

    37)\(\displaystyle \lim_{x→−3^−}(f(x)−3g(x))\)

    Jibu
    \(\displaystyle \lim_{x→−3^−}(f(x)−3g(x))=\lim_{x→−3^−}f(x)−3\lim_{x→−3^−}g(x)=0+6=6\)

    38)\(\displaystyle \lim_{x→0}\frac{f(x)g(x)}{3}\)

    39)\(\displaystyle \lim_{x→−5}\frac{2+g(x)}{f(x)}\)

    Jibu
    \(\displaystyle \lim_{x→−5}\frac{2+g(x)}{f(x)}=\frac{2+\left(\displaystyle \lim_{x→−5}g(x)\right)}{\displaystyle \lim_{x→−5}f(x)}=\frac{2+0}{2}=1\)

    40)\(\displaystyle \lim_{x→1}(f(x))^2\)

    41)\(\displaystyle \lim_{x→1}\sqrt[3]{f(x)−g(x)}\)

    Jibu
    \(\displaystyle \lim_{x→1}\sqrt[3]{f(x)−g(x)}=\sqrt[3]{\lim_{x→1}f(x)−\lim_{x→1}g(x)}=\sqrt[3]{2+5}=\sqrt[3]{7}\)

    42)\(\displaystyle \lim_{x→−7}(x⋅g(x))\)

    43)\(\displaystyle \lim_{x→−9}[x⋅f(x)+2⋅g(x)]\)

    Jibu
    \(\displaystyle \lim_{x→−9}(xf(x)+2g(x))=\left(\lim_{x→−9}x\right)\left(\lim_{x→−9}f(x)\right)+2\lim_{x→−9}g(x)=(−9)(6)+2(4)=−46\)

    Kwa mazoezi 44 - 46, tathmini kikomo kwa kutumia theorem itapunguza. Tumia calculator kwa graph kazi\(f(x),\;g(x)\), na\(h(x)\) iwezekanavyo.

    44) [T] Kweli au Uongo? Ikiwa\(2x−1≤g(x)≤x^2−2x+3\), basi\(\displaystyle \lim_{x→2}g(x)=0\).

    45) [T]\(\displaystyle \lim_{θ→0}θ^2\cos\left(\frac{1}{θ}\right)\)

    Jibu

    Kikomo ni sifuri.

    Grafu ya kazi tatu juu ya uwanja [-1,1], rangi nyekundu, kijani, na bluu kama ifuatavyo: nyekundu: theta ^ 2, kijani: theta ^ 2 * cos (1/theta), na bluu: - (theta ^ 2). Kazi nyekundu na bluu hufungua juu na chini kwa mtiririko huo kama parabolas na vipeo katika asili. Kazi ya kijani imefungwa kati ya hizo mbili.

    46)\(\displaystyle \lim_{x→0}f(x)\), wapi\(f(x)=\begin{cases}0, & x\text{ rational}\\ x^2, & x\text{ irrrational}\end{cases}\)

    47) [T] Katika fizikia, ukubwa wa uwanja wa umeme unaozalishwa na malipo ya uhakika kwa umbali\(r\) katika utupu inasimamiwa na sheria ya Coulomb:\(E(r)=\dfrac{q}{4πε_0r^2}\), ambapo\(E\) inawakilisha ukubwa wa uwanja wa umeme,\(q\) ni malipo ya chembe,\(r\) ni umbali kati ya chembe na ambapo nguvu ya shamba ni kipimo, na\(\dfrac{1}{4πε_0}\) ni mara kwa mara Coulomb ya:\(8.988×109N⋅m^2/C^2\).

    a Tumia calculator ya graphing kwa grafu\(E(r)\) kutokana na kwamba malipo ya chembe ni\(q=10^{−10}\).

    b Tathmini\(\displaystyle \lim_{r→0^+}E(r)\). Nini maana ya kimwili ya kiasi hiki? Je, ni muhimu kimwili? Kwa nini unatathmini kutoka kwa haki?

    Jibu

    a.

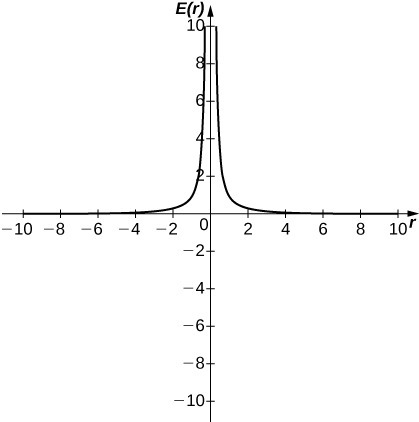
    Grafu ya kazi na curves mbili. Ya kwanza iko katika quadrant mbili na curves asymptotically kwa infinity pamoja na mhimili y na 0 pamoja na mhimili x kama x inakwenda infinity hasi. Ya pili ni katika quadrant moja na curves asymptotically kwa infinity pamoja na mhimili y na 0 pamoja mhimili x kama x inakwenda infinity.

    b. Ukubwa wa uwanja wa umeme unapokaribia chembe q inakuwa usio. Haina maana ya kimwili kutathmini umbali hasi.

    48) [T] Uzito wa kitu hutolewa na wingi wake umegawanyika na kiasi chake:\(ρ=m/V.\)

    a Tumia calculator kupanga njama kiasi kama kazi ya wiani\((V=m/ρ)\), kuchukua wewe ni kuchunguza kitu cha\(8\) kilo uzito (\(m=8\)).

    b Tathmini\(\displaystyle \lim_{x→0^+}V(\rho)\) na kuelezea maana ya kimwili.