2.3: Sheria ya Kikomo
- Page ID
- 178941
- Tambua sheria za msingi za kikomo.
- Matumizi ya sheria kikomo kutathmini kikomo ya kazi.
- Kutathmini kikomo cha kazi kwa factoring.
- Tumia sheria za kikomo ili kutathmini kikomo cha kazi ya polynomial au ya busara.
- Tathmini kikomo cha kazi kwa kuzingatia au kwa kutumia conjugates.
- Tathmini kikomo cha kazi kwa kutumia theorem itapunguza.
Katika sehemu iliyopita, tulipima mipaka kwa kuangalia grafu au kwa kujenga meza ya maadili. Katika sehemu hii, tunaanzisha sheria za kuhesabu mipaka na kujifunza jinsi ya kutumia sheria hizi. Katika Mradi wa Mwanafunzi mwishoni mwa sehemu hii, una fursa ya kutumia sheria hizi za kikomo ili kupata formula kwa eneo la mduara kwa kurekebisha njia iliyopangwa na mtaalamu wa hisabati wa Kigiriki Archimedes. Tunaanza kwa kurejesha matokeo mawili muhimu ya kikomo kutoka sehemu iliyopita. Matokeo haya mawili, pamoja na sheria za kikomo, hutumika kama msingi wa kuhesabu mipaka mingi.
Kutathmini mipaka na Sheria za Kikomo
Sheria mbili za kikomo za kwanza zilielezwa hapo awali na tunarudia hapa. Matokeo haya ya msingi, pamoja na sheria nyingine kikomo, kuruhusu sisi kutathmini mipaka ya kazi nyingi algebraic.
Kwa idadi yoyote halisi\(a\) na yoyote ya mara kwa mara\(c\),
- \(\displaystyle \lim_{x→a}x=a\)
- \(\displaystyle \lim_{x→a}c=c\)
Tathmini kila moja ya mipaka ifuatayo kwa kutumia “Basic Limit Results.”
- \(\displaystyle \lim_{x→2}x\)
- \(\displaystyle \lim_{x→2}5\)
Suluhisho
- Kikomo cha\(x\) kama\(x\) mbinu\(a\) ni\(a\):\(\displaystyle \lim_{x→2}x=2\).
- Kikomo cha mara kwa mara ni kwamba mara kwa mara:\(\displaystyle \lim_{x→2}5=5\).
Sasa tunaangalia sheria za kikomo, mali ya mtu binafsi ya mipaka. Ushahidi kwamba sheria hizi zinashikilia zimeachwa hapa.
Hebu\(f(x)\) na\(g(x)\) ufafanuliwe kwa\(x≠a\) muda wote wa wazi ulio na\(a\). Kudhani kwamba\(L\) na\(M\) ni idadi halisi kama hiyo\(\displaystyle \lim_{x→a}f(x)=L\) na\(\displaystyle \lim_{x→a}g(x)=M\). Hebu\(c\) kuwa mara kwa mara. Kisha, kila moja ya kauli zifuatazo ana:
- Sheria ya jumla kwa mipaka:
\[\displaystyle \lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M \nonumber \]
- Tofauti sheria kwa mipaka:
\[\displaystyle \lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M \nonumber \]
- Sheria nyingi za mara kwa mara kwa mipaka:
\[\displaystyle \lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber \]
- Bidhaa sheria kwa mipaka:
\[\displaystyle \lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M \nonumber \]
- Sheria ya Quotient kwa mipaka:
\[\displaystyle \lim_{x→a}\frac{f(x)}{g(x)}=\frac{\displaystyle \lim_{x→a}f(x)}{\displaystyle \lim_{x→a}g(x)}=\frac{L}{M} \nonumber \]
kwa\(M≠0\).
- Sheria ya nguvu kwa mipaka:
\[\displaystyle \lim_{x→a}\big(f(x)\big)^n=\big(\lim_{x→a}f(x)\big)^n=L^n \nonumber \]
kwa kila integer chanya\(n\).
- Sheria ya mizizi kwa mipaka:
\[\displaystyle \lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a} f(x)}=\sqrt[n]{L} \nonumber \]
kwa ajili ya wote\(L\) kama\(n\) ni isiyo ya kawaida na kwa\(L≥0\)\(n\) kuwa ni hata.
Sasa tunatumia kutumia sheria hizi za kikomo ili kutathmini kikomo.
Matumizi ya sheria kikomo kutathmini\[\lim_{x→−3}(4x+2). \nonumber \]
Suluhisho
Hebu kutumia sheria kikomo hatua moja kwa wakati kuwa na uhakika sisi kuelewa jinsi kazi. Tunahitaji kukumbuka mahitaji ambayo, katika kila matumizi ya sheria ya kikomo, mipaka mpya inapaswa kuwepo kwa sheria ya kikomo itumike.
\[\begin{align*} \lim_{x→−3}(4x+2) &= \lim_{x→−3} 4x + \lim_{x→−3} 2 & & \text{Apply the sum law.}\\[4pt] &= 4⋅\lim_{x→−3} x + \lim_{x→−3} 2 & & \text{Apply the constant multiple law.}\\[4pt] &= 4⋅(−3)+2=−10. & & \text{Apply the basic limit results and simplify.} \end{align*}\]
Matumizi ya sheria kikomo kutathmini\[\lim_{x→2}\frac{2x^2−3x+1}{x^3+4}. \nonumber \]
Suluhisho
Ili kupata kikomo hiki, tunahitaji kutumia sheria za kikomo mara kadhaa. Tena, tunahitaji kukumbuka kwamba tunapoandika upya kikomo kwa suala la mipaka mingine, kila kikomo kipya kinapaswa kuwepo kwa sheria ya kikomo itumike.
\ [kuanza {align*}\ lim_ {x→ 2}\ frac {2x^2,13x+1} {x ^ 3+4} &=\ frac {\ displaystyle\ lim_ {x→ 2} (2x^2,13x+1)} {\ displaystyle\ lim_ {x→ 2} (x ^ 3+4)} & &\ maandishi {sheria, hakikisha kwamba} (2) ^3+40.\\ [4pt]
&=\\ frac {\ displaystyle 2\ lim_ {x→ 2} x ^ 2,13\ lim_ {x→ 2} x+\ lim_ {x→ 2} {x→ 2} 1} {\ displaystyle\ lim_ {x→ 2} x ^ 3+\ lim_ {x→ 2} 4} &\ maandishi {Tumia sheria ya jumla na sheria nyingi za mara kwa mara.}\\ [4pt]
&=\ frac {\ displaystyle 2合\ kushoto (\ lim_ {x→ 2} x\ haki) ^2—3\ lim_ {x→ 2} 1} {\ displaystyle\ kushoto (\ lim_ {x→ 2} x\ kulia) ^3+\ lim_ {x→ 2} 4} & &\ maandishi {Tumia sheria ya nguvu.}\\ [4pt]
&=\ frac {2 (4) -3 (2) +1} {(2) ^3+4} =\ frac {1} {4}. & &\ maandishi {Weka sheria za kikomo za msingi na kurahisisha.} \ mwisho {align*}\]
Tumia sheria za kikomo kutathmini\(\displaystyle \lim_{x→6}(2x−1)\sqrt{x+4}\). Katika kila hatua, onyesha sheria ya kikomo iliyotumiwa.
- Kidokezo
-
Anza kwa kutumia sheria ya bidhaa.
- Jibu
-
\(11\sqrt{10}\)
Mbinu za Tathmini ya Ziada
Kama tulivyoona, tunaweza kutathmini kwa urahisi mipaka ya polynomials na mipaka ya baadhi (lakini si wote) kazi ya busara na badala ya moja kwa moja. Hata hivyo, kama tulivyoona katika sehemu ya utangulizi juu ya mipaka, ni hakika inawezekana\(\displaystyle \lim_{x→a}f(x)\) kwa kuwepo wakati\(f(a)\) ni undefined. Uchunguzi wafuatayo unatuwezesha kutathmini mipaka mingi ya aina hii:
Kama kwa muda wote\(x≠a,\;f(x)=g(x)\) juu ya baadhi ya wazi zenye\(a\), basi
\[\displaystyle\lim_{x→a}f(x)=\lim_{x→a}g(x). \nonumber \]
Ili kuelewa wazo hili vizuri, fikiria kikomo\(\displaystyle \lim_{x→1}\dfrac{x^2−1}{x−1}\).
Kazi
\[f(x)=\dfrac{x^2−1}{x−1}=\dfrac{(x−1)(x+1)}{x−1}\nonumber \]
na kazi\(g(x)=x+1\) ni sawa kwa maadili yote ya\(x≠1\). Grafu ya kazi hizi mbili zinaonyeshwa kwenye Kielelezo\(\PageIndex{1}\).
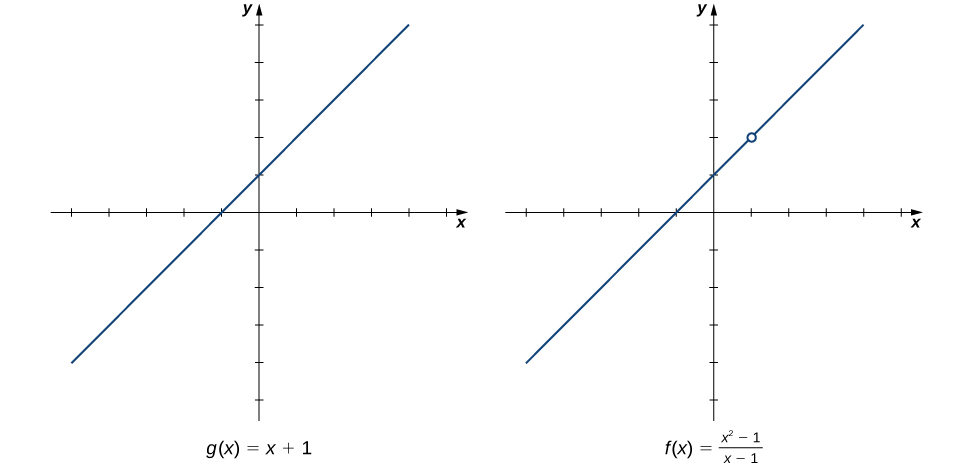
Tunaona kwamba
\[\lim_{x→1}\dfrac{x^2−1}{x−1}=\lim_{x→1}\dfrac{(x−1)(x+1)}{x−1}=\lim_{x→1}\,(x+1)=2.\nonumber \]
Kikomo kina fomu\(\displaystyle \lim_{x→a}f(x)/g(x)\), wapi\(\displaystyle\lim_{x→a}f(x)=0\) na\(\displaystyle\lim_{x→a}g(x)=0\). (Katika kesi hii, tunasema kwamba\(f(x)/g(x)\) ina fomu indeterminate\(0/0\).) Mkakati unaofuata wa kutatua matatizo hutoa muhtasari wa jumla wa kutathmini mipaka ya aina hii.
- Kwanza, tunahitaji kuhakikisha kuwa kazi yetu ina fomu inayofaa na haiwezi kutathminiwa mara moja kwa kutumia sheria za kikomo.
- Sisi kisha haja ya kupata kazi ambayo ni sawa na\(h(x)=f(x)/g(x)\) kwa wote\(x≠a\) juu ya baadhi ya muda zenye Ili kufanya hivyo, tunaweza haja ya kujaribu moja au zaidi ya hatua zifuatazo:
- Kama\(f(x)\) na\(g(x)\) ni polynomials, tunapaswa sababu kila kazi na kufuta mambo yoyote ya kawaida.
- Ikiwa nambari au denominator ina tofauti inayohusisha mizizi ya mraba, tunapaswa kujaribu kuzidisha nambari na denominator kwa conjugate ya kujieleza inayohusisha mizizi ya mraba.
- Ikiwa\(f(x)/g(x)\) ni sehemu ngumu, tunaanza kwa kurahisisha.
- Mwisho, tunatumia sheria za kikomo.
Mifano inayofuata inaonyesha matumizi ya Mkakati huu wa kutatua matatizo. Mfano\(\PageIndex{4}\) unaeleza sababu na-kufuta mbinu; Mfano\(\PageIndex{5}\) inaonyesha kuzidisha kwa conjugate. Katika Mfano\(\PageIndex{6}\), tunaangalia kurahisisha sehemu ngumu.
Tathmini\(\displaystyle\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}\).
Suluhisho
Hatua ya 1. kazi\(f(x)=\dfrac{x^2−3x}{2x^2−5x−3}\) ni undefined kwa\(x=3\). Kwa kweli, kama sisi badala 3 katika kazi sisi kupata\(0/0\), ambayo ni undefined. Kuzingatia na kufuta ni mkakati mzuri:
\[\lim_{x→3}\dfrac{x^2−3x}{2x^2−5x−3}=\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}\nonumber \]
Hatua ya 2. Kwa ajili ya wote\(x≠3,\dfrac{x^2−3x}{2x^2−5x−3}=\dfrac{x}{2x+1}\). Kwa hiyo,
\[\lim_{x→3}\dfrac{x(x−3)}{(x−3)(2x+1)}=\lim_{x→3}\dfrac{x}{2x+1}.\nonumber \]
Hatua ya 3. Tathmini kutumia sheria za kikomo:
\[\lim_{x→3}\dfrac{x}{2x+1}=\dfrac{3}{7}.\nonumber \]
Tathmini\(\displaystyle \lim_{x→−3}\dfrac{x^2+4x+3}{x^2−9}\).
- Kidokezo
-
Fuata hatua katika Mkakati wa Kutatua Matatizo
- Jibu
-
\(\dfrac{1}{3}\)
Tathmini\( \displaystyle \lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}\).
Suluhisho
Hatua ya 1. \( \displaystyle \dfrac{\sqrt{x+2}−1}{x+1}\)ina fomu\(0/0\) katika -1. Hebu tuanze kwa kuzidisha na\(\sqrt{x+2}+1\), conjugate ya\(\sqrt{x+2}−1\), juu ya nambari na denominator:
\[\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}=\lim_{x→−1}\dfrac{\sqrt{x+2}−1}{x+1}⋅\dfrac{\sqrt{x+2}+1}{\sqrt{x+2}+1}.\nonumber \]
Hatua ya 2. Sisi kisha kuzidisha nambari. Hatuzidishi denominator kwa sababu tunatarajia kwamba\((x+1)\) katika denominator inafuta mwishoni:
\[=\lim_{x→−1}\dfrac{x+1}{(x+1)(\sqrt{x+2}+1)}.\nonumber \]
Hatua ya 3. Kisha sisi kufuta:
\[= \lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}.\nonumber \]
Hatua ya 4. Mwisho, tunatumia sheria za kikomo:
\[\lim_{x→−1}\dfrac{1}{\sqrt{x+2}+1}=\dfrac{1}{2}.\nonumber \]
Tathmini\( \displaystyle \lim_{x→5}\dfrac{\sqrt{x−1}−2}{x−5}\).
- Kidokezo
-
Fuata hatua katika Mkakati wa Kutatua Matatizo
- Jibu
-
\(\dfrac{1}{4}\)
Tathmini\( \displaystyle \lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}\).
Suluhisho
Hatua ya 1. \(\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}\)ina fomu\(0/0\) katika 1. Sisi kurahisisha sehemu ya algebraic kwa kuzidisha na\(2(x+1)/2(x+1)\):
\[\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}=\lim_{x→1}\dfrac{\dfrac{1}{x+1}−\dfrac{1}{2}}{x−1}⋅\dfrac{2(x+1)}{2(x+1)}.\nonumber \]
Hatua ya 2. Kisha, tunazidisha kupitia nambari za nambari. Je, si kuzidisha denominators kwa sababu tunataka kuwa na uwezo wa kufuta sababu\((x−1)\):
\[=\lim_{x→1}\dfrac{2−(x+1)}{2(x−1)(x+1)}.\nonumber \]
Hatua ya 3. Kisha, sisi kurahisisha nambari:
\[=\lim_{x→1}\dfrac{−x+1}{2(x−1)(x+1)}.\nonumber \]
Hatua ya 4. Sasa tunazingatia -1 kutoka kwa nambari:
\[=\lim_{x→1}\dfrac{−(x−1)}{2(x−1)(x+1)}.\nonumber \]
Hatua ya 5. Kisha, sisi kufuta mambo ya kawaida ya\((x−1)\):
\[=\lim_{x→1}\dfrac{−1}{2(x+1)}.\nonumber \]
Hatua ya 6. Mwisho, tunatathmini kutumia sheria za kikomo:
\[\lim_{x→1}\dfrac{−1}{2(x+1)}=−\dfrac{1}{4}.\nonumber \]
Tathmini\( \displaystyle \lim_{x→−3}\dfrac{\dfrac{1}{x+2}+1}{x+3}\).
- Kidokezo
-
Fuata hatua katika Mkakati wa Kutatua Matatizo
- Jibu
-
-1
Mfano\(\PageIndex{7}\) hauingii vizuri katika mifumo yoyote iliyoanzishwa katika mifano ya awali. Hata hivyo, kwa ubunifu kidogo, bado tunaweza kutumia mbinu hizi sawa.
Tathmini\( \displaystyle \lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)\).
Suluhisho:
Wote\(1/x\) na\(5/x(x−5)\) kushindwa kuwa na kikomo katika sifuri. Kwa kuwa hakuna kazi mbili zina kikomo cha sifuri, hatuwezi kutumia sheria ya jumla kwa mipaka; lazima tutumie mkakati tofauti. Katika kesi hii, tunapata kikomo kwa kufanya kuongeza na kisha kutumia moja ya mikakati yetu ya awali. Kuzingatia kwamba
\[\dfrac{1}{x}+\dfrac{5}{x(x−5)}=\dfrac{x−5+5}{x(x−5)}=\dfrac{x}{x(x−5)}.\nonumber \]
Hivyo,
\[\lim_{x→0}\left(\dfrac{1}{x}+\dfrac{5}{x(x−5)}\right)=\lim_{x→0}\dfrac{x}{x(x−5)}=\lim_{x→0}\dfrac{1}{x−5}=−\dfrac{1}{5}.\nonumber \]
Tathmini\( \displaystyle \lim_{x→3}\left(\dfrac{1}{x−3}−\dfrac{4}{x^2−2x−3}\right)\).
- Kidokezo
-
Tumia mbinu sawa na Mfano\(\PageIndex{7}\). Usisahau sababu\(x^2−2x−3\) kabla ya kupata denominator ya kawaida.
- Jibu
-
\(\dfrac{1}{4}\)
Hebu sasa tupate upya mipaka ya upande mmoja. Marekebisho rahisi katika sheria za kikomo hutuwezesha kuitumia kwa mipaka ya upande mmoja. Kwa mfano, kuomba sheria za kikomo kwa kikomo cha fomu\(\displaystyle \lim_{x→a^−}h(x)\), tunahitaji kazi\(h(x)\) kufafanuliwa juu ya muda wa wazi wa fomu\((b,a)\); kwa kikomo cha fomu\(\displaystyle \lim_{x→a^+}h(x)\), tunahitaji kazi\(h(x)\) kufafanuliwa juu ya muda wa wazi wa fomu\((a,c)\). Mfano\(\PageIndex{8A}\) unaeleza hatua hii.
Tathmini kila moja ya mipaka ifuatayo, ikiwa inawezekana.
- \(\displaystyle \lim_{x→3^−}\sqrt{x−3}\)
- \( \displaystyle \lim_{x→3^+}\sqrt{x−3}\)
Suluhisho
Kielelezo\(\PageIndex{2}\) unaeleza kazi\(f(x)=\sqrt{x−3}\) na misaada katika ufahamu wetu wa mipaka hii.
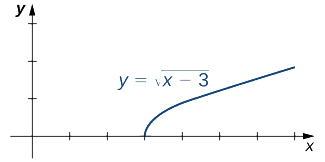
a. kazi\(f(x)=\sqrt{x−3}\) hufafanuliwa juu ya muda\([3,+∞)\). Kwa kuwa kazi hii haijafafanuliwa upande wa kushoto wa 3, hatuwezi kutumia sheria za kikomo kukokotoa\(\displaystyle\lim_{x→3^−}\sqrt{x−3}\). Kwa kweli, tangu\(f(x)=\sqrt{x−3}\) haijulikani upande wa kushoto wa 3,\(\displaystyle\lim_{x→3^−}\sqrt{x−3}\) haipo.
b. tangu\(f(x)=\sqrt{x−3}\) hufafanuliwa na haki ya 3, sheria kikomo kufanya yanahusu\(\displaystyle\lim_{x→3^+}\sqrt{x−3}\). Kwa kutumia sheria hizi kikomo sisi kupata\(\displaystyle\lim_{x→3^+}\sqrt{x−3}=0\).
Katika Mfano\(\PageIndex{8B}\) tunaangalia mipaka ya upande mmoja wa kazi iliyofafanuliwa na kipande na kutumia mipaka hii kuteka hitimisho kuhusu kikomo cha upande mmoja wa kazi hiyo.
Kwa\(f(x)=\begin{cases}4x−3, & \mathrm{if} \; x<2 \\ (x−3)^2, & \mathrm{if} \; x≥2\end{cases}\), tathmini kila moja ya mipaka ifuatayo:
- \(\displaystyle \lim_{x→2^−}f(x)\)
- \(\displaystyle \lim_{x→2^+}f(x)\)
- \(\displaystyle \lim_{x→2}f(x)\)
Suluhisho
Kielelezo\(\PageIndex{3}\) unaeleza kazi\(f(x)\) na misaada katika ufahamu wetu wa mipaka hii.
a. tangu\(f(x)=4x−3\) kwa wote\(x\) katika\((−∞,2)\), kuchukua nafasi\(f(x)\) katika kikomo\(4x−3\) na kutumia sheria kikomo:
\[\lim_{x→2^−}f(x)=\lim_{x→2^−}(4x−3)=5\nonumber \]
b. tangu\(f(x)=(x−3)^2\) kwa wote\(x\) katika\((2,+∞)\), kuchukua nafasi\(f(x)\) katika kikomo\((x−3)^2\) na kutumia sheria kikomo:
\[\lim_{x→2^+}f(x)=\lim_{x→2^−}(x−3)^2=1. \nonumber \]
c. tangu\(\displaystyle \lim_{x→2^−}f(x)=5\) na\(\displaystyle \lim_{x→2^+}f(x)=1\), sisi kuhitimisha kwamba\(\displaystyle \lim_{x→2}f(x)\) haipo.
Grafu\(f(x)=\begin{cases}−x−2, & \mathrm{if} \; x<−1\\ 2, & \mathrm{if} \; x=−1 \\ x^3, & \mathrm{if} \; x>−1\end{cases}\) na tathmini\(\displaystyle \lim_{x→−1^−}f(x)\).
- Kidokezo
-
Tumia njia katika Mfano\(\PageIndex{8B}\) ili kutathmini kikomo.
- Jibu
-
-1, ambayo ilivuka mhimili x na y mhimili katika asili." src="https://math.libretexts.org/@api/dek...02_03_004.jpeg">
\[\lim_{x→−1^−}f(x)=−1\nonumber \]
Sasa tunageuka mawazo yetu kutathmini kikomo cha fomu\(\displaystyle \lim_{x→a}\dfrac{f(x)}{g(x)}\), wapi\(\displaystyle \lim_{x→a}f(x)=K\), wapi\(K≠0\) na\(\displaystyle \lim_{x→a}g(x)=0\). Hiyo ni,\(f(x)/g(x)\) ina fomu\(K/0,K≠0\) katika\(a\).
Tathmini\(\displaystyle \lim_{x→2^−}\dfrac{x−3}{x^2−2x}\).
Suluhisho
Hatua ya 1. Baada ya kuingia\(x=2\), tunaona kwamba kikomo hiki kina fomu\(−1/0\). Hiyo ni, kama\(x\) mbinu\(2\) kutoka upande wa kushoto, namba inakaribia\(−1\); na denominator inakaribia\(0\). Kwa hiyo, ukubwa wa\(\dfrac{x−3}{x(x−2)} \) inakuwa usio. Ili kupata wazo bora la kikomo ni nini, tunahitaji kuzingatia denominator:
\[\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=\lim_{x→2^−}\dfrac{x−3}{x(x−2)} \nonumber \]
Hatua ya 2. Kwa kuwa\(x−2\) ni sehemu tu ya denominator yaani sifuri wakati 2 ni kubadilishwa, sisi kisha\(1/(x−2)\) tofauti na mapumziko ya kazi:
\[=\lim_{x→2^−}\dfrac{x−3}{x}⋅\dfrac{1}{x−2} \nonumber \]
Hatua ya 3. Kutumia Sheria za Kikomo, tunaweza kuandika:
\[=\left(\lim_{x→2^−}\dfrac{x−3}{x}\right)\cdot\left(\lim_{x→2^−}\dfrac{1}{x−2}\right). \nonumber \]
Hatua ya 4. \(\displaystyle \lim_{x→2^−}\dfrac{x−3}{x}=−\dfrac{1}{2}\)na\(\displaystyle \lim_{x→2^−}\dfrac{1}{x−2}=−∞\). Kwa hiyo, bidhaa ya\((x−3)/x\) na\(1/(x−2)\) ina kikomo cha\(+∞\):
\[\lim_{x→2^−}\dfrac{x−3}{x^2−2x}=+∞. \nonumber \]
Tathmini\(\displaystyle \lim_{x→1}\dfrac{x+2}{(x−1)^2}\).
- Suluhisho
-
Tumia mbinu kutoka kwa Mfano\(\PageIndex{9}\).
- Jibu
-
\(+∞\)
Theorem itapunguza
Mbinu ambazo tumeziendeleza hadi sasa zinafanya kazi vizuri sana kwa kazi za algebraic, lakini bado hatuwezi kutathmini mipaka ya kazi za msingi za trigonometric. Theorem inayofuata, inayoitwa theorem itapunguza, inathibitisha muhimu sana kwa kuanzisha mipaka ya msingi ya trigonometric. Theorem hii inaruhusu sisi kuhesabu mipaka kwa “kufinya” kazi, na kikomo katika hatua\(a\) ambayo haijulikani, kati ya kazi mbili kuwa kawaida inayojulikana kikomo katika\(a\). Kielelezo\(\PageIndex{4}\) unaeleza wazo hili.
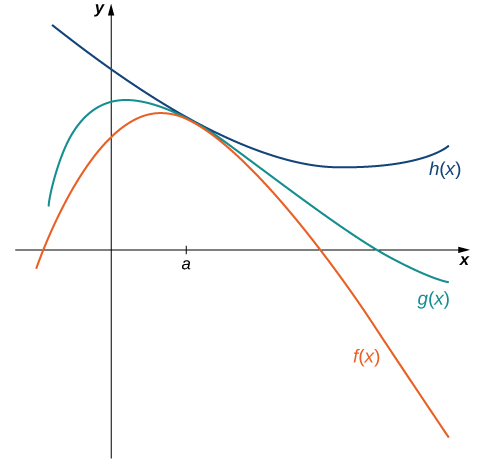
Hebu\(f(x),g(x)\), na\(h(x)\) ufafanuliwe kwa\(x≠a\) muda wote wa wazi ulio na\(a\). Kama
\[f(x)≤g(x)≤h(x) \nonumber \]
kwa wote\(x≠a\) katika kipindi cha wazi kilicho\(a\) na
\[\lim_{x→a}f(x)=L=\lim_{x→a}h(x) \nonumber \]
\(L\)wapi idadi halisi, basi\(\displaystyle \lim_{x→a}g(x)=L.\)
Tumia theorem itapunguza kutathmini\(\displaystyle \lim_{x→0} x \cos x\).
Suluhisho
\(−1≤\cos x≤1\)Kwa sababu kwa wote\(x\), tuna\(−x≤x \cos x≤x\) kwa\(x≥0\) na\(−x≥x \cos x ≥ x\) kwa\(x≤0\) (ikiwa\(x\) ni hasi mwelekeo wa kutofautiana hubadilika wakati tunapozidisha). Tangu\(\displaystyle \lim_{x→0}(−x)=0=\lim_{x→0}x\), kutoka kwa theorem itapunguza, tunapata\(\displaystyle \lim_{x→0}x \cos x=0\). grafu ya\(f(x)=−x,\;g(x)=x\cos x\), na\(h(x)=x\) ni inavyoonekana katika Kielelezo\(\PageIndex{5}\).
Tumia theorem itapunguza kutathmini\(\displaystyle \lim_{x→0}x^2 \sin\dfrac{1}{x}\).
- Kidokezo
-
Tumia ukweli kwamba\(−x^2≤x^2\sin (1/x) ≤ x^2\) kukusaidia kupata kazi mbili ambazo\(x^2\sin (1/x)\) zimechapishwa kati yao.
- Jibu
-
0
Sasa tunatumia theorem itapunguza kukabiliana na mipaka kadhaa muhimu sana. Ingawa mjadala huu ni wa muda mrefu, mipaka hii inathibitisha thamani sana kwa ajili ya maendeleo ya nyenzo katika sehemu inayofuata na sura inayofuata. Ya kwanza ya mipaka hii ni\(\displaystyle \lim_{θ→0}\sin θ\). Fikiria mduara wa kitengo umeonyeshwa kwenye Kielelezo\(\PageIndex{6}\). Katika takwimu, tunaona kwamba\(\sin θ\) ni\(y\) -kuratibu kwenye mduara wa kitengo na inafanana na sehemu ya mstari iliyoonyeshwa kwa bluu. Kipimo cha radian cha angle\(θ\) ni urefu wa arc kinachozunguka kwenye mduara wa kitengo. Kwa hiyo, tunaona kwamba kwa\(0<θ<\dfrac{π}{2},\) tuna\(0<\sin θ<θ.\)
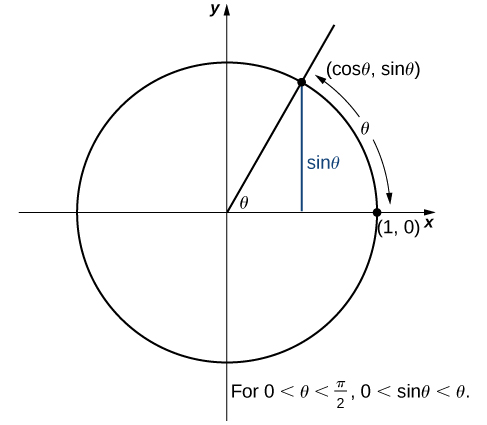
Kwa sababu\(\displaystyle \lim_{θ→0^+}0=0\) na\(\displaystyle \lim_{x→0^+}θ=0\), kwa kutumia theorem itapunguza sisi kuhitimisha kwamba
\[\lim_{θ→0^+}\sin θ=0.\nonumber \]
Ili kuona kwamba\(\displaystyle \lim_{θ→0^−}\sin θ=0\) pia, angalia hilo kwa\(−\dfrac{π}{2}<θ<0,0<−θ<\dfrac{π}{2}\) na hivyo,\(0<\sin(−θ)<−θ\). Kwa hiyo,\(0<−\sin θ<−θ\). Inafuata kwamba\(0>\sin θ>θ\). Matumizi ya theorem itapunguza hutoa kikomo kilichohitajika. Hivyo, tangu\(\displaystyle \lim_{θ→0^+}\sin θ=0\) na\(\displaystyle \lim_{θ→0^−}\sin θ=0\),
\[\lim_{θ→0}\sin θ=0\nonumber \]
Next, kwa kutumia utambulisho\(\cos θ=\sqrt{1−\sin^2θ}\) kwa\(−\dfrac{π}{2}<θ<\dfrac{π}{2}\), tunaona kwamba
\[\lim_{θ→0}\cos θ=\lim_{θ→0}\sqrt{1−\sin^2θ}=1.\nonumber \]
Sasa tunaangalia kikomo ambacho kina jukumu muhimu katika sura za baadaye-yaani,\(\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}\). Ili kutathmini kikomo hiki, tunatumia mduara wa kitengo kwenye Kielelezo\(\PageIndex{7}\). Kumbuka kwamba takwimu hii anaongeza pembetatu moja ya ziada kwa Kielelezo\(\PageIndex{6}\). Tunaona kwamba urefu wa upande kinyume cha pembe\(θ\) katika pembetatu hii mpya ni\(\tan θ\). Hivyo, tunaona kwamba kwa\(0<θ<\dfrac{π}{2}\), tuna\(\sin θ<θ<\tanθ\).
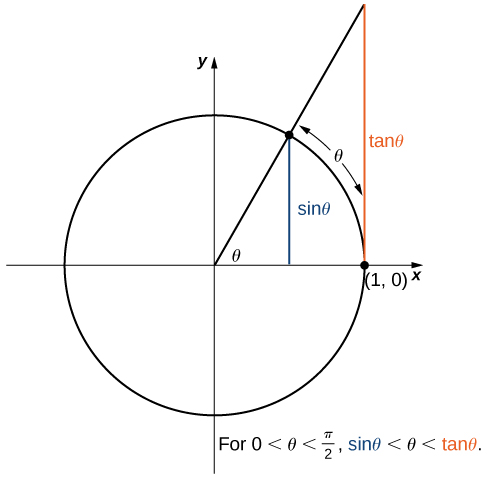
Kwa kugawa na\(\sin θ\) katika maeneo yote ya kukosekana kwa usawa, sisi kupata
\[1<\dfrac{θ}{\sin θ}<\dfrac{1}{\cos θ}.\nonumber \]
Equivalently, tuna
\[1>\dfrac{\sin θ}{θ}>\cos θ.\nonumber \]
Tangu\(\displaystyle \lim_{θ→0^+}1=1=\lim_{θ→0^+}\cos θ\), tunahitimisha kwamba\(\displaystyle \lim_{θ→0^+}\dfrac{\sin θ}{θ}=1\), kwa theorem itapunguza. Kwa kutumia udanganyifu sawa na ule uliotumiwa katika kuonyesha kwamba\(\displaystyle \lim_{θ→0^−}\sin θ=0\), tunaweza kuonyesha hilo\(\displaystyle \lim_{θ→0^−}\dfrac{\sin θ}{θ}=1\). Hivyo,
\[\lim_{θ→0}\dfrac{\sin θ}{θ}=1. \nonumber \]
Katika Mfano\(\PageIndex{11}\), tunatumia kikomo hiki kuanzisha\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0\). Kikomo hiki pia kinathibitisha kuwa muhimu katika sura za baadaye.
Tathmini\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{θ}\).
Suluhisho
Katika hatua ya kwanza, tunazidisha na conjugate ili tuweze kutumia utambulisho wa trigonometric kubadili cosine katika nambari kwa sine:
\ [kuanza {align*}\ lim_ {ρ→ 0}\ dfrac {1-\ cos η} {η} &=\ displaystyle\ lim_ {ρ→ 0}\ dfrac {1 ÷\ cos ρ} {坪}\ dfrac {1+\ cos ρ}\\ [4pt]
&=\ lim_ {ν → 0} dfrac {1-\ cos ^2η} {η (1+\ cos η)}\\ [4pt]
&=\ lim_ {ρ→ 0}\ dfrac {\ dhambi ^2} {η (1+\ cos η)}\\ [4pt]
&=\ lim_ {→ 0}\ dfrac {\ dhambi η } {ρ}}\ dfrac {\ dhambi η} {1+\ cos η}\\ [4pt]
&=\ kushoto (\ lim_ {ρ→ 0}\ dfrac {\ dhambi η} {η}\ haki)\ cdot\ kushoto (\ lim_ {ν → 0}\ dfrac {\ dhambi η} {1+\ cos η}\ haki)\\ [4pt]
&= 1\ dfrac {0} {2} =0. \ mwisho {align*}\]
Kwa hiyo,
\[\lim_{θ→0}\dfrac{1−\cos θ}{θ}=0. \nonumber \]
Tathmini\(\displaystyle \lim_{θ→0}\dfrac{1−\cos θ}{\sin θ}\).
- Kidokezo
-
Kuzidisha nambari na denominator na\(1+\cos θ\).
- Jibu
-
0
Baadhi ya formula kijiometri sisi kuchukua kwa nafasi leo walikuwa kwanza inayotokana na mbinu kwamba wanatarajia baadhi ya mbinu za calculus. Mtaalamu wa hisabati wa Kigiriki Archimedes (ca. 287—212; BCE) alikuwa mwenye ubunifu hasa, akitumia polygoni zilizoandikwa ndani ya miduara ili kukadiria eneo la mduara kadiri idadi ya pande za poligoni iliongezeka. Hajawahi kuja na wazo la kikomo, lakini tunaweza kutumia wazo hili kuona nini ujenzi wake wa kijiometri ungeweza kutabiri kuhusu kikomo.
Tunaweza kukadiria eneo la mduara kwa kompyuta eneo la polygon iliyoandikwa mara kwa mara. Fikiria polygon ya kawaida kama inaundwa na\(n\) pembetatu. Kwa kuchukua kikomo kama angle vertex ya pembetatu hizi inakwenda sifuri, unaweza kupata eneo la mduara. Ili kuona hili, fanya hatua zifuatazo:
1.Express urefu\(h\) na msingi\(b\) wa pembetatu ya isosceles\(\PageIndex{8}\) katika Kielelezo kwa suala la\(θ\) na\(r\).
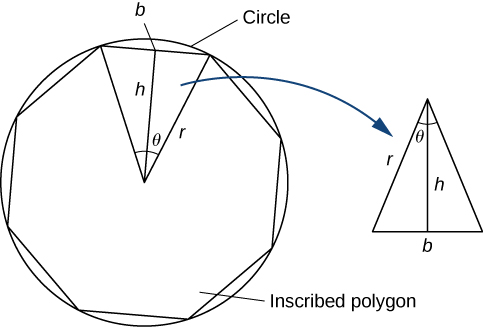
2. Kutumia maneno uliyopata katika hatua ya 1, onyesha eneo la pembetatu ya isosceles kwa suala la\(θ\) na\(r\).
(Mbadala\(\frac{1}{2}\sin θ\) kwa ajili ya\(\sin\left(\frac{θ}{2}\right)\cos\left(\frac{θ}{2}\right)\) katika usemi wako.)
3. Ikiwa poligoni ya kawaida ya\(n\) upande mmoja imeandikwa kwenye mduara wa radius\(r\), pata uhusiano kati\(θ\) na\(n\). Tatua hili kwa\(n\). Kumbuka kuna\(2π\) radians katika mduara. (Tumia radians, si digrii.)
4. Pata maelezo kwa eneo la polygon ya\(n\) upande mmoja kwa suala la\(r\) na\(θ\).
5. Ili kupata formula kwa eneo la mduara, pata kikomo cha kujieleza katika hatua ya 4 kama\(θ\) inakwenda sifuri. (Kidokezo:\(\displaystyle \lim_{θ→0}\dfrac{\sin θ}{θ}=1)\).
Mbinu ya kukadiria maeneo ya mikoa kwa kutumia polygoni inarekebishwa katika Utangulizi wa Ushirikiano.
Dhana muhimu
- Sheria za kikomo zinatuwezesha kutathmini mipaka ya kazi bila ya kwenda kupitia taratibu za hatua kwa hatua kila wakati.
- Kwa polynomials na kazi za busara,\[\lim_{x→a}f(x)=f(a). \nonumber \]
- Unaweza kutathmini kikomo cha kazi kwa kuzingatia na kufuta, kwa kuzidisha kwa conjugate, au kwa kurahisisha sehemu tata.
- Theorem itapunguza inakuwezesha kupata kikomo cha kazi ikiwa kazi daima ni kubwa kuliko kazi moja na chini ya kazi nyingine na mipaka inayojulikana.
Mlinganyo muhimu
- Matokeo ya Msingi ya Kikomo
\[\lim_{x→a}x=a \quad \quad \lim_{x→a}c=c \nonumber \]
- Mipaka muhimu
\[ \lim_{θ→0}\sin θ=0 \nonumber \]
\[ \lim_{θ→0}\cos θ=1 \nonumber \]
\[ \lim_{θ→0}\dfrac{\sin θ}{θ}=1 \nonumber \]
\[ \lim_{θ→0}\dfrac{1−\cos θ}{θ}=0 \nonumber \]
faharasa
- sheria nyingi za mara kwa mara kwa mipaka
- sheria ya kikomo\[\lim_{x→a}cf(x)=c⋅\lim_{x→a}f(x)=cL \nonumber \]
- sheria tofauti kwa mipaka
- sheria ya kikomo\[\lim_{x→a}(f(x)−g(x))=\lim_{x→a}f(x)−\lim_{x→a}g(x)=L−M\nonumber \]
- sheria za kikomo
- mali ya mtu binafsi ya mipaka; kwa kila sheria za mtu binafsi, basi\(f(x)\) na\(g(x)\) ufafanuliwe kwa\(x≠a\) muda wote wa wazi ulio na; kudhani kwamba L na M ni namba halisi ili\(\lim_{x→a}f(x)=L\) na\(\lim_{x→a}g(x)=M\); basi c iwe mara kwa mara
- sheria ya nguvu kwa mipaka
- sheria kikomo\[\lim_{x→a}(f(x))^n=(\lim_{x→a}f(x))^n=L^n\nonumber \] kwa kila n chanya integer
- sheria ya bidhaa kwa mipaka
- sheria ya kikomo\[\lim_{x→a}(f(x)⋅g(x))=\lim_{x→a}f(x)⋅\lim_{x→a}g(x)=L⋅M\nonumber \]
- sheria ya quotient kwa mipaka
- sheria ya kikomo\(\lim_{x→a}\dfrac{f(x)}{g(x)}=\dfrac{\lim_{x→a}f(x)}{\lim_{x→a}g(x)}=\dfrac{L}{M}\) kwa M0
- sheria ya mizizi kwa mipaka
- sheria kikomo\(\lim_{x→a}\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x→a}f(x)}=\sqrt[n]{L}\) kwa L wote kama n ni isiyo ya kawaida na kwa ajili ya\(L≥0\) kama n ni hata
- itapunguza theorem
- inasema kwamba ikiwa\(f(x)≤g(x)≤h(x)\) kwa\(x≠a\) muda wote wa wazi ulio na\(\lim_{x→a}f(x)=L=\lim_ {x→a}h(x)\) wapi L ni namba halisi, basi\(\lim_{x→a}g(x)=L\)
- jumla ya sheria kwa mipaka
- Sheria ya kikomo\(\lim_{x→a}(f(x)+g(x))=\lim_{x→a}f(x)+\lim_{x→a}g(x)=L+M\)



Mipaka ya Kazi za Polynomial na za busara
Kwa sasa umeona kuwa, katika kila moja ya mifano ya awali, imekuwa kesi hiyo\(\displaystyle \lim_{x→a}f(x)=f(a)\). Hii sio kweli kila wakati, lakini inashikilia kwa polynomials wote kwa uchaguzi wowote wa\(a\) na kwa kazi zote za busara\(a\) kwa maadili yote ambayo kazi ya busara inaelezwa.
Mipaka ya Kazi za Polynomial na za busara
Hebu\(p(x)\) na\(q(x)\) uwe kazi nyingi. Hebu\(a\) kuwa idadi halisi. Kisha,
\[\lim_{x→a}p(x)=p(a) \nonumber \]
\[\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)} \nonumber \]
lini\(q(a)≠0\).
Ili kuona kwamba theorem hii inashikilia, fikiria polynomial
\[p(x)=c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0. \nonumber \]
Kwa kutumia jumla, mara kwa mara nyingi, na sheria za nguvu, tunaishia na
\[ \begin{align*} \lim_{x→a}p(x) &= \lim_{x→a}(c_nx^n+c_{n−1}x^{n−1}+⋯+c_1x+c_0) \\[4pt] &= c_n\left(\lim_{x→a}x\right)^n+c_{n−1}\left(\lim_{x→a}x\right)^{n−1}+⋯+c_1\left(\lim_{x→a}x\right)+\lim_{x→a}c_0 \\[4pt] &= c_na^n+c_{n−1}a^{n−1}+⋯+c_1a+c_0 \\[4pt] &= p(a) \end{align*}\]
Sasa ifuatavyo kutoka sheria quotient kwamba kama\(p(x)\) na\(q(x)\) ni polynomials ambayo\(q(a)≠0\),
basi
\[\lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}. \nonumber \]
Mfano\(\PageIndex{3}\): Evaluating a Limit of a Rational Function
Tathmini ya\(\displaystyle \lim_{x→3}\frac{2x^2−3x+1}{5x+4}\).
Suluhisho
Kwa kuwa 3 iko katika uwanja wa kazi ya busara\(f(x)=\displaystyle \frac{2x^2−3x+1}{5x+4}\), tunaweza kuhesabu kikomo kwa kubadili 3 kwa\(x\) kazi. Hivyo,
\[\lim_{x→3}\frac{2x^2−3x+1}{5x+4}=\frac{10}{19}. \nonumber \]
Zoezi\(\PageIndex{3}\)
Tathmini\(\displaystyle \lim_{x→−2}(3x^3−2x+7)\).
Matumizi ya mipaka ya POLYNOMIAL NA KAZI RATIONAL kama kumbukumbu
-13