2.2: Kikomo cha Kazi

Last updated
Save as PDF

Page ID: 178952

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Kutumia nukuu sahihi, kuelezea kikomo cha kazi.
Tumia meza ya maadili ili kukadiria kikomo cha kazi au kutambua wakati kikomo haipo.
Tumia grafu ili kukadiria kikomo cha kazi au kutambua wakati kikomo haipo.
Eleza mipaka ya upande mmoja na kutoa mifano.
Eleza uhusiano kati ya mipaka ya upande mmoja na mbili.
Kutumia notation sahihi, kuelezea kikomo usio na kipimo.
Eleza asymptote ya wima.

Dhana ya kikomo au mchakato wa kikomo, muhimu kwa uelewa wa calculus, imekuwa karibu kwa maelfu ya miaka. Kwa kweli, wanahisabati mapema walitumia mchakato wa kupunguza ili kupata makadirio bora na bora ya maeneo ya miduara. Hata hivyo, ufafanuzi rasmi wa kikomo—kama tunavyojua na kuielewa leo—haukuonekana mpaka mwishoni mwa karne ya 19. Kwa hiyo tunaanza jitihada zetu za kuelewa mipaka, kama mababu zetu wa hisabati walivyofanya, kwa kutumia mbinu ya angavu. Mwishoni mwa sura hii, wenye silaha na ufahamu wa dhana ya mipaka, tunachunguza ufafanuzi rasmi wa kikomo.

Tunaanza utafutaji wetu wa mipaka kwa kuangalia grafu za kazi

\(f(x)=\dfrac{x^2−4}{x−2}\),
\(g(x)=\dfrac{|x−2|}{x−2}\), na
\(h(x)=\dfrac{1}{(x−2)^2}\),

ambayo ni inavyoonekana katika Kielelezo\(\PageIndex{1}\). Hasa, hebu tuangalie mawazo yetu juu ya tabia ya kila grafu saa na karibu\(x=2\).

Grafu tatu za kazi. Ya kwanza ni f (s) = (x ^ 2 - 4)/(x-2), ambayo ni mstari wa mteremko, x intercept (-2,0), na mduara wazi katika (2,4). Ya pili ni g (x) = |x - 2 |/(x-2), ambayo ina mistari miwili: x=1 kwa x — Kielelezo\(\PageIndex{1}\): Grafu hizi zinaonyesha tabia ya kazi tatu tofauti kote\(x=2\).

Kila moja ya kazi tatu ni undefined katika\(x=2\), lakini kama sisi kufanya kauli hii na hakuna mwingine, sisi kutoa picha haujakamilika sana ya jinsi kila kazi tabia katika maeneo ya jirani ya\(x=2\). Ili kuelezea tabia ya kila grafu karibu na\(2\) zaidi kabisa, tunahitaji kuanzisha dhana ya kikomo.

Ufafanuzi wa Intuitive wa Kikomo

Hebu kwanza tuangalie kwa undani jinsi kazi\(f(x)=(x^2−4)/(x−2)\) inavyozunguka\(x=2\) kwenye Kielelezo\(\PageIndex{1}\). Kama maadili ya\(x\) mbinu\(2\) kutoka upande wowote wa\(2\), maadili ya\(y=f(x)\) mbinu\(4\). Kihisabati, tunasema kwamba kikomo cha\(f(x)\) kama\(x\) mbinu\(2\) ni\(4\). Symbolically, sisi kueleza kikomo hiki kama

\(\displaystyle \lim_{x \to 2} f(x)=4\).

Kutoka kwa kuangalia hii isiyo rasmi kwa kikomo kimoja, hebu tuanze kuendeleza ufafanuzi wa kisasa wa kikomo. Tunaweza kufikiria kikomo cha kazi kwa idadi\(a\) kama kuwa namba moja halisi\(L\) ambayo maadili ya kazi mbinu kama mbinu\(x\) -maadili\(a\), zinazotolewa idadi hiyo halisi\(L\) ipo. Alisema kwa makini zaidi, tuna ufafanuzi wafuatayo:

Ufafanuzi (Intuitive): Limit

Hebu\(f(x)\) kuwa kazi defined katika maadili yote katika muda wazi zenye\(a\), na ubaguzi iwezekanavyo ya\(a\) yenyewe, na hebu\(L\) kuwa idadi halisi. Ikiwa maadili yote ya kazi\(f(x)\) yanakaribia nambari halisi\(L\) kama maadili ya\(x(≠a)\) mbinu ya namba\(a\), basi tunasema kwamba kikomo cha\(f(x)\) kama\(x\) mbinu\(a\) ni\(L\). (Zaidi succinct, kama\(x\) anapata karibu na\(a\),\(f(x)\) anapata karibu na anakaa karibu na\(L\).) Symbolically, sisi kueleza wazo hili kama

\[\lim_{x \to a} f(x)=L. \label{limit} \]

Tunaweza kukadiria mipaka kwa kujenga meza za maadili ya kazi na kwa kuangalia grafu zao. Utaratibu huu umeelezwa katika Mkakati wa Kutatua Matatizo yafuatayo.

Mkakati wa Kutatua Matatizo: Kutathmini Kikomo Kutumia Jedwali la Maadili ya Kazi

1. Ili kutathmini\(\displaystyle \lim_{x \to a} f(x)\), tunaanza kwa kukamilisha meza ya maadili ya kazi. Tunapaswa kuchagua seti mbili ya\(x\) maadili - seti moja ya maadili inakaribia\(a\) na chini ya\(a\), na seti nyingine ya maadili inakaribia\(a\) na kubwa kuliko\(a\). Jedwali\(\PageIndex{1}\) linaonyesha nini meza yako inaweza kuonekana kama.

Jedwali\(\PageIndex{1}\)
\(x\)	\(f(x)\)	\(x\)	\(f(x)\)
\ (x\)” style="text-align:katikati; ">\(a-0.1\)	\ (f (x)\)” style="Nakala-align:center; ">\(f(a-0.1)\)	\ (x\)” style="text-align:katikati; ">\(a+0.1\)	\ (f (x)\)” style="Nakala-align:center; ">\(f(a+0.1)\)
\ (x\)” style="text-align:katikati; ">\(a-0.01\)	\ (f (x)\)” style="Nakala-align:center; ">\(f(a-0.01)\)	\ (x\)” style="text-align:katikati; ">\(a+0.01\)	\ (f (x)\)” style="Nakala-align:center; ">\(f(a+0.01)\)
\ (x\)” style="text-align:katikati; ">\(a-0.001\)	\ (f (x)\)” style="Nakala-align:center; ">\(f(a-0.001)\)	\ (x\)” style="text-align:katikati; ">\(a+0.001\)	\ (f (x)\)” style="Nakala-align:center; ">\(f(a+0.001)\)
\ (x\)” style="text-align:katikati; ">\(a-0.0001\)	\ (f (x)\)” style="Nakala-align:center; ">\(f(a-0.0001)\)	\ (x\)” style="text-align:katikati; ">\(a+0.0001\)	\ (f (x)\)” style="Nakala-align:center; ">\(f(a+0.0001)\)
\ (f (x)\)” rowspan="1" style="text-align:center; "> Tumia maadili ya ziada kama inavyohitajika.		\ (f (x)\)” rowspan="1" style="text-align:center; "> Tumia maadili ya ziada kama inavyohitajika.

2. Next, hebu angalia maadili katika kila\(f(x)\) nguzo na kuamua kama maadili kuonekana kuwa inakaribia thamani moja kama sisi hoja chini kila safu. Katika nguzo zetu, tunaangalia mlolongo\(f(a−0.1)\)\(f(a−0.01)\),\(f(a−0.001)\),\(f(a−0.0001)\),, na kadhalika\(f(a+0.1), \;f(a+0.01), \;f(a+0.001), \;f(a+0.0001)\), na kadhalika. (Kumbuka: Ingawa tumechagua\(x\) maadili\(a±0.1, \;a±0.01, \;a±0.001, \;a±0.0001\), na kadhalika, na maadili haya pengine kazi karibu kila wakati, katika hafla nadra sana tunaweza kuhitaji kurekebisha uchaguzi wetu.)

3. Ikiwa nguzo zote mbili\(y\) zinakaribia thamani ya kawaida\(L\), tunasema\(\displaystyle \lim_{x \to a}f(x)=L\). Tunaweza kutumia mkakati wafuatayo ili kuthibitisha matokeo yaliyopatikana kutoka meza au kama njia mbadala ya kukadiria kikomo.

4. Kutumia calculator graphing au programu ya kompyuta ambayo inaruhusu sisi kazi grafu\(f(x)\), tunaweza kupanga njama kazi, kuhakikisha maadili ya kazi ya\(f(x)\) kwa\(x\) -maadili karibu\(a\) ni katika dirisha yetu. Tunaweza kutumia kipengele kuwaeleza kwa hoja pamoja graph ya kazi na kuangalia\(y\) -value readout kama mbinu\(x\) -maadili\(a\). Ikiwa mbinu ya\(y\) maadili\(L\) kama mbinu zetu\(x\) za maadili\(a\) kutoka kwa pande zote mbili, basi\(\displaystyle \lim_{x \to a}f(x)=L\). Tunaweza kuhitaji kuvuta kwenye grafu yetu na kurudia mchakato huu mara kadhaa.

Tunatumia Mkakati huu wa Kutatua Matatizo kukokotoa kikomo katika Mifano\(\PageIndex{1A}\) na\(\PageIndex{1B}\).

Mfano\(\PageIndex{1A}\): Evaluating a Limit Using a Table of Functional Values

Tathmini\(\displaystyle \lim_{x \to 0}\frac{\sin x}{x}\) kutumia meza ya maadili ya kazi.

Suluhisho

Tumehesabu maadili ya maadili\(f(x)=\dfrac{\sin x}{x}\) ya\(x\) waliotajwa katika Jedwali\(\PageIndex{2}\).

Jedwali\(\PageIndex{2}\)
\(x\)	\(\frac{\sin x}{x}\)	\(x\)	\(\frac{\sin x}{x}\)
\ (x\)” style="text-align:katikati; "> -0.1	\ (\ frac {\ sin x} {x}\)” style="Nakala-align:katikati; "> 0.998334166468	\ (x\)” style="text-align:katikati; "> 0.1	\ (\ frac {\ sin x} {x}\)” style="Nakala-align:katikati; "> 0.998334166468
\ (x\)” style="Nakala-align:katikati; "> -0.01	\ (\ frac {\ sin x} {x}\)” style="Nakala-align:katikati; "> 0.999983333417	\ (x\)” style="text-align:katikati; "> 0.01	\ (\ frac {\ sin x} {x}\)” style="Nakala-align:katikati; "> 0.999983333417
\ (x\)” style="text-align:katikati; "> -0.001	\ (\ frac {\ sin x} {x}\)” style="Nakala-align:katikati; "> 0.999999833333	\ (x\)” style="text-align:katikati; "> 0.001	\ (\ frac {\ sin x} {x}\)” style="Nakala-align:katikati; "> 0.999999833333
\ (x\)” style="Nakala-align:katikati; "> -0.0001	\ (\ frac {\ sin x} {x}\)” style="Nakala-align:katikati; "> 0.999999998333	\ (x\)” style="Nakala-align:katikati; "> 0.0001	\ (\ frac {\ sin x} {x}\)” style="Nakala-align:katikati; "> 0.999999998333

Kumbuka: Maadili katika meza hii yalipatikana kwa kutumia calculator na kutumia maeneo yote yaliyotolewa katika pato la calculator.

Tunaposoma chini kila\(\dfrac{\sin x}{x}\) safu, tunaona kwamba maadili katika kila safu yanaonekana kuwa inakaribia moja. Hivyo, ni busara kuhitimisha hilo\(\displaystyle \lim_{x\to0}\frac{\sin x}{x}=1\). Calculator-au kompyuta-yanayotokana graph ya\(f(x)=\dfrac{\sin x}{x}\) itakuwa sawa na ile inavyoonekana katika Kielelezo\(\PageIndex{2}\), na inathibitisha makadirio yetu.

Grafu ya f (x) = dhambi (x) /x juu ya muda [-6, 6]. Kazi ya curving ina y intercept katika x = 0 na x intercepts katika y = pi na y = -pi. — Kielelezo\(\PageIndex{2}\): Grafu ya\(f(x)=(\sin x)/x\) inathibitisha makadirio kutoka Jedwali\(\PageIndex{2}\).

Mfano\(\PageIndex{1B}\): Evaluating a Limit Using a Table of Functional Values

Tathmini\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}\) kutumia meza ya maadili ya kazi.

Suluhisho

Kama kabla, sisi kutumia meza-katika kesi hii, Jedwali\(\PageIndex{3}\) - kuorodhesha maadili ya kazi kwa maadili fulani ya\(x\).

Jedwali\(\PageIndex{3}\)
\(x\)	\(\frac{\sqrt{x}−2}{x−4}\)	\(x\)	\(\frac{\sqrt{x}−2}{x−4}\)
\ (x\)” style="text-align:katikati; "> 3.9	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.251582341869	\ (x\)” style="text-align:katikati; "> 4.1	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.248456731317
\ (x\)” style="text-align:katikati; "> 3.99	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.25015644562	\ (x\)” style="text-align:katikati; "> 4.01	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.24984394501
\ (x\)” style="Nakala-align:katikati; "> 3.999	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.250015627	\ (x\)” style="text-align:katikati; "> 4.001	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.249984377
\ (x\)” style="Nakala-align:katikati; "> 3.9999	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.250001563	\ (x\)” style="Nakala-align:katikati; "> 4.0001	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.249998438
\ (x\)” style="Nakala-align:katikati; "> 3.99999	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.25000016	\ (x\)” style="text-align:katikati; "> 4.00001	\ (\ frac {\ sqrt {x} -1} {x-4}\)” style="Nakala-align:katikati; "> 0.24999984

Baada ya kuchunguza meza hii, tunaona kwamba maadili ya kazi chini ya 4 yanaonekana kupungua kuelekea 0.25 wakati maadili ya kazi zaidi ya 4 yanaonekana yanaongezeka kuelekea 0.25. Tunahitimisha kuwa\(\displaystyle \lim_{x\to4}\frac{\sqrt{x}−2}{x−4}=0.25\). Sisi kuthibitisha makadirio haya kwa kutumia grafu ya\(f(x)=\dfrac{\sqrt{x}−2}{x−4}\) inavyoonekana katika Kielelezo\(\PageIndex{3}\).

Grafu ya kazi f (x) = (sqrt (x) - 2)/(x-4) juu ya muda [0,8]. Kuna mduara wazi juu ya kazi katika x=4. Kazi curves asymptotically kuelekea mhimili x na y mhimili katika quadrant moja. — Kielelezo\(\PageIndex{3}\): Grafu ya\(\frac{\sqrt{x}−2}{x−4}\) inathibitisha makadirio kutoka Jedwali\(\PageIndex{3}\).

Zoezi\(\PageIndex{1}\)

Tathmini\(\displaystyle \lim_{x \to 1} \frac{\frac{1}{x}−1}{x−1}\) kutumia meza ya maadili ya kazi. Tumia grafu ili kuthibitisha makadirio yako.

Kidokezo: Tumia 0.9, 0.99, 0.999, 0.9999, 0.99999 na 1.1, 1.01, 1.001, 1.0001, 1.00001 kama maadili yako ya meza.
Jibu: \[\lim_{x\to1}\frac{\frac{1}{x}−1}{x−1}=−1\nonumber \]

Katika hatua hii, tunaona kutoka Mifano\(\PageIndex{1A}\) na\(\PageIndex{1b}\) kwamba inaweza kuwa rahisi, ikiwa si rahisi, kukadiria kikomo cha kazi kwa kuchunguza grafu yake kama ilivyo kukadiria kikomo kwa kutumia meza ya maadili ya kazi. Katika Mfano\(\PageIndex{2}\), tunatathmini kikomo pekee kwa kuangalia grafu badala ya kutumia meza ya maadili ya kazi.

Mfano\(\PageIndex{2}\): Evaluating a Limit Using a Graph

Kwa\(g(x)\) inavyoonekana katika Kielelezo\(\PageIndex{4}\), tathmini\(\displaystyle \lim_{x\to−1}g(x)\).

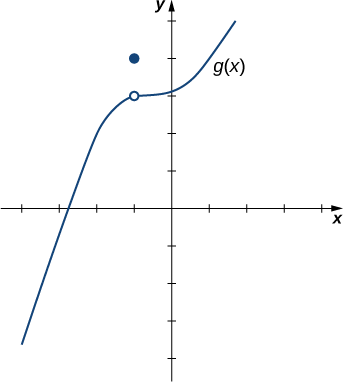
Grafu ya kazi ya kupigia generic g (x). Katika roboduara mbili, kuna mduara wazi juu ya kazi katika (-1,3) na mduara imefungwa kitengo moja hadi saa (-1, 4). — Kielelezo\(\PageIndex{4}\): Grafu ya\(g(x)\) inajumuisha thamani moja sio kwenye safu ya laini.

Suluhisho:

Pamoja na ukweli kwamba\(g(−1)=4\), kama njia ya\(x\) maadili\(−1\) kutoka upande wowote, mbinu za\(g(x)\) maadili\(3\). Kwa hiyo,\(\displaystyle \lim_{x\to−1}g(x)=3\). Kumbuka kwamba tunaweza kuamua kikomo hiki bila hata kujua usemi wa algebraic wa kazi.

Kulingana na Mfano\(\PageIndex{2}\), tunafanya uchunguzi wafuatayo: Inawezekana kwa kikomo cha kazi kuwepo kwa hatua, na kwa kazi inayoelezwa kwa hatua hii, lakini kikomo cha kazi na thamani ya kazi katika hatua inaweza kuwa tofauti.

Zoezi\(\PageIndex{2}\)

Tumia grafu ya\(h(x)\) katika Kielelezo\(\PageIndex{5}\) ili kutathmini\(\displaystyle \lim_{x \to 2}h(x)\), ikiwa inawezekana.

Grafu ya kazi h (x), ambayo ni parabola iliyowekwa juu ya [-2.5, 5]. Kuna mduara wazi ambapo vertex inapaswa kuwa katika hatua (2, -1). — Kielelezo\(\PageIndex{5}\):

Kidokezo: Nini\(y\) -thamani gani kazi mbinu kama mbinu\(x\) -maadili\(2\)?
Suluhisho: \(\displaystyle \lim_{x \to 2}h(x)=−1.\)

Kuangalia meza ya maadili ya kazi au kuangalia grafu ya kazi hutupa ufahamu muhimu katika thamani ya kikomo cha kazi katika hatua fulani. Hata hivyo, mbinu hizi zinategemea sana juu ya guesswork. Hatimaye tunahitaji kuendeleza mbinu mbadala za kutathmini mipaka. Mbinu hizi mpya ni zaidi ya algebraic katika asili na tunazichunguza katika sehemu inayofuata; hata hivyo, katika hatua hii tunaanzisha mipaka miwili maalum ambayo ni msingi kwa mbinu zijazo.

Mipaka miwili muhimu

Hebu\(a\) kuwa namba halisi na\(c\) uwe mara kwa mara.

\(\displaystyle \lim_{x \to a}x=a\)
\(\displaystyle \lim_{x \to a}c=c\)

Tunaweza kufanya uchunguzi zifuatazo kuhusu mipaka hii miwili.

Kwa kikomo cha kwanza, angalia kwamba kama\(x\) mbinu\(a\), hivyo\(f(x)\), kwa sababu\(f(x)=x\). Kwa hiyo,\(\displaystyle \lim_{x \to a}x=a\).
Kwa kikomo cha pili, fikiria Jedwali\(\PageIndex{4}\).

Jedwali\(\PageIndex{4}\)
\(x\)	\(f(x)=c\)	\(x\)	\(f(x)=c\)
\ (x\)” style="text-align:katikati; ">\(a-0.1\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)	\ (x\)” style="text-align:katikati; ">\(a+0.1\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)
\ (x\)” style="text-align:katikati; ">\(a-0.01\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)	\ (x\)” style="text-align:katikati; ">\(a+0.01\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)
\ (x\)” style="text-align:katikati; ">\(a-0.001\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)	\ (x\)” style="text-align:katikati; ">\(a+0.001\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)
\ (x\)” style="text-align:katikati; ">\(a-0.0001\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)	\ (x\)” style="text-align:katikati; ">\(a+0.0001\)	\ (f (x) =c\)” style="text-align:center; ">\(c\)

Angalia kwamba kwa maadili yote ya\(x\) (bila kujali kama yanakaribia\(a\)), maadili\(f(x)\) hubakia mara kwa mara\(c\). Hatuna chaguo bali kuhitimisha\(\displaystyle \lim_{x \to a}c=c\).

Kuwepo kwa Limit

Kama tunaona kikomo katika mfano unaofuata, kukumbuka kwamba kwa kikomo cha kazi kuwepo katika hatua, maadili ya kazi lazima mbinu moja thamani halisi ya idadi katika hatua hiyo. Ikiwa maadili ya kazi hayakukaribia thamani moja, basi kikomo haipo.

Mfano\(\PageIndex{3}\): Evaluating a Limit That Fails to Exist

Tathmini\(\displaystyle\lim_{x \to 0}\sin(1/x)\) kutumia meza ya maadili.

Suluhisho

Meza\(\PageIndex{5}\) orodha maadili kwa ajili ya kazi\(\sin(1/x)\) kwa ajili ya maadili kutokana na\(x\).

Jedwali\(\PageIndex{5}\)
\(x\)	\(\sin(1/x)\)	\(x\)	\(\sin(1/x)\)
\ (x\)” style="text-align:katikati; "> -0.1	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> 0.544021110889	\ (x\)” style="text-align:katikati; "> 0.1	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> -0.544021110889
\ (x\)” style="Nakala-align:katikati; "> -0.01	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> 0.50636564111	\ (x\)” style="text-align:katikati; "> 0.01	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> -0.50636564111
\ (x\)” style="text-align:katikati; "> -0.001	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> -0.8268795405312	\ (x\)” style="text-align:katikati; "> 0.001	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> 0.8268795405312
\ (x\)” style="Nakala-align:katikati; "> -0.0001	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> 0.305614388888	\ (x\)” style="Nakala-align:katikati; "> 0.0001	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> -0.305614388888
\ (x\)” style="text-align:katikati; "> -0.00001	\ (\ dhambi (1/x)\)” style="text-align:katikati; "> -0.0357487987	\ (x\)” style="text-align:katikati; "> 0.00001	\ (\ dhambi (1/x)\)” style="text-align:katikati; "> 0.0357487987
\ (x\)” style="text-align:katikati; "> -0.000001	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> 0.349993504187	\ (x\)” style="text-align:katikati; "> 0.000001	\ (\ dhambi (1/x)\)” style="Nakala-align:katikati; "> -0.349993504187

Baada ya kuchunguza meza ya maadili ya kazi, tunaweza kuona kwamba\(y\) -maadili hayaonekani kufikia thamani yoyote moja. Inaonekana kikomo haipo. Kabla ya kuchora hitimisho hili, hebu tuchukue mbinu zaidi ya utaratibu. Chukua mlolongo wafuatayo wa\(x\) -maadili inakaribia\(0\):

\[\frac{2}{π},\;\frac{2}{3π},\;\frac{2}{5π},\;\frac{2}{7π},\;\frac{2}{9π},\;\frac{2}{11π},\;….\nonumber \]

\(y\)Maadili ya sambamba ni

\[1,\;-1,\;1,\;-1,\;1,\;-1,\;....\nonumber \]

Katika hatua hii tunaweza kweli kuhitimisha kwamba\(\displaystyle \lim_{x \to 0} \sin(1/x)\) haipo. (Wanahisabati mara nyingi hufupisha “haipo” kama DNE. Hivyo, tunataka kuandika\(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE.) Grafu ya\(f(x)=\sin(1/x)\) inavyoonekana katika Kielelezo\(\PageIndex{6}\) na inatoa picha wazi ya tabia ya\(\sin(1/x)\) kama\(x\) mbinu\(0\). Unaweza kuona kwamba\(\sin(1/x)\) oscillates milele zaidi wildly kati\(−1\) na\(1\) kama\(x\) mbinu\(0\).

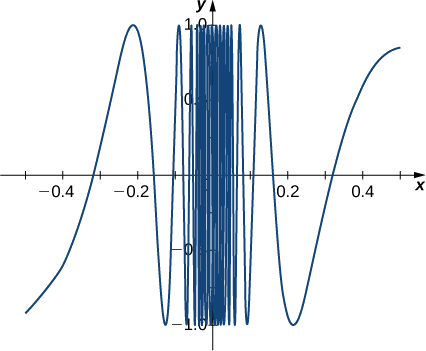
Grafu ya kazi f (x) = dhambi (1/x), ambayo oscillates haraka kati ya -1 na 1 kama x inakaribia 0. Kufuta ni mara kwa mara kama kazi inakwenda mbali na 0 kwenye mhimili wa x. — Kielelezo\(\PageIndex{6}\): Grafu ya\(f(x)=\sin (1/x)\) oscillates haraka kati\(−1\) na\(1\) kama\(x\) mbinu\(0\).

Zoezi\(\PageIndex{3}\)

Tumia meza ya maadili ya kazi ili kutathmini\(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\), ikiwa inawezekana.

Kidokezo: Matumizi\(x\) -maadili 1.9, 1.99, 1.999, 1.9999, 1.99999 na 2.1, 2.01, 2.001, 2.0001, 2.00001 katika meza yako.
Jibu: \(\displaystyle \lim_{x \to 2}\frac{∣x^2−4∣}{x−2}\)haipo.

Mipaka ya upande mmoja

Wakati mwingine kuonyesha kwamba kikomo cha kazi kinashindwa kuwepo kwa hatua haitupatia taarifa za kutosha kuhusu tabia ya kazi katika hatua hiyo. Ili kuona hili, sasa tunatazama tena kazi\(g(x)=|x−2|/(x−2)\) iliyoletwa mwanzoni mwa sehemu (angalia Mchoro\(\PageIndex{1}\) (b)). Kama sisi kuchukua maadili ya\(x\) karibu na\(2\),\(g(x)\) haina mbinu thamani moja, hivyo kikomo kama\(x\) mbinu\(2\) haipo - yaani,\(\displaystyle \lim_{x \to 2}g(x)\) DNE. Hata hivyo, kauli hii peke yake haina kutupa picha kamili ya tabia ya kazi karibu\(x\) -thamani\(2\). Ili kutoa maelezo sahihi zaidi, tunaanzisha wazo la kikomo cha upande mmoja. Kwa maadili yote upande wa kushoto wa\(2\) (au upande hasi wa\(2\)),\(g(x)=−1\). Hivyo, kama\(x\) mbinu\(2\) kutoka upande wa kushoto,\(g(x)\) mbinu\(−1\). Kihisabati, tunasema kwamba kikomo kama\(x\) mbinu\(2\) kutoka kushoto ni\(−1\). Symbolically, sisi kueleza wazo hili kama

\[\lim_{x \to 2^−}g(x)=−1. \nonumber \]

Vile vile, kama\(x\) mbinu\(2\) kutoka kwa haki (au kutoka upande mzuri),\(g(x)\) hukaribia\(1\). Symbolically, sisi kueleza wazo hili kama

\[\lim_{x \to 2^+}g(x)=1.\nonumber \]

Sasa tunaweza kuwasilisha ufafanuzi usio rasmi wa mipaka ya upande mmoja.

Ufafanuzi: Mipaka ya upande mmoja

Tunafafanua aina mbili za mipaka ya upande mmoja.

Punguza kutoka upande wa kushoto:

Hebu\(f(x)\) kuwa kazi defined katika maadili yote katika muda wazi wa fomu\((z,a)\), na hebu\(L\) kuwa idadi halisi. Ikiwa maadili ya kazi\(f(x)\) yanakaribia namba halisi\(L\) kama maadili ya\(x\) (wapi\(x<a\)) inakaribia nambari\(a\), basi tunasema kwamba\(L\) ni kikomo cha\(f(x)\) kama\(x\) mbinu\(a\) kutoka upande wa kushoto. Symbolically, sisi kueleza wazo hili kama

\[\lim_{x \to a^−}f(x)=L. \nonumber \]

Punguza kutoka kulia:

Hebu\(f(x)\) kuwa kazi defined katika maadili yote katika muda wazi wa fomu\((a,c)\), na hebu\(L\) kuwa idadi halisi. Ikiwa maadili ya kazi\(f(x)\) yanakaribia namba halisi\(L\) kama maadili ya\(x\) (wapi\(x>a\)) inakaribia nambari\(a\), basi tunasema kwamba\(L\) ni kikomo cha\(f(x)\) kama\(x\) mbinu\(a\) kutoka kulia. Symbolically, sisi kueleza wazo hili kama

\[\lim_{x \to a^+}f(x)=L. \nonumber \]

Mfano\(\PageIndex{4}\): Evaluating One-Sided Limits

Kwa kazi\(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\), tathmini kila moja ya mipaka ifuatayo.

\(\displaystyle \lim_{x \to 2^−}f(x)\)
\(\displaystyle \lim_{x \to 2^+}f(x)\)

Suluhisho

Tunaweza kutumia meza ya maadili ya kazi tena. Angalia katika Jedwali\(\PageIndex{6}\) kwamba kwa maadili ya\(x\) chini\(2\), tunatumia\(f(x)=x+1\) na kwa maadili ya\(x\) zaidi kuliko\(2\), tunatumia\(f(x)=x^2−4.\)

Jedwali\(\PageIndex{6}\)
\(x\)	\(f(x)=x+1\)	\(x\)	\(f(x)=x^2-4\)
\ (x\)” style="text-align:katikati; "> 1.9	\ (f (x) =x+1\)” style="text-align:katikati; "> 2.9	\ (x\)” style="text-align:katikati; "> 2.1	\ (f (x) =x^2-4\)” style="text-align:katikati; "> 0.41
\ (x\)” style="text-align:katikati; "> 1.99	\ (f (x) =x+1\)” style="text-align:katikati; "> 2.99	\ (x\)” style="text-align:katikati; "> 2.01	\ (f (x) =x^2-4\)” style="text-align:katikati; "> 0.0401
\ (x\)” style="Nakala-align:katikati; "> 1.999	\ (f (x) =x+1\)” style="text-align:katikati; "> 2.999	\ (x\)” style="text-align:katikati; "> 2.001	\ (f (x) =x^2-4\)” style="text-align:katikati; "> 0.004001
\ (x\)” style="Nakala-align:katikati; "> 1.9999	\ (f (x) =x+1\)” style="text-align:katikati; "> 2.9999	\ (x\)” style="Nakala-align:katikati; "> 2.0001	\ (f (x) =x^2-4\)” style="text-align:katikati; "> 0.00040001
\ (x\)” style="Nakala-align:katikati; "> 1.99999	\ (f (x) =x+1\)” style="text-align:katikati; "> 2.99999	\ (x\)” style="text-align:katikati; "> 2.00001	\ (f (x) =x^2-4\)” style="text-align:katikati; "> 0.0000400001

Kulingana na meza hii, tunaweza kuhitimisha kuwa a.\(\displaystyle \lim_{x \to 2^−}f(x)=3\) na b\(\displaystyle \lim_{x \to 2^+}f(x)=0\). Kwa hiyo, kikomo cha (mbili-upande mmoja) cha\(f(x)\) haipo\(x=2\). Kielelezo\(\PageIndex{7}\) kinaonyesha grafu ya\(f(x)\) na kuimarisha hitimisho letu kuhusu mipaka hii.

Grafu ya kazi iliyopewa kipande. Kipande cha kwanza ni f (x) = x+1 ikiwa x <2. Kipande cha pili ni x^2 - 4 ikiwa x — Kielelezo\(\PageIndex{7}\): Grafu ya\(f(x)=\begin{cases}x+1, & \text{if }x<2\\ x^2−4, & \text{if }x≥2\end{cases}\) ina mapumziko saa\(x=2\).

Zoezi\(\PageIndex{4}\)

Tumia meza ya maadili ya kazi ili kukadiria mipaka ifuatayo, ikiwa inawezekana.

\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\)
\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}\)

Kidokezo

Matumizi\(x\) -maadili 1.9, 1.99, 1.999, 1.9999, 1.99999 kukadiria\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}\).

\(x\)Tumia maadili 2.1, 2.01, 2.001, 2.0001, 2.00001 ili kukadiria\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}.\)

(Meza hizi zinapatikana kutoka tatizo uliopita Checkpoint.)

Suluhisho a

a.\(\displaystyle \lim_{x→2^−}\frac{∣x^2−4∣}{x−2}=−4\)

Suluhisho b

\(\displaystyle \lim_{x→2^+}\frac{∣x^2−4∣}{x−2}=4\)

Hebu sasa fikiria uhusiano kati ya kikomo cha kazi katika hatua na mipaka kutoka kulia na kushoto katika hatua hiyo. Inaonekana wazi kwamba ikiwa kikomo kutoka kulia na kikomo kutoka kushoto kina thamani ya kawaida, basi thamani ya kawaida ni kikomo cha kazi wakati huo. Vile vile, ikiwa kikomo kutoka upande wa kushoto na kikomo kutoka kwa haki huchukua maadili tofauti, kikomo cha kazi haipo. Hitimisho hizi ni muhtasari katika Kumbuka.

Kuhusiana na Mipaka ya Upande mmoja na Mbili

Hebu\(f(x)\) kuwa kazi defined katika maadili yote katika muda wazi zenye\(a\), na ubaguzi iwezekanavyo ya\(a\) yenyewe, na hebu\(L\) kuwa idadi halisi. Kisha,

\[\lim_{x \to a}f(x)=L \nonumber \]

kama na tu kama\(\displaystyle \lim_{x \to a^−}f(x)=L\) na\(\displaystyle \lim_{x \to a^+} f(x)=L\).

mipaka usio

Kutathmini kikomo cha kazi katika hatua au kutathmini kikomo cha kazi kutoka kulia na kushoto katika hatua inatusaidia tabia tabia ya kazi karibu thamani fulani. Kama tutakavyoona, tunaweza pia kuelezea tabia ya kazi ambazo hazina mipaka ya mwisho.

Sasa tunageuka mawazo yetu\(h(x)=1/(x−2)^2\), kazi ya tatu na ya mwisho ilianzishwa mwanzoni mwa sehemu hii (angalia Mchoro\(\PageIndex{1}\) (c)). Kutoka kwenye grafu yake tunaona kwamba kama maadili ya\(x\) mbinu\(2\), maadili ya\(h(x)=1/(x−2)^2\) kuwa makubwa na makubwa na, kwa kweli, kuwa usio na kipimo. Kihisabati, tunasema kwamba kikomo cha\(h(x)\) kama\(x\) mbinu\(2\) ni infinity chanya. Symbolically, sisi kueleza wazo hili kama

\[\lim_{x \to 2}h(x)=+∞. \nonumber \]

Zaidi kwa ujumla, sisi kufafanua mipaka usio kama ifuatavyo:

ufafanuzi: mipaka isiyo na mwisho

Tunafafanua aina tatu za mipaka isiyo na kipimo.

mipaka usio na mwisho kutoka upande wa kushoto: Hebu\(f(x)\) kuwa kazi defined katika maadili yote katika muda wazi wa fomu\((b,a)\).

i Ikiwa maadili ya\(f(x)\) ongezeko bila kufungwa kama maadili ya\(x\) (wapi\(x<a\)) inakaribia idadi\(a\), basi tunasema kuwa kikomo kama\(x\) mbinu\(a\) kutoka upande wa kushoto ni infinity chanya na tunaandika\[\lim_{x \to a^−}f(x)=+∞. \nonumber \]

ii. Ikiwa maadili ya\(f(x)\) kupungua bila kufungwa kama maadili ya\(x\) (wapi\(x<a\)) yanakaribia namba\(a\), basi tunasema kuwa kikomo kama\(x\) mbinu\(a\) kutoka upande wa kushoto ni usio na mwisho na tunaandika\[\lim_{x \to a^−}f(x)=−∞. \nonumber \]

mipaka usio na mwisho kutoka kulia: Hebu\(f(x)\) kuwa kazi defined katika maadili yote katika muda wazi wa fomu\((a,c)\).

i Ikiwa maadili ya\(f(x)\) ongezeko bila kufungwa kama maadili ya\(x\) (wapi\(x>a\)) inakaribia idadi\(a\), basi tunasema kuwa kikomo kama\(x\) mbinu\(a\) kutoka kwa haki ni infinity chanya na tunaandika\[\lim_{x \to a^+}f(x)=+∞. \nonumber \]

ii. Ikiwa maadili ya\(f(x)\) kupungua bila kufungwa kama maadili ya\(x\) (wapi\(x>a\)) yanakaribia namba\(a\), basi tunasema kuwa kikomo kama\(x\) mbinu\(a\) kutoka kwa haki ni infinity hasi na tunaandika\[\lim_{x \to a^+}f(x)=−∞. \nonumber \]

Mbili upande usio kikomo: Hebu\(f(x)\) defined kwa wote\(x≠a\) katika kipindi wazi zenye\(a\)

i Kama maadili ya\(f(x)\) ongezeko bila kufungwa kama maadili ya\(x\) (wapi\(x≠a\)) inakaribia idadi\(a\), basi tunasema kuwa kikomo kama\(x\) mbinu\(a\) ni infinity chanya na tunaandika\[\lim_{x \to a} f(x)=+∞. \nonumber \]

ii. Ikiwa maadili ya\(f(x)\) kupungua bila kufungwa kama maadili ya\(x\) (wapi\(x≠a\)) yanakaribia namba\(a\), basi tunasema kuwa kikomo kama\(x\) mbinu\(a\) ni infinity hasi na tunaandika\[\lim_{x \to a}f(x)=−∞. \nonumber \]

Ni muhimu kuelewa kwamba wakati sisi kuandika kauli kama vile\(\displaystyle \lim_{x \to a}f(x)=+∞\) au\(\displaystyle \lim_{x \to a}f(x)=−∞\) sisi ni kuelezea tabia ya kazi, kama sisi tu defined yake. Sisi si akidai kuwa kikomo ipo. Kwa kikomo cha kazi\(f(x)\) kuwepo katika\(a\), ni lazima mbinu idadi halisi\(L\) kama\(x\) mbinu\(a\). Hiyo ilisema, kama, kwa mfano\(\displaystyle \lim_{x \to a}f(x)=+∞\), sisi daima kuandika\(\displaystyle \lim_{x \to a}f(x)=+∞\) badala ya\(\displaystyle \lim_{x \to a}f(x)\) DNE.

Mfano\(\PageIndex{5}\): Recognizing an Infinite Limit

Tathmini kila moja ya mipaka ifuatayo, ikiwa inawezekana. Tumia meza ya maadili ya kazi na grafu\(f(x)=1/x\) ili kuthibitisha hitimisho lako.

\(\displaystyle \lim_{x \to 0^−} \frac{1}{x}\)
\(\displaystyle \lim_{x \to 0^+} \frac{1}{x}\)
\( \displaystyle \lim_{x \to 0}\frac{1}{x}\)

Suluhisho

Anza kwa kujenga meza ya maadili ya kazi.

Jedwali\(\PageIndex{7}\)
\(x\)	\(\dfrac{1}{x}\)	\(x\)	\(\dfrac{1}{x}\)
\ (x\)” style="text-align:katikati; "> -0.1	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; ">-10	\ (x\)” style="text-align:katikati; "> 0.1	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; "> 10
\ (x\)” style="Nakala-align:katikati; "> -0.01	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; ">-100	\ (x\)” style="text-align:katikati; "> 0.01	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; "> 100
\ (x\)” style="text-align:katikati; "> -0.001	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; ">-1000	\ (x\)” style="text-align:katikati; "> 0.001	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; "> 1000
\ (x\)” style="Nakala-align:katikati; "> -0.0001	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; ">-10,000	\ (x\)” style="Nakala-align:katikati; "> 0.0001	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; "> 10,000
\ (x\)” style="text-align:katikati; "> -0.00001	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; "> -100,000	\ (x\)” style="text-align:katikati; "> 0.00001	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; "> 100,000
\ (x\)” style="text-align:katikati; "> -0.000001	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; ">-1,000,000	\ (x\)” style="text-align:katikati; "> 0.000001	\ (\ dfrac {1} {x}\)” style="Nakala-align:katikati; "> 1,000,000

a. maadili ya\(1/x\) kupungua bila kufungwa kama\(x\) mbinu\(0\) kutoka kushoto. Sisi kuhitimisha kwamba

\[\lim_{x \to 0^−}\frac{1}{x}=−∞.\nonumber \]

b. maadili ya\(1/x\) ongezeko bila kufungwa kama\(x\) mbinu\(0\) kutoka kulia. Sisi kuhitimisha kwamba

\[\lim_{x \to 0^+}\frac{1}{x}=+∞. \nonumber \]

c Tangu\(\displaystyle \lim_{x \to 0^−}\frac{1}{x}=−∞\) na\(\displaystyle \lim_{x \to 0^+}\frac{1}{x}=+∞\) kuwa na maadili tofauti, tunahitimisha kuwa

\[\lim_{x \to 0}\frac{1}{x}\quad\text{DNE.} \nonumber \]

Grafu ya\(f(x)=1/x\) katika Kielelezo\(\PageIndex{8}\) inathibitisha hitimisho hizi.

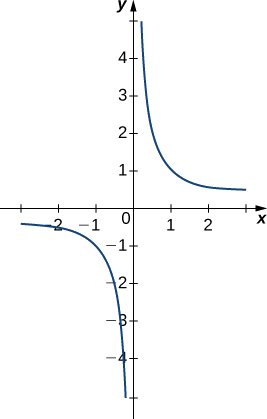
Grafu ya kazi f (x) = 1/x. kazi curves asymptotically kuelekea x=0 na y = 0 katika quadrants moja na tatu. — Kielelezo\(\PageIndex{8}\): Grafu ya\(f(x)=1/x\) inathibitisha kwamba kikomo kama\(x\) mbinu\(0\) haipo.

Zoezi\(\PageIndex{5}\)

Tathmini kila moja ya mipaka ifuatayo, ikiwa inawezekana. Tumia meza ya maadili ya kazi na grafu\(f(x)=1/x^2\) ili kuthibitisha hitimisho lako.

\(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}\)
\(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}\)
\(\displaystyle \lim_{x \to 0}\frac{1}{x^2}\)

Kidokezo

Fuata taratibu kutoka Mfano\(\PageIndex{5}\).

Jibu

a\(\displaystyle \lim_{x \to 0^−}\frac{1}{x^2}=+∞\);.

b\(\displaystyle \lim_{x \to 0^+}\frac{1}{x^2}=+∞\);

c.\(\displaystyle \lim_{x \to 0}\frac{1}{x^2}=+∞\)

Ni muhimu kusema kwamba kazi ya fomu\(f(x)=1/(x−a)^n\), ambapo n ni integer chanya, na mipaka usio kama\(x\) mbinu\(a\) kutoka ama kushoto au kulia (Kielelezo\(\PageIndex{9}\)). Mipaka hii ni muhtasari katika ufafanuzi hapo juu.

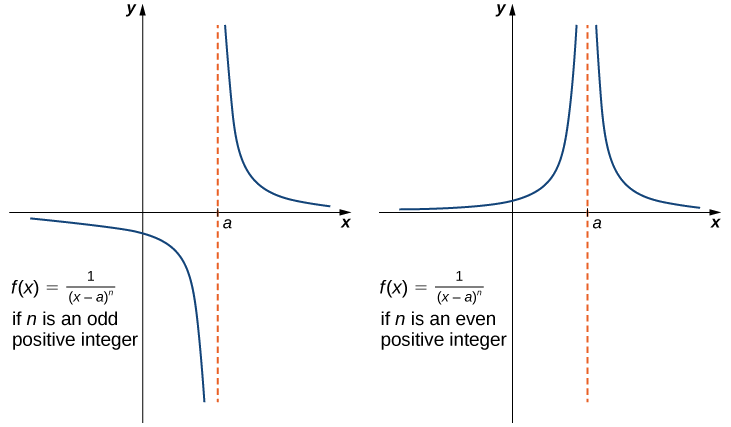
Grafu mbili upande upande wa f (x) = 1/(x-a) ^n. graph kwanza inaonyesha kesi ambapo n ni isiyo ya kawaida chanya integer, na pili inaonyesha kesi ambapo n ni integer hata chanya. Katika kwanza, grafu ina makundi mawili. Kila Curve asymptotically kuelekea mhimili x, pia inajulikana kama y = 0, na x=a. sehemu upande wa kushoto wa x=a ni chini ya mhimili x, na sehemu ya haki ya x=a ni juu ya mhimili x. Katika grafu ya pili, makundi yote ni juu ya mhimili x. — Kielelezo\(\PageIndex{9}\): kazi\(f(x)=1/(x−a)^n\) ina mipaka usio katika\(a\).

Mipaka isiyo na mwisho kutoka kwa integers Chanya

Ikiwa\(n\) ni chanya hata integer, basi

\[\lim_{x \to a}\frac{1}{(x−a)^n}=+∞.\label{infLim1} \]

Kama\(n\) ni chanya isiyo ya kawaida integer, basi

\[\lim_{x \to a^+}\frac{1}{(x−a)^n}=+∞\label{infLim2} \]

\[\lim_{x \to a^−}\frac{1}{(x−a)^n}=−∞.\label{infLim3} \]

Tunapaswa pia kusema kwamba katika grafu ya\(f(x)=1/(x−a)^n\), pointi kwenye grafu kuwa\(x\) -kuratibu karibu sana na\(a\) ni karibu sana na mstari wima\(x=a\). Hiyo ni, kama\(x\) mbinu\(a\), pointi kwenye grafu ya\(f(x)\) ni karibu na mstari\(x=a\). Mstari\(x=a\) huitwa asymptote ya wima ya grafu. Sisi rasmi kufafanua asymptote wima kama ifuatavyo:

Ufafanuzi: Asymptotes ya wima

Hebu\(f(x)\) kuwa kazi. Ikiwa mojawapo ya masharti yafuatayo yanashikilia, basi mstari\(x=a\) ni asymptote ya wima ya\(f(x)\).

\[\lim_{x \to a^−}f(x)=+∞ \nonumber \]

\[\lim_{x \to a^−}f(x)=−∞ \nonumber \]

\[\lim_{x \to a^+}f(x)=+∞ \nonumber \]

\[\lim_{x \to a^+}f(x)=−∞ \nonumber \]

\[\lim_{x \to a}f(x)=+∞ \nonumber \]

\[\lim_{x \to a}f(x)=−∞ \nonumber \]

Mfano\(\PageIndex{6}\): Finding a Vertical Asymptote

Tathmini kila moja ya mipaka ifuatayo kwa kutumia equations\ ref {InFlim1},\ ref {InFlim2}, na\ ref {InFlim3} hapo juu. Tambua asymptotes yoyote ya wima ya kazi\(f(x)=1/(x+3)^4.\)

\(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}\)
\(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}\)
\(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}\)

Suluhisho

Tunaweza kutumia equations hapo juu moja kwa moja.

\(\displaystyle \lim_{x \to −3^−}\frac{1}{(x+3)^4}=+∞\)
\(\displaystyle \lim_{x \to −3^+}\frac{1}{(x+3)^4}=+∞\)
\(\displaystyle \lim_{x \to −3}\frac{1}{(x+3)^4}=+∞\)

kazi\(f(x)=1/(x+3)^4\) ina asymptote wima ya\(x=−3\).

Zoezi\(\PageIndex{6}\)

Tathmini kila moja ya mipaka ifuatayo. Tambua asymptotes yoyote ya wima ya kazi\(f(x)=\dfrac{1}{(x−2)^3}\).

\(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}\)
\(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}\)
\(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)

Jibu: \(\displaystyle \lim_{x→2^−}\frac{1}{(x−2)^3}=−∞\)
Jibu b: \(\displaystyle \lim_{x→2^+}\frac{1}{(x−2)^3}=+∞\)
Jibu c: \(\displaystyle \lim_{x→2}\frac{1}{(x−2)^3}\)DNE. Mstari\(x=2\) ni asymptote ya wima\(f(x)=1/(x−2)^3.\)

Katika mfano unaofuata tunaweka ujuzi wetu wa aina mbalimbali za mipaka ya kutumia kuchambua tabia ya kazi katika pointi kadhaa tofauti.

Mfano\(\PageIndex{7}\): Behavior of a Function at Different Points

Tumia grafu ya\(f(x)\) katika Kielelezo\(\PageIndex{10}\) kuamua kila moja ya maadili yafuatayo:

\(\displaystyle \lim_{x \to −4^−}f(x)\);\(\displaystyle \lim_{x \to −4^+}f(x)\);\(\displaystyle \lim_{x→−4}f(x);\;f(−4)\)
\(\displaystyle \lim_{x \to −2^−}f(x\));\(\displaystyle \lim_{x \to −2^+}f(x)\);\(\displaystyle \lim_{x→−2}f(x);\;f(−2)\)
\( \displaystyle \lim_{x \to 1^−}f(x)\);\(\displaystyle \lim_{x \to 1^+}f(x)\);\(\displaystyle \lim_{x \to 1}f(x);\;f(1)\)
\( \displaystyle \lim_{x \to 3^−}f(x)\);\(\displaystyle \lim_{x \to 3^+}f(x)\);\(\displaystyle \lim_{x \to 3}f(x);\;f(3)\)

Grafu ya kazi f (x) iliyoelezwa na mipaka na maadili hapo juu. Kuna curve laini kwa maadili chini ya x=-2; katika (-2, 3), kuna mduara wazi. Kuna curve laini kati ya (-2, 1] na mduara imefungwa katika (1,6). Kuna mduara wazi katika (1,3), na curve laini kuenea kutoka huko chini asymptotically kwa infinity hasi pamoja x=3. Kazi pia inazunguka kwa urahisi pamoja x=3 upande mwingine, pia ikitambulisha kwa infinity hasi. Kazi hiyo inabadilisha concavity katika roboduara ya kwanza karibu y = 4.5 na inaendelea. — Kielelezo\(\PageIndex{10}\): Grafu inaonyesha\(f(x)\).

Suluhisho

Kutumia ufafanuzi hapo juu na grafu ya kumbukumbu, tunawasili maadili yafuatayo:

\(\displaystyle \lim_{x \to −4^−}f(x)=0\);\(\displaystyle \lim_{x \to −4^+}f(x)=0\);\(\displaystyle \lim_{x \to −4}f(x)=0;\;f(−4)=0\)
\(\displaystyle \lim_{x \to −2^−}f(x)=3\)\(\displaystyle \lim_{x \to −2^+}f(x)=3\);\(\displaystyle \lim_{x \to −2}f(x)=3;\;f(−2)\) haijulikani
\(\displaystyle \lim_{x \to 1^−}f(x)=6\);\(\displaystyle \lim_{x \to 1^+}f(x)=3\);\(\displaystyle \lim_{x \to 1}f(x)\) DNE;\(f(1)=6\)
\(\displaystyle \lim_{x \to 3^−}f(x)=−∞\);\(\displaystyle \lim_{x \to 3^+}f(x)=−∞\)\(\displaystyle \lim_{x \to 3}f(x)=−∞\);\(f(3)\) haijulikani

Zoezi\(\PageIndex{7}\)

Tathmini\(\displaystyle\lim_{x \to 1}f(x)\) kwa\(f(x)\) inavyoonekana hapa:

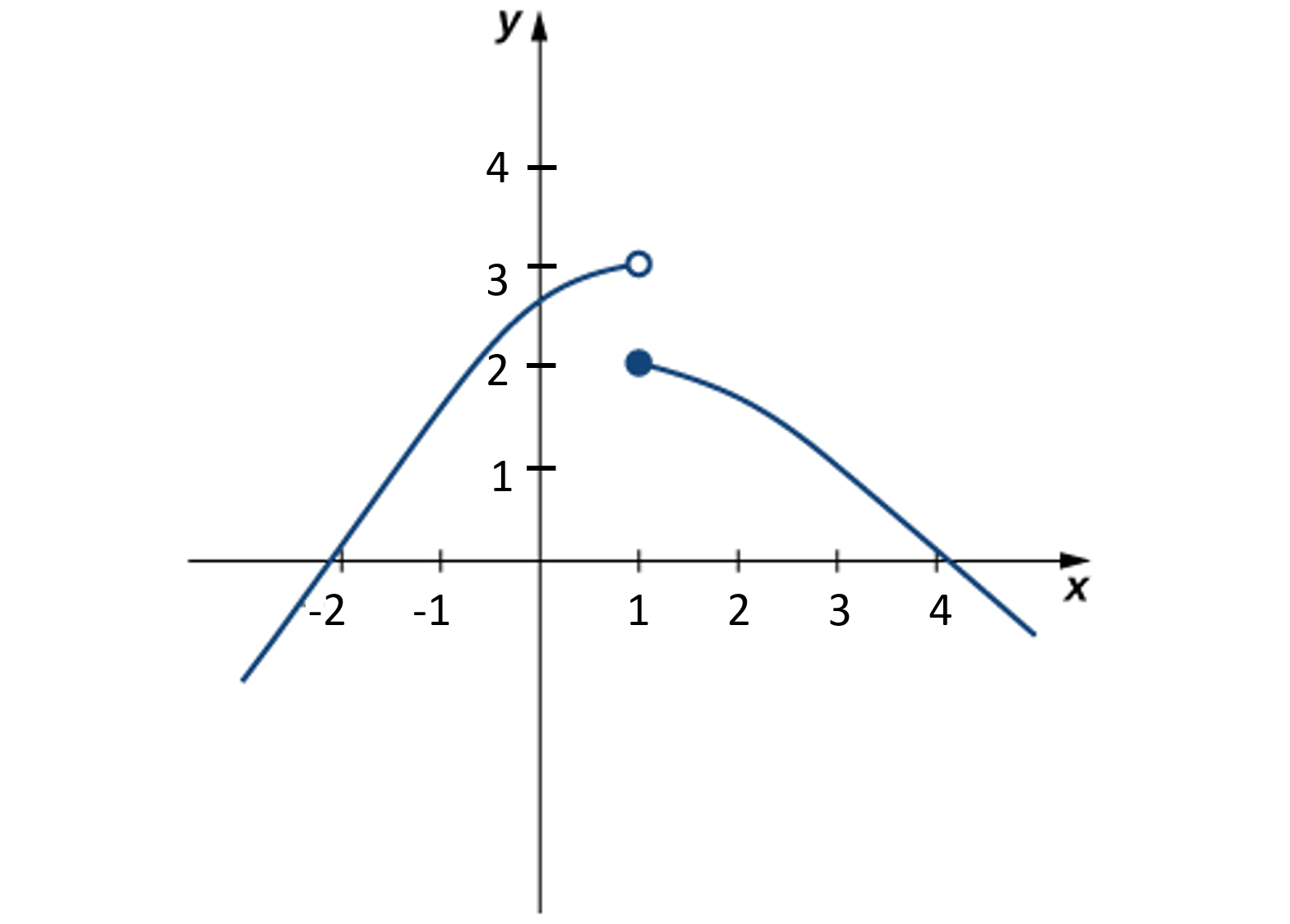
Grafu ya kazi ya kipande. Sehemu ya kwanza inakuja kutoka kwa quadrant ya tatu hadi ya kwanza, ikivuka kupitia quadrant ya pili. Ambapo mwisho itakuwa katika roboduara ya kwanza ni mduara wazi. Sehemu ya pili inaanza kwenye mduara uliofungwa vitengo vichache chini ya mduara wazi. Ni curves chini kutoka roboduara moja kwa roboduara nne. — Kielelezo\(\PageIndex{11}\). Grafu ya kazi ya kipande\(f\).

Kidokezo: Linganisha kikomo kutoka kulia na kikomo kutoka upande wa kushoto.
Jibu: \(\displaystyle\lim_{x \to 1}f(x)\)haipo

Mfano\(\PageIndex{8}\): Einstein’s Equation

Katika Sura kopo sisi zilizotajwa kwa ufupi jinsi Albert Einstein ilionyesha kuwa kikomo ipo kwa jinsi ya kufunga kitu chochote unaweza kusafiri. Kutokana equation Einstein kwa wingi wa kitu kusonga

\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]

ni thamani gani ya hii amefungwa?

picha ya spaceship futuristic kasi kwa njia ya nafasi ya kina. — Kielelezo\(\PageIndex{12}\). (Mikopo: NASA)

Suluhisho

Hatua yetu ya mwanzo ni equation Einstein kwa wingi wa kitu kusonga,

\[m=\dfrac{m_0}{\sqrt{1−\frac{v^2}{c^2}}}, \nonumber \]

\(m_0\)wapi wingi wa kitu katika mapumziko,\(v\) ni kasi yake, na\(c\) ni kasi ya mwanga. Ili kuona jinsi wingi unavyobadilika kwa kasi ya juu, tunaweza kupiga uwiano wa raia\(m/m_0\) kama kazi ya uwiano wa kasi,\(v/c\) (Kielelezo\(\PageIndex{13}\)).

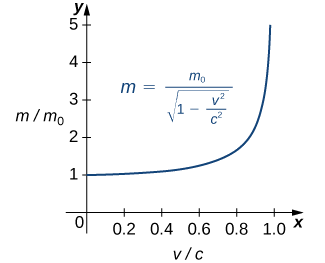
Grafu inayoonyesha uwiano wa raia kama kazi ya uwiano wa kasi katika equation ya Einstein kwa wingi wa kitu cha kusonga. Mhimili x ni uwiano wa kasi, v/c. mhimili y ni uwiano wa raia, m/m0. Ulinganisho wa kazi ni m = m0/sqrt (1 - v2/c2). Grafu ni tu katika quadrant 1. Inaanza saa (0,1) na hupunguza kwa upole hadi karibu 0.8, ambapo huongeza inaonekana kwa kiasi kikubwa; kuna asymptote ya wima kwenye v/c (au x) = 1. — Kielelezo\(\PageIndex{13}\): Grafu hii inaonyesha uwiano wa raia kama kazi ya uwiano wa kasi katika equation ya Einstein kwa wingi wa kitu cha kusonga.

Tunaweza kuona kwamba kama uwiano wa kasi unakaribia 1—yaani, kama kasi ya kitu inakaribia kasi ya mwanga-uwiano wa raia huongezeka bila kufungwa. Kwa maneno mengine, kazi ina asymptote wima katika\(v/c=1\). Tunaweza kujaribu maadili machache ya uwiano huu ili kupima wazo hili.

Jedwali\(\PageIndex{8}\)
\(v/c\)	\(\sqrt{1-\frac{v^2}{c^2}}\)	\(m/m_o\)
\ (v/c\)” style="text-align:katikati; "> 0.99	\ (\ sqrt {1-\ frac {v^2} {c ^ 2}}\)” style="Nakala-align:katikati; "> 0.1411	\ (m/m_o\)” style="Nakala-align:katikati; "> 7.089
\ (v/c\)” style="Nakala-align:katikati; "> 0.999	\ (\ sqrt {1-\ frac {v^2} {c ^ 2}}\)” style="text-align:katikati; "> 0.0447	\ (m/m_o\)” style="Nakala-align:katikati; "> 22.37
\ (v/c\)” style="Nakala-align:katikati; "> 0.9999	\ (\ sqrt {1-\ frac {v^2} {c ^ 2}}\)” style="Nakala-align:katikati; "> 0.0141	\ (m/m_o\)” style="Nakala-align:center; "> 70.7

Kwa hiyo, kulingana na Jedwali\(\PageIndex{8}\):, ikiwa kitu kilicho na uzito wa kilo 100 kinaenda saa 0.9999c, uzito wake unakuwa kilo 7071. Kwa kuwa hakuna kitu kinachoweza kuwa na wingi usio na kipimo, tunahitimisha kuwa hakuna kitu kinachoweza kusafiri au zaidi ya kasi ya mwanga.

Dhana muhimu

Jedwali la maadili au grafu inaweza kutumika kukadiria kikomo.
Kama kikomo cha kazi katika hatua haipo, bado inawezekana kwamba mipaka kutoka kushoto na kulia katika hatua hiyo inaweza kuwepo.
Ikiwa mipaka ya kazi kutoka upande wa kushoto na kulia iko na ni sawa, basi kikomo cha kazi ni thamani ya kawaida.
Tunaweza kutumia mipaka kuelezea tabia usio wa kazi katika hatua.

Mlinganyo muhimu

Ufafanuzi wa Intuitive wa Kikomo

\(\displaystyle \lim_{x \to a}f(x)=L\)

Mipaka miwili muhimu

\(\displaystyle \lim_{x \to a}x=a \qquad \lim_{x \to a}c=c\)

Mipaka ya upande mmoja

\(\displaystyle \lim_{x \to a^−}f(x)=L \qquad \lim_{x \to a^+}f(x)=L\)

Mipaka isiyo na mwisho kutoka kushoto

\(\displaystyle \lim_{x \to a^−}f(x)=+∞ \qquad \lim_{x \to a^−} f(x)=−∞\)

Mipaka usio na mwisho kutoka kulia

\(\displaystyle \lim_{x \to a^+}f(x)=+∞ \qquad \lim_{x \to a^+} f(x)=−∞\)

Mipaka miwili isiyo na mwisho

\(\displaystyle \lim_{x \to a}f(x)=+∞\):\(\displaystyle \lim_{x \to a^−}f(x)=+∞\) na\(\displaystyle \lim_{x \to a^+} f(x)=+∞\)

\(\displaystyle \lim_{x \to a}f(x)=−∞\):\(\displaystyle \lim_{x \to a^−}f(x)=−∞\) na\(\displaystyle \lim_{x \to a^+} f(x)=−∞\)

faharasa

kikomo usio: kazi ina kikomo usio katika hatua\(a\) kama ama kuongezeka au itapungua bila amefungwa kama inakaribia\(a\)

ufafanuzi wa intuitive wa kikomo: Ikiwa maadili yote ya kazi\(f(x)\) yanakaribia nambari halisi\(L\) kama maadili ya\(x(≠a)\) mbinu a,\(f(x)\) inakaribia L

kikomo cha upande mmoja: Kikomo upande mmoja wa kazi ni kikomo kuchukuliwa kutoka ama kushoto au kulia

asymptote ya wima: Kazi ina asymptote wima katika\(x=a\) kama kikomo kama\(x\) mbinu\(a\) kutoka kulia au kushoto ni usio