1.4: Kazi za Inverse

Malengo ya kujifunza

• Kuamua hali ya wakati kazi ina inverse.
• Tumia mtihani wa mstari wa usawa kutambua wakati kazi ni moja kwa moja.
• Kupata inverse ya kazi fulani.
• Chora grafu ya kazi ya inverse.
• Tathmini kazi za trigonometric inverse.

Kazi ya inverse inarudia operesheni iliyofanywa na kazi fulani. Kwa maneno mengine, chochote kazi gani, kazi inverse huiondoa. Katika sehemu hii, sisi kufafanua kazi inverse rasmi na kusema hali muhimu kwa ajili ya kazi inverse kuwepo. Tunachunguza jinsi ya kupata kazi inverse na kujifunza uhusiano kati ya grafu ya kazi na grafu ya inverse yake. Kisha tunatumia mawazo haya kufafanua na kujadili mali ya kazi za trigonometric inverse.

Kuwepo kwa Kazi ya Inverse

Tunaanza kwa mfano. Kutokana na kazi$f$ na pato$y=f(x)$, sisi mara nyingi nia ya kutafuta nini thamani au maadili$x$ walikuwa mapped$y$ na$f$. Kwa mfano, fikiria kazi$f(x)=x^3+4$. Tangu pato$y=x^3+4$ lolote, tunaweza kutatua equation hii$x$ kwa kupata kwamba pembejeo ni$x=\sqrt[3]{y−4}$. equation Hii amefafanua$x$ kama kazi ya$y$. Denoting kazi hii kama$f^{−1}$$x=f^{−1}(y)=\sqrt[3]{y−4}$, na kuandika, tunaona kwamba kwa yeyote$x$ katika uwanja wa$f,f^{−1}$$f(x))=f^{−1}(x^3+4)=x$. Hivyo, kazi hii mpya$f^{−1}$, “undid” nini kazi ya awali$f$ alifanya. Kazi na mali hii inaitwa kazi ya inverse ya kazi ya awali.

Ufafanuzi: Kazi za Inverse

Kutokana$f$ na kazi na kikoa$D$ na upeo$R$, kazi yake ya inverse (ikiwa ipo) ni kazi$f^{−1}$ na kikoa$R$ na aina$D$ kama hiyo$f^{−1}(y)=x$ ikiwa na tu ikiwa$f(x)=y$. Kwa maneno mengine, kwa ajili ya kazi$f$ na inverse yake$f^{−1}$,

$$f^{−1}(f(x))=x \nonumber$$

kwa ajili ya wote$x$ katika$D$ na

$$f(f^{−1}(y))=y \nonumber$$

kwa ajili ya wote$y$ katika$R$.

Kumbuka kwamba$f^{−1}$ ni kusoma kama “$f$inverse.” Hapa,$−1$ si kutumika kama exponent hivyo

$$f^{−1}(x)≠ \dfrac{1}{f(x)}. \nonumber$$

Kielelezo$\PageIndex{1}$ inaonyesha uhusiano kati ya uwanja na mbalimbali ya$f$ na uwanja na mbalimbali ya$f^{−1}$.

Kielelezo$\PageIndex{1}$: Kutokana$f$ na kazi na inverse yake$f^{−1},f^{−1}(y)=x$ kama na tu kama$f(x)=y$. Mbalimbali ya$f$ inakuwa uwanja wa$f^{−1}$ na uwanja wa$f$ inakuwa mbalimbali ya$f^{−1}$.

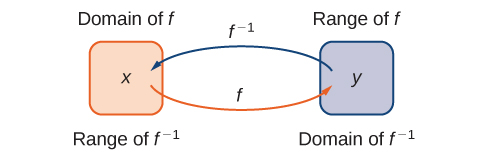
Kumbuka kwamba kazi ina pato moja hasa kwa kila pembejeo. Kwa hiyo, kufafanua kazi inverse, tunahitaji ramani kila pembejeo kwa pato moja hasa. Kwa mfano, hebu jaribu kupata kazi inverse kwa$f(x)=x^2$. Kutatua equation$y=x^2$ kwa$x$, sisi kufika katika equation$x=±\sqrt{y}$. Equation hii haina kuelezea$x$ kama kazi ya$y$ kwa sababu kuna ufumbuzi mbili kwa equation hii kwa kila$y>0$. Tatizo na kujaribu kupata kazi inverse kwa$f(x)=x^2$ ni kwamba pembejeo mbili zinatumwa kwa pato sawa kwa kila pato$y>0$. Kazi$f(x)=x^3+4$ iliyojadiliwa mapema haikuwa na tatizo hili. Kwa kazi hiyo, kila pembejeo ilitumwa kwa pato tofauti. Kazi inayotuma kila pembejeo kwa pato tofauti inaitwa kazi moja kwa moja.

Ufafanuzi: Kazi moja kwa moja

Tunasema kazi$f$ ni moja kwa moja kazi kama$f(x_1)≠f(x_2)$ wakati$x_1≠x_2$.

Njia moja ya kuamua kama kazi ni moja kwa moja ni kwa kuangalia grafu yake. Ikiwa kazi ni moja kwa moja, basi hakuna pembejeo mbili zinaweza kutumwa kwa pato sawa. Kwa hiyo, ikiwa tunapata mstari usio na usawa popote kwenye$xy$ ndege ya ndege, kulingana na mtihani wa mstari usio na usawa, hauwezi kuingilia grafu zaidi ya mara moja. Tunaona kwamba mtihani wa mstari wa usawa ni tofauti na mtihani wa mstari wa wima. Mtihani wa mstari wa wima huamua kama grafu ni grafu ya kazi. Mtihani wa mstari wa usawa huamua kama kazi ni moja kwa moja (Kielelezo$\PageIndex{2}$).

Mtihani wa mstari wa usawa

Kazi$f$ ni moja kwa moja ikiwa na tu ikiwa kila mstari wa usawa unaingilia grafu ya$f$ si zaidi ya mara moja.

Kielelezo$\PageIndex{2}$: (a) kazi$f(x)=x^2$ si moja kwa moja kwa sababu inashindwa usawa line mtihani. (b) Kazi$f(x)=x^3$ ni moja kwa moja kwa sababu inapita mtihani wa mstari wa usawa.

Mfano$\PageIndex{1}$: Determining Whether a Function Is One-to-One

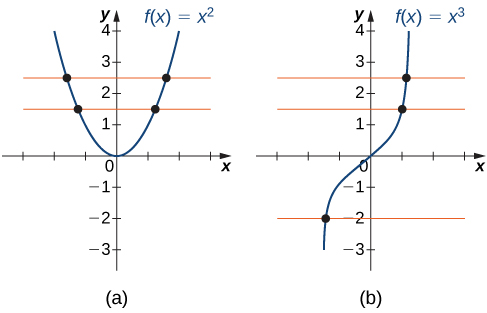
Kwa kila moja ya kazi zifuatazo, tumia mtihani wa mstari wa usawa ili uone ikiwa ni moja kwa moja.

a)

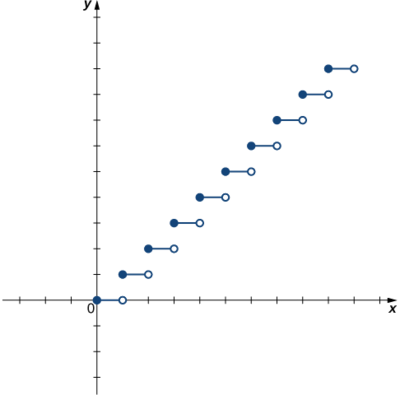
b)

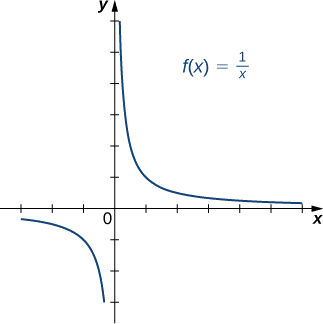
Suluhisho

a) Kwa kuwa mstari$y=n$ wa usawa wa integer yoyote$n≥0$ huingilia grafu zaidi ya mara moja, kazi hii sio moja kwa moja.

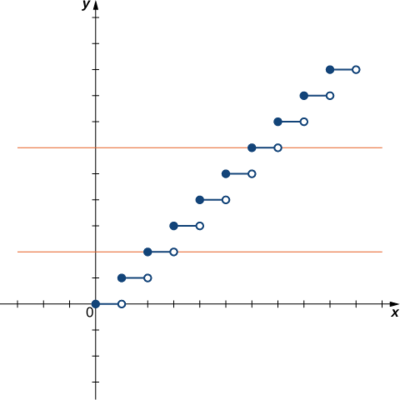
b) Kwa kuwa kila mstari wa usawa unaingilia grafu mara moja (zaidi), kazi hii ni moja kwa moja.

Zoezi$\PageIndex{1}$

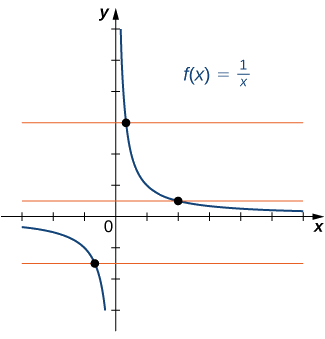
Je! Kazi$f$ imefunikwa katika picha inayofuata moja kwa moja?

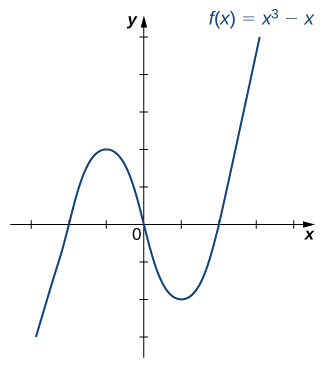
Suluhisho

Tumia mtihani wa mstari usio na usawa.

Jibu

Hapana

Kutafuta Inverse ya Kazi

Sasa tunaweza kufikiria kazi moja kwa moja na kuonyesha jinsi ya kupata inverses yao. Kumbuka kwamba kazi ramani mambo katika uwanja wa$f$ vipengele katika aina mbalimbali ya$f$. kazi inverse ramani kila kipengele kutoka mbalimbali ya$f$ nyuma kwa kipengele yake sambamba kutoka uwanja wa$f$. Kwa hiyo, ili kupata kazi inverse ya kazi moja kwa moja$f$, kutokana na yoyote$y$ katika aina mbalimbali$f$, tunahitaji kuamua ambayo$x$ katika uwanja wa$f$ satisfies$f(x)=y$. Kwa kuwa$f$ ni moja kwa moja, kuna thamani moja sawa$x$. Tunaweza kupata kwamba thamani$x$ kwa kutatua equation$f(x)=y$ kwa$x$. Kufanya hivyo, tuna uwezo wa kuandika$x$ kama kazi ya$y$ ambapo uwanja wa kazi hii ni aina mbalimbali$f$ na aina mbalimbali ya kazi hii mpya ni uwanja wa$f$. Kwa hiyo, kazi hii ni inverse ya$f$, na tunaandika$x=f^{−1}(y)$. Kwa kuwa sisi kawaida kutumia variable$x$ kuashiria variable huru na y kuashiria variable tegemezi, sisi mara nyingi interchange majukumu ya$x$ na$y$, na kuandika$y=f^{−1}(x)$. Anayewakilisha kazi inverse kwa njia hii pia ni muhimu baadaye wakati sisi graph kazi$f$ na inverse yake$f^{−1}$ juu ya shoka sawa.

Mkakati wa Kutatua Matatizo: Kutafuta Kazi ya Inverse

1. Kutatua equation$y=f(x)$ kwa$x$.
2. Kubadilishana vigezo$x$$y$ na kuandika$y=f^{−1}(x)$.

Mfano$\PageIndex{2}$: Finding an Inverse Function

Pata inverse kwa kazi$f(x)=3x−4.$ Hali ya kikoa na upeo wa kazi ya inverse. Thibitisha kwamba$f^{−1}(f(x))=x.$

Suluhisho

Fuata hatua ilivyoainishwa katika mkakati.

Hatua ya 1. Ikiwa$y=3x−4,$ basi$3x=y+4$ na$x=\frac{1}{3}y+\frac{4}{3}.$

Hatua ya 2. Andika upya kama$y=\frac{1}{3}x+\frac{4}{3}$ na waache$y=f^{−1}(x)$ .Kwa hiyo,$f^{−1}(x)=\frac{1}{3}x+\frac{4}{3}$.

Tangu uwanja wa$f$ ni$(−∞,∞)$, mbalimbali ya$f^{−1}$ ni$(−∞,∞)$. Kwa kuwa mbalimbali ya$f$ ni$(−∞,∞)$, uwanja wa$f^{−1}$ ni$(−∞,∞)$.

Unaweza kuthibitisha kwamba$f^{−1}(f(x))=x$ kwa kuandika

$f^{−1}(f(x))=f^{−1}(3x−4)=\frac{1}{3}(3x−4)+\frac{4}{3}=x−\frac{4}{3}+\frac{4}{3}=x.$

Kumbuka kwamba$f^{−1}(x)$ kwa kuwa inverse ya$f(x)$, wote$f^{−1}(f(x))=x$ na$f(f^{−1}(x))=x$ kwa wote$x$ katika uwanja wa kazi ndani.

Zoezi$\PageIndex{2}$

Pata inverse ya kazi$f(x)=3x/(x−2)$. Weka kikoa na upeo wa kazi ya inverse.

Kidokezo

Tumia Mkakati wa Kutatua Matatizo kwa kutafuta kazi za kinyume.

Jibu

$f^{−1}(x)=\dfrac{2x}{x−3}$. uwanja wa$f^{−1}$ ni$\{x\,|\,x≠3\}$. mbalimbali ya$f^{−1}$ ni$\{y\,|\,y≠2\}$.

Graphing Inverse Kazi

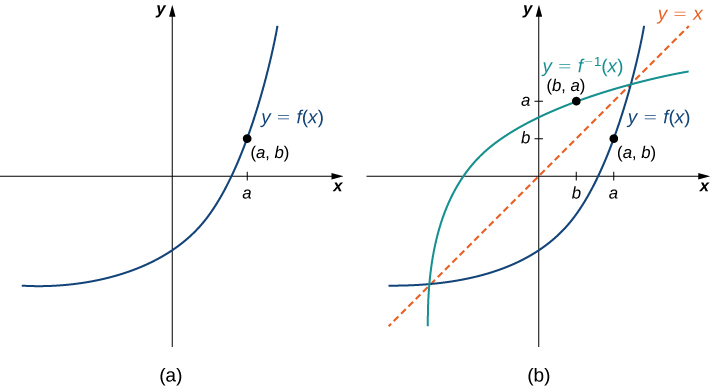
Hebu fikiria uhusiano kati ya grafu ya kazi$f$ na grafu ya inverse yake. Fikiria grafu ya$f$ inavyoonekana katika Kielelezo$\PageIndex{3}$ na uhakika$(a,b)$ kwenye grafu. Tangu$b=f(a)$, basi$f^{−1}(b)=a$. Kwa hiyo, wakati sisi grafu$f^{−1}$, uhakika$(b,a)$ ni kwenye grafu. Matokeo yake, grafu ya$f^{−1}$ ni mfano wa grafu ya$f$ juu ya mstari$y=x$.

Kielelezo$\PageIndex{3}$: (a) graph ya kazi hii$f$ inaonyesha uhakika$(a,b)$ juu ya grafu ya$f$. (b) Kwa kuwa$(a,b)$ ni juu ya grafu ya$f$, uhakika$(b,a)$ ni juu ya grafu ya$f^{−1}$. Grafu ya$f^{−1}$ ni mfano wa grafu ya$f$ juu ya mstari$y=x$.

Mfano$\PageIndex{3}$: Sketching Graphs of Inverse Functions

Kwa grafu ya$f$ katika picha ifuatayo, mchoro grafu ya$f^{−1}$ kwa sketching mstari$y=x$ na kutumia ulinganifu. Kutambua uwanja na aina mbalimbali ya$f^{−1}$.

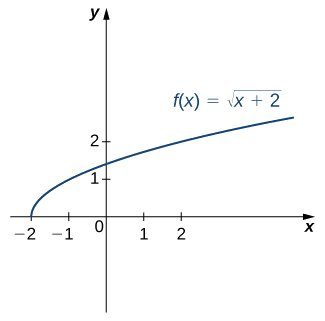
Suluhisho

Fikiria grafu kuhusu mstari$y=x$. uwanja wa$f^{−1}$ ni$[0,∞)$. mbalimbali ya$f^{−1}$ ni$[−2,∞)$. Kwa kutumia mkakati uliopita kwa ajili ya kutafuta kazi inverse, tunaweza kuthibitisha kwamba kazi inverse ni$f^{−1}(x)=x^2−2$, kama inavyoonekana katika grafu.

Zoezi$\PageIndex{3}$

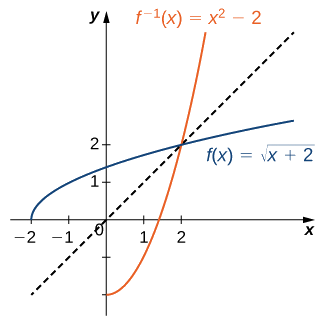
Mchoro grafu ya$f(x)=2x+3$ na grafu ya inverse yake kwa kutumia mali ya ulinganifu wa kazi za inverse.

Kidokezo

Grafu ni symmetric kuhusu mstari$y=x$

Jibu

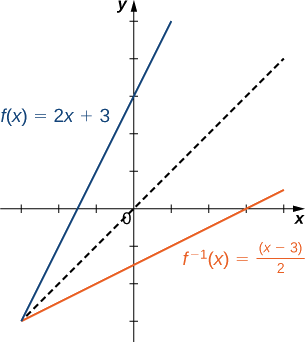
Kuzuia Domains

Kama tulivyoona,$f(x)=x^2$ hana kazi inverse kwa sababu si moja kwa moja. Hata hivyo, tunaweza kuchagua subset ya uwanja wa$f$ vile kwamba kazi ni moja kwa moja. Subset hii inaitwa kikoa kilichozuiliwa. Kwa kuzuia uwanja wa$f$, tunaweza kufafanua kazi mpya$g$ kama kwamba uwanja wa$g$ ni kikoa vikwazo ya$f$ na$g(x)=f(x)$ kwa wote$x$ katika uwanja wa$g$. Basi tunaweza kufafanua kazi inverse kwa ajili ya$g$ juu ya uwanja huo. Kwa mfano, tangu$f(x)=x^2$ ni moja kwa moja juu ya muda$[0,∞)$, tunaweza kufafanua kazi mpya$g$ kama kwamba uwanja wa$g$ ni$[0,∞)$ na$g(x)=x^2$ kwa wote$x$ katika uwanja wake. Kwa kuwa$g$ ni kazi moja kwa moja, ina kazi inverse, iliyotolewa na formula$g^{−1}(x)=\sqrt{x}$. Kwa upande mwingine, kazi pia$f(x)=x^2$ ni moja kwa moja kwenye uwanja$(−∞,0]$. Kwa hiyo, tunaweza pia kufafanua kazi mpya$h$ kama kwamba uwanja wa$h$ ni$(−∞,0]$ na$h(x)=x^2$ kwa wote$x$ katika uwanja wa$h$. Kisha$h$ ni kazi moja kwa moja na lazima pia kuwa na inverse. Inverse yake hutolewa na formula$h^{−1}(x)=−\sqrt{x}$ (Kielelezo$\PageIndex{4}$).

Kielelezo$\PageIndex{4}$: (a) Kwa$g(x)=x^2$ vikwazo$[0,∞)$,$g^{−1}(x)=\sqrt{x}$. (b) Kwa$h(x)=x^2$ vikwazo$(−∞,0]$,$h^{−1}(x)=−\sqrt{x}$.

Mfano$\PageIndex{4}$: Restricting the Domain

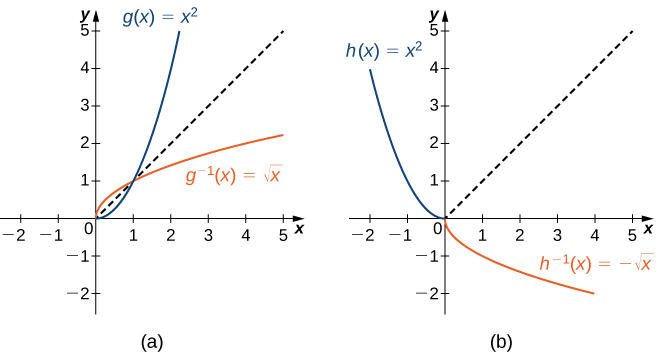
Fikiria kazi$f(x)=(x+1)^2$.

1. Mchoro grafu ya$f$ na kutumia usawa line mtihani kuonyesha kwamba$f$ si moja kwa moja.
2. Onyesha kwamba$f$ ni moja kwa moja kwenye kikoa kilichozuiliwa$[−1,∞)$. Tambua kikoa na upeo kwa inverse ya$f$ kwenye kikoa hiki kilichozuiliwa na upate fomu ya$f^{−1}$.

Suluhisho

a) Grafu ya$f$ ni grafu ya$1$ kitengo cha kushoto$y=x^2$ kilichobadilishwa. Kwa kuwa kuna mstari usio na usawa unaoingilia grafu zaidi ya mara moja,$f$ sio moja kwa moja.

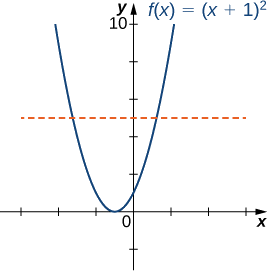
b) Wakati huo$[−1,∞),\;f$ ni moja kwa moja.

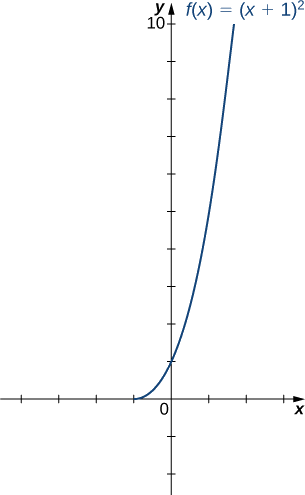
Domain na mbalimbali ya$f^{−1}$ hutolewa na mbalimbali na uwanja wa$f$, kwa mtiririko huo. Kwa hiyo, uwanja wa$f^{−1}$ ni$[0,∞)$ na aina mbalimbali$f^{−1}$ ni$[−1,∞)$. Ili kupata formula kwa$f^{−1}$, kutatua equation$y=(x+1)^2$ kwa$x.$ Kama$y=(x+1)^2$, basi$x=−1±\sqrt{y}$. Kwa kuwa sisi ni kuzuia uwanja kwa muda ambapo$x≥−1$, tunahitaji$±\sqrt{y}≥0$. Kwa hiyo,$x=−1+\sqrt{y}$. $x$Kubadilishana na$y$, tunaandika$y=−1+\sqrt{x}$ na kuhitimisha hilo$f^{−1}(x)=−1+\sqrt{x}$.

Zoezi$\PageIndex{4}$

Fikiria$f(x)=1/x^2$ vikwazo kwenye kikoa$(−∞,0)$. Thibitisha kwamba$f$ ni moja kwa moja kwenye uwanja huu. Kuamua uwanja na mbalimbali ya inverse ya$f$ na kupata formula kwa$f^{−1}$.

Kidokezo

Domain na mbalimbali ya$f^{−1}$ hutolewa na mbalimbali na uwanja wa$f$, kwa mtiririko huo. Ili kupata$f^{−1}$, tatua$y=1/x^2$$x$.

Jibu

uwanja wa$f^{−1}$ ni$(0,∞)$. mbalimbali ya$f^{−1}$ ni$(−∞,0)$. Kazi ya inverse inapewa na formula$f^{−1}(x)=−1/\sqrt{x}$.

Kazi za Trigonometric Inverse

Kazi sita za msingi za trigonometric ni mara kwa mara, na kwa hiyo sio moja kwa moja. Hata hivyo, ikiwa tunazuia uwanja wa kazi ya trigonometric kwa muda ambapo ni moja kwa moja, tunaweza kufafanua inverse yake. Fikiria kazi ya sine. kazi sine ni moja kwa moja juu ya idadi usio wa vipindi, lakini mkataba kiwango ni kuzuia uwanja kwa muda$\left[−\frac{π}{2},\frac{π}{2}\right]$. Kwa kufanya hivyo, sisi kufafanua inverse sine kazi kwenye uwanja$[−1,1]$ kama kwamba kwa yeyote$x$ katika muda$[−1,1]$, inverse sine kazi inatuambia ambayo angle$θ$ katika muda$\left[−\frac{π}{2},\frac{π}{2}\right]$ satisfies$\sin θ=x$. Vile vile, tunaweza kuzuia nyanja za kazi nyingine za trigonometric ili kufafanua kazi za trigonometric inverse, ambazo ni kazi ambazo zinatuambia angle katika kipindi fulani ina thamani maalum ya trigonometric.

Ufafanuzi: inverse trigonometric kazi

Kazi ya sine inverse, iliyoashiria$\sin^{−1}$ au$\arcsin$, na kazi ya cosine inverse, iliyoashiria$\cos^{−1}$ au$\arccos$, inaelezwa kwenye uwanja$D=\{x|−1≤x≤1\}$ kama ifuatavyo:

$\sin^{−1}(x)=y$

• ikiwa na tu ikiwa$\sin(y)=x$ na$−\frac{π}{2}≤y≤\frac{π}{2}$;

$\cos^{−1}(x)=y$

• kama na tu kama$\cos(y)=x$ na$0≤y≤π$.

Kazi ya tangent inverse, iliyoashiria$\tan^{−1}$ au$\arctan$, na kazi ya cotangent inverse, iliyoashiria$\cot^{−1}$ au$\operatorname{arccot}$, inaelezwa kwenye uwanja$D=\{x|−∞<x<∞\}$ kama ifuatavyo:

$\tan^{−1}(x)=y$

• ikiwa na tu ikiwa$\tan(y)=x$ na$−\frac{π}{2}<y<\frac{π}{2}$;

$\cot^{−1}(x)=y$

• kama na tu kama$\cot(y)=x$ na$0<y<π$.

Kazi ya cosecant inverse, iliyoashiria$\csc^{−1}$ au$\operatorname{arccsc}$, na kazi ya secant inverse, iliyoashiria$\sec^{−1}$ au$\operatorname{arcsec}$, inaelezwa kwenye uwanja$D=\{x\,|\,|x|≥1\}$ kama ifuatavyo:

$\csc^{−1}(x)=y$

• ikiwa na tu ikiwa$\csc(y)=x$ na$−\frac{π}{2}≤y≤\frac{π}{2}, \, y≠0$;

$\sec^{−1}(x)=y$

• kama na tu kama$\sec(y)=x$ na$0≤y≤π, \, y≠π/2$.

Ili kuchora kazi za trigonometric inverse, tunatumia grafu za kazi za trigonometric zilizozuiliwa kwenye nyanja zilizoelezwa mapema na kutafakari grafu kuhusu mstari$y=x$ (Kielelezo$\PageIndex{5}$).

Kielelezo$\PageIndex{5}$: Grafu ya kila kazi za trigonometric inverse ni kutafakari juu ya mstari$y=x$ wa kazi inayozuia trigonometric inayofanana.

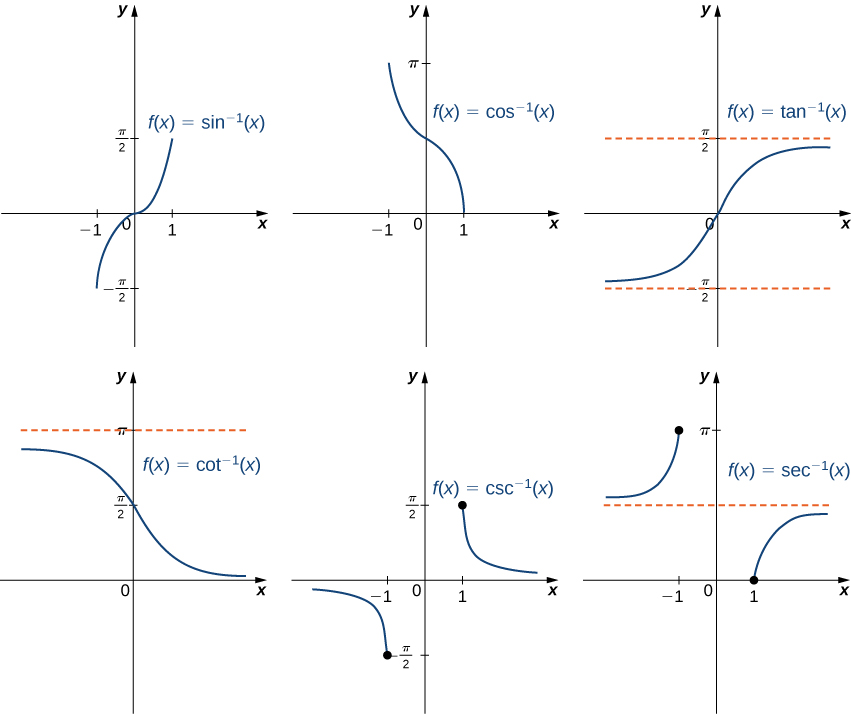
Wakati wa kutathmini kazi ya trigonometric inverse, pato ni angle. Kwa mfano, kutathmini$\cos^{−1}\left(\frac{1}{2}\right)$, tunahitaji kupata angle$θ$ kama hiyo$\cos θ=\frac{1}{2}$. Kwa wazi, pembe nyingi zina mali hii. Hata hivyo, kutokana na ufafanuzi wa$\cos^{−1}$, tunahitaji angle$θ$ ambayo sio tu kutatua equation hii, lakini pia iko katika muda$[0,π]$. Tunahitimisha kuwa$\cos^{−1}\left(\frac{1}{2}\right)=\frac{π}{3}$.

Sasa tunazingatia muundo wa kazi ya trigonometric na inverse yake. Kwa mfano, fikiria maneno mawili$\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)$ na$\sin^{−1}(\sin(π)).$

Kwa kwanza, sisi kurahisisha kama ifuatavyo:

$$\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)=\sin\left(\frac{π}{4}\right)=\frac{\sqrt{2}}{2}.\nonumber$$

Kwa pili, tuna

$$\sin^{−1}(\sin(π))=\sin^{−1}(0)=0.\nonumber$$

Kazi inverse inatakiwa “kurekebisha” kazi ya awali, kwa nini si Kumbuka$\sin^{−1}(\sin(π))=π?$ ufafanuzi wetu wa kazi inverse, kazi$f$ na inverse yake$f^{−1}$ kukidhi masharti$f(f^{−1}(y))=y$ kwa wote$y$ katika uwanja wa$f^{−1}$ na$f^{−1}(f(x))=x$ kwa wote$x$ uwanja wa$f$, hivyo nini kilichotokea hapa? Suala ni kwamba inverse sine kazi$\sin^{−1}$,, ni kinyume cha vikwazo sine kazi defined kwenye uwanja$\left[−\frac{π}{2},\frac{π}{2}\right]$. Kwa hiyo,$x$ kwa wakati huo$[−\frac{π}{2},\frac{π}{2}]$, ni kweli kwamba$\sin^{−1}(\sin x)=x$. Hata hivyo, kwa maadili ya$x$ nje ya muda huu, equation haina kushikilia, ingawa$\sin^{−1}(\sin x)$ inaelezwa kwa namba zote halisi$x$.

Nini kuhusu$\sin(\sin^{−1}y)?$ Je, hiyo ina suala sawa? Jibu ni hapana. Kwa kuwa uwanja wa$\sin^{−1}$ ni muda$[−1,1]$, sisi kuhitimisha kwamba$\sin\left(\sin^{−1}y\right)=y$ kama$−1≤y≤1$ na kujieleza si defined kwa maadili mengine ya$y$. Kwa muhtasari,

$\sin(\sin^{−1}y)=y$kama$−1≤y≤1$

na

$\sin^{−1}(\sin x)=x$kama$−\frac{π}{2}≤x≤\frac{π}{2}.$

Vile vile, kwa kazi ya cosine,

$\cos(\cos^{−1}y)=y$kama$−1≤y≤1$

na

$\cos^{−1}(\cos x)=x$kama$0≤x≤π.$

Mali kama hiyo inashikilia trigonometric nyingine ya kazi na inverses yao.

Mfano$\PageIndex{5}$: Evaluating Expressions Involving Inverse Trigonometric Functions

Tathmini kila moja ya maneno yafuatayo.

1. $\sin^{−1}\left(−\frac{\sqrt{3}}{2}\right)$
2. $\tan\left(\tan^{−1}\left(−\frac{1}{\sqrt{3}}\right)\right)$
3. $\cos^{−1}\left(\cos\left(\frac{5π}{4}\right)\right)$
4. $\sin^{−1}\left(\cos\left(\frac{2π}{3}\right)\right)$

Suluhisho

1. Kutathmini$\sin^{−1}(−\sqrt{3}/2)$ ni sawa na kutafuta angle$θ$ kama hiyo$\sin θ=−\sqrt{3}/2$ na$−π/2≤θ≤π/2$. Pembe$θ=−π/3$ hutimiza hali hizi mbili. Kwa hiyo,$\sin^{−1}(−\sqrt{3}/2)=−π/3$.
2. Kwanza tunatumia ukweli kwamba$\tan^{−1}(−1/\sqrt{3})=−π/6.$ Kisha$\tan(-π/6)=−1/\sqrt{3}$. Kwa hiyo,$\tan(\tan^{−1}(−1/\sqrt{3}))=−1/\sqrt{3}$.
3. Kutathmini$\cos^{−1}(\cos(5π/4))$, kwanza utumie ukweli kwamba$\cos(5π/4)=−\sqrt{2}/2$. Kisha tunahitaji kupata angle$θ$ kama hiyo$\cos(θ)=−\sqrt{2}/2$ na$0≤θ≤π$. Tangu$3π/4$ satisfies hali hizi zote mbili, tuna$\cos^{-1}(\cos(5π/4))=\cos^{−1}(−\sqrt{2}/2))=3π/4$.
4. Tangu$\cos(2π/3)=−1/2$, tunahitaji kutathmini$\sin^{−1}(−1/2)$. Hiyo ni, tunahitaji kupata angle$θ$ kama hiyo$\sin(θ)=−1/2$ na$−π/2≤θ≤π/2$. Tangu$−π/6$ satisfies wote hali hizi, tunaweza kuhitimisha kwamba$\sin^{−1}(\cos(2π/3))=\sin^{−1}(−1/2)=−π/6.$

Thamani ya Juu ya Kazi

Katika maeneo mengi ya sayansi, uhandisi, na hisabati, ni muhimu kujua thamani ya kiwango cha juu kazi inaweza kupata, hata kama hatujui thamani yake halisi kwa papo fulani. Kwa mfano, ikiwa tuna kazi inayoelezea nguvu ya boriti ya paa, tunataka kujua uzito wa juu boriti inaweza kusaidia bila kuvunja. Ikiwa tuna kazi inayoelezea kasi ya treni, tungependa kujua kasi yake ya juu kabla ya kuruka kwenye reli. Muundo salama mara nyingi hutegemea kujua maadili ya juu.

Mradi huu inaeleza mfano rahisi wa kazi na thamani ya kiwango cha juu ambayo inategemea coefficients mbili equation. Tutaona kwamba maadili ya kiwango cha juu yanaweza kutegemea mambo kadhaa isipokuwa kutofautiana kwa kujitegemea$x$.

1. Fikiria grafu katika Kielelezo$\PageIndex{6}$ cha kazi$y=\sin x+\cos x.$ Eleza sura yake ya jumla. Je, ni mara kwa mara? Unajuaje?

Kielelezo$\PageIndex{6}$: grafu ya$y=\sin x+\cos x$.

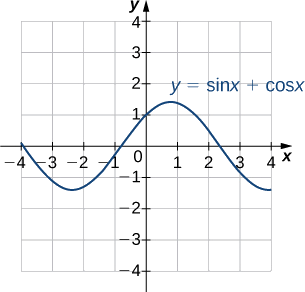
Kutumia calculator ya graphing au kifaa kingine cha kuchora, tathmini ya$x$ - na$y$ -maadili ya kiwango cha juu cha grafu (hatua ya kwanza ambapo$x > 0$). Inaweza kuwa na manufaa kwa kueleza$x$ -thamani kama nyingi ya$π.$

2. Sasa fikiria grafu nyingine za fomu$y=A\sin x+B\cos x$ kwa maadili mbalimbali ya$A$ na$B.$ Mchoro grafu wakati$A = 2$$B = 1,$ na kupata$x$ - na$y$ -maadili kwa kiwango cha juu. (Kumbuka kueleza$x$ -thamani kama nyingi ya$π$, ikiwezekana.) Je, ni wakiongozwa?

3. Rudia kwa$A = 1, \,B = 2.$ Je, kuna uhusiano wowote na kile ulichopata sehemu (2)?

4. Kukamilisha meza ifuatayo, kuongeza uchaguzi chache wa yako mwenyewe kwa ajili$A$ na$B:$

$A$	$B$	$x$	$y$	$A$	$B$	$x$	$y$
\ (A\)” style="wima align:katikati; "> 0	\ (B\)” style="wima align:katikati; "> 1	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">	\ (A\)” style="wima align:katikati; "> 3	\ (B\)” style="wima align:katikati; "> 4	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">
\ (A\)” style="wima align:katikati; "> 1	\ (B\)” style="wima align:katikati; "> 0	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">	\ (A\)” style="wima align:katikati; "> 4	\ (B\)” style="wima align:katikati; "> 3	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">
\ (A\)” style="wima align:katikati; "> 1	\ (B\)” style="wima align:katikati; "> 1	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">	\ (A\)” style="wima align:katikati; ">$\sqrt{3}$	\ (B\)” style="wima align:katikati; "> 1	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">
\ (A\)” style="wima align:katikati; "> 1	\ (B\)” style="wima align:katikati; "> 2	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">	\ (A\)” style="wima align:katikati; "> 1	\ (B\)” style="wima align:katikati; ">$\sqrt{3}$	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">
\ (A\)” style="wima align:katikati; "> 2	\ (B\)” style="wima align:katikati; "> 1	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">	\ (A\)” style="wima align:katikati; "> 12	\ (B\)” style="wima align:katikati; "> 5	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">
\ (A\)” style="wima align:katikati; "> 2	\ (B\)” style="wima align:katikati; "> 2	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">	\ (A\)” style="wima align:katikati; "> 5	\ (B\)” style="wima align:katikati; "> 12	\ (x\)” style="wima align:katikati; ">	\ (y\)” style="wima align:katikati; ">

5. Jaribu kufikiri formula kwa$y$ maadili -.

6. Fomu ya$x$ maadili ya -ni vigumu kidogo. Vipengele muhimu zaidi kutoka meza ni$(1,1),\, (1,\sqrt{3}),\, (\sqrt{3},1).$ (Kidokezo: Fikiria kazi za trigonometric inverse.)

7. Ikiwa umepata formula kwa sehemu (5) na (6), onyesha kwamba wanafanya kazi pamoja. Hiyo ni, badala ya$x$ formula ya thamani uliyoipata$y=A\sin x+B\cos x$ na kurahisisha ili kufika kwenye formula ya$y$ thamani uliyoipata.

Dhana muhimu

• Kwa kazi ya kuwa na inverse, kazi lazima iwe moja kwa moja. Kutokana na grafu ya kazi, tunaweza kuamua kama kazi ni moja kwa moja kwa kutumia mtihani wa mstari wa usawa.
• Ikiwa kazi sio moja kwa moja, tunaweza kuzuia kikoa kwenye uwanja mdogo ambapo kazi ni moja kwa moja na kisha kufafanua inverse ya kazi kwenye uwanja mdogo.
• Kwa kazi$f$ na inverse yake$f^{−1},\, f(f^{−1}(x))=x$ kwa ajili ya wote$x$ katika uwanja wa$f^{−1}$ na$f^{−1}(f(x))=x$ kwa ajili ya wote$x$ katika uwanja wa$f$.
• Kwa kuwa kazi za trigonometric ni mara kwa mara, tunahitaji kuzuia vikoa vyao ili kufafanua kazi za trigonometric inverse.
• Grafu ya kazi$f$ na inverse yake$f^{−1}$ ni sawa na mstari$y=x.$

Mlinganyo muhimu

• Kazi ya inverse

$f^{−1}(f(x))=x$kwa wote$x$ katika$D,$ na$f(f^{−1}(y))=y$ kwa ajili ya wote$y$ katika$R$.

faharasa

mtihani wa mstari wa usawa

kazi$f$ ni moja kwa moja ikiwa na tu ikiwa kila mstari wa usawa unaingilia grafu ya$f$, mara nyingi, mara moja

kazi inverse

kwa ajili ya kazi$f$, kazi inverse$f^{−1}$ satisfies$f^{−1}(y)=x$ kama$f(x)=y$

inverse trigonometric kazi

inverses ya kazi trigonometric hufafanuliwa kwenye vikoa vikwazo ambapo ni kazi moja kwa moja

kazi moja kwa moja

kazi$f$ ni moja kwa moja$f(x_1)≠f(x_2)$ ikiwa$x_1≠x_2$

kikoa kilichozuiliwa

subset ya uwanja wa kazi$f$