1.1: Mapitio ya Kazi
- Page ID
- 178953
- Tumia notation ya kazi ili kutathmini kazi.
- Kuamua uwanja na aina mbalimbali ya kazi.
- Chora grafu ya kazi.
- Kupata zeros ya kazi.
- Tambua kazi kutoka meza ya maadili.
- Fanya kazi mpya kutoka kwa kazi mbili au zaidi zilizopewa.
- Eleza mali ya ulinganifu wa kazi.
Katika sehemu hii, tunatoa ufafanuzi rasmi wa kazi na kuchunguza njia kadhaa ambazo kazi zinawakilishwa-yaani, kupitia meza, formula, na grafu. Tunasoma nukuu rasmi na masharti kuhusiana na kazi. Pia tunafafanua muundo wa kazi na mali za ulinganifu. Wengi wa nyenzo hii itakuwa mapitio kwako, lakini hutumikia kama kumbukumbu nzuri kukukumbusha baadhi ya mbinu za algebraic muhimu kwa kufanya kazi na kazi.
Kazi
Kutokana seti mbili\(A\) na\(B\) seti na mambo ambayo ni awali jozi\((x,y)\) ambapo\(x\) ni kipengele cha\(A\) na\(y\) ni kipengele cha\(B,\) ni uhusiano kutoka\(A\) kwa\(B\). Uhusiano kutoka\(A\) kwa\(B\) hufafanua uhusiano kati ya seti hizo mbili. Kazi ni aina maalum ya uhusiano ambayo kila kipengele cha kuweka kwanza kinahusiana na kipengele kimoja cha seti ya pili. Kipengele cha seti ya kwanza kinaitwa pembejeo; kipengele cha seti ya pili inaitwa pato. Kazi zinatumika wakati wote katika hisabati kuelezea mahusiano kati ya seti mbili. Kwa kazi yoyote, tunapojua pembejeo, pato imedhamiriwa, kwa hiyo tunasema kwamba pato ni kazi ya pembejeo. Kwa mfano, eneo la mraba linatambuliwa na urefu wake wa upande, kwa hiyo tunasema kwamba eneo (pato) ni kazi ya urefu wake wa upande (pembejeo). Upeo wa mpira uliotupwa hewani unaweza kuelezewa kama kazi ya kiasi cha muda mpira ulipo hewani. Gharama ya barua pepe ya mfuko ni kazi ya uzito wa mfuko. Kwa kuwa kazi zina matumizi mengi, ni muhimu kuwa na ufafanuzi sahihi na istilahi ili kuzifunza.

Kazi\(f\) ina seti ya pembejeo, seti ya matokeo, na utawala wa kumshirikisha kila pembejeo kwa pato moja hasa. Seti ya pembejeo inaitwa uwanja wa kazi. Seti ya matokeo inaitwa aina mbalimbali za kazi.
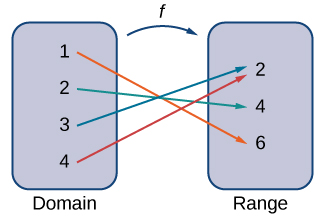
Kwa mfano, fikiria kazi\(f\), ambapo uwanja ni seti ya namba zote halisi na utawala ni mraba pembejeo. Kisha, pembejeo\(x=3\) hutolewa kwa pato\(3^2=9\).
Kwa kuwa kila nambari halisi isiyo ya kawaida ina mizizi halisi ya mraba, kila nambari isiyo ya kawaida ni kipengele cha kazi hii. Kwa kuwa hakuna namba halisi na mraba ambayo ni hasi, namba halisi hasi sio vipengele vya upeo. Tunahitimisha kuwa upeo ni seti ya nambari halisi zisizo na hasi.
Kwa kazi ya jumla\(f\) na kikoa\(D\), mara nyingi tunatumia\(x\) kutaja pembejeo na\(y\) kutaja pato linalohusishwa na\(x\). Wakati wa kufanya hivyo, sisi rejea\(x\) kama variable huru na\(y\) kama variable tegemezi, kwa sababu inategemea\(x\). Kutumia kazi nukuu, sisi kuandika\(y=f(x)\), na sisi kusoma equation hii kama “\(y\)sawa\(f\) ya\(x.”\) Kwa kazi squaring ilivyoelezwa hapo awali, sisi kuandika\(f(x)=x^2\).
Dhana ya kazi inaweza visualized kwa kutumia Takwimu\(\PageIndex{1}\) -\(\PageIndex{3}\).
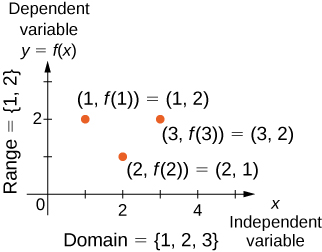
Pia tunaweza taswira kazi kwa njama pointi\((x,y)\) katika kuratibu ndege ambapo\(y=f(x)\). Grafu ya kazi ni seti ya pointi hizi zote. Kwa mfano, fikiria kazi\(f\), ambapo uwanja ni kuweka\(D=\{1,2,3\}\) na utawala ni\(f(x)=3−x\). Katika Kielelezo\(\PageIndex{4}\), tunapanga grafu ya kazi hii.
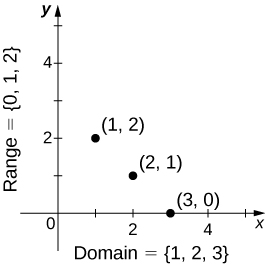
Kila kazi ina uwanja. Hata hivyo, wakati mwingine kazi inaelezewa na equation, kama\(f(x)=x^2\) ilivyo, bila uwanja maalum uliotolewa. Katika kesi hii, uwanja unachukuliwa kuwa seti ya namba\(x\) zote halisi ambazo\(f(x)\) ni namba halisi. Kwa mfano, kwa kuwa nambari yoyote halisi inaweza kuwa mraba, ikiwa hakuna uwanja mwingine ulioelezwa, tunaona uwanja wa\(f(x)=x^2\) kuwa seti ya namba zote halisi. Kwa upande mwingine, kazi ya mizizi ya mraba inatoa\(f(x)=\sqrt{x}\) tu pato halisi ikiwa\(x\) sio hasi. Kwa hiyo, uwanja wa kazi\(f(x)=\sqrt{x}\) ni seti ya nambari halisi zisizo na hasi, wakati mwingine huitwa uwanja wa asili.
Kwa kazi\(f(x)=x^2\) na\(f(x)=\sqrt{x}\), vikoa vinawekwa na idadi isiyo na kipimo cha vipengele. Ni wazi hatuwezi kuorodhesha mambo haya yote. Wakati wa kuelezea seti na idadi isiyo na kipimo cha vipengele, mara nyingi husaidia kutumia wajenzi wa kuweka-au notation ya muda. Wakati wa kutumia nukuu ya wajenzi wa kuweka kuelezea subset ya namba zote halisi, zilizoashiria\(R\), tunaandika
\[\{x\,|\,\textit{x has some property}\}. \nonumber \]
Tunasoma hii kama seti ya namba halisi\(x\) kama hiyo\(x\) ina mali fulani. Kwa mfano, ikiwa tulikuwa na nia ya seti ya namba halisi ambazo ni kubwa zaidi ya moja lakini chini ya tano, tunaweza kuashiria seti hii kwa kutumia nukuu ya wajenzi wa kuweka kwa kuandika
\[\{x\,|\,1<x<5\}.\nonumber \]
Seti kama hii, ambayo ina namba zote kubwa kuliko\(a\) na chini ya\(b,\) inaweza pia kutajwa kwa kutumia notation ya muda\((a,b)\). Kwa hiyo,
\[(1,5)=\{x\,|\,1<x<5\}.\nonumber \]
Nambari\(1\) na\(5\) huitwa mwisho wa seti hii. Ikiwa tunataka kuzingatia seti inayojumuisha mwisho, tutaashiria kuweka hii kwa kuandika
\[[1,5]=\{x\,|\,1 \le x \le 5\}.\nonumber \]
Tunaweza kutumia notation sawa kama tunataka ni pamoja na moja ya endpoints, lakini si nyingine. Ili kutaja seti ya nambari halisi zisizo na hasi, tunataka kutumia notation ya kuweka-wajenzi
\[\{x\,|\,x\ge 0\}.\nonumber \]
Nambari ndogo zaidi katika seti hii ni sifuri, lakini seti hii haina idadi kubwa zaidi. Kutumia muda nukuu, tunataka kutumia ishara\(∞,\) ambayo inahusu infinity chanya, na tunataka kuandika kuweka kama
\[[0,∞)=\{x\,|\,x\ge 0\}.\nonumber \]
Ni muhimu kutambua kwamba\(∞\) si idadi halisi. Inatumiwa kwa mfano hapa kuonyesha kwamba seti hii inajumuisha namba zote halisi zaidi kuliko au sawa na sifuri. Vile vile, kama tulitaka kuelezea seti ya namba zote nonpositive, tunaweza kuandika
\[(−∞,0]=\{x\,|\,x≤0\}.\nonumber \]
Hapa, notation\(−∞\) inahusu infinity hasi, na inaonyesha kwamba sisi ni pamoja na idadi yote chini ya au sawa na sifuri, bila kujali jinsi ndogo. Seti
\[(−∞,∞)=\{\textit{x} \,|\, \textit{x is any real number}\}\nonumber \]
inahusu seti ya namba zote halisi. Baadhi ya kazi hufafanuliwa kwa kutumia equations tofauti kwa sehemu tofauti za uwanja wao. Aina hizi za kazi zinajulikana kama kazi zilizoelezwa kwa kipande. Kwa mfano, tuseme tunataka kufafanua kazi\(f\) na uwanja kwamba ni seti ya namba zote halisi kama kwamba\(f(x)=3x+1\) kwa\(x≥2\) na\(f(x)=x^2\) kwa\( x<2\). Tunaashiria kazi hii kwa kuandika
\[f(x)=\begin{cases} 3x+1, & \text{if } x≥2 \\ x^2, & \text{if } x<2 \end{cases}\nonumber \]
Wakati wa kutathmini kazi hii kwa pembejeo\(x\), equation ya kutumia inategemea kama\(x≥2\) au\(x<2\). Kwa mfano, tangu\(5>2\), tunatumia ukweli kwamba\(f(x)=3x+1\) kwa\(x≥2\) na kuona hiyo\(f(5)=3(5)+1=16\). Kwa upande mwingine, kwa\(x=−1\), sisi kutumia ukweli kwamba\(f(x)=x^2\) kwa\(x<2\) na kuona kwamba\(f(−1)=1\).
Kwa kazi\(f(x)=3x^2+2x−1\), tathmini:
- \(f(−2)\)
- \(f(\sqrt{2})\)
- \(f(a+h)\)
Suluhisho
Badilisha thamani iliyotolewa\(x\) kwa formula kwa\(f(x)\).
- \(f(−2)=3(−2)^2+2(−2)−1=12−4−1=7\)
- \(f(\sqrt{2})=3(\sqrt{2})^2+2\sqrt{2}−1=6+2\sqrt{2}−1=5+2\sqrt{2}\)
- \(f(a+h)=3(a+h)^2+2(a+h)−1=3(a^2+2ah+h^2)+2a+2h−1=3a^2+6ah+3h^2+2a+2h−1\)
Kwa\(f(x)=x^2−3x+5\), tathmini\(f(1)\) na\(f(a+h)\).
- Kidokezo
-
Mbadala\(1\) na\(a+h\)\(x\) kwa formula kwa\(f(x)\).
- Jibu
-
\(f(1)=3 \)na\(f(a+h)=a^2+2ah+h^2−3a−3h+5\)
Kwa kila moja ya kazi zifuatazo, tambua i. kikoa na ii. mbalimbali.
- \(f(x)=(x−4)^2+5\)
- \(f(x)=\sqrt{3x+2}−1\)
- \(f(x)=\dfrac{3}{x−2}\)
Suluhisho
a. fikiria\(f(x)=(x−4)^2+5.\)
1.Tangu\(f(x)=(x−4)^2+5\) ni namba halisi kwa idadi yoyote halisi\(x\), uwanja wa\(f\) ni muda\((−∞,∞)\).
2. Tangu\((x−4)^2≥0\), tunajua\(f(x)=(x−4)^2+5≥5\). Kwa hiyo, mbalimbali lazima subset ya\(\{y\,|\,y≥5\}.\) Kuonyesha kwamba kila kipengele katika kuweka hii ni katika mbalimbali, tunahitaji kuonyesha kwamba kwa kutolewa\(y\) katika kuweka kwamba, kuna idadi halisi\(x\) kama hiyo\(f(x)=(x−4)^2+5=y\). Kutatua equation hii kwa\(x,\) tunaona kwamba tunahitaji\(x\) vile
\((x−4)^2=y−5.\)
Equation hii ni kuridhika kwa muda mrefu kama kuna idadi halisi\(x\) kama kwamba
\(x−4=±\sqrt{y−5}\)
Tangu\(y≥5\), mizizi ya mraba imefafanuliwa vizuri. Tunahitimisha kuwa kwa hiyo\(x=4±\sqrt{y−5},\)\(f(x)=y,\) na kwa hiyo ni\(\{y\,|\,y≥5 \}.\)
b Fikiria\(f(x)=\sqrt{3x+2}−1\).
1.Ili kupata uwanja wa\(f\), tunahitaji kujieleza\(3x+2≥0\). Kutatua usawa huu, tunahitimisha kuwa uwanja ni\(\{x\,|\,x≥−2/3\}.\)
2.Ili kupata mbalimbali ya\(f\), tunaona kwamba tangu\(\sqrt{3x+2}≥0,\)\(f(x)=\sqrt{3x+2}−1≥−1\). Kwa hiyo, aina ya\(f\) lazima iwe subset ya kuweka\(\{y\,|\,y≥−1\}\). Kuonyesha kwamba kila kipengele katika seti hii ni katika aina mbalimbali ya\(f\), tunahitaji kuonyesha kwamba kwa wote\(y\) katika kuweka hii, kuna idadi halisi\(x\) katika uwanja kama kwamba\(f(x)=y.\) Hebu\(y≥−1.\) Kisha,\(f(x)=y\) ikiwa na tu kama
\(\sqrt{3x+2}−1=y.\)
Kutatua equation hii kwa\(x,\) tunaona kwamba\(x\) lazima kutatua equation
\(\sqrt{3x+2}=y+1.\)
Tangu\(y≥−1\), kama\(x\) inaweza kuwepo. Squaring pande zote mbili za equation hii, tuna\(3x+2=(y+1)^2.\)
Kwa hiyo, tunahitaji
\(3x=(y+1)^2−2,\)
ambayo ina maana
\(x=\frac{1}{3}(y+1)^2−\frac{2}{3}.\)
Tunahitaji tu kuthibitisha kwamba\(x\) ni katika uwanja wa\(f\). Tangu uwanja wa\(f\) lina idadi yote halisi zaidi au sawa na\(\frac{−2}{3}\), na
\(\frac{1}{3}(y+1)^2-\frac{2}{3}≥−\frac{2}{3},\)
kuna gani zipo\(x\) katika uwanja wa\(f\). Sisi kuhitimisha kwamba mbalimbali ya\(f\) ni\(\{y\,|\,y≥−1\}.\)
c Fikiria\(f(x)=\dfrac{3}{x−2}.\)
1.Kwa kuwa\(3/(x−2)\) inafafanuliwa wakati denominator ni nonzero, uwanja ni\(\{x\,|\,x≠2\}.\)
2.Ili kupata aina mbalimbali ya\(f,\) tunahitaji kupata maadili ya\(y\) vile kwamba kuna idadi halisi\(x\) katika uwanja na mali ambayo
\(\dfrac{3}{x−2}=y.\)
Kutatua equation hii kwa\(x,\) tunaona kwamba
\(x=\dfrac{3}{y}+2.\)
Kwa hiyo, kwa muda mrefu kama\(y≠0\), kuna idadi halisi\(x\) katika uwanja huo\(f(x)=y\). Hivyo, mbalimbali ni\(\{y\,|\,y≠0\}.\)
Pata kikoa na upeo\(f(x)=\sqrt{4−2x}+5.\)
- Kidokezo
-
Tumia\(4−2x≥0\).
- Jibu
-
Domain =\(\{x\,|\,x≤2\}\) na upeo =\(\{y\,|\,y≥5\}\)
Kazi zinazowakilisha
Kwa kawaida, kazi inawakilishwa kwa kutumia moja au zaidi ya zana zifuatazo:
- Jedwali
- Grafu
- Fomu
Tunaweza kutambua kazi katika kila aina, lakini tunaweza pia kuzitumia pamoja. Kwa mfano, tunaweza kupanga kwenye grafu maadili kutoka meza au kuunda meza kutoka kwa formula.
Majedwali
Kazi zilizoelezwa kwa kutumia meza ya maadili hutokea mara kwa mara katika programu halisi ya ulimwengu. Fikiria mfano wafuatayo rahisi. Tunaweza kuelezea joto siku fulani kama kazi ya wakati wa siku. Tuseme tunarekodi joto kila saa kwa kipindi cha saa 24 kuanzia usiku wa manane. Sisi basi pembejeo yetu variable\(x\) kuwa wakati baada ya usiku wa manane, kipimo katika masaa, na variable pato\(y\) kuwa\(x\) masaa joto baada ya usiku wa manane, kipimo katika digrii Fahrenheit. Tunarekodi data yetu katika Jedwali\(\PageIndex{1}\).
| Saa baada ya usiku wa manane | Joto (°F) | Saa baada ya usiku wa manane | Joto (°F) |
|---|---|---|---|
| 0 | 58 | 12 | 84 |
| 1 | 54 | 13 | 85 |
| 2 | 53 | 14 | 85 |
| 3 | 52 | 15 | 83 |
| 4 | 52 | 16 | 82 |
| 5 | 55 | 17 | 80 |
| 6 | 60 | 18 | 77 |
| 7 | 64 | 19 | 74 |
| 8 | 72 | 20 | 69 |
| 9 | 75 | 21 | 65 |
| 10 | 78 | 22 | 60 |
| 11 | 80 | 23 | 58 |
Tunaweza kuona kutoka meza kwamba joto ni kazi ya muda, na joto hupungua, kisha huongezeka, halafu hupungua tena. Hata hivyo, hatuwezi kupata picha wazi ya tabia ya kazi bila graphing yake.
Grafu
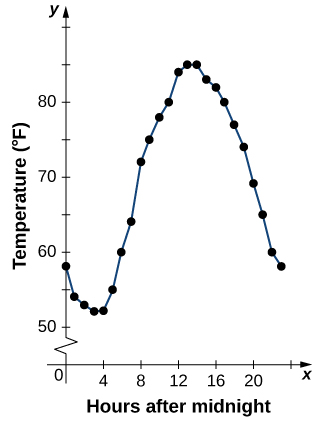
Kutokana na kazi\(f\) iliyoelezwa na meza, tunaweza kutoa picha ya kuona ya kazi kwa namna ya grafu. Graphing joto waliotajwa katika Jedwali\(\PageIndex{1}\) inaweza kutupa wazo bora ya kushuka kwa thamani yao siku nzima. Kielelezo\(\PageIndex{5}\) kinaonyesha njama ya kazi ya joto.
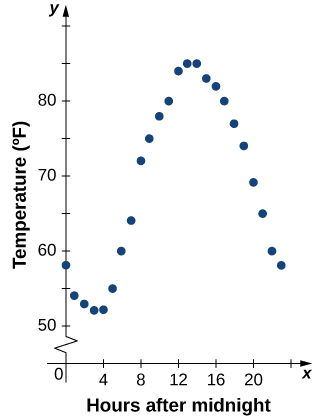
Kutoka kwa pointi zilizopangwa kwenye grafu kwenye Mchoro\(\PageIndex{5}\), tunaweza kutazama sura ya jumla ya grafu. Mara nyingi ni muhimu kuunganisha dots kwenye grafu, ambayo inawakilisha data kutoka meza. Katika mfano huu, ingawa hatuwezi kufanya hitimisho lolote kuhusu hali ya joto ilikuwa wakati wowote ambayo joto halikurekodi, kutokana na idadi ya pointi data zilizokusanywa na muundo katika pointi hizi, ni busara kwa mtuhumiwa kuwa joto wakati mwingine ikifuatiwa mfano sawa, kama tunaweza kuona katika Kielelezo\(\PageIndex{6}\).
Aljebraic Formula
Wakati mwingine sisi si kupewa maadili ya kazi katika fomu meza, badala sisi ni kupewa maadili katika formula wazi. Fomu zinatokea katika programu nyingi. Kwa mfano, eneo la mduara wa radius\(r\) hutolewa na formula\(A(r)=πr^2\). Wakati kitu kinatupwa juu kutoka chini kwa kasi ya awali\(v_{0}\) ft/s, urefu wake juu ya ardhi kutoka wakati unapotupwa mpaka unapopiga ardhi hutolewa na formula\(s(t)=−16t^2+v_{0}t\). Wakati\(P\) dola zimewekeza katika akaunti kwa kiwango cha riba ya kila\(r\) mwaka kinachozidi kuendelea, kiasi cha fedha baada ya\(t\) miaka kinatolewa na formula\(A(t)=Pe^{rt}\). Fomu za algebraic ni zana muhimu za kuhesabu maadili ya kazi. Mara nyingi sisi pia tunawakilisha kazi hizi kuibua katika fomu ya grafu.
Kutokana formula algebraic kwa ajili ya kazi\(f\), grafu ya\(f\) ni seti ya pointi\((x,f(x))\), ambapo\(x\) ni katika uwanja wa\(f\) na\(f(x)\) ni katika mbalimbali. Ili kuchora kazi iliyotolewa na formula, ni muhimu kuanza kwa kutumia formula ili kuunda meza ya pembejeo na matokeo. Ikiwa uwanja wa\(f\) lina idadi isiyo na kipimo cha maadili, hatuwezi kuorodhesha wote, lakini kwa sababu orodha ya baadhi ya pembejeo na matokeo inaweza kuwa muhimu sana, mara nyingi ni njia nzuri ya kuanza.
Wakati wa kujenga meza ya pembejeo na matokeo, sisi kawaida kuangalia kuamua kama sifuri ni pato. Maadili hayo ya\(x\) wapi\(f(x)=0\) huitwa zeros ya kazi. Kwa mfano, zero za\(f(x)=x^2−4\) ni\(x=±2\). Zero huamua ambapo grafu ya\(f\) intersects\(x\) -axis, ambayo inatupa habari zaidi kuhusu sura ya grafu ya kazi. Grafu ya kazi haiwezi kamwe kuingiliana\(x\) -axis, au inaweza kuingiliana mara nyingi (au hata nyingi sana).
Jambo lingine la maslahi ni\(y\) -intercept, ikiwa ipo. \(y\)-Intercept inatolewa na\((0,f(0))\).
Kwa kuwa kazi ina pato moja kwa kila pembejeo, grafu ya kazi inaweza kuwa na, zaidi,\(y\) moja-intercept. Kama\(x=0\) ni katika uwanja wa kazi\(f,\) basi\(f\) ina hasa moja\(y\) -intercept. Kama\(x=0\) si katika uwanja wa\(f,\) basi\(f\) hana\(y\) -intercept. Vile vile, kwa idadi yoyote halisi\(c,\) ikiwa\(c\) iko katika uwanja wa\(f\), kuna pato moja\(f(c),\) na mstari\(x=c\) unaingilia grafu ya\(f\) mara moja. Kwa upande mwingine, kama\(c\) si katika uwanja wa\(f,\)\(f(c)\) si defined na line\(x=c\) haina intersect grafu ya\(f\). Mali hii ni muhtasari katika mtihani wa mstari wa wima.
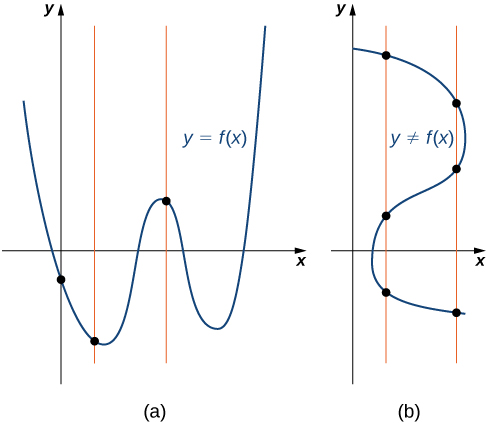
Kutokana na kazi\(f\), kila mstari wa wima ambao unaweza kupatikana huingilia kati ya grafu ya\(f\) si zaidi ya mara moja. Ikiwa mstari wowote wa wima unaingilia seti ya pointi zaidi ya mara moja, seti ya pointi haiwakilishi kazi.
Tunaweza kutumia mtihani huu kuamua kama seti ya pointi zilizopangwa inawakilisha grafu ya kazi (Kielelezo\(\PageIndex{7}\)).
Fikiria kazi\(f(x)=−4x+2.\)
- Kupata zeros wote wa\(f\).
- Pata\(y\) -intercept (kama ipo).
- Mchoro grafu ya\(f\).
Suluhisho
1.Ili kupata zero, tatua\(f(x)=−4x+2=0\). Sisi kugundua kwamba\(f\) ina sifuri moja katika\(x=1/2\).
2. \(y\)Kizuizi kinachotolewa na\((0,f(0))=(0,2).\)
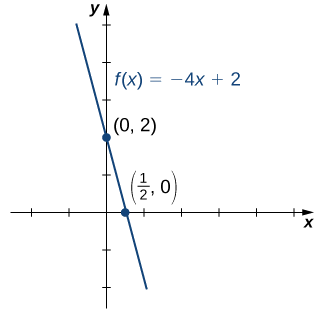
3. Kutokana na kwamba\(f\) ni kazi linear ya fomu\(f(x)=mx+b\) ambayo hupita kupitia pointi\((1/2,0)\) na\((0,2)\), tunaweza mchoro grafu ya\(f\) (Kielelezo\(\PageIndex{8}\)).
Fikiria kazi\(f(x)=\sqrt{x+3}+1\).
- Kupata zeros wote wa\(f\).
- Pata\(y\) -intercept (kama ipo).
- Mchoro grafu ya\(f\).
Suluhisho
1.Ili kupata zero, tatua\(\sqrt{x+3}+1=0\). Equation hii ina maana\(\sqrt{x+3}=−1\). Tangu\(\sqrt{x+3}≥0\) kwa wote\(x\), equation hii haina ufumbuzi, na kwa hiyo\(f\) haina zero.
2.\(y\) intercept inatolewa na\((0,f(0))=(0,\sqrt{3}+1)\).
3.Ili kuchora kazi hii, tunafanya meza ya maadili. Tangu tunahitaji\(x+3≥0\), tunahitaji kuchagua maadili ya\(x≥−3\). Tunachagua maadili ambayo hufanya kazi ya mizizi ya mraba iwe rahisi kutathmini.
| \(x\) | -3 | -2 | 1 |
|---|---|---|---|
| \(f(x)\) | 1 | 2 | 3 |
Kufanya matumizi ya meza na kujua kwamba, kwa kuwa kazi ni mizizi ya mraba, grafu ya\(f\) inapaswa kuwa sawa na grafu ya\(y=\sqrt{x}\), sisi mchoro grafu (Kielelezo\(\PageIndex{9}\)).
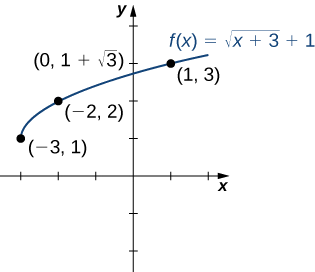
Kupata zeros ya\(f(x)=x^3−5x^2+6x.\)
- Kidokezo
-
Sababu ya polynomial.
- Jibu
-
\(x=0,2,3\)
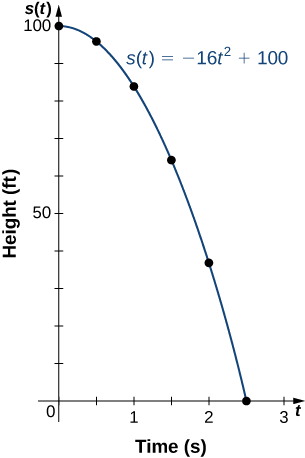
Ikiwa mpira umeshuka kutoka urefu wa futi 100, urefu wake s kwa wakati\(t\) unatolewa na kazi\(s(t)=−16t^2+100\), ambapo s hupimwa kwa miguu na\(t\) hupimwa kwa sekunde. Domain ni vikwazo kwa muda\([0,c],\) ambapo\(t=0\) ni wakati ambapo mpira ni imeshuka na\(t=c\) ni wakati ambapo mpira hits chini.
- Kujenga meza kuonyesha urefu s (t) wakati\(t=0,\, 0.5,\, 1,\, 1.5,\, 2,\) na\(2.5\). Kutumia data kutoka meza, tambua kikoa cha kazi hii. Hiyo ni, kupata\(c\) wakati ambapo mpira unapiga chini.
- Mchoro grafu ya\(s\).
Suluhisho
| \(t\) | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 |
| \(s(t)\) | 100 | 96 | 84 | 64 | 36 | 0 |
Tangu mpira hupiga ardhi wakati\(t=2.5\), uwanja wa kazi hii ni muda\([0,2.5]\).
2.
Tunasema kuwa kazi\(f\) inaongezeka kwa muda\(I\) ikiwa kwa wote\(x_{1},\, x_{2}∈I,\)
\(f(x_{1})≤f(x_{2})\)lini\(x_{1}<x_{2}.\)
Tunasema\(f\) ni madhubuti kuongezeka kwa muda\(I\) kama kwa wote\(x_{1},x_{2}∈I,\)
\(f(x_{1})<f(x_{2})\)lini\(x_{1}<x_{2}.\)
Tunasema kuwa kazi\(f\) inapungua kwa muda\(I\) ikiwa kwa wote\(x_{1},x_{2}∈I,\)
\(f(x_{1})≥f(x_{2})\)kama\(x_{1}<x_{2}.\)
Tunasema kwamba kazi\(f\) ni madhubuti kupungua kwa muda\(I\) kama kwa wote\(x_{1},x_{2}∈I\),
\(f(x_{1})>f(x_{2})\)kama\(x_{1}<x_{2}.\)
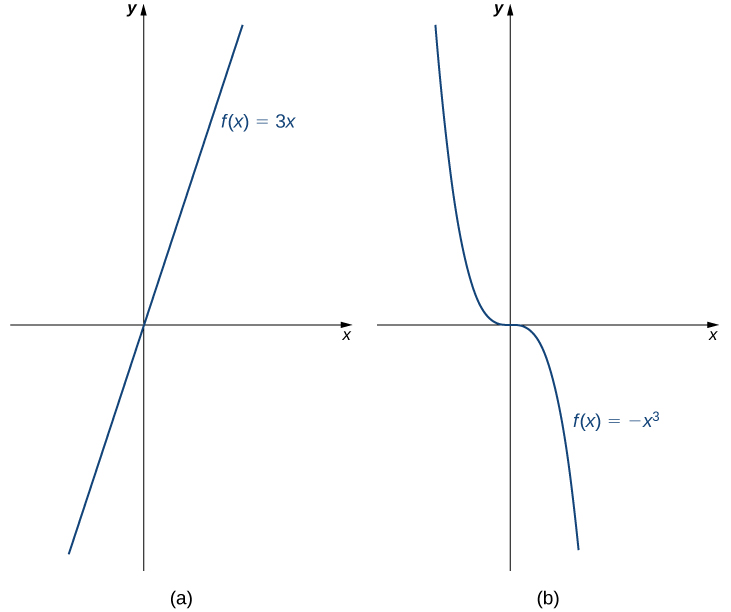
Kwa mfano, kazi\(f(x)=3x\) inaongezeka kwa muda kwa\((−∞,∞)\) sababu\(3x_{1}<3x_{2}\) wakati wowote\(x_{1}<x_{2}\). Kwa upande mwingine, kazi\(f(x)=−x^3\) ni kupungua kwa muda\((−∞,∞)\) kwa sababu wakati\(−x^3_{1}>−x^3_{2}\) wowote\(x_{1}<x_{2}\) (Kielelezo\(\PageIndex{10}\)).
Kuchanganya Kazi
Sasa kwa kuwa tumepitia upya sifa za msingi za kazi, tunaweza kuona nini kinatokea kwa mali hizi tunapochanganya kazi kwa njia tofauti, kwa kutumia shughuli za msingi za hisabati ili kuunda kazi mpya. Kwa mfano, ikiwa gharama ya kampuni ya kutengeneza\(x\) vitu inaelezewa\(C(x)\) na kazi na mapato yaliyoundwa na uuzaji wa\(x\) vitu yanaelezwa na kazi\(R(x)\), basi faida ya utengenezaji na uuzaji wa\(x\) vitu hufafanuliwa kama\(P(x)=R(x)−C(x)\). Kutumia tofauti kati ya kazi mbili, tumeunda kazi mpya.
Vinginevyo, tunaweza kuunda kazi mpya kwa kutunga kazi mbili. Kwa mfano, kutokana\(f(x)=x^2\) na kazi na\(g(x)=3x+1\), kazi Composite\(f∘g\) ni defined kama
\[(f∘g)(x)=f(g(x))=(g(x))^2=(3x+1)^2. \nonumber \]
Kazi ya composite\(g∘f\) inaelezwa kama vile
\[(g∘f)(x)=g(f(x))=3f(x)+1=3x^2+1. \nonumber \]
Kumbuka kuwa kazi hizi mbili mpya ni tofauti na kila mmoja.
Kuchanganya Kazi na Wafanyakazi wa Hisabati
Ili kuchanganya kazi kwa kutumia waendeshaji wa hisabati, tunaandika tu kazi na operator na kurahisisha. Kutokana\(f\) na kazi mbili na\(g\), tunaweza kufafanua kazi nne mpya:
| \((f+g)(x)=f(x)+g(x)\) | Jumla |
| \((f−g)(x)=f(x)−g(x)\) | Tofauti |
| \((f·g)(x)=f(x)g(x)\) | Bidhaa |
| \((\frac{f}{g})(x)=\frac{f(x)}{g(x)}\)kwa\(g(x)≠0\) | Quotient |
Kutokana na kazi\(f(x)=2x−3\) na\(g(x)=x^2−1\), tafuta kila kazi zifuatazo na ueleze kikoa chake.
- \((f+g)(x)\)
- \((f−g)(x)\)
- \((f·g)(x)\)
- \(\left(\dfrac{f}{g}\right)(x)\)
Suluhisho
1. \((f+g)(x)=(2x−3)+(x^2−1)=x^2+2x−4.\)
Kikoa cha kazi hii ni muda\((−∞,∞)\).
2. \((f−g)(x)=(2x−3)−(x^2−1)=−x^2+2x−2.\)
Kikoa cha kazi hii ni muda\((−∞,∞)\).
3. \((f·g)(x)=(2x−3)(x^2−1)=2x^3−3x^2−2x+3.\)
Kikoa cha kazi hii ni muda\((−∞,∞)\).
4. \(\left(\dfrac{f}{g}\right)(x)=\dfrac{2x−3}{x^2−1}\).
Kikoa cha kazi hii ni\(\{x\,|\,x≠±1\}.\)
Kwa\(f(x)=x^2+3\) na\(g(x)=2x−5\), tafuta\((f/g)(x)\) na ueleze kikoa chake.
- Kidokezo
-
Kazi mpya\((f/g)(x)\) ni quotient ya kazi mbili. Kwa nini maadili ya\(x\) ni denominator sifuri?
- Jibu
-
\(\left(\dfrac{f}{g}\right)(x)=\frac{x^2+3}{2x−5}.\)Kikoa ni\(\{x\,|\,x≠\frac{5}{2}\}.\)
Utungaji wa Kazi
Wakati sisi kutunga kazi, sisi kuchukua kazi ya kazi. Kwa mfano, tuseme joto\(T\) kwenye siku fulani linaelezewa kama kazi ya muda\(t\) (kipimo kwa masaa baada ya usiku wa manane) kama ilivyo kwenye Jedwali\(\PageIndex{1}\). Tuseme gharama\(C\), kwa joto au baridi jengo kwa saa 1, inaweza kuelezewa kama kazi ya joto\(T\). Kuchanganya kazi hizi mbili, tunaweza kuelezea gharama ya kupokanzwa au kuimarisha jengo kama kazi ya muda kwa kutathmini\(C(T(t))\). Sisi defined kazi mpya, ulionyehsa\(C∘T\), ambayo ni defined vile kwamba\((C∘T)(t)=C(T(t))\) kwa wote\(t\) katika uwanja wa\(T\). Kazi hii mpya inaitwa kazi ya composite. Tunaona kwamba kwa kuwa gharama ni kazi ya joto na joto ni kazi ya muda, ni busara kufafanua kazi hii mpya\((C∘T)(t)\). Haina maana ya kuzingatia\((T∘C)(t)\), kwa sababu joto sio kazi ya gharama.
Fikiria kazi\(f\) na kikoa\(A\) na upeo\(B\), na kazi\(g\) na kikoa\(D\) na upeo\(E\). Kama\(B\) ni subset ya\(D\), basi kazi Composite\((g∘f)(x)\) ni kazi na uwanja\(A\) kama kwamba
\[(g∘f)(x)=g(f(x)) \nonumber \]
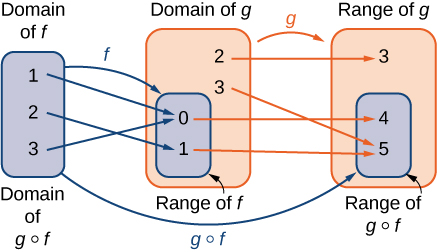
Kazi ya composite\(g∘f\) inaweza kutazamwa katika hatua mbili. Kwanza, kazi\(f\) ramani kila pembejeo\(x\) katika uwanja wa\(f\) kwa pato lake\(f(x)\) katika aina mbalimbali ya\(f\). Pili, tangu mbalimbali ya\(f\) ni subset ya uwanja wa\(g\), pato\(f(x)\) ni kipengele katika uwanja wa\(g\), na kwa hiyo ni mapped kwa pato\(g(f(x))\) katika aina mbalimbali ya\(g\). Katika Kielelezo\(\PageIndex{11}\), tunaona picha ya kuona ya kazi ya composite.
Fikiria kazi\(f(x)=x^2+1\) na\(g(x)=1/x\).
- Pata\((g∘f)(x)\) na useme kikoa chake na upeo.
- Tathmini\((g∘f)(4),\)\((g∘f)(−1/2)\).
- Pata\((f∘g)(x)\) na useme kikoa chake na upeo.
- Tathmini\((f∘g)(4),\)\((f∘g)(−1/2)\).
Suluhisho
1. Tunaweza kupata formula\((g∘f)(x)\) kwa njia mbili tofauti. Tunaweza kuandika
\((g∘f)(x)=g(f(x))=g(x^2+1)=\dfrac{1}{x^2+1}\).
Vinginevyo, tunaweza kuandika
\((g∘f)(x)=g(f(x))=\dfrac{1}{f(x)}=\dfrac{1}{x^2+1}.\)
Tangu\(x^2+1≠0\) kwa namba zote halisi uwanja\(x,\) wa\((g∘f)(x)\) ni seti ya namba zote halisi. Tangu\(0<1/(x^2+1)≤1\), upeo ni, kwa zaidi, muda\((0,1]\). Kuonyesha kwamba mbalimbali ni kipindi hiki nzima, sisi basi\(y=1/(x^2+1)\) na kutatua equation hii\(x\) kwa kuonyesha kwamba kwa wote\(y\) katika kipindi\((0,1]\), kuna idadi halisi\(x\) kama hiyo\(y=1/(x^2+1)\). Kutatua equation hii kwa\(x,\) tunaona kwamba\(x^2+1=1/y\), ambayo ina maana kwamba
\(x=±\sqrt{\frac{1}{y}−1}\)
Ikiwa\(y\) ni katika kipindi\((0,1]\), maneno chini ya radical ni yasiyo ya negative, na kwa hiyo kuna idadi halisi\(x\) kama hiyo\(1/(x^2+1)=y\). Sisi kuhitimisha kwamba mbalimbali ya\(g∘f\) ni muda\((0,1].\)
2. \((g∘f)(4)=g(f(4))=g(4^2+1)=g(17)=\frac{1}{17}\)
\((g∘f)(−\frac{1}{2})=g(f(−\frac{1}{2}))=g((−\frac{1}{2})^2+1)=g(\frac{5}{4})=\frac{4}{5}\)
3. Tunaweza kupata formula\((f∘g)(x)\) kwa njia mbili. Kwanza, tunaweza kuandika
\((f∘g)(x)=f(g(x))=f(\frac{1}{x})=(\frac{1}{x})^2+1.\)
Vinginevyo, tunaweza kuandika
\((f∘g)(x)=f(g(x))=(g(x))^2+1=(\frac{1}{x})^2+1.\)
Domain ya\(f∘g\) ni seti ya namba zote halisi\(x\) kama hiyo\(x≠0\). Ili kupata aina mbalimbali\(f,\) tunahitaji kupata maadili\(y\) yote ambayo kuna idadi halisi\(x≠0\) kama hiyo
\(\left(\dfrac{1}{x}\right)^2+1=y.\)
Kutatua equation hii kwa\(x,\) tunaona kwamba tunahitaji\(x\) kukidhi
\(\left(\dfrac{1}{x}\right)^2=y−1,\)
ambayo simplifies kwa
\(\dfrac{1}{x}=±\sqrt{y−1}\)
Hatimaye, sisi kupata
\(x=±\dfrac{1}{\sqrt{y−1}}.\)
Tangu\(1/\sqrt{y−1}\) ni idadi halisi kama na tu kama mbalimbali\(y>1,\) ya\(f\) ni kuweka\(\{y\,|\,y≥1\}.\)
4. \((f∘g)(4)=f(g(4))=f(\frac{1}{4})=(\frac{1}{4})^2+1=\frac{17}{16}\)
\((f∘g)(−\frac{1}{2})=f(g(−\frac{1}{2}))=f(−2)=(−2)^2+1=5\)
Katika Mfano\(\PageIndex{7}\), tunaweza kuona hilo\((f∘g)(x)≠(g∘f)(x)\). Hii inatuambia, kwa ujumla, kwamba utaratibu ambao tunatunga mambo ya kazi.
Hebu\(f(x)=2−5x\). Hebu\(g(x)=\sqrt{x}.\) Tafuta\((f∘g)(x)\).
Suluhisho
\((f∘g)(x)=2−5\sqrt{x}.\)
Fikiria kazi\(f\) na\(g\) ilivyoelezwa na
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|
| \(f(x)\) | 0 | 4 | 2 | 4 | -2 | 0 | -2 | 4 |
| \(x\) | -4 | -2 | 0 | 2 | 4 |
|---|---|---|---|---|---|
| \(g(x)\) | 1 | 0 | 3 | 0 | 5 |
- Tathmini\((g∘f)(3)\),\((g∘f)(0)\).
- Hali ya uwanja na aina mbalimbali ya\((g∘f)(x)\).
- Tathmini\((f∘f)(3)\),\((f∘f)(1)\).
- Hali ya uwanja na aina mbalimbali ya\((f∘f)(x)\).
Suluhisho:
1. \((g∘f)(3)=g(f(3))=g(−2)=0\)
\((g∘f)(0)=g(4)=5\)
2.Domain ya\(g∘f\) ni kuweka\(\{−3,−2,−1,0,1,2,3,4\}.\) Tangu mbalimbali ya\(f\) ni kuweka\(\{−2,0,2,4\},\) mbalimbali ya\(g∘f\) ni kuweka\(\{0,3,5\}.\)
3. \((f∘f)(3)=f(f(3))=f(−2)=4\)
\((f∘f)(1)=f(f(1))=f(−2)=4\)
4.Domain ya\(f∘f\) ni kuweka\(\{−3,−2,−1,0,1,2,3,4\}.\) Tangu mbalimbali ya\(f\) ni kuweka\(\{−2,0,2,4\},\) mbalimbali ya\(f∘f\) ni kuweka\(\{0,4\}.\)
Duka ni matangazo ya mauzo ya 20% off bidhaa zote. Caroline ina Coupon kwamba entitles yake ya ziada 15% off bidhaa yoyote, ikiwa ni pamoja na kuuza bidhaa. Ikiwa Caroline anaamua kununua kipengee kwa bei ya awali ya\(x\) dola, ni kiasi gani ataishia kulipa ikiwa anatumia kikapu chake kwa bei ya kuuza? Tatua tatizo hili kwa kutumia kazi ya composite.
Suluhisho
Kwa kuwa bei ya kuuza ni 20% mbali ya bei ya awali, ikiwa kipengee ni\(x\) dola, bei yake ya kuuza hutolewa na\(f(x)=0.80x\). Kwa kuwa kikapu kinampa mtu binafsi kwa asilimia 15 ya bei ya kipengee chochote, ikiwa kipengee ni\(y\) dola, bei, baada ya kutumia kikapu, hutolewa na g (y) =0.85y. Kwa hiyo, kama bei ni\(x\) dola za awali, bei yake ya kuuza itakuwa\(f(x)=0.80x\) na kisha bei yake ya mwisho baada ya kuponi itakuwa\(g(f(x))=0.85(0.80x)=0.68x\).
Ikiwa vitu vinauzwa kwa 10% ya bei yao ya awali, na mteja ana kikapu cha ziada cha 30%, itakuwa nini bei ya mwisho ya kipengee ambacho ni\(x\) dola za awali, baada ya kutumia kikapu kwa bei ya kuuza?
Kidokezo
Bei ya kuuza ya bidhaa na bei ya awali ya\(x\) dola ni\(f(x)=0.90x\). Bei ya kuponi kwa bidhaa ambayo ni\(y\) dola ni\(g(y)=0.70y\).
Suluhisho
\((g∘f)(x)=0.63x\)
Ulinganifu wa Kazi
Grafu za kazi fulani zina mali ya ulinganifu ambayo inatusaidia kuelewa kazi na sura ya grafu yake. Kwa mfano, fikiria kazi\(f(x)=x^4−2x^2−3\) iliyoonyeshwa kwenye Kielelezo\(\PageIndex{12a}\). Kama sisi kuchukua sehemu ya Curve kwamba uongo na haki ya\(y\) -axis na flip juu ya\(y\) -axis, ni kuweka hasa juu ya Curve upande wa kushoto wa\(y\) -axis. Katika kesi hii, tunasema kazi ina ulinganifu kuhusu\(y\) -axis. Kwa upande mwingine, fikiria kazi\(f(x)=x^3−4x\) iliyoonyeshwa kwenye Kielelezo\(\PageIndex{12b}\). Ikiwa tunachukua grafu na kugeuka\(180°\) juu ya asili, grafu mpya itaonekana sawa. Katika kesi hii, tunasema kazi ina ulinganifu kuhusu asili.
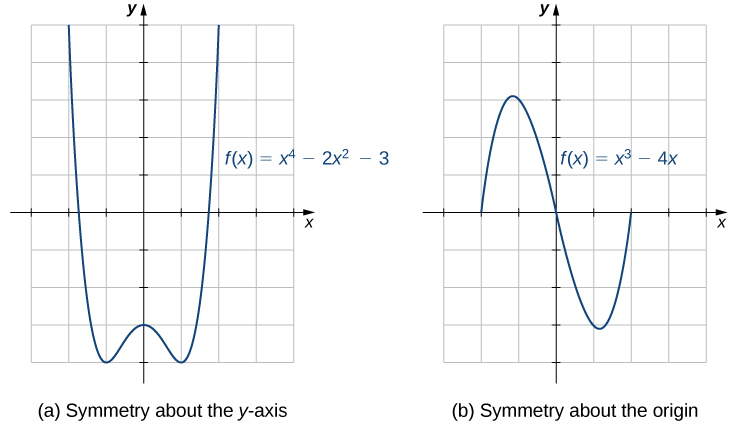
Ikiwa tunapewa grafu ya kazi, ni rahisi kuona kama grafu ina moja ya mali hizi za ulinganifu. Lakini bila grafu, tunawezaje kuamua algebraically kama kazi\(f\) ina ulinganifu? Kuangalia Kielelezo\(\PageIndex{12a}\) tena, tunaona kwamba tangu\(f\) ni symmetric kuhusu\(y\) -axis, kama uhakika\((x,y)\) ni juu ya grafu, uhakika\((−x,y)\) ni juu ya grafu. Kwa maneno mengine,\(f(−x)=f(x)\). Kama kazi\(f\) ina mali hii, tunasema\(f\) ni hata kazi, ambayo ina ulinganifu kuhusu\(y\) -axis. Kwa mfano,\(f(x)=x^2\) ni kwa sababu
\(f(−x)=(−x)^2=x^2=f(x).\)
Kwa upande mwingine, kuangalia Kielelezo\(\PageIndex{12b}\) tena, ikiwa kazi\(f\) ni ya kawaida kuhusu asili, basi wakati wowote hatua\((x,y)\) iko kwenye grafu, hatua pia\((−x,−y)\) iko kwenye grafu. Kwa maneno mengine,\(f(−x)=−f(x)\). Kama\(f\) ina mali hii, tunasema\(f\) ni kazi isiyo ya kawaida, ambayo ina ulinganifu kuhusu asili. Kwa mfano,\(f(x)=x^3\) ni isiyo ya kawaida kwa sababu
\(f(−x)=(−x)^3=−x^3=−f(x).\)
- Kama\(f(x)=f(−x)\) kwa wote\(x\) katika uwanja wa\(f\), basi\(f\) ni hata kazi. Kazi hata ni sawa kuhusu\(y\) -axis.
- Kama\(f(−x)=−f(x)\) kwa wote\(x\) katika uwanja wa\(f\), basi\(f\) ni kazi isiyo ya kawaida. Kazi isiyo ya kawaida ni ya kawaida kuhusu asili.
Kuamua kama kila moja ya kazi zifuatazo ni hata, isiyo ya kawaida, au wala.
- \(f(x)=−5x^4+7x^2−2\)
- \(f(x)=2x^5−4x+5\)
- \(f(x)=\frac{3x}{x^2+1}\)
Suluhisho
Kuamua kama kazi ni hata au isiyo ya kawaida, sisi kutathmini\(f(−x)\) na kulinganisha na\(f(x)\) na\(−f(x)\).
1. \(f(−x)=−5(−x)^4+7(−x)^2−2=−5x^4+7x^2−2=f(x).\)Kwa hiyo,\(f\) ni hata.
2. \(f(−x)=2(−x)^5−4(−x)+5=−2x^5+4x+5.\)Sasa,\(f(−x)≠f(x).\) Zaidi ya hayo, akibainisha kuwa\(−f(x)=−2x^5+4x−5\), tunaona kwamba\(f(−x)≠−f(x)\). Kwa hiyo,\(f\) ni hata wala isiyo ya kawaida.
3. \(f(−x)=3(−x)/((−x)2+1)\)\(=−3x/(x^2+1)=\)\(−[3x/(x^2+1)]=−f(x).\)Kwa hiyo,\(f\) ni isiyo ya kawaida.
Kuamua kama\(f(x)=4x^3−5x\) ni hata, isiyo ya kawaida, au wala.
- Kidokezo
-
Linganisha\(f(−x)\) na\(f(x)\) na\(−f(x)\).
- Jibu
-
\(f(x)\)ni isiyo ya kawaida.
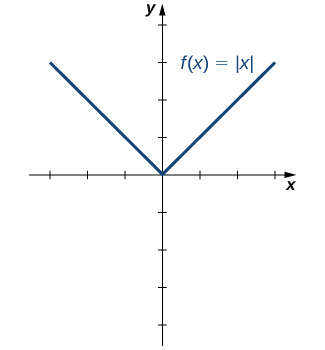
Kazi moja ya ulinganifu ambayo hutokea mara kwa mara ni thamani kamili kazi, imeandikwa kama\(|x|\). Kazi ya thamani kamili hufafanuliwa kama
\[f(x)=\begin{cases} -x, & \text{if }x<0 \\ x, & \text{if } x≥0 \end{cases} \nonumber \]
Wanafunzi wengine huelezea kazi hii kwa kusema kuwa “inafanya kila kitu chanya.” Kwa ufafanuzi wa kazi kamili ya thamani, tunaona kwamba kama\(x<0\), basi\(|x|=−x>0,\) na kama\(x>0\), basi\(|x|=x>0.\) Hata hivyo, kwa\(x=0,\)\(|x|=0.\) hiyo, ni sahihi zaidi kusema kwamba kwa pembejeo zote zisizo zero, pato ni chanya, lakini kama\(x=0\), pato\(|x|=0\). Tunahitimisha kwamba aina mbalimbali ya kazi ya thamani kamili ni\(\{y\,|\,y≥0\}.\) Katika Kielelezo\(\PageIndex{13}\), tunaona kwamba kazi ya thamani kamili ni ya ulinganifu kuhusu\(y\) -axis na kwa hiyo ni kazi hata.
Pata uwanja na aina mbalimbali za kazi\(f(x)=2|x−3|+4\).
Suluhisho
Kwa kuwa kazi ya thamani kamili inaelezwa kwa namba zote halisi, uwanja wa kazi hii ni\((−∞,∞)\). Tangu\(|x−3|≥0\) kwa wote\(x\), kazi\(f(x)=2|x−3|+4≥4\). Kwa hiyo, upeo ni, kwa zaidi, kuweka\(\{y\,|\,y≥4\}.\) Ili kuona kwamba upeo ni, kwa kweli, seti hii yote, tunahitaji kuonyesha kwamba kwa kuwa\(y≥4\) kuna idadi halisi\(x\) kama hiyo
\(2|x−3|+4=y\)
Nambari halisi\(x\) inatimiza equation hii kwa muda mrefu kama
\(|x−3|=\frac{1}{2}(y−4)\)
Tangu\(y≥4\), tunajua\(y−4≥0\), na hivyo upande wa kulia wa equation ni nonnegative, hivyo inawezekana kwamba kuna ufumbuzi. Zaidi ya hayo,
\(|x−3|=\begin{cases} −(x−3), & \text{if } x<3\\x−3, & \text{if } x≥3\end{cases}\)
Kwa hiyo, tunaona kuna ufumbuzi wawili:
\(x=±\frac{1}{2}(y−4)+3\).
Aina mbalimbali za kazi hii ni\(\{y\,|\,y≥4\}.\)
Kwa kazi\(f(x)=|x+2|−4\), tafuta kikoa na upeo.
- Kidokezo
-
\(|x+2|≥0\)kwa idadi yote halisi\(x\).
- Jibu
-
Domain =\((−∞,∞)\), mbalimbali =\(\{y\,|\,y≥−4\}.\)
Dhana muhimu
- Kazi ni ramani kutoka seti ya pembejeo kwa seti ya matokeo na pato moja hasa kwa kila pembejeo.
- Kama hakuna uwanja imesemwa kwa ajili\(y=f(x),\) ya kazi uwanja ni kuchukuliwa kuwa seti ya namba\(x\) zote halisi ambayo kazi hufafanuliwa.
- Wakati sketching grafu ya kazi\(f,\) kila mstari wima inaweza intersect grafu, mara nyingi, mara moja.
- Kazi inaweza kuwa na idadi yoyote ya zeros, lakini ina, kwa zaidi,\(y\) moja-intercept.
- Ili kufafanua muundo\(g∘f\), aina mbalimbali za\(f\) lazima ziwe katika uwanja wa\(g\).
- Hata kazi ni symmetric kuhusu\(y\) -axis ambapo kazi isiyo ya kawaida ni symmetric kuhusu asili.
Mlinganyo muhimu
- Muundo wa kazi mbili
\((g∘f)(x)=g\big(f(x)\big)\)
- Kazi kamili ya thamani
\(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)
faharasa
- kazi kamili ya thamani
- \(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)
- kazi ya composite
- kupewa kazi mbili\(f\) na\(g\), kazi mpya, ulionyehsa\(g∘f\), vile kwamba\((g∘f)(x)=g(f(x))\)
- kupungua kwa muda\(I\)
- kazi kupungua kwa muda\(I\) kama, kwa ajili ya wote\(x_1,\,x_2∈I,\;f(x_1)≥f(x_2)\) kama\(x_1<x_2\)
- tegemezi kutofautiana
- variable pato kwa ajili ya kazi
- kikoa
- seti ya pembejeo kwa ajili ya kazi
- hata kazi
- kazi ni hata kama\(f(−x)=f(x)\) kwa wote\(x\) katika uwanja wa\(f\)
- kazi
- seti ya pembejeo, seti ya matokeo, na utawala wa ramani kila pembejeo kwa pato moja
- grafu ya kazi
- seti ya pointi\((x,y)\) kama hiyo\(x\) ni katika uwanja wa\(f\) na\(y=f(x)\)
- kuongezeka kwa muda\(I\)
- kazi kuongezeka kwa muda\(I\) kama kwa ajili ya wote\(x_1,\,x_2∈I,\;f(x_1)≤f(x_2)\) kama\(x_1<x_2\)
- tofauti ya kujitegemea
- pembejeo variable kwa ajili ya kazi
- kazi isiyo ya kawaida
- kazi ni isiyo ya kawaida ikiwa\(f(−x)=−f(x)\) kwa wote\(x\) katika uwanja wa\(f\)
- mbalimbali
- seti ya matokeo kwa ajili ya kazi
- ulinganifu kuhusu asili
- grafu ya kazi\(f\) ni ya kawaida kuhusu asili ikiwa\((−x,−y)\) iko kwenye grafu ya\(f\) wakati wowote\((x,y)\) ulipo kwenye grafu
- ulinganifu kuhusu\(y\) -axis
- grafu ya kazi\(f\) ni sawa kuhusu\(y\) -axis ikiwa\((−x,y)\) iko kwenye grafu ya\(f\) wakati wowote\((x,y)\) ulipo kwenye grafu
- meza ya maadili
- meza iliyo na orodha ya pembejeo na matokeo yao yanayofanana
- mtihani wa mstari wa wima
- kutokana na grafu ya kazi, kila mstari wima intersects grafu, saa zaidi, mara moja
- zero za kazi
- wakati idadi halisi\(x\) ni sifuri ya kazi\(f,\;f(x)=0\)


