6.7: Mifano ya kielelezo na ya Logarithmic

Malengo ya kujifunza

• Mfano ukuaji wa kielelezo na kuoza.
• Tumia Sheria ya Newton ya Baridi.
• Tumia mifano ya ukuaji wa vifaa.
• Chagua mfano sahihi wa data.
• Express mfano kielelezo katika msingi\(e\).

Tayari tumechunguza baadhi ya matumizi ya msingi ya kazi za kielelezo na za logarithmic. Katika sehemu hii, tunachunguza baadhi ya maombi muhimu kwa kina zaidi, ikiwa ni pamoja na isotopu za mionzi na Sheria ya Newton ya Baridi.

Kielelezo\(\PageIndex{1}\): Reactor utafiti nyuklia ndani Neely Nuclear Kituo cha Utafiti juu ya Taasisi ya Teknolojia ya Georgia chuo (mikopo: Georgia Tech Taasisi

Mfano wa ukuaji wa Kielelezo na Kuoza

Katika maombi halisi ya ulimwengu, tunahitaji mfano tabia ya kazi. Katika mfano wa hisabati, tunachagua kazi ya kawaida ya kawaida na mali ambazo zinaonyesha kuwa itakuwa mfano wa hali halisi ya ulimwengu tunayotaka kuchambua. Katika kesi ya ukuaji wa haraka, tunaweza kuchagua kazi ya ukuaji wa kielelezo:

\[y=A_0e^{kt}\]

ambapo\(A_0\) ni sawa na thamani kwa wakati sifuri,\(e\) ni mara kwa mara Euler ya, na\(k\) ni mara kwa mara chanya ambayo huamua kiwango cha (asilimia) ya ukuaji. Tunaweza kutumia kielelezo ukuaji kazi katika maombi kuwashirikisha mara mbili wakati, wakati inachukua kwa wingi mara mbili. Matukio kama vile wakazi wa wanyamapori, uwekezaji wa kifedha, sampuli za kibiolojia, na maliasili zinaweza kuonyesha ukuaji kulingana na muda wa mara mbili. Katika baadhi ya maombi, hata hivyo, kama tutaona wakati sisi kujadili vifaa equation, mfano vifaa wakati mwingine inafaa data bora kuliko mfano kielelezo.

Kwa upande mwingine, kama wingi ni kuanguka kwa kasi kuelekea sifuri, bila milele kufikia sifuri, basi tunapaswa pengine kuchagua kielelezo kuoza mfano. Tena, tuna fomu\(y=A_0e^{kt}\) ambapo\(A_0\) ni thamani ya kuanzia, na\(e\) ni mara kwa mara Euler ya. Sasa\(k\) ni mara kwa mara hasi ambayo huamua kiwango cha kuoza. Tunaweza kutumia kielelezo kuoza mfano wakati sisi ni kuhesabu nusu ya maisha, au wakati inachukua kwa dutu kwa exponentially kuoza kwa nusu ya kiasi yake ya awali. Sisi kutumia nusu ya maisha katika maombi kuwashirikisha isotopu mionzi.

Katika uchaguzi wetu wa kazi ili kutumika kama mfano wa hisabati, mara nyingi tunatumia pointi za data zilizokusanywa na uchunguzi makini na kipimo ili kujenga pointi kwenye grafu na tumaini tunaweza kutambua sura ya grafu. Ukuaji wa kielelezo na grafu za kuoza zina sura tofauti, kama tunavyoweza kuona katika Kielelezo\(\PageIndex{2}\) na Kielelezo\(\PageIndex{3}\). Ni muhimu kukumbuka kwamba, ingawa sehemu za kila moja ya grafu mbili zinaonekana kulala juu ya\(x\) -axis, ni umbali mdogo juu ya\(x\) -axis.

Kielelezo\(\PageIndex{2}\): grafu inayoonyesha ukuaji wa kielelezo. equation ni\(y=2e^{3x}\).

Kielelezo\(\PageIndex{3}\): graph kuonyesha kuoza kielelezo. equation ni\(y=3e^{−2x}\).

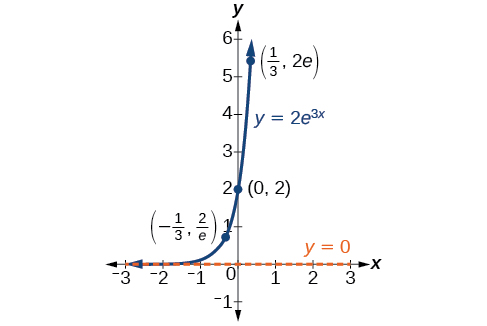
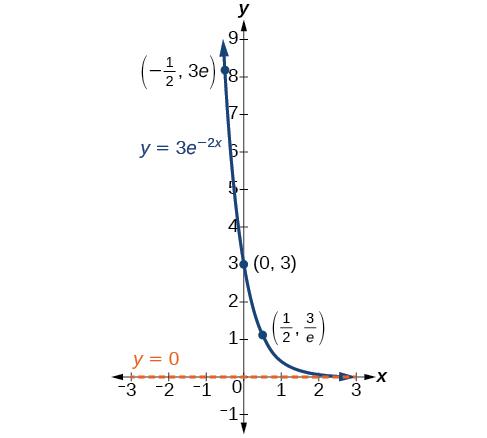
Ukuaji wa kielelezo na kuoza mara nyingi huhusisha idadi kubwa sana au ndogo sana. Ili kuelezea namba hizi, mara nyingi tunatumia amri za ukubwa. Utaratibu wa ukubwa ni nguvu ya kumi, wakati nambari inavyoelezwa kwa notation ya kisayansi, na tarakimu moja upande wa kushoto wa decimal. Kwa mfano, umbali wa nyota iliyo karibu, Proxima Centauri, iliyopimwa kwa kilomita, ni\(40,113,497,200,000\) kilomita. Imeelezwa kwa notation ya kisayansi, hii ni\(4.01134972 × 1013\). Kwa hiyo, tunaweza kuelezea nambari hii kama kuwa na utaratibu wa ukubwa\(1013\).

\(y=a_0e^{kt}\)

Kazi ya kielelezo na fomu\(y=A_0e^{kt}\) ina sifa zifuatazo:

• kazi moja kwa moja
• asymptote ya usawa:\(y=0\)
• kikoa:\((–\infty, \infty)\)
• masafa:\((0,\infty)\)
• \(x\)kukatiza: hakuna
• \(y\)-kukatiza:\((0,A_0)\)
• kuongezeka kama\(k>0\) (angalia Kielelezo\(\PageIndex{4}\))
• kupungua ikiwa\(k<0\) (angalia Kielelezo\(\PageIndex{4}\))

0 na kwa pointi zilizoandikwa (1/k, (A_0) e), (0, A_0), na (-1/k, (A_0) /e). Grafu ya pili ni ya wakati k<0 na kwa alama zilizoandikwa (-1/k, (A_0) e), (0, A_0), na (1/k, (A_0) /e)." src="https://math.libretexts.org/@api/dek.../fig_6.8.4.jpg">

Kielelezo\(\PageIndex{4}\): kielelezo kazi mifano ukuaji kielelezo wakati\(k>0\) na kielelezo kuoza wakati\(k<0\).

Mfano\(\PageIndex{1}\): Graphing Exponential Growth

Idadi ya bakteria mara mbili kila saa. Ikiwa utamaduni ulianza na\(10\) bakteria, graph idadi ya watu kama kazi ya muda.

Suluhisho

Wakati kiasi kinakua kwa asilimia fasta kwa wakati wa kitengo, ukuaji ni kielelezo. Ili kupata\(A_0\) tunatumia ukweli kwamba\(A_0\) ni kiasi wakati sifuri, hivyo\(A_0=10\). Ili kupata\(k\), tumia ukweli kwamba baada ya saa moja idadi\((t=1)\) ya watu mara mbili kutoka\(10\)\(20\) kwa.Fomu inatokana kama ifuatavyo

\[\begin{align*} 20&= 10e^{k\cdot 1}\\ 2&= e^k \qquad \text{Divide by 10}\\ \ln2&= k \qquad \text{Take the natural logarithm} \end{align*}\]

hivyo\(k=\ln(2)\). Hivyo equation tunataka grafu ni\(y=10e^{(\ln2)t}=10{(e^{\ln2})}^t=10·2^t\). Grafu inavyoonyeshwa kwenye Kielelezo\(\PageIndex{5}\).

Kielelezo\(\PageIndex{5}\): Grafu ya\(y=10e^{(\ln2)t}\)

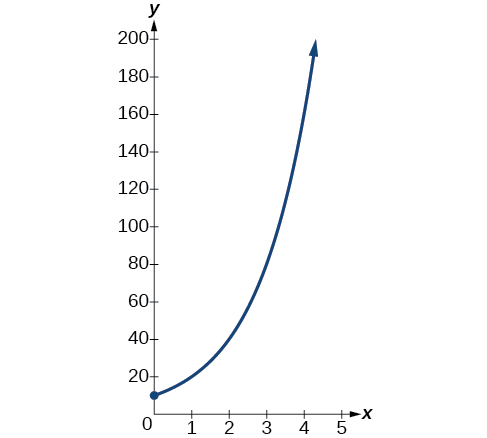
Uchambuzi

Idadi ya bakteria baada ya masaa kumi ni\(10,240\). Tunaweza kuelezea kiasi hiki ni kuwa ya utaratibu wa ukubwa\(10^4\). Idadi ya bakteria baada ya masaa ishirini ni ya utaratibu wa ukubwa\(10^7\), hivyo tunaweza kusema kwamba idadi ya watu imeongezeka kwa amri tatu za ukubwa katika masaa kumi.\(10,485,760\)

Nusu ya maisha

Sasa tunageuka kwenye kuoza kwa ufafanuzi. Moja ya maneno ya kawaida yanayohusiana na kuoza kwa kielelezo, kama ilivyoelezwa hapo juu, ni nusu ya maisha, urefu wa muda inachukua kiasi cha kuoza kwa kiasi kikubwa kupungua hadi nusu ya kiasi chake cha awali. Kila isotopi ya mionzi ina nusu ya maisha, na mchakato unaoelezea kuoza kielelezo wa isotopu huitwa kuoza kwa mionzi.

Ili kupata nusu ya maisha ya kazi inayoelezea kuoza kwa ufafanuzi, tatua usawa wafuatayo:

\(\dfrac{1}{2}A_0=A_0e^{kt}\)

Tunaona kwamba nusu ya maisha inategemea tu mara kwa mara\(k\) na si kwa kiasi cha kuanzia\(A_0\).

Fomu hiyo inatokana kama ifuatavyo:

\[\begin{align*} \dfrac{1}{2}A_0&= A_0e^{kt}\\ \dfrac{1}{2}&= e^{kt} \qquad \text{Divide by } A_0\\ \ln \left (\dfrac{1}{2} \right )&= ktv \qquad \text{Take the natural log}\\ -\ln(2)&= kt \qquad \text{Apply laws of logarithms}\\ -\ln(2)k&= t \qquad \text{Divide by k} \end{align*}\]

Tangu\(t\), wakati, ni chanya,\(k\) lazima, kama inavyotarajiwa, kuwa hasi. Hii inatupa formula nusu ya maisha

\[t=−\dfrac{\ln(2)}{k}\]

Kutokana na nusu ya maisha, pata kiwango cha kuoza.

1. Andika\(A=A_0e^{kt}\).
2. Badilisha nafasi\(A\)\(\dfrac{1}{2}A_0\) na ubadilishe\(t\) na nusu ya maisha ya kupewa.
3. Tatua kupata\(k\). \(k\)Eleza kama thamani halisi (usizunguze).

Kumbuka: Inawezekana pia kupata kiwango cha kuoza kwa kutumia\(k=−\ln(2)t\).

Mfano\(\PageIndex{2}\): Finding the Function that Describes Radioactive Decay

Nusu ya maisha ya kaboni-14 ni\(5,730\) miaka. Eleza kiasi cha kaboni-14 iliyobaki kama kazi ya muda,\(t\).

Suluhisho

Fomu hii inatokana kama ifuatavyo.

\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for } f(t)\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{ \left (\tfrac{\ln(0.5)}{5730} \right ) t} \qquad \text{Substitute for r in the continuous growth formula} \end{align*}\]

Kazi inayoelezea kuoza kwa kuendelea ni\(f(t)=A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\). Tunaona kwamba mgawo wa\(t\),\(\dfrac{\ln(0.5)}{5730}≈−1.2097×10^{−4}\) ni hasi, kama inavyotarajiwa katika kesi ya kuoza kwa maonyesho.

Zoezi\(\PageIndex{1}\)

Nusu ya maisha ya plutonium-244 ni\(80,000,000\) miaka. Kupata kazi inatoa kiasi cha kaboni-14 iliyobaki kama kazi ya muda, kipimo katika miaka.

Jibu

\(f(t)=A_0e^{−0.0000000087t}\)

Radicobon Dating

Fomu ya kuoza kwa mionzi ni muhimu katika dating radiocarbon, ambayo hutumiwa kuhesabu tarehe ya takriban mmea au mnyama alikufa. Radiocarbon dating iligunduliwa mwaka 1949 na Willard Libby, ambaye alishinda Tuzo ya Nobel kwa ugunduzi wake. Inalinganisha tofauti kati ya uwiano wa isotopi mbili za kaboni katika artifact ya kikaboni au kisukuku na uwiano wa isotopi hizo mbili hewani. Inaaminika kuwa sahihi kwa ndani kuhusu\(1\%\) makosa kwa mimea au wanyama waliokufa ndani ya\(60,000\) miaka ya mwisho.

Kaboni-14 ni isotopu ya mionzi ya kaboni ambayo ina nusumaisha ya\(5,730\) miaka. Inatokea kwa kiasi kidogo katika dioksidi kaboni katika hewa tunayopumua. Wengi wa kaboni duniani ni kaboni-12, ambayo ina uzito atomiki ya\(12\) na si mionzi. Wanasayansi wameamua uwiano wa kaboni-14 hadi kaboni-12 hewani kwa\(60,000\) miaka ya mwisho, wakitumia pete za miti na sampuli nyingine za kikaboni za tarehe zinazojulikana-ingawa uwiano umebadilika kidogo zaidi ya karne nyingi.

Mradi mmea au mnyama yupo hai, uwiano wa isotopi mbili za kaboni mwilini wake ni karibu na uwiano katika angahewa. Unapokufa, kaboni-14 katika mwili wake huharibika na haubadilishwa. Kwa kulinganisha uwiano wa kaboni-14 hadi kaboni-12 katika sampuli ya kuoza kwa uwiano unaojulikana katika angahewa, tarehe mmea au mnyama alikufa inaweza kuhesabiwa.

Kwa kuwa nusu ya maisha ya kaboni-14 ni\(5,730\) miaka, formula ya kiasi cha kaboni-14 iliyobaki baada ya\(t\) miaka ni

\(A≈A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\)

wapi

• \(A\)ni kiasi cha kaboni-14 iliyobaki
• \(A_0\)ni kiasi cha kaboni-14 wakati mmea au mnyama alianza kuoza.

Fomu hii inatokana kama ifuatavyo:

\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for f(t)}\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t} \qquad \text{Substitute for r in the continuous growth formula}\\ \end{align*}\]

Ili kupata umri wa kitu, tunatatua usawa huu kwa\(t\):

\(t=\dfrac{\ln \left (\dfrac{A}{A_0} \right )}{−0.000121}\)

Kwa umuhimu, tunapuuza hapa maelezo mengi ambayo mwanasayansi anazingatia wakati wa kufanya dating ya kaboni-14, na tunaangalia tu formula ya msingi. Uwiano wa kaboni-14 hadi kaboni-12 katika anga ni takriban\(0.0000000001%\). Hebu\(r\) uwiano wa kaboni-14 hadi kaboni-12 katika artifact hai au kisukuku kuwa tarehe, kuamua na njia inayoitwa spintillation kioevu. Kutoka equation\(A≈A_0e^{−0.000121t}\) tunajua uwiano wa asilimia ya kaboni-14 katika kitu sisi ni dating kwa asilimia ya kaboni-14 katika anga ni\(r=\dfrac{A}{A_0}≈e^{−0.000121t}\). Sisi kutatua equation hii kwa\(t\), kupata

\(t=\dfrac{\ln(r)}{−0.000121}\)

Kutokana na asilimia ya kaboni-14 katika kitu, tambua umri wake.

1. Eleza asilimia iliyotolewa ya kaboni-14 kama decimal sawa,\(k\).
2. Mbadala\(k\) kwa equation\(t=\dfrac{\ln(r)}{−0.000121}\) na kutatua kwa umri,\(t\).

Mfano\(\PageIndex{3}\): Finding the Age of a Bone

Kipande cha mfupa kinapatikana ambacho kina kaboni-14 yake\(20\%\) ya awali. Kwa mwaka wa karibu, mfupa ni umri gani?

Suluhisho

Sisi badala\(20\%=0.20\) ya\(k\) katika equation na kutatua kwa\(t\):

\[\begin{align*} t&= \dfrac{\ln(r)}{-0.000121} \qquad \text{Use the general form of the equation}\\ &= \dfrac{\ln(0.20)}{-0.000121} \qquad \text{Substitute for r}\\ &\approx 13301 \qquad \text{Round to the nearest year} \end{align*}\]

Kipande cha mfupa ni karibu\(13,301\) miaka.

Uchambuzi

Vyombo vinavyopima asilimia ya kaboni-14 ni nyeti sana na, kama tunavyotaja hapo juu, mwanasayansi atahitaji kufanya kazi nyingi zaidi kuliko tulivyofanya ili kuridhika. Hata hivyo, dating kaboni ni sahihi tu kuhusu\(1\%\), hivyo umri huu unapaswa kupewa kama\(13,301\)\(13,301\) miaka\(\pm 1\%\) au\(\pm 133\) miaka.

Zoezi\(\PageIndex{2}\)

Cesium-137 ina nusu ya maisha ya\(30\) takriban miaka. Ikiwa tunaanza na\(200\) mg ya cesium-137, itachukua zaidi au chini ya\(230\) miaka mpaka\(1\) milligram tu inabaki?

Jibu

chini ya\(230\) miaka,\(229.3157\) kuwa halisi

Kuhesabu Muda wa Mara mbili

Kwa kiasi cha kuoza, tuliamua muda gani ulichukua kwa nusu ya dutu ili kuoza. Kwa kuongezeka kwa kiasi, tunaweza kutaka kujua ni muda gani inachukua kwa wingi mara mbili. Kama tulivyosema hapo juu, wakati unachukua kwa wingi kwa mara mbili inaitwa muda wa mara mbili.

Kutokana na usawa wa msingi wa ukuaji wa kielelezo\(A=A_0e^{kt}\), wakati wa mara mbili unaweza kupatikana kwa kutatua wakati kiasi cha awali kimeongezeka mara mbili, yaani, kwa kutatua\(2A_0=A_0e^{kt}\).

Fomu hiyo inatokana kama ifuatavyo:

\[\begin{align*} 2A_0&= A_0e^{kt}\\ 2&= e^{kt} \qquad \text{Divide by } A_0\\ \ln2&= kt \qquad \text{Take the natural logarithm}\\ t& =\dfrac{\ln2}{k} \qquad \text{Divide by the coefficient of t} \end{align*}\]

Hivyo mara dufu ni

\[t=\dfrac{\ln2}{k}\]

Mfano\(\PageIndex{4}\): Finding a Function That Describes Exponential Growth

Kwa mujibu wa Sheria ya Moore, muda wa mara mbili kwa idadi ya transistors ambayo inaweza kuweka kwenye chip ya kompyuta ni takriban miaka miwili. Kutoa kazi inayoelezea tabia hii.

Suluhisho

Fomu hiyo inatokana kama ifuatavyo:

\[\begin{align*} t&= \dfrac{\ln2}{k} \qquad \text{The doubling time formula}\\ 2&= \dfrac{\ln2}{k} \qquad \text{Use a doubling time of two years}\\ k&= \dfrac{\ln2}{2} \qquad \text{Multiply by k and divide by 2}\\ A&= A_0e^{\tfrac{\ln2}{2}t} \qquad \text{Substitute k into the continuous growth formula} \end{align*}\]

Kazi ni\(A=A_0e^{\dfrac{\ln2}{2}t}\).

Zoezi\(\PageIndex{3}\)

Takwimu za hivi karibuni zinaonyesha kuwa, kama ya 2013, kiwango cha ukuaji kilichotabiriwa na Sheria ya Moore hakina tena. Ukuaji umepungua kwa muda mara mbili ya takriban miaka mitatu. Kupata kazi mpya ambayo inachukua muda tena mara mbili katika akaunti.

Jibu

\(f(t)=A_0e^{\tfrac{\ln2}{3}t}\)

Kutumia Sheria ya Newton ya Baridi

Uozo wa kielelezo unaweza pia kutumika kwa joto. Wakati kitu cha moto kinasalia katika hewa inayozunguka ambayo iko kwenye joto la chini, joto la kitu kitapungua kwa kiasi kikubwa, likiongezeka kwa kasi kama inakaribia joto la hewa linalozunguka. Kwenye grafu ya kazi ya joto, kiwango cha juu kinafanana na asymptote ya usawa kwenye joto la hewa inayozunguka. Isipokuwa joto la kawaida ni sifuri, hii itahusiana na mabadiliko ya wima ya kazi ya kuoza ya kielelezo. Tafsiri hii inaongoza kwa Sheria ya Newton ya Baridi, formula ya kisayansi kwa joto kama kazi ya muda kama joto la kitu ni sawa na joto la kawaida

\(T(t)=ae^{kt}+T_s\)

Fomu hii inatokana kama ifuatavyo:

\[\begin{align*} T(t)&= Ab^{ct}+T_s\\ T(t)&= Ae^{\ln(b^{ct})}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{ct\ln b}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{kt}+T_s \qquad \text{Rename the constant c } ln b \text{, calling it } k\\ \end{align*}\]

SHERIA YA NEWTON YA BARIDI

Joto la kitu\(T\), katika hewa inayozunguka na joto\(T_s\) litaishi kulingana na formula

\[T(t)=Ae^{kt}+T_s\]

wapi

• \(t\)ni wakati
• \(A\)ni tofauti kati ya joto la awali la kitu na mazingira
• \(k\)ni mara kwa mara, kiwango cha kuendelea ya baridi ya kitu

Kutokana na seti ya masharti, tumia Sheria ya Newton ya Baridi.

1. Weka\(T_s\) sawa na\(y\) -kuratibu ya asymptote ya usawa (kawaida joto la kawaida).
2. Badilisha maadili yaliyotolewa katika fomu ya ukuaji wa kuendelea\(T(t)=Ae^{kt}+T_s\) ili kupata vigezo\(A\) na\(k\).
3. Kubadilisha wakati uliotaka kupata joto au joto la taka ili kupata muda.

Mfano\(\PageIndex{5}\): Using Newton’s Law of Cooling

Cheesecake inachukuliwa nje ya tanuri na joto la ndani la ndani la\(165°F\), na huwekwa kwenye\(35°F\) jokofu. Baada ya\(10\) dakika, cheesecake imechochea\(150°F\). Ikiwa tunapaswa kusubiri mpaka cheesecake imechochea\(70°F\) kabla ya kula, tutasubiri muda gani?

Suluhisho

Kwa sababu jirani hewa joto katika jokofu ni\(35\) digrii, joto cheesecake kuoza exponentially kuelekea\(35\), kufuatia equation

\(T(t)=Ae^{kt}+35\)

Tunajua joto la awali lilikuwa\(165\), hivyo\(T(0)=165\).

\[\begin{align*} 165&= Ae^{k0}+35 \qquad \text{Substitute } (0,165)\\ A&= 130 \qquad \text{Solve for A} \end{align*}\]

Tulipewa hatua nyingine ya data\(T(10)=150\), ambayo tunaweza kutumia kutatua\(k\).

\[\begin{align*} 150&= 130e^{k10}+35 \qquad \text{Substitute } (10, 150)\\ 115&= 130e^{k10} \qquad \text{Subtract 35}\\ \dfrac{115}{130}&= e^{10k} \qquad \text{Divide by 130}\\ \ln\left (\dfrac{115}{130} \right )&= 10k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln \left (\dfrac{115}{130} \right )}{10}\\ &= -0.0123 \qquad \text{Divide by the coefficient of k} \end{align*}\]

Hii inatupa equation kwa ajili ya baridi ya cheesecake:\(T(t)=130e^{–0.0123t}+35\).

Sasa tunaweza kutatua kwa muda itachukua kwa joto ili baridi kwa\(70\) digrii.

\[\begin{align*} 70&= 130e^{-0.0123t}+35 \qquad \text{Substitute in 70 for } T(t)\\ 35&= 130e^{-0.0123t} \qquad \text{Subtract 35}\\ \dfrac{35}{130}&= e^{-0.0123t} \qquad \text{Divide by 130}\\ \ln \left (\dfrac{35}{130} \right )&= -0.0123t \qquad \text{Take the natural log of both sides}\\ t&= \dfrac{\ln \left (\dfrac{35}{130} \right )}{-0.0123}\\ &\approx 106.68 \qquad \text{Divide by the coefficient of t} \end{align*}\]

Itachukua\(107\) muda wa dakika, au saa moja na\(47\) dakika, kwa cheesecake ili kupendeza\(70°F\).

Zoezi\(\PageIndex{4}\)

Mtungi wa maji katika\(40\) digrii Fahrenheit huwekwa kwenye chumba\(70\) cha shahada. Saa moja baadaye, joto limeongezeka hadi\(45\) digrii. Itachukua muda gani kwa joto kuongezeka kwa\(60\) digrii?

Jibu

\(6.026\)masaa

Kutumia Mifano ya ukuaji wa vifaa

Ukuaji wa kielelezo hauwezi kuendelea milele. Mifano ya kielelezo, wakati inaweza kuwa na manufaa kwa muda mfupi, huwa na kuanguka mbali tena wanaendelea. Fikiria mwandishi anayetaka ambaye anaandika mstari mmoja siku moja na anapanga mara mbili idadi ya mistari anayoandika kila siku kwa mwezi. Mwishoni mwa mwezi, lazima aandike mistari zaidi ya\(17\) bilioni, au kurasa moja ya nusu bilioni. Haiwezekani, ikiwa haiwezekani, kwa mtu yeyote kuandika kiasi hicho kwa muda mfupi. Hatimaye, mfano wa kielelezo lazima uanze kufikia thamani fulani ya kikwazo, na kisha ukuaji unalazimika kupungua. Kwa sababu hii, mara nyingi ni bora kutumia mfano na kufungwa juu badala ya mfano wa ukuaji wa kielelezo, ingawa mfano wa ukuaji wa kielelezo bado ni muhimu kwa muda mfupi, kabla ya kufikia thamani ya kikwazo.

Mfano wa ukuaji wa vifaa ni takriban kielelezo mwanzoni, lakini ina kiwango cha kupungua kwa ukuaji kama pato linakaribia kifungo cha juu cha mfano, kinachoitwa uwezo wa kubeba. Kwa mara kwa mara\(a\),\(b\), na\(c\), ukuaji wa vifaa ya idadi ya watu baada ya muda\(x\) inawakilishwa na mfano

\(f(x)=\dfrac{c}{1+ae^{−bx}}\)

Grafu katika Kielelezo\(\PageIndex{6}\) inaonyesha jinsi kiwango cha ukuaji kinabadilika kwa muda. Grafu huongezeka kutoka kushoto kwenda kulia, lakini kiwango cha ukuaji kinaongezeka tu mpaka kufikia kiwango chake cha ukuaji wa kiwango cha juu, wakati ambapo kiwango cha ongezeko kinapungua.

Kielelezo\(\PageIndex{6}\)

UKUAJI WA VIFAA

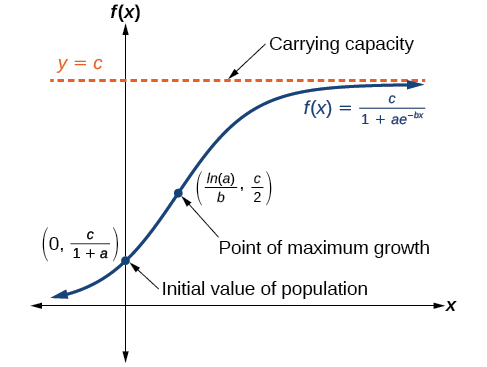
Mtindo wa ukuaji wa vifaa ni

\[f(x)=\dfrac{c}{1+ae^{−bx}}\]

wapi

• \(\dfrac{c}{1+a}\)ni thamani ya awali
• \(c\)ni uwezo wa kubeba, au thamani ya kupunguza
• \(b\)ni mara kwa mara kuamua na kiwango cha ukuaji wa uchumi.

Mfano\(\PageIndex{6}\): Using the Logistic-Growth Model

Janga la mafua huenea kwa njia ya idadi ya watu kwa kasi, kwa kiwango kinachotegemea mambo mawili: Watu wengi ambao wana homa, huenea kwa kasi zaidi, na pia watu wengi wasioambukizwa huko, huenea kwa kasi zaidi. Sababu hizi mbili hufanya mfano wa vifaa kuwa nzuri kujifunza kuenea kwa magonjwa ya kuambukiza. Na, kwa wazi, kuna thamani ya juu kwa idadi ya watu walioambukizwa: idadi ya watu wote.

Kwa mfano, wakati\(t=0\) kuna mtu mmoja katika jamii ya\(1,000\) watu ambao wana homa. Kwa hiyo, katika jamii hiyo,\(1,000\) watu wengi wanaweza kuwa na homa. Watafiti wanaona kwamba kwa aina hii hasa ya homa, vifaa ukuaji wa mara kwa mara ni\(b=0.6030\). Tathmini ya idadi ya watu katika jamii hii ambao watakuwa na homa hii baada ya siku kumi. Kutabiri jinsi watu wengi katika jamii hii kuwa na homa hii baada ya muda mrefu kupita.

Suluhisho

Sisi badala ya data iliyotolewa katika mfano wa ukuaji wa vifaa

\(f(x)=\dfrac{c}{1+ae^{−bx}}\)

Kwa sababu kwa\(1,000\) watu wengi, idadi ya watu wote wa jamii, wanaweza kupata homa, tunajua thamani kikwazo ni\(c=1000\). Ili kupata\(a\), tunatumia formula ambayo idadi ya kesi kwa wakati\(t=0\) ni\(\dfrac{c}{1+a}=1\), ambayo inafuata\(a=999\) kwamba.Mfano huu unatabiri kwamba, baada ya siku kumi, idadi ya watu ambao wamekuwa na homa ni\(f(x)=\dfrac{1000}{1+999e^{−0.6030x}}≈293.8\). Kwa sababu idadi halisi lazima idadi nzima (mtu ana ama alikuwa na homa au la) sisi pande zote kwa\(294\). Kwa muda mrefu, idadi ya watu ambao watakabiliana na homa ni thamani ya kupunguza,\(c=1000\).

Uchambuzi

Kumbuka kwamba, kwa sababu tunashughulika na virusi, hatuwezi kutabiri kwa uhakika idadi ya watu walioambukizwa. Mfano huo unakaribia tu idadi ya watu walioambukizwa na hautatupa maadili halisi au halisi.

Grafu katika Kielelezo\(\PageIndex{7}\) inatoa picha nzuri ya jinsi mtindo huu inafaa data.

Kielelezo\(\PageIndex{7}\): Grafu ya\(f(x)=\dfrac{1000}{1+999e^{−0.6030x}}\)

Zoezi\(\PageIndex{5}\)

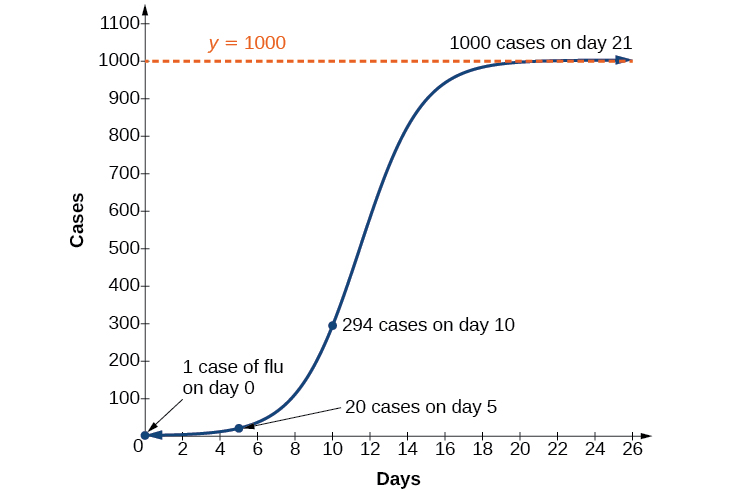
Kutumia mfano katika Mfano hapo juu, tathmini idadi ya matukio ya homa ya siku\(15\).

Jibu

\(895\)kesi juu ya siku\(15\)

Kuchagua Mfano sahihi wa Data

Sasa kwa kuwa tumejadili mifano mbalimbali ya hisabati, tunahitaji kujifunza jinsi ya kuchagua mfano sahihi kwa data ghafi tunayo. Sababu nyingi huathiri uchaguzi wa mfano wa hisabati, kati ya ambayo ni uzoefu, sheria za kisayansi, na mifumo katika data yenyewe. Sio data zote zinaweza kuelezewa na kazi za msingi. Wakati mwingine, kazi imechaguliwa ambayo inakaribia data juu ya muda uliopewa. Kwa mfano, tuseme data zilikusanywa juu ya idadi ya nyumba kununuliwa nchini Marekani kutoka miaka 1960 hadi 2013. Baada ya kupanga njama hizi katika njama ya kutawanya, tunaona kwamba sura ya data kutoka miaka 2000 hadi 2013 hufuata safu ya logarithmic. Tunaweza kuzuia muda kutoka 2000 hadi 2010, tumia uchambuzi wa kurudi nyuma kwa kutumia mfano wa logarithmic, na uitumie kutabiri idadi ya wanunuzi wa nyumba kwa mwaka 2015.

Aina tatu za kazi ambazo mara nyingi zinafaa katika mifano ya hisabati ni kazi za mstari, kazi za kielelezo, na kazi za logarithmic. Ikiwa data iko kwenye mstari wa moja kwa moja, au inaonekana kusema uongo karibu na mstari wa moja kwa moja, mfano wa mstari unaweza kuwa bora. Ikiwa data ni isiyo ya mstari, mara nyingi tunazingatia mfano wa kielelezo au logarithmic, ingawa mifano mingine, kama mifano ya quadratic, inaweza pia kuchukuliwa.

Katika kuchagua kati ya mfano wa kielelezo na mfano wa logarithmic, tunaangalia jinsi data inavyozunguka. Hii inaitwa concavity. Kama sisi kuteka mstari kati ya pointi mbili data, na wote (au zaidi) ya data kati ya pointi hizo mbili uongo juu ya mstari huo, tunasema Curve ni concave chini. Tunaweza kufikiria kama bakuli linalopungua chini na hivyo hawezi kushikilia maji. Kama wote (au zaidi) ya data kati ya pointi hizo mbili uongo chini ya mstari, tunasema Curve ni concave up. Katika kesi hii, tunaweza kufikiria bakuli ambayo hupanda juu na kwa hiyo inaweza kushikilia maji. Curve kielelezo, kama kupanda au kuanguka, kama inawakilisha ukuaji au kuoza, daima concave mbali na asymptote yake usawa. Curve ya logarithmic daima ni concave mbali na asymptote yake ya wima. Katika kesi ya data chanya, ambayo ni kesi ya kawaida, curve exponential daima concave up, na Curve logarithmic daima concave chini.

Curve vifaa mabadiliko concavity. Inaanza concave up na kisha mabadiliko ya concave chini ya hatua fulani, inayoitwa hatua ya inflection.

Baada ya kutumia grafu ili kutusaidia kuchagua aina ya kazi ya kutumia kama mfano, tunabadilisha pointi, na kutatua kupata vigezo. Tunapunguza hitilafu ya pande zote kwa kuchagua pointi mbali mbali iwezekanavyo.

Mfano\(\PageIndex{7}\): Choosing a Mathematical Model

Je, mfano wa mstari, wa kielelezo, wa logarithmic, au wa vifaa unaofaa zaidi maadili yaliyoorodheshwa katika Jedwali\(\PageIndex{1}\)? Pata mfano, na utumie grafu ili uangalie uchaguzi wako.

Jedwali\(\PageIndex{1}\)

\(x\)	1	2	3	4	5	6	7	8	9
\(y\)	0	1.386	2.197	2.773	3.219	3.584	3.892	4.159	4.394

Suluhisho

Kwanza, fanya data kwenye grafu kama kwenye Mchoro\(\PageIndex{8}\). Kwa madhumuni ya kuchora picha, pande zote data kwa tarakimu mbili muhimu.

Kielelezo\(\PageIndex{8}\)

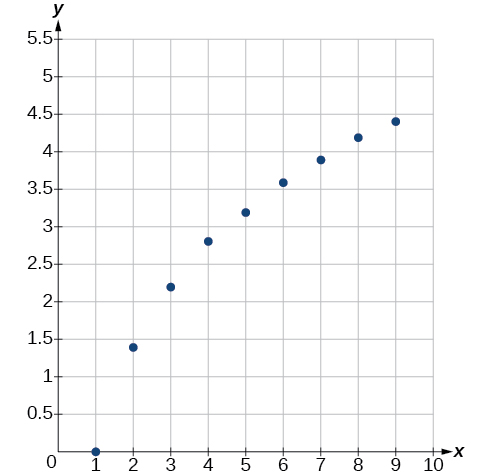
Kwa wazi, pointi hazilala kwenye mstari wa moja kwa moja, kwa hiyo tunakataa mfano wa mstari. Kama sisi kuteka mstari kati ya mbili yoyote ya pointi, zaidi au yote ya pointi kati ya pointi hizo mbili uongo juu ya mstari, hivyo graph ni concave chini, na kupendekeza mfano logarithmic. Tunaweza kujaribu\(y=a\ln(bx)\). Kuziba katika hatua ya kwanza,\((1,0)\), anatoa\(0=a\ln b\). Tunakataa kesi hiyo\(a=0\) (ikiwa ni, matokeo yote yatakuwa\(0\)), kwa hiyo tunajua\(\ln(b)=0\). Hivyo\(b=1\) na\(y=a\ln(x)\). Halafu tunaweza kutumia hatua ya\((9,4.394)\) kutatua kwa\(a\):

\[\begin{align*} y&= a\ln(x)\\ 4.394&= a\ln(9)\\ a&= \dfrac{4.394}{\ln(9)} \end{align*}\]

Kwa sababu\(a=\dfrac{4.394}{\ln(9)}≈2\), mfano sahihi kwa data ni\(y=2\ln(x)\).

Kuangalia usahihi wa mfano, sisi grafu kazi pamoja na pointi zilizotolewa kama katika Kielelezo\(\PageIndex{9}\).

Kielelezo\(\PageIndex{9}\): grafu ya\(y=2\ln x\).

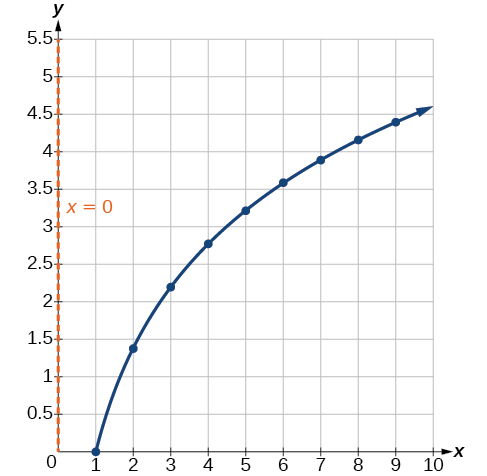
Tunaweza kuhitimisha kuwa mfano huo ni sawa na data.

Linganisha Kielelezo\(\PageIndex{9}\) kwenye grafu ya\(y=\ln(x^2)\) inavyoonekana kwenye Kielelezo\(\PageIndex{10}\).

Kielelezo\(\PageIndex{10}\): Grafu ya\(y=\ln(x^2)\)

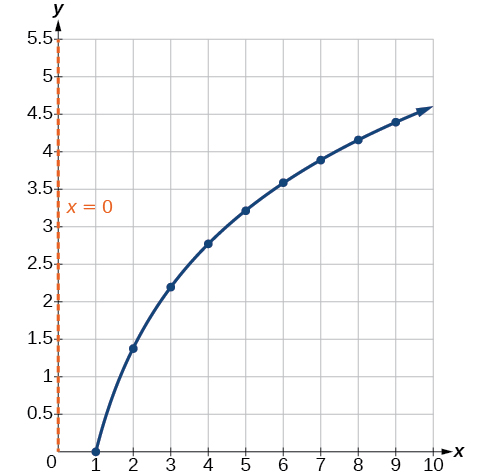
Grafu zinaonekana kuwa sawa wakati\(x>0\). Cheti cha haraka kinathibitisha hitimisho hili:\(y=\ln(x^2)=2\ln(x)\) kwa\(x>0\).

Hata hivyo, kama\(x<0\), grafu ya\(y=\ln(x^2)\) ni pamoja na “ziada” tawi, kama inavyoonekana katika Kielelezo\(\PageIndex{11}\). Hii hutokea kwa sababu, wakati\(y=2\ln(x)\) hauwezi kuwa na maadili hasi katika kikoa (kama maadili hayo yangeweza kulazimisha hoja kuwa hasi), kazi\(y=\ln(x^2)\) inaweza kuwa na maadili hasi ya kikoa.

Kielelezo\(\PageIndex{11}\)

Zoezi\(\PageIndex{6}\)

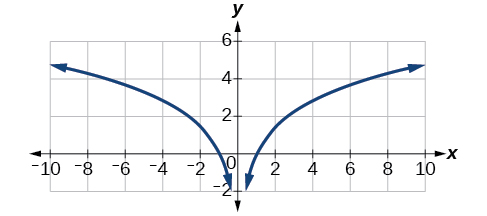
Je, mfano wa mstari, wa kielelezo, au wa logarithmic unafaa zaidi data katika Jedwali\(\PageIndex{2}\)? Pata mfano.

Jedwali\(\PageIndex{2}\)

\(x\)	1	2	3	4	5	6	7	8	9
\(y\)	3.297	5.437	8.963	14.778	24.365	40.172	66.231	109.196	180.034

Jibu

Kielelezo\(y=2e^{0.5x}\).

Kuonyesha Mfano wa Kielelezo katika Msingi\(e\)

Wakati nguvu na logarithms ya msingi wowote inaweza kutumika katika mfano, besi mbili za kawaida ni\(10\) na\(e\). Katika sayansi na hisabati, msingi mara nyingi\(e\) hupendekezwa. Tunaweza kutumia sheria za exponents na sheria za logarithms kubadili msingi wowote kwa msingi\(e\).

Kutokana na mfano na fomu\(y=ab^x\), change it to the form \(y=A_0e^{kx}\).

1. Andika upya\(y=ab^x\) kama\(y=ae^{\ln(b^x)}\).
2. Tumia utawala wa nguvu wa logarithms kuandika upya\(y\) kama\(y=ae^{x\ln(b)}=ae^{\ln{(b)}^x}\).
3. Kumbuka kwamba\(a=A_0\) na\(k=\ln(b)\) katika equation\(y=A_0e^{kx}\).

Mfano\(\PageIndex{8}\): Changing to base \(e\)

Badilisha kazi\(y=2.5{(3.1)}^x\) ili kazi hii hiyo imeandikwa kwa fomu\(y=A_0e^{kx}\).

Suluhisho

Fomu hiyo inatokana kama ifuatavyo:

\[\begin{align*} y&= 2.5{(3.1)}^x\\ &= 2.5e^{\ln({3.1}^x)} \qquad \text{Insert exponential and its inverse}\\ &= 2.5e^{x\ln3.1} \qquad \text{Laws of logs}\\ &= 2.5e^{(\ln3.1)x} \qquad \text{Commutative law of multiplication} \end{align*}\]

Zoezi\(\PageIndex{7}\)

Mabadiliko ya kazi\(y=3{(0.5)}^x\) kwa moja kuwa\(e\) kama msingi.

Jibu

\(y=3e^{(\ln0.5)x}\)

vyombo vya habari

Fikia rasilimali hizi za mtandaoni kwa maelekezo ya ziada na mazoezi na mifano ya kielelezo na ya logarithmic.

• Maombi ya Logarithm — pH
• Mfano wa kielelezo - Umri Kutumia Nusu
• Sheria ya Newton ya Baridi
• Kielelezo ukuaji Kutokana Mara dufu Muda
• Ukuaji wa Kielelezo - Pata Kiasi cha awali kilichopewa Muda

Mlinganyo muhimu

Fomu ya nusu ya maisha	Ikiwa\(A=A_0e^{kt}\)\(k<0\), nusu ya maisha ni\(t=−\dfrac{\ln(2)}{k}\).
Carbon-14 dating	\(t=\dfrac{\ln(\dfrac{A}{A_0})}{−0.000121}\). \(A_0\)\(A\)ni kiasi cha kaboni-14 wakati mmea au mnyama alikufa \(t\) ni kiasi cha kaboni-14 iliyobaki leo ni umri wa kisukuku katika miaka
Mara dufu wakati formula	Kama\(A=A_0e^{kt}\),\(k>0\), mara dufu ni\(t=\dfrac{\ln2}{k}\)
Sheria ya Newton ya Baridi	\(T(t)=Ae^{kt}+T_s\),\(T_s\) wapi joto la kawaida\(A=T(0)−T_s\), na\(k\) ni kiwango cha kuendelea cha baridi.

Dhana muhimu

• Kazi ya msingi ya kielelezo ni\(f(x)=ab^x\). Kama\(b>1\), tuna ukuaji kielelezo; kama\(0<b<1\), tuna kielelezo kuoza.
• Tunaweza pia kuandika formula hii katika suala la ukuaji wa kuendelea kama\(A=A_0e^{kx}\),\(A_0\) wapi thamani ya kuanzia. Kama\(A_0\) ni chanya, basi tuna ukuaji kielelezo wakati\(k>0\) na kielelezo kuoza wakati\(k<0\). Angalia Mfano\(\PageIndex{1}\).
• Kwa ujumla, sisi kutatua matatizo yanayohusisha ukuaji wa kielelezo au kuoza katika hatua mbili. Kwanza, tunaanzisha mfano na kutumia mfano ili kupata vigezo. Kisha tunatumia formula na vigezo hivi kutabiri ukuaji na kuoza. Angalia Mfano\(\PageIndex{2}\).
• Tunaweza kupata umri,\(t\), ya artifact hai kwa kupima kiasi\(k\), ya kaboni-14 iliyobaki katika artifact na kutumia formula ya\(t=\dfrac{\ln(k)}{−0.000121}\) kutatua kwa\(t\). Angalia Mfano\(\PageIndex{3}\).
• Kutokana na dutu ya mara mbili wakati au nusu ya muda, tunaweza kupata kazi ambayo inawakilisha ukuaji wake kielelezo au kuoza. Angalia Mfano\(\PageIndex{4}\).
• Tunaweza kutumia Sheria ya Newton ya Baridi ili kupata muda gani itachukua kwa kitu kilichopozwa ili kufikia joto linalohitajika, au kupata joto gani kitu kitakavyokuwa baada ya muda fulani. Angalia Mfano\(\PageIndex{5}\).
• Tunaweza kutumia kazi za ukuaji wa vifaa ili kutengeneza hali halisi ya ulimwengu ambapo kiwango cha ukuaji kinabadilika kwa muda, kama vile ukuaji wa idadi ya watu, kuenea kwa magonjwa, na kuenea kwa uvumi. Angalia Mfano\(\PageIndex{6}\).
• Tunaweza kutumia data halisi ya ulimwengu iliyokusanywa baada ya muda ili kuchunguza mwenendo. Ujuzi wa grafu linear, kielelezo, logarithmic, na vifaa hutusaidia kuendeleza mifano inayofaa zaidi data zetu. Angalia Mfano\(\PageIndex{7}\).
• Kazi yoyote kielelezo na fomu\(y=abx\) inaweza kuandikwa upya kama kazi sawa kielelezo na fomu\(y=A_0e^{kx}\) ambapo\(k=\ln b\). Angalia Mfano\(\PageIndex{8}\).