11.4: Uhifadhi wa kasi ya Angular

Malengo ya kujifunza

• Tumia uhifadhi wa kasi ya angular ili kuamua kasi ya angular ya mfumo unaozunguka ambapo wakati wa inertia unabadilika
• Eleza jinsi nishati ya kinetic ya mzunguko inavyobadilika wakati mfumo unapobadilika katika wakati wote wa inertia na kasi ya angular

Hadi sasa, tumeangalia kasi ya angular ya mifumo yenye chembe za uhakika na miili imara. Sisi pia kuchambuliwa torques kushiriki, kwa kutumia usemi kwamba inahusiana nje wavu moment na mabadiliko katika kasi angular. Mifano ya mifumo inayoitii equation hii ni pamoja na tairi ya baiskeli inayozunguka kwa uhuru ambayo hupungua kwa muda kutokana na moment inayotokana na msuguano, au kupunguza kasi ya mzunguko wa Dunia juu ya mamilioni ya miaka kutokana na vikosi vya msuguano vinavyotumika kwenye uharibifu wa mawimbi.

Hata hivyo, tuseme hakuna wakati wa nje wa nje kwenye mfumo,\(\sum \vec{\tau}\) = 0. Katika kesi hii, tunaweza kuanzisha sheria ya uhifadhi wa kasi ya angular.

Sheria ya Uhifadhi wa kasi ya Angular

Kasi ya angular ya mfumo wa chembe karibu na hatua katika sura ya kumbukumbu ya inertial iliyohifadhiwa huhifadhiwa ikiwa hakuna moment ya nje ya nje karibu na hatua hiyo:

\[\frac{d \vec{L}}{dt} = 0 \label{11.10}\]

au

\[\vec{L} = \vec{l}_{1} + \vec{l}_{2} + \cdots + \vec{l}_{N} = constant \ldotp \label{11.11}\]

Kumbuka kuwa kasi ya jumla ya angular\(\vec{L}\) imehifadhiwa. Yoyote ya momenta ya angular ya mtu binafsi inaweza kubadilika kwa muda mrefu kama jumla yao inabakia mara kwa mara. Sheria hii ni sawa na kasi ya mstari inayohifadhiwa wakati nguvu ya nje kwenye mfumo ni sifuri.

Kama mfano wa uhifadhi wa kasi angular, Kielelezo\(\PageIndex{1}\) inaonyesha skater barafu kutekeleza spin. Wakati wa wavu juu yake ni karibu sana na sifuri kwa sababu kuna msuguano mdogo kati ya skates zake na barafu. Pia, msuguano unafanywa karibu sana na hatua ya pivot. Wote\(|\vec{F}|\) na\(|\vec{r}|\) ni ndogo, hivyo\(|\vec{\tau}|\) ni duni. Kwa hiyo, anaweza kuzunguka kwa muda mrefu. Anaweza pia kuongeza kiwango chake cha spin kwa kuvuta mikono na miguu yake. Kwa nini kuunganisha mikono na miguu yake kwa kuongeza kiwango chake cha spin? Jibu ni kwamba kasi yake ya angular ni mara kwa mara, ili

\[L' = L\]

au

\[I' \omega' = I \omega,\]

ambapo kiasi primed rejea hali baada ya yeye kujiondoa katika mikono yake na kupunguza muda wake wa hali. Kwa sababu mimi ni ndogo, kasi ya angular lazima\(\omega\) iongeze ili kuweka kasi ya angular mara kwa mara.

Kielelezo\(\PageIndex{1}\): (a) Skater ya barafu inazunguka juu ya ncha ya skate yake na mikono yake kupanuliwa. Mwendo wake wa angular huhifadhiwa kwa sababu wakati wa wavu juu yake ni mdogo sana. (b) Kiwango chake cha spin kinaongezeka sana wakati yeye huvuta mikononi mwake, kupungua wakati wake wa inertia. Kazi anayofanya ili kuvuta mikono yake husababisha ongezeko la nishati ya kinetic ya mzunguko.

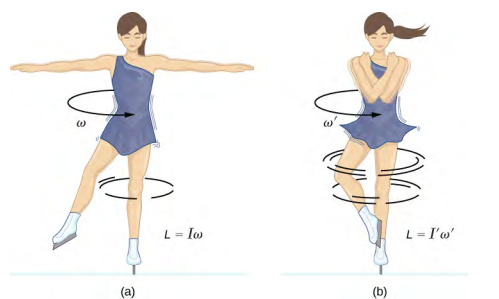
Inashangaza kuona jinsi nishati ya kinetic ya mzunguko wa skater inabadilika wakati yeye huvuta mikono yake. Nishati yake ya awali ya mzunguko ni

\[K_{Rot} = \frac{1}{2} I \omega^{2},\]

ambapo nishati yake ya mwisho ya mzunguko ni

\[K'_{Rot} = \frac{1}{2} I (\omega')^{2} \ldotp\]

Tangu\(\omega\) mimi = mimi\(\omega\), tunaweza\(\omega\) kubadilisha na kupata

\[K'_{Rot} = \frac{1}{2} I' (\omega')^{2} = \frac{1}{2} I' \left(\dfrac{I}{I'} \omega \right)^{2} = \frac{1}{2} I \omega^{2} \left(\dfrac{I}{I'}\right) = K_{Rot} \left(\dfrac{I}{I'}\right) \ldotp\]

Kwa sababu wakati wake wa inertia umepungua\(I′ < I\), nishati yake ya mwisho ya mzunguko wa kinetic imeongezeka. Chanzo cha nishati hii ya ziada ya mzunguko wa kinetic ni kazi inayohitajika kuvuta mikono yake ndani. Kumbuka kwamba silaha za skater haziingii kwenye mduara kamilifu-zinazunguka ndani. Kazi hii husababisha ongezeko la nishati ya kinetic ya mzunguko, wakati kasi yake ya angular inabakia mara kwa mara. Kwa kuwa yeye yuko katika mazingira yasiyo na msuguano, hakuna nishati inayoepuka mfumo. Hivyo, kama angeweza kupanua mikono yake kwa nafasi zao za awali, angeweza kugeuka kwa kasi yake ya awali ya angular na nishati yake ya kinetic ingeweza kurudi kwa thamani yake ya awali.

Mfumo wa jua ni mfano mwingine wa jinsi uhifadhi wa kasi wa angular unavyofanya kazi katika ulimwengu wetu. Mfumo wetu wa jua ulizaliwa kutokana na wingu kubwa la gesi na vumbi ambalo awali lilikuwa na nishati ya mzunguko. Majeshi ya mvuto yalisababisha wingu kuwa mkataba, na kiwango cha mzunguko kiliongezeka kama matokeo ya uhifadhi wa kasi ya angular (Kielelezo\(\PageIndex{2}\)).

Kielelezo\(\PageIndex{2}\): Mfumo wa jua uliunganishwa kutoka kwa wingu la gesi na vumbi ambalo lilikuwa linapokezana awali. Mzunguko wa orbital na spins ya sayari ni katika mwelekeo sawa na spin ya awali na kuhifadhi kasi ya angular ya wingu mzazi. (mikopo: mabadiliko ya kazi na NASA)

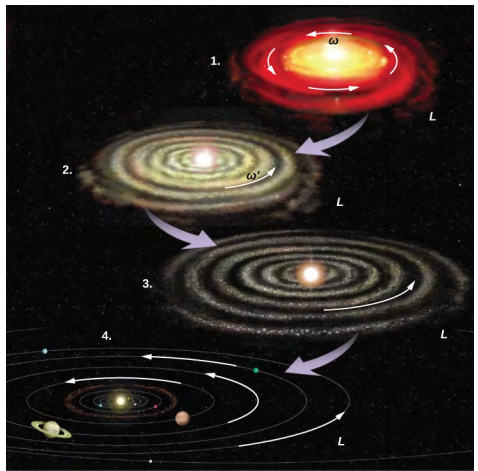
Tunaendelea majadiliano yetu na mfano ambao una maombi ya uhandisi.

Mfano\(\PageIndex{1}\): Coupled Flywheels

Flywheel huzunguka bila msuguano kwa kasi ya angular\(\omega_{0}\) = 600 rev/min kwenye shimoni isiyo na msuguano, wima ya inertia isiyo na maana ya mzunguko. Flywheel ya pili, ambayo inapumzika na ina muda wa inertia mara tatu ile ya flywheel inayozunguka, imeshuka juu yake (Kielelezo\(\PageIndex{3}\)). Kwa sababu msuguano upo kati ya nyuso, flywheels haraka sana kufikia kasi sawa ya mzunguko, baada ya hapo wao spin pamoja.

1. Tumia sheria ya uhifadhi wa kasi ya angular ili kuamua kasi\(\omega\) ya angular ya mchanganyiko.
2. Ni sehemu gani ya nishati ya awali ya kinetic inapotea katika kuunganisha kwa flywheels?

Kielelezo\(\PageIndex{3}\): Flywheels mbili ni pamoja na mzunguko pamoja.

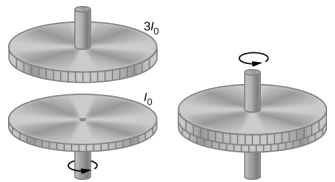
Mkakati

Sehemu (a) ni moja kwa moja kutatua kasi ya angular ya mfumo wa pamoja. Tunatumia matokeo ya (a) kulinganisha nguvu za awali na za mwisho za kinetic za mfumo kwa sehemu (b).

Suluhisho

1. Hakuna torques nje kutenda juu ya mfumo. Nguvu kutokana na msuguano hutoa wakati wa ndani, ambao hauathiri kasi ya angular ya mfumo. Kwa hiyo uhifadhi wa kasi angular inatoa\[I_{0} \omega_{0} = (I_{0} + 3I_{0}) \omega, \nonumber\]\[\omega = \frac{1}{4} \omega_{0} = 150\; rev/min = 15.7\; rad/s \ldotp \nonumber\]
2. Kabla ya kuwasiliana, flywheel moja tu inazunguka. Nishati ya kinetic ya mzunguko wa flywheel hii ni nishati ya awali ya mzunguko wa kinetic ya mfumo,\(\frac{1}{2} I_{0} \omega_{0}^{2}\). Nishati ya mwisho ya kinetic ni\[\frac{1}{2} (4I_{0}) \omega^{2} = \frac{1}{2} (4I_{0}) \left(\dfrac{\omega_{0}}{4}\right)^{2} = \frac{1}{8} I_{0} \omega_{0}^{2}. \nonumber\] Kwa hiyo, uwiano wa nishati ya mwisho ya kinetic kwa nishati ya awali ya kinetic ni\[\frac{\frac{1}{8} I_{0} \omega_{0}^{2}}{\frac{1}{2} I_{0} \omega_{0}^{2}} = \frac{1}{4} \ldotp \nonumber\] Hivyo, 3/4 ya nishati ya awali ya kinetic inapotea kwa kuunganisha kwa flywheels mbili.

Umuhimu

Tangu hali ya mzunguko ya mfumo iliongezeka, kasi ya angular ilipungua, kama inavyotarajiwa kutoka kwa sheria ya uhifadhi wa kasi ya angular. Katika mfano huu, tunaona kwamba nishati ya mwisho ya kinetic ya mfumo imepungua, kama nishati inapotea kwa kuunganisha kwa flywheels. Linganisha hii kwa mfano wa skater katika Kielelezo\(\PageIndex{1}\) kufanya kazi ya kuleta mikono yake ndani na kuongeza rotational kinetic nishati.

Zoezi\(\PageIndex{1}\)

Furaha ya kwenda pande zote kwenye uwanja wa michezo inazunguka saa 4.0 rev/min. Watoto watatu wanaruka na kuongeza wakati wa inertia ya mfumo wa merry-go-pande zote/watoto kupokezana kwa 25%. Kiwango cha mzunguko mpya ni nini?

Mfano\(\PageIndex{2A}\): Dismount from a High Bar

Gymnast ya kilo 80.0-kg hupungua kutoka kwenye bar ya juu. Anaanza kupasuka kwa ugani kamili, kisha tucks kukamilisha idadi ya mapinduzi kabla ya kutua. Muda wake wa inertia wakati kupanuliwa kikamilifu unaweza kuhesabiwa kama fimbo ya urefu 1.8 m na wakati katika tuck fimbo ya nusu urefu huo. Ikiwa kiwango chake cha mzunguko katika ugani kamili ni 1.0 rev/s na anaingia tuck wakati kituo chake cha wingi ni urefu wa 3.0 m kusonga kwa usawa kwenye sakafu, ngapi mapinduzi anaweza kutekeleza ikiwa anatoka kwenye tuck kwa urefu wa 1.8 m? Angalia Kielelezo\(\PageIndex{4}\).

Kielelezo\(\PageIndex{4}\): Gymnast hupungua kutoka kwenye bar ya juu na hufanya mapinduzi kadhaa katika nafasi iliyopangwa kabla ya kutua sawa.

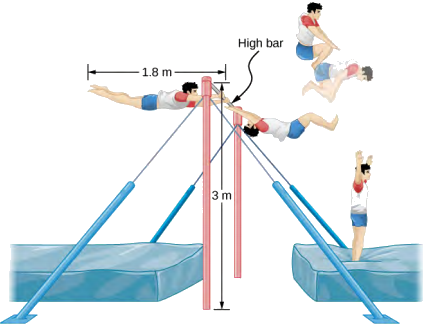
Mkakati

Kutumia uhifadhi wa kasi ya angular, tunaweza kupata kiwango cha mzunguko wake wakati wa tuck. Kutumia equations ya kinematics, tunaweza kupata muda wa muda kutoka urefu wa 3.0 m hadi 1.8 m Kwa kuwa anahamia kwa usawa kwa heshima na ardhi, usawa wa kuanguka kwa bure kurahisisha. Hii itawawezesha idadi ya mapinduzi ambayo yanaweza kutekelezwa ili kuhesabiwa. Kwa kuwa tunatumia uwiano, tunaweza kuweka vitengo kama rev/s na hatuhitaji kubadilisha kuwa radians/s.

Suluhisho

Wakati wa inertia katika ugani kamili ni\[I_{0} = \frac{1}{12} mL^{2} = \frac{1}{12} (80.0\; kg)(1.8\; m)^{2} = 21.6\; kg\; \cdotp m^{2} \ldotp \nonumber\]

Wakati wa inertia katika tuck ni\[I_{f} = \frac{1}{12} mL_{f}^{2} = \frac{1}{12} (80.0\; kg)(0.9\; m)^{2} = 5.4\; kg\; \cdotp m^{2} \ldotp \nonumber\]

Uhifadhi wa kasi ya angular:\[I_{f} \omega_{f} = I_{0} \omega_{0} \Rightarrow \omega_{f} = \frac{I_{0} \omega_{0}}{I_{f}} = \frac{(21.6\; kg\; \cdotp m^{2})(1.0\; rev/s)}{5.4\; kg\; \cdotp m^{2}} = 4.0\; rev/s \ldotp \nonumber\]

Muda wa muda katika tuck:\[t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(3.0 - 1.8) m}{9.8\; m/s}} = 0.5\; s \ldotp \nonumber\]

Katika 0.5 s, atakuwa na uwezo wa kutekeleza mapinduzi mawili saa 4.0 rev/s.

Umuhimu

Kumbuka kwamba idadi ya mapinduzi anaweza kukamilisha itategemea muda gani yeye ni hewa. Katika tatizo, yeye anaondoka bar ya juu kwa usawa chini. Aliweza pia kuondoka kwa pembe kwa heshima na ardhi, kumpa muda zaidi au chini katika hewa kulingana na angle, chanya au hasi, kwa heshima na ardhi. Gymnasts lazima kuzingatia hili wakati wao ni kutekeleza dismounts yao.

Mfano\(\PageIndex{2B}\): Conservation of Angular Momentum of a Collision

Risasi ya molekuli m = 2.0 g inahamia kwa usawa na kasi ya 500.0 m/s. risasi mgomo na inakuwa iliyoingia katika makali ya disk imara ya molekuli M = 3.2 kg na Radius R = 0.5 m.Silinda ni bure kuzunguka karibu mhimili wake na ni awali katika mapumziko (Kielelezo\(\PageIndex{5}\)). Je! Ni kasi gani ya angular ya disk mara baada ya risasi kuingizwa?

Kielelezo\(\PageIndex{5}\): risasi ni fired usawa na inakuwa iliyoingia katika makali ya disk kwamba ni bure kwa mzunguko kuhusu mhimili wake wima.

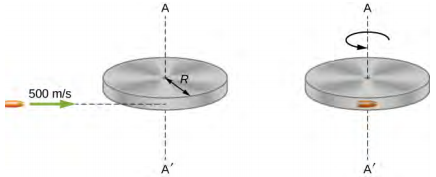
Mkakati

Kwa mfumo wa risasi na silinda, hakuna wakati wa nje unaofanya kando ya mhimili wima kupitia katikati ya diski. Hivyo, kasi ya angular pamoja na mhimili huu imehifadhiwa. Kasi ya awali ya angular ya risasi ni mVr, ambayo inachukuliwa kuhusu mhimili wa mzunguko wa disk wakati kabla ya mgongano. Kasi ya awali ya angular ya silinda ni sifuri. Hivyo, kasi ya angular ya mfumo ni mVr. Kwa kuwa kasi ya angular imehifadhiwa, kasi ya awali ya angular ya mfumo ni sawa na kasi ya angular ya risasi iliyoingia kwenye diski mara baada ya athari.

Suluhisho

Kasi ya awali ya angular ya mfumo ni

\[L_{i} = mvR \ldotp \nonumber\]

Wakati wa inertia ya mfumo na risasi iliyoingia kwenye diski ni

\[I = mR^{2} + \frac{1}{2} MR^{2} = \left(m + \dfrac{M}{2}\right) R^{2} \ldotp \nonumber\]

Mwisho wa angular kasi ya mfumo ni

\[L_{f} = I \omega_{f} \ldotp \nonumber\]

Hivyo, kwa uhifadhi wa kasi ya angular, L _i = L _f na

\[mvR = \left(m + \dfrac{M}{2}\right) R^{2} \omega_{f} \ldotp \nonumber\]

Kutatua kwa\(\omega_{f}\),

\[\omega_{f} = \frac{mvR}{\left(m + \dfrac{M}{2}\right) R^{2}} = \frac{(2.0 \times 10^{-3}\; kg)(500.0\; m/s)}{(2.0 \times 10^{-3}\; kg + 1.6\; kg)(0.50\; m)} = 1.2\; rad/s \ldotp \nonumber\]

Umuhimu

Mfumo huu unajumuisha chembe zote mbili na mwili mgumu. Uangalizi lazima uchukuliwe wakati wa kuunda kasi ya angular kabla na baada ya mgongano. Kabla ya athari kasi ya angular ya risasi inachukuliwa kuhusu mhimili wa mzunguko wa disk.