10.6: Kuhesabu Wakati wa Inertia

Malengo ya kujifunza

• Tumia wakati wa inertia kwa miili iliyofanana, imara
• Tumia theorem ya mhimili sambamba ili kupata wakati wa inertia kuhusu mhimili wowote unaofanana na moja tayari inayojulikana.
• Tumia wakati wa inertia kwa vitu vya kiwanja

Katika kifungu kilichotangulia, tulifafanua wakati wa inertia lakini haukuonyesha jinsi ya kuhesabu. Katika kifungu hiki, tunaonyesha jinsi ya kuhesabu wakati wa hali kwa aina kadhaa za vitu, pamoja na jinsi ya kutumia wakati unaojulikana wa hali ili kupata wakati wa inertia kwa mhimili uliobadilishwa au kwa kitu cha kiwanja. Sehemu hii ni muhimu sana kwa kuona jinsi ya kutumia equation ya jumla kwa vitu tata (ujuzi ambao ni muhimu kwa kozi ya juu zaidi ya fizikia na uhandisi).

Muda wa Inertia

Sisi defined wakati wa hali mimi ya kitu kuwa

\[I = \sum_{i} m_i r_i^2 \]

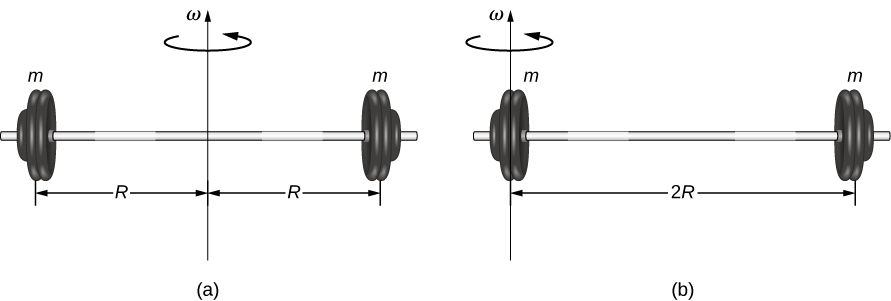
kwa raia wote uhakika kwamba kufanya juu ya kitu. Kwa sababu\(r\) ni umbali wa mhimili wa mzunguko kutoka kila kipande cha wingi ambacho hufanya kitu, wakati wa inertia kwa kitu chochote inategemea mhimili uliochaguliwa. Ili kuona hili, hebu tuchukue mfano rahisi wa raia wawili mwishoni mwa fimbo isiyo na maana (ndogo ndogo) fimbo (Kielelezo\(\PageIndex{1}\)) na uhesabu wakati wa inertia kuhusu shoka mbili tofauti. Katika kesi hiyo, summation juu ya raia ni rahisi kwa sababu raia mbili mwishoni mwa barbell zinaweza kuhesabiwa kama raia wa uhakika, na jumla hiyo ina masharti mawili tu.

Katika kesi na mhimili katikati ya barbell, kila moja ya raia mbili m ni umbali\(R\) mbali na mhimili, kutoa muda wa inertia ya

\[I_{1} = mR^{2} + mR^{2} = 2mR^{2} \ldotp\]

Katika kesi na mhimili mwishoni mwa barbell-kupita kupitia moja ya moleku-wakati wa inertia ni

\[I_{2} = m(0)^{2} + m(2R)^{2} = 4mR^{2} \ldotp\]

Kutokana na matokeo haya, tunaweza kuhitimisha kuwa ni mara mbili ngumu kugeuza barbell kuhusu mwisho kuliko kuhusu kituo chake.

Kielelezo\(\PageIndex{1}\): (a) Barbell yenye mhimili wa mzunguko kupitia kituo chake; (b) barbell yenye mhimili wa mzunguko kupitia mwisho mmoja.

Katika mfano huu, tulikuwa na raia mbili za uhakika na jumla ilikuwa rahisi kuhesabu. Hata hivyo, ili kukabiliana na vitu ambavyo si kama uhakika, tunahitaji kufikiria kwa makini kuhusu kila moja ya maneno katika equation. Equation inatuuliza jumla juu ya kila 'kipande cha moleku' umbali fulani kutoka mhimili wa mzunguko. Lakini ni nini hasa kila 'kipande cha moleku' inamaanisha nini? Kumbuka kwamba katika derivation yetu ya equation hii, kila kipande cha wingi alikuwa na ukubwa sawa wa kasi, ambayo ina maana kipande nzima alikuwa na umbali moja r kwa mhimili wa mzunguko. Hata hivyo, hii haiwezekani isipokuwa sisi kuchukua kipande infinitesimally ndogo ya molekuli dm, kama inavyoonekana katika Kielelezo\(\PageIndex{2}\).

Kielelezo\(\PageIndex{2}\): Kutumia kipande kidogo cha molekuli ili kuhesabu mchango kwa muda wa jumla wa hali.

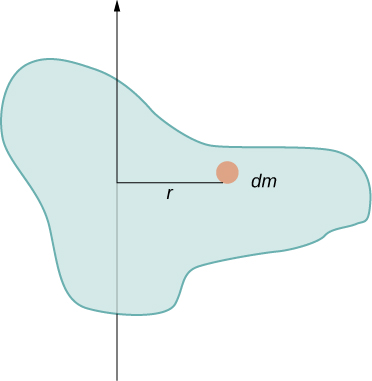
Mahitaji ya kutumia kipande kidogo cha dm ya molekuli inaonyesha kwamba tunaweza kuandika wakati wa hali kwa kutathmini muhimu juu ya raia usio na maana badala ya kufanya kiasi kikubwa juu ya raia wa mwisho:

\[I = \sum_{i} m_{i} r_{i}^{2}\]

inakuwa

\[I = \int r^{2} dm \ldotp \label{10.19}\]

Hii, kwa kweli, ni fomu tunahitaji kuzalisha equation kwa maumbo tata. Ni bora kufanya mifano maalum kwa undani ili kujisikia jinsi ya kuhesabu wakati wa inertia kwa maumbo maalum. Hii ni lengo la sehemu nyingi za sehemu hii.

Fimbo nyembamba sare na mhimili kupitia katikati

Fikiria sare (wiani na sura) fimbo nyembamba ya molekuli M na urefu L kama inavyoonekana katika Kielelezo\(\PageIndex{3}\). Tunataka fimbo nyembamba ili tuweze kudhani eneo la msalaba wa fimbo ni ndogo na fimbo inaweza kufikiriwa kama kamba ya raia kwenye mstari mmoja wa moja kwa moja. Katika mfano huu, mhimili wa mzunguko ni perpendicular kwa fimbo na hupita kupitia midpoint kwa unyenyekevu. Kazi yetu ni kuhesabu wakati wa inertia kuhusu mhimili huu. Sisi kuelekeza axes ili z-axis ni mhimili wa mzunguko na x-axis hupita kupitia urefu wa fimbo, kama inavyoonekana katika takwimu. Hii ni chaguo rahisi kwa sababu tunaweza kuunganisha kando ya x-axis.

Kielelezo\(\PageIndex{3}\): Kuhesabu wakati wa inertia mimi kwa fimbo nyembamba sare kuhusu mhimili kupitia katikati ya fimbo.

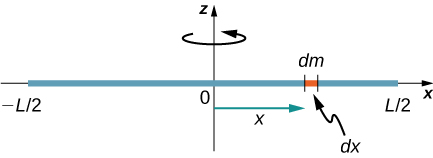
Tunafafanua dm kuwa kipengele kidogo cha molekuli inayofanya fimbo. Wakati wa inertia muhimu ni muhimu juu ya usambazaji wa wingi. Hata hivyo, tunajua jinsi ya kuunganisha juu ya nafasi, si zaidi ya wingi. Kwa hiyo tunahitaji kutafuta njia ya kuhusisha wingi kwa vigezo anga. Tunafanya hivyo kwa kutumia wiani wa mstari\(\lambda\) wa kitu, ambacho ni wingi kwa urefu wa kitengo. Tangu wiani wingi wa kitu hiki ni sare, tunaweza kuandika

\[\lambda = \frac{m}{l}\; or\; m = \lambda l \ldotp\]

Ikiwa tunachukua tofauti ya kila upande wa equation hii, tunaona

\[dm = d(\lambda l) = \lambda (dl)\]

tangu\(\lambda\) ni mara kwa mara. Tulichagua kuelekeza fimbo pamoja na mhimili wa x-kwa urahisi-hii ndio ambapo uchaguzi huo unakuwa na manufaa sana. Kumbuka kwamba kipande cha fimbo dl iko kabisa pamoja na x-axis na ina urefu dx; kwa kweli, dl = dx katika hali hii. Kwa hiyo tunaweza kuandika dm =\(\lambda\) (dx), kutupa variable ushirikiano kwamba tunajua jinsi ya kukabiliana na. Umbali wa kila kipande cha molekuli dm kutoka kwa mhimili hutolewa na x variable, kama inavyoonekana katika takwimu. Kuweka hii yote pamoja, tunapata

\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]

Hatua ya mwisho ni kuwa makini kuhusu mipaka yetu ya ushirikiano. Fimbo inaenea kutoka x =\(− \frac{L}{2}\) hadi x =\(\frac{L}{2}\), tangu mhimili iko katikati ya fimbo saa x = 0. Hii inatupa

\[\begin{split} I & = \int_{- \frac{L}{2}}^{\frac{L}{2}} x^{2} \lambda dx = \lambda \frac{x^{3}}{3} \Bigg|_{- \frac{L}{2}}^{\frac{L}{2}} \\ & = \lambda \left(\dfrac{1}{3}\right) \Bigg[ \left(\dfrac{L}{2}\right)^{3} - \left(- \dfrac{L}{2}\right)^{3} \Bigg] = \lambda \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) \\ & = \frac{1}{12} ML^{2} \ldotp \end{split}\]

Kisha, tunahesabu wakati wa inertia kwa fimbo moja nyembamba ya sare lakini kwa uchaguzi tofauti wa mhimili ili tuweze kulinganisha matokeo. Tunatarajia wakati wa hali kuwa ndogo kuhusu mhimili kupitia katikati ya molekuli kuliko mhimili wa mwisho, kama ilivyokuwa kwa mfano wa barbell mwanzoni mwa sehemu hii. Hii hutokea kwa sababu molekuli zaidi inasambazwa mbali na mhimili wa mzunguko.

Fimbo nyembamba ya Sare na Axis Mwishoni

Sasa fikiria fimbo nyembamba ya sare ya wingi\(M\) na urefu\(L\), lakini wakati huu tunahamisha mhimili wa mzunguko hadi mwisho wa fimbo. Tunataka kupata wakati wa inertia kuhusu mhimili huu mpya (Kielelezo\(\PageIndex{4}\)).

Kielelezo\(\PageIndex{4}\): Kuhesabu wakati wa inertia\(I\) kwa fimbo nyembamba sare kuhusu mhimili kupitia mwisho wa fimbo.

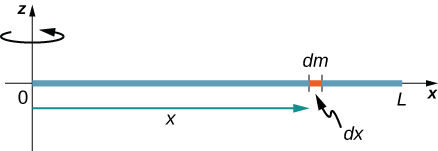
Kiasi\(dm\) kinafafanuliwa tena kuwa elementi ndogo ya molekuli inayofanya fimbo. Tu kama kabla, sisi kupata

\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]

Hata hivyo, wakati huu tuna mipaka tofauti ya ushirikiano. Fimbo inaenea kutoka\(x = 0\) kwa\(x = L\), tangu mhimili ni mwisho wa fimbo saa\(x = 0\). Kwa hiyo tunapata

\[\begin{align} I & = \int_{0}^{L} x^{2} \lambda\, dx \\[4pt] &= \lambda \frac{x^{3}}{3} \Bigg|_{0}^{L} \\[4pt] &=\lambda \left(\dfrac{1}{3}\right) \Big[(L)^{3} - (0)^{3} \Big] \\[4pt] & = \lambda \left(\dfrac{1}{3}\right) L^{3} = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) L^{3} \\[4pt] &= \frac{1}{3} ML^{2} \ldotp \label{ThinRod} \end{align} \]

Kumbuka hali ya mzunguko wa fimbo kuhusu mwisho wake ni kubwa kuliko inertia ya mzunguko kuhusu kituo chake (kulingana na mfano wa barbell) kwa sababu ya nne.

Theorem ya Sambamba ya Axis

Kufanana kati ya mchakato wa kutafuta wakati wa inertia ya fimbo kuhusu mhimili kupitia katikati yake na juu ya mhimili kupitia mwisho wake ni kushangaza, na inaonyesha kuwa kunaweza kuwa njia rahisi ya kuamua wakati wa inertia kwa fimbo kuhusu mhimili wowote sambamba na mhimili kupitia katikati ya molekuli. Mhimili huo huitwa mhimili sambamba. Kuna theorem kwa hili, inayoitwa theorem ya sambamba-axis, ambayo tunasema hapa lakini haipatikani katika maandishi haya.

Theorem ya Sambamba ya Mhimili

Hebu m kuwa wingi wa kitu na basi d kuwa umbali kutoka mhimili kupitia kituo cha kitu ya wingi kwa mhimili mpya. Kisha tuna

\[I_{\text{parallel-axis}} = I_{\text{center of mass}} + md^{2} \ldotp \label{10.20}\]

Hebu kuomba hii kwa sare fimbo nyembamba na mhimili mfano kutatuliwa hapo juu:

\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = \frac{1}{12} mL^{2} + m \left(\dfrac{L}{2}\right)^{2} = \left(\dfrac{1}{12} + \dfrac{1}{4}\right) mL^{2} = \frac{1}{3} mL^{2} \ldotp\]

Matokeo haya yanakubaliana na hesabu yetu ndefu zaidi (Equation\ ref {ThinRod}). Equation\ ref {10.20} ni equation muhimu kwamba sisi kuomba katika baadhi ya mifano na matatizo.

Zoezi\(\PageIndex{1}\)

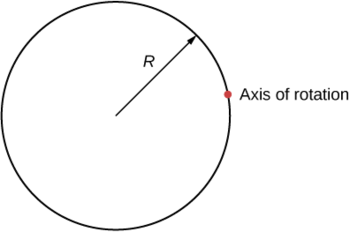
Ni wakati gani wa inertia ya silinda ya radius\(R\) na wingi\(m\) kuhusu mhimili kupitia hatua juu ya uso, kama inavyoonekana hapa chini?

Jibu

\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]

Disk Thin Uniform kuhusu Axis kupitia Kituo

Kuunganisha ili kupata wakati wa hali ya kitu mbili-dimensional ni kidogo trickier, lakini sura moja ni kawaida kufanyika katika ngazi hii ya utafiti-sare nyembamba disk kuhusu mhimili kupitia kituo chake (Kielelezo\(\PageIndex{5}\)).

Kielelezo\(\PageIndex{5}\): Kuhesabu wakati wa inertia kwa diski nyembamba kuhusu mhimili kupitia kituo chake.

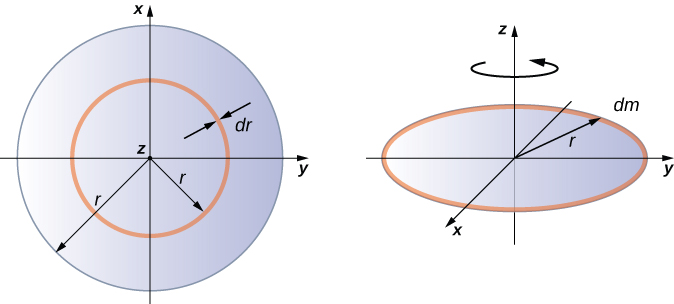
Kwa kuwa disk ni nyembamba, tunaweza kuchukua wingi kama kusambazwa kabisa katika xy-ndege. Tunaanza tena na uhusiano wa wiani wa wingi wa uso, ambayo ni wingi kwa eneo la uso wa kitengo. Kwa kuwa ni sare, wiani wa wingi wa uso\(\sigma\) ni mara kwa mara:

\[\sigma = \frac{m}{A}\]au\[\sigma A = m\] hivyo\[dm = \sigma (dA)\]

Sasa tunatumia kurahisisha eneo hilo. Eneo hilo linaweza kufikiriwa kama linajumuisha mfululizo wa pete nyembamba, ambapo kila pete ni ongezeko la wingi dm ya radius\(r\) equidistant kutoka mhimili, kama inavyoonekana katika sehemu (b) ya takwimu. Eneo la infinitesimal la kila pete\(dA\) hutolewa kwa urefu wa kila pete (\(2 \pi r\)) mara upana usio wa kawaida wa kila pete\(dr\):

\[A = \pi r^{2},\; dA = d(\pi r^{2}) = \pi dr^{2} = 2 \pi rdr \ldotp\]

Eneo kamili la diski linaundwa na kuongeza pete zote nyembamba na aina ya radius kutoka\(0\) hadi\(R\). Hii mbalimbali Radius kisha inakuwa mipaka yetu ya ushirikiano kwa\(dr\), yaani, sisi kuunganisha kutoka\(r = 0\) kwa\(r = R\). Kuweka hii yote pamoja, tuna

\[\begin{split} I & = \int_{0}^{R} r^{2} \sigma (2 \pi r) dr = 2 \pi \sigma \int_{0}^{R} r^{3} dr = 2 \pi \sigma \frac{r^{4}}{4} \Big|_{0}^{R} \\ & = 2 \pi \sigma \left(\dfrac{R^{4}}{4} - 0 \right) = 2 \pi \left(\dfrac{m}{A}\right) \left(\dfrac{R^{4}}{4}\right) = 2 \pi \left(\dfrac{m}{\pi R^{2}}\right) \left(\dfrac{R^{4}}{4}\right) = \frac{1}{2} mR^{2} \ldotp \end{split}\]

Kumbuka kuwa hii inakubaliana na thamani iliyotolewa katika Kielelezo 10.5.4.

Kuhesabu Muda wa Inertia kwa Vitu vya Kiwanja

Sasa fikiria kitu kiwanja kama vile katika Kielelezo\(\PageIndex{6}\), ambayo inaonyesha disk nyembamba mwishoni mwa fimbo nyembamba. Hii haiwezi kuunganishwa kwa urahisi ili kupata wakati wa hali kwa sababu si kitu kilichoumbwa kwa usawa. Hata hivyo, ikiwa tunarudi kwenye ufafanuzi wa awali wa wakati wa inertia kama summation, tunaweza kusababisha kwamba wakati wa kiwanja wa kitu cha inertia unaweza kupatikana kutoka kwa jumla ya kila sehemu ya kitu:

\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]

Ni muhimu kutambua kwamba wakati wa inertia ya vitu katika Equation\(\PageIndex{6}\) ni kuhusu mhimili wa kawaida. Katika kesi ya kitu hiki, hiyo itakuwa fimbo ya urefu L inayozunguka juu ya mwisho wake, na disk nyembamba ya radius\(R\) inayozunguka juu ya mhimili ulioondolewa katikati kwa umbali\(L + R\), wapi\(R\) radius ya disk. Hebu tufafanue wingi wa fimbo kuwa m _r na wingi wa disk kuwa\(m_d\).

Kielelezo\(\PageIndex{6}\): Kitu cha kiwanja kilicho na diski mwishoni mwa fimbo. Mhimili wa mzunguko iko\(A\).

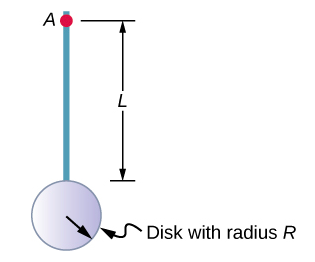
Wakati wa inertia ya fimbo ni rahisi\(\frac{1}{3} m_rL^2\), lakini tunapaswa kutumia theorem ya sambamba ya mhimili ili kupata wakati wa inertia ya disk kuhusu mhimili ulioonyeshwa. Wakati wa inertia ya disk kuhusu kituo chake ni\(\frac{1}{2} m_dR^2\) na tunatumia theorem ya sambamba ya mhimili (Equation\ ref {10.20}) ili kupata

\[I_{parallel-axis} = \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]

Kuongeza wakati wa inertia ya fimbo pamoja na wakati wa inertia ya disk na mzunguko uliobadilishwa, tunaona wakati wa inertia kwa kitu cha kiwanja kuwa

\[I_{total} = \frac{1}{3} m_{r} L^{2} + \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]

Kutumia wakati wa mahesabu ya inertia kutatua matatizo

Sasa hebu tuchunguze baadhi ya matumizi ya vitendo ya wakati wa mahesabu ya inertia.

Mfano\(\PageIndex{1}\): Person on a Merry-Go-Round

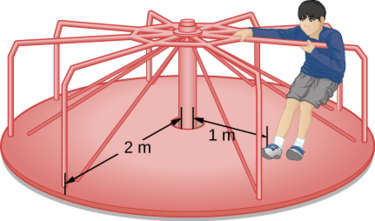
Mtoto mwenye kilo 25 anasimama\(r = 1.0\, m\) mbali na mhimili wa merry-go-round inayozunguka (Kielelezo\(\PageIndex{7}\)). Furaha ya pande zote inaweza kuhesabiwa kama disk imara ya sare yenye uzito wa kilo 500 na radius ya 2.0 m Pata wakati wa hali ya mfumo huu.

Kielelezo\(\PageIndex{7}\): Kuhesabu wakati wa inertia kwa mtoto juu ya merry-kwenda pande zote.

Mkakati

Tatizo hili linahusisha hesabu ya wakati wa inertia. Tunapewa wingi na umbali wa mhimili wa mzunguko wa mtoto pamoja na wingi na radius ya merry-go-round. Kwa kuwa ukubwa na ukubwa wa mtoto ni ndogo sana kuliko merry-kwenda pande zote, tunaweza kumkaribia mtoto kama molekuli ya uhakika. Nukuu tunayotumia ni m _c = 25 kg, r _c = 1.0 m, _m = 500 kg, r _{m = 2.0 m} Lengo letu ni kupata\(I_{total} = \sum_{i} I_{i}\) (Equation\ ref {10.21}).

Suluhisho

Kwa mtoto,\(I_c = m_cr^2\), na kwa ajili ya furaha-kwenda-pande zote,\(I_m = \frac{1}{2}m_m r^2\). Kwa hiyo

\[I_{total} = 25(1)^{2} + \frac{1}{2} (500)(2)^{2} = 25 + 1000 = 1025\; kg\; \cdotp m^{2} \ldotp \nonumber \]

Umuhimu

Thamani inapaswa kuwa karibu na wakati wa inertia ya merry-kwenda pande zote yenyewe kwa sababu ina wingi zaidi kusambazwa mbali na mhimili kuliko mtoto anavyofanya.

Mfano\(\PageIndex{2}\): Rod and Solid Sphere

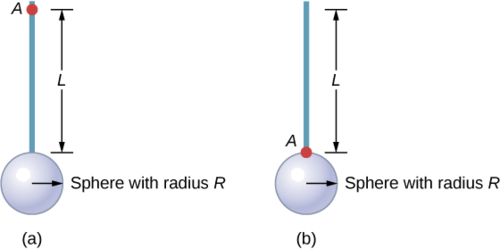
Kupata wakati wa hali ya fimbo na imara nyanja mchanganyiko kuhusu shoka mbili kama inavyoonekana hapa chini. Fimbo ina urefu wa 0.5 m na uzito wa kilo 2.0. Radi ya nyanja ni 20.0 cm na ina uzito wa kilo 1.0.

Mkakati

Kwa kuwa tuna kitu cha kiwanja katika matukio yote mawili, tunaweza kutumia theorem ya sambamba ya mhimili ili kupata wakati wa inertia kuhusu kila mhimili. Katika (a), katikati ya wingi wa nyanja iko umbali\(L + R\) kutoka kwa mhimili wa mzunguko. Katika (b), katikati ya wingi wa nyanja iko umbali\(R\) kutoka kwa mhimili wa mzunguko. Katika matukio hayo yote, wakati wa inertia ya fimbo ni kuhusu mhimili mwisho mmoja. Rejea Jedwali 10.4 kwa wakati wa inertia kwa vitu vya mtu binafsi.

a.

\[\begin{split} I_{total} & = \sum_{i} I_{i} = I_{Rod} + I_{Sphere}; \\ I_{Sphere} & = I_{center\; of\; mass} + m_{Sphere} (L + R)^{2} = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = \frac{1}{3} (20\; kg)(0.5\; m)^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.5\; m + 0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.490)\; kg\; \cdotp m^{2} = 0.673\; kg\; \cdotp m^{2} \ldotp \end{split}\]

b.

\[\begin{split} I_{Sphere} & = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} R^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.04)\; kg\; \cdotp m^{2} = 0.223\; kg\; \cdotp m^{2} \ldotp \end{split}\]

Umuhimu

Kutumia theorem ya sambamba ya mhimili hupunguza hesabu ya wakati wa inertia ya vitu vya kiwanja. Tunaona kwamba wakati wa inertia ni mkubwa zaidi katika (a) kuliko (b). Hii ni kwa sababu mhimili wa mzunguko ni karibu na katikati ya wingi wa mfumo katika (b). Mfano rahisi ni ule wa fimbo. Wakati wa inertia kuhusu mwisho mmoja ni\(\frac{1}{3}\) mL ², lakini wakati wa inertia kupitia katikati ya wingi pamoja na urefu wake ni\(\frac{1}{12}\) mL ².

Mfano\(\PageIndex{3}\): Angular Velocity of a Pendulum

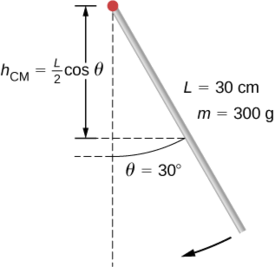
Pendulum katika sura ya fimbo (Kielelezo\(\PageIndex{8}\)) hutolewa kutoka kupumzika kwa pembe ya 30°. Ina urefu wa cm 30 na uzito 300 g.Kasi yake ya angular ni nini katika hatua yake ya chini kabisa?

Kielelezo\(\PageIndex{8}\): Pendulum katika mfumo wa fimbo hutolewa kutoka kupumzika kwa angle ya 30°.

Mkakati

Tumia uhifadhi wa nishati ili kutatua tatizo. Wakati wa kutolewa, pendulum ina nguvu ya nguvu ya mvuto, ambayo imedhamiriwa kutoka urefu wa katikati ya wingi juu ya hatua yake ya chini kabisa katika swing. Chini ya swing, nishati yote ya uwezo wa mvuto inabadilishwa kuwa nishati ya kinetic ya mzunguko.

Suluhisho

Mabadiliko katika nishati ya uwezo ni sawa na mabadiliko katika nishati ya kinetic ya mzunguko,\(\Delta U + \Delta K = 0\).

Juu ya swing:

\[U = mgh_{cm} = mgL^2 (\cos \theta). \nonumber \]

Chini ya swing,

\[U = mg \frac{L}{2}. \nonumber\]

Juu ya swing, nishati ya kinetic ya mzunguko ni K = 0. Chini ya swing, K =\(\frac{1}{2} I \omega^{2}\). Kwa hiyo:

\[\Delta U + \Delta K = 0 \Rightarrow (mg \frac{L}{2} (1 - \cos \theta) - 0) + (0 - \frac{1}{2} I \omega^{2}) = 0 \nonumber\]

au

\[\frac{1}{2} I \omega^{2} = mg \frac{L}{2} (1 - \cos \theta) \ldotp \nonumber\]

Kutatua kwa\(\omega\), tuna

\[\omega = \sqrt{mg \frac{L}{I} (1 - \cos \theta)} = \sqrt{mg \frac{L}{\frac{1}{3} mL^{2}} (1 - \cos \theta)} = \sqrt{g \frac{3}{L} (1 - \cos \theta)} \ldotp \nonumber\]

Kuingiza maadili ya namba, tuna

\[\omega = \sqrt{(9.8\; m/s^{2}) \left(\dfrac{3}{0.3\; m}\right) (1 - \cos 30)} = 3.6\; rad/s \ldotp \nonumber\]

Umuhimu

Kumbuka kwamba kasi ya angular ya pendulum haitegemei wingi wake.