10.5: Muda wa Inertia na Nishati ya Kinetic ya mzunguko
- Page ID
- 176914
- Eleza tofauti kati ya nishati ya kinetic ya mzunguko na ya kutafsiri
- Eleza dhana ya kimwili ya wakati wa inertia kwa suala la usambazaji wa wingi kutoka kwa mhimili wa mzunguko
- Eleza jinsi wakati wa inertia ya miili imara huathiri nishati yao ya kinetic ya mzunguko.
- Tumia uhifadhi wa nishati ya mitambo kuchambua mifumo inayofanyika mzunguko na tafsiri.
- Tumia kasi ya angular ya mfumo unaozunguka wakati kuna hasara za nishati kutokana na nguvu zisizo za kihafidhina.
Hadi sasa katika sura hii, tumekuwa tukifanya kazi na kinematics ya mzunguko: maelezo ya mwendo kwa mwili unaozunguka unaozunguka na mzunguko uliowekwa wa mzunguko. Katika sehemu hii, tunafafanua kiasi mbili mpya ambazo zinasaidia kwa kuchambua mali ya vitu vinavyozunguka: wakati wa inertia na nishati ya mzunguko wa kinetic. Kwa mali hizi zinafafanuliwa, tutakuwa na zana mbili muhimu tunayohitaji kwa kuchambua mienendo ya mzunguko.
Rotational Kinetic Nishati
Kitu chochote cha kusonga kina nishati ya kinetic. Tunajua jinsi ya kuhesabu hii kwa mwili unaoendelea na mwendo wa kutafsiri, lakini vipi kuhusu mwili mgumu unaozunguka? Hii inaweza kuonekana ngumu kwa sababu kila hatua kwenye mwili mgumu ina kasi tofauti. Hata hivyo, tunaweza kutumia kasi ya angular ambayo ni sawa kwa mwili mzima rigid- kueleza nishati kinetic kwa kitu kupokezana. Kielelezo\(\PageIndex{1}\) kinaonyesha mfano wa mwili unaozunguka sana: jiwe la umeme linaloendeshwa na magari. Sparks ni kuruka, na kelele na vibration huzalishwa kama grindstone inafanya kazi yake. Mfumo huu una nishati kubwa, baadhi yake kwa namna ya joto, mwanga, sauti, na vibration. Hata hivyo, wengi wa nishati hii ni katika mfumo wa nishati ya kinetic ya mzunguko.
Nishati katika mwendo wa mzunguko sio aina mpya ya nishati; badala yake, ni nishati inayohusishwa na mwendo wa mzunguko, sawa na nishati ya kinetic katika mwendo wa kutafsiri. Hata hivyo, kwa sababu nishati ya kinetic hutolewa na\(K=\frac{1}{2}mv^2\), na kasi ni kiasi ambacho ni tofauti kwa kila hatua kwenye mwili unaozunguka kuhusu mhimili, ni busara kutafuta njia ya kuandika nishati ya kinetic kwa suala la kutofautiana\(\omega\), ambayo ni sawa kwa pointi zote kwenye mwili unaozunguka rigid. Kwa chembe moja inayozunguka karibu na mhimili uliowekwa, hii ni moja kwa moja kuhesabu. Tunaweza kuhusisha kasi ya angular kwa ukubwa wa kasi ya kutafsiri kwa kutumia uhusiano\(v_t=\omega r\), wapi\(r\) umbali wa chembe kutoka kwa mhimili wa mzunguko na\(v_t\) ni kasi yake ya tangential. Kubadilisha katika equation kwa nishati kinetic, tunaona
\[ K=\frac{1}{2} m v_{t}^{2}=\frac{1}{2} m(\omega r)^{2}=\frac{1}{2}\left(m r^{2}\right) \omega^{2}. \nonumber \]
Katika kesi ya mwili unaozunguka rigid, tunaweza kugawanya mwili wowote katika idadi kubwa ya raia ndogo, kila mmoja akiwa\(m_j\) na wingi na umbali wa mzunguko wa mzunguko\(r_j\), kama kwamba molekuli jumla ya mwili ni sawa na jumla ya raia wa mtu binafsi:\(M=\sum_{j} m_{j}\). Kila molekuli ndogo ina kasi ya tangential\(v_j\), ambapo tumeacha usajili\(t\) kwa muda. Nishati ya jumla ya kinetic ya mwili unaozunguka rigid ni
\[ K=\sum_{j} \frac{1}{2} m_{j} v_{j}^{2}=\sum_{j} \frac{1}{2} m_{j}\left(r_{j} \omega_{j}\right)^{2} \nonumber \]
na tangu\(\omega_j = \omega\) kwa watu wote,
\[ K=\frac{1}{2}\left(\sum_{j} m_{j} r_{j}^{2}\right) \omega^{2} . \label{10.16} \]
Vitengo vya Equation\ ref {10.16} ni joules (J). Equation katika fomu hii ni kamili, lakini Awkward; tunahitaji kutafuta njia ya kuzalisha.
Muda wa Inertia
Kama sisi kulinganisha Equation\ ref {10.16} kwa njia sisi aliandika nishati kinetic katika Kazi na Kinetic Nishati, (\(\frac{1}{2}mv^2\)), hii inaonyesha tuna mpya rotational variable kuongeza orodha yetu ya mahusiano yetu kati ya rotational na translational vigezo. Kiasi\(\sum_{j} m_{j} r_{j}^{2}\) ni mwenzake kwa wingi katika equation kwa nishati ya kinetic ya mzunguko. Hii ni neno jipya muhimu kwa mwendo wa mzunguko. Kiasi hiki kinaitwa wakati wa inertia\(I\), na vitengo vya kg·m 2:
\[ I=\sum_{j} m_{j} r_{j}^{2} . \label{10.17} \]
Kwa sasa, tunaacha maneno kwa fomu ya muhtasari, inayowakilisha wakati wa inertia ya mfumo wa chembe za uhakika zinazozunguka kuhusu mhimili uliowekwa. Tunaona kwamba wakati wa inertia ya chembe moja ya uhakika kuhusu mhimili uliowekwa ni tu\(mr^2\), na\(r\) kuwa umbali kutoka kwa chembe ya uhakika hadi mhimili wa mzunguko. Katika sehemu inayofuata, tunachunguza fomu muhimu ya equation hii, ambayo inaweza kutumika kuhesabu wakati wa hali ya miili ya kawaida ya kawaida.
Wakati wa inertia ni kipimo cha upimaji wa inertia ya mzunguko, kama vile katika mwendo wa kutafsiri, na wingi ni kipimo cha upimaji wa inertia-yaani, kitu kikubwa zaidi ni, inertia zaidi ina, na zaidi ni upinzani wake wa mabadiliko katika kasi ya mstari. Vile vile, wakati mkubwa wa hali ya mwili mgumu au mfumo wa chembe, zaidi ni upinzani wake wa mabadiliko katika kasi ya angular kuhusu mhimili uliowekwa wa mzunguko. Inashangaza kuona jinsi wakati wa inertia unatofautiana na r, umbali wa mhimili wa mzunguko wa chembe za wingi katika Equation\ ref {10.17}. Rigid miili na mifumo ya chembe na molekuli zaidi kujilimbikizia katika umbali mkubwa kutoka mhimili wa mzunguko na wakati kubwa ya hali ya miili na mifumo ya wingi huo, lakini kujilimbikizia karibu mhimili wa mzunguko. Kwa njia hii, tunaweza kuona kwamba silinda ya mashimo ina inertia zaidi ya mzunguko kuliko silinda imara ya molekuli sawa wakati unapozunguka kuhusu mhimili kupitia katikati. Kubadilisha Equation\ ref {10.17} katika Equation\ ref {10.16}, kujieleza kwa nishati ya kinetic ya mwili unaozunguka unakuwa
\[ K=\frac{1}{2} I \omega^{2} . \label{10.18} \]
Tunaona kutoka kwa usawa huu kwamba nishati ya kinetic ya mwili unaozunguka imara ni sawa sawa na wakati wa inertia na mraba wa kasi ya angular. Hii hutumiwa katika vifaa vya kuhifadhi nishati ya flywheel, ambavyo vimeundwa kuhifadhi kiasi kikubwa cha nishati ya kinetic inayozunguka. Carmakers wengi sasa kupima flywheel nishati ya kuhifadhi vifaa katika magari yao, kama vile flywheel, au kinetic mfumo wa nishati ahueni, inavyoonekana katika Kielelezo\(\PageIndex{2}\).

Kiasi cha mzunguko na tafsiri kwa nishati ya kinetic na inertia ni muhtasari katika Jedwali 10.4. Safu ya uhusiano haijaingizwa kwa sababu ya mara kwa mara haipo ambayo tunaweza kuzidisha wingi wa mzunguko ili kupata kiasi cha kutafsiri, kama inaweza kufanyika kwa vigezo katika Jedwali 10.3.
| Mzunguko | Tafsiri |
|---|---|
| \(I=\sum_{j} m_{j} r_{j}^{2}\) | \(m\) |
| \(K = \frac{1}{2}I \omega^2\) | \(K = \frac{1}{2} m v^2 \) |
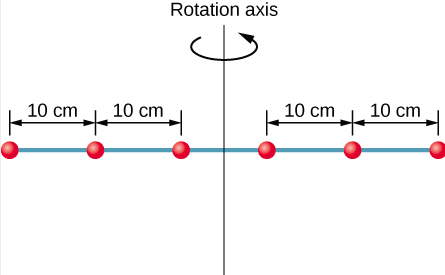
Washers sita wadogo ni spaced 10 cm mbali juu ya fimbo ya molekuli kidogo na 0.5 m urefu. Masi ya kila washer ni 20 g. fimbo huzunguka kuhusu mhimili iko katika cm 25, kama inavyoonekana katika Kielelezo\(\PageIndex{3}\). (a) Ni wakati gani wa hali ya mfumo? (b) Ikiwa washers wawili walio karibu na mhimili huondolewa, ni wakati gani wa inertia ya washers nne zilizobaki? (c) Ikiwa mfumo unao na washers sita huzunguka saa 5 rev/s, ni nishati gani ya mzunguko wa kinetic?
Mkakati
- Tunatumia ufafanuzi kwa muda wa inertia kwa mfumo wa chembe na kufanya muhtasari ili kutathmini kiasi hiki. Raia wote ni sawa ili tuweze kuvuta kiasi hicho mbele ya ishara ya muhtasari.
- Tunafanya hesabu sawa.
- Sisi kuingiza matokeo kutoka (a) katika kujieleza kwa nishati ya kinetic ya mzunguko.
Suluhisho
- \(I=\sum m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}+2 \times(0.05 \: \mathrm{m})^{2}\right)=0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(I=\sum_{j} m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}\right)=0.0034 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(K=\frac{1}{2} I \omega^{2}=\frac{1}{2}\left(0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(5.0 \times 2 \pi \: \mathrm{rad} / \mathrm{s})^{2}=1.73 \: \mathrm{J}\)
Umuhimu
Tunaweza kuona michango ya mtu binafsi kwa wakati wa hali. Misa karibu na mhimili wa mzunguko wana mchango mdogo sana. Tulipowaondoa, ilikuwa na athari ndogo sana wakati wa inertia.
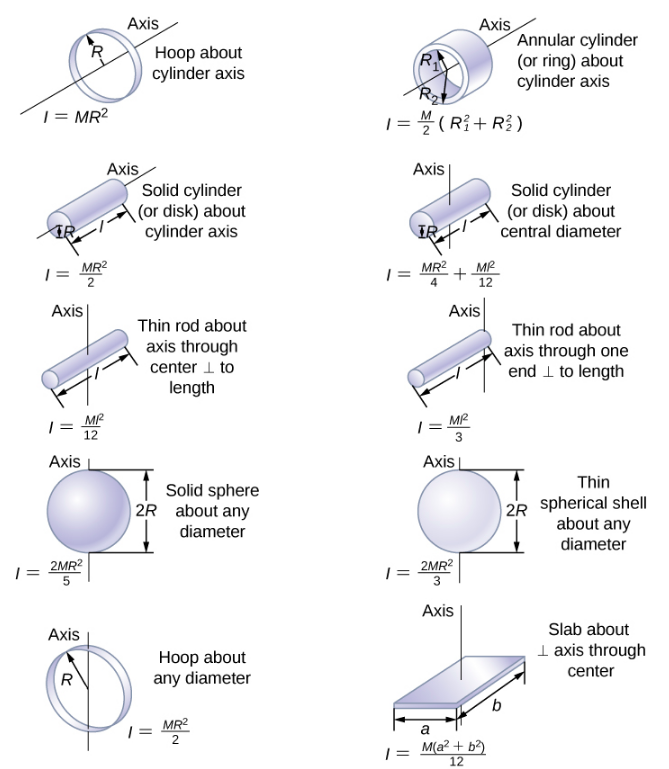
Katika sehemu inayofuata, tunazalisha equation ya summation kwa chembe za uhakika na kuendeleza njia ya kuhesabu wakati wa inertia kwa miili imara. Kwa sasa, ingawa, Kielelezo\(\PageIndex{4}\) inatoa maadili ya inertia rotational kwa maumbo ya kawaida kitu karibu shoka maalum.
Kutumia Nishati ya Kinetic ya mzunguko
Sasa hebu tufanye mawazo ya nishati ya kinetic ya mzunguko na wakati wa meza ya inertia ili kupata hisia kwa nishati inayohusishwa na vitu vichache vinavyozunguka. Mifano zifuatazo pia zitasaidia kukupata vizuri kutumia equations hizi. Kwanza, hebu tuangalie mkakati wa kutatua matatizo kwa nishati ya mzunguko.
- Kuamua kwamba nishati au kazi inahusika katika mzunguko.
- Kuamua mfumo wa maslahi. Mchoro kawaida husaidia.
- Kuchambua hali ili kuamua aina za kazi na nishati zinazohusika.
- Ikiwa hakuna hasara za nishati kutokana na msuguano na majeshi mengine yasiyo ya kihafidhina, nishati ya mitambo imehifadhiwa, yaani,\(K_i + U_i = K_f + U_f\).
- Ikiwa majeshi yasiyo ya kihafidhina yanapo, nishati ya mitambo haihifadhiwa, na aina nyingine za nishati, kama joto na mwanga, zinaweza kuingia au kuacha mfumo. Kuamua ni nini na uhesabu kama inavyohitajika.
- Ondoa maneno popote iwezekanavyo ili kurahisisha algebra.
- Tathmini ufumbuzi wa namba ili uone ikiwa ni busara katika hali ya kimwili iliyotolewa katika maneno ya tatizo.
Helikopta ndogo ya uokoaji ina vile vinne: Kila ni urefu wa 4.00 m na ina uzito wa kilo 50.0 (Kielelezo\(\PageIndex{5}\)). Vipande vinaweza kulinganishwa kama fimbo nyembamba zinazozunguka juu ya mwisho mmoja wa mhimili perpendicular kwa urefu wao. Helikopta ina jumla ya kubeba uzito wa kilo 1000. (a) Tumia nishati ya kinetic ya mzunguko katika vile wakati wanapozunguka saa 300 rpm. (b) Tumia nishati ya kutafsiri kinetic ya helikopta wakati inapita saa 20.0 m/s, na ulinganishe na nishati ya mzunguko katika vile.

Mkakati
Nguvu za kinetic za mzunguko na za kutafsiri zinaweza kuhesabiwa kutoka kwa ufafanuzi wao. Maneno ya tatizo hutoa vipindi vyote muhimu ili kutathmini maneno ya nguvu za mzunguko na za kutafsiri za kinetic.
Suluhisho
a. rotational kinetic nishati ni
\[ K = \frac{1}{2} I \omega^2 \nonumber \]
Lazima tubadilishe kasi ya angular kwa radians kwa pili na kuhesabu wakati wa inertia kabla ya kupata\(K\). Kasi ya angular\(\omega\) ni
\[ \omega=\frac{300 \text { rev }}{1.00 \min } \frac{2 \pi \text { rad }}{1 \text { rev }} \frac{1.00 \: \min }{60.0 \: \mathrm{s}}=31.4 \: \frac{\mathrm{rad}}{\mathrm{s}}. \nonumber \]
Wakati wa inertia ya blade moja ni ile ya fimbo nyembamba iliyozungushwa juu ya mwisho wake, iliyoorodheshwa kwenye Mchoro\(\PageIndex{4}\). Jumla\(I\) ni mara nne wakati huu wa inertia kwa sababu kuna vile vinne. Hivyo,
\[ I=4 \frac{M l^{2}}{3}=4 \times \frac{(50.0 \: \mathrm{kg})(4.00 \: \mathrm{m})^{2}}{3}=1067.0 \: \mathrm{kg} \cdot \mathrm{m}^{2} \nonumber .\]
\(I\)Kuingia\(\omega\) na katika kujieleza kwa nishati ya mzunguko kinetic inatoa
\[ K=0.5\left(1067 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(31.4 \: \mathrm{rad} / \mathrm{s})^{2}=5.26 \times 10^{5} \: \mathrm{J}. \nonumber \]
b Kuingia maadili yaliyotolewa katika equation kwa nishati ya kutafsiri kinetic, tunapata
\[ K=\frac{1}{2} m v^{2}=(0.5)(1000.0 \: \mathrm{kg})(20.0 \: \mathrm{m} / \mathrm{s})^{2}=2.00 \times 10^{5} \: \mathrm{J} . \nonumber \]
Ili kulinganisha nguvu za kinetic, tunachukua uwiano wa nishati ya kutafsiri kinetic kwa nishati ya kinetic inayozunguka. Uwiano huu ni
\[ \frac{2.00 \times 10^{5} \: \mathrm{J}}{5.26 \times 10^{5} \: \mathrm{J}}=0.380 . \nonumber \]
Umuhimu
Uwiano wa nishati ya kutafsiri kwa nishati ya kinetic ya mzunguko ni 0.380 tu. Uwiano huu unatuambia kwamba wengi wa nishati ya kinetic ya helikopta iko katika vile vinavyozunguka.
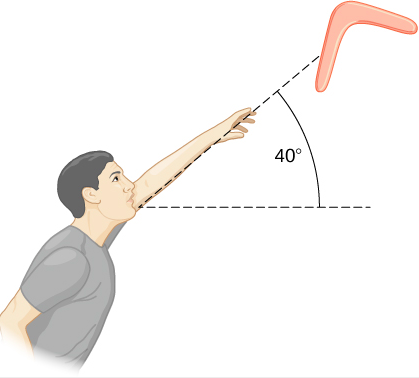
Mtu hupiga boomerang ndani ya hewa kwa kasi ya 30.0 m/s kwa pembe ya 40.0° kwa kuzingatia usawa (Kielelezo\(\PageIndex{6}\)). Ina uzito wa kilo 1.0 na inazunguka saa 10.0 rev/s. wakati wa hali ya boomerang inapewa kama\(I=\frac{1}{12} m L^{2} \) wapi\(L\) = 0.7 m. (a) Nishati ya jumla ya boomerang inapoacha mkono? (b) Boomerang huenda juu gani kutoka kwenye mwinuko wa mkono, kukataa upinzani wa hewa?
Mkakati
Tunatumia ufafanuzi wa nishati ya mzunguko na ya mstari wa kinetic ili kupata nishati ya jumla ya mfumo. Tatizo linasema kupuuza upinzani wa hewa, kwa hivyo hatuna haja ya kuwa na wasiwasi kuhusu kupoteza nishati. Katika sehemu (b), tunatumia uhifadhi wa nishati ya mitambo ili kupata urefu wa juu wa boomerang.
Suluhisho
a Wakati wa inertia:\( I=\frac{1}{12} m L^{2}=\frac{1}{12}(1.0 \: \mathrm{kg})(0.7 \: \mathrm{m})^{2}=0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}. \)
Upeo wa angular:\( \omega=(10.0 \: \mathrm{rev} / \mathrm{s})(2 \pi)=62.83 \: \mathrm{rad} / \mathrm{s} \)
Nishati ya kinetic ya mzunguko ni kwa hiyo
\[ K_{R}=\frac{1}{2}\left(0.041 \: \mathrm{kg} \cdot \mathrm{m}^{2}\right)(62.83 \: \mathrm{rad} / \mathrm{s})^{2}=80.93 \: \mathrm{J} \nonumber \]
Nishati ya kutafsiri kinetic ni
\[ K_{\mathrm{T}}=\frac{1}{2} m v^{2}=\frac{1}{2}(1.0 \: \mathrm{kg})(30.0 \: \mathrm{m} / \mathrm{s})^{2}=450.0 \: \mathrm{J} \nonumber \]
Hivyo, nishati ya jumla katika boomerang ni
\[ K_{\text {Total }}=K_{R}+K_{T}=80.93+450.0=530.93 \: \mathrm{J}. \nonumber \]
b Tunatumia uhifadhi wa nishati ya mitambo. Kwa kuwa boomerang imezinduliwa kwa pembe, tunahitaji kuandika nguvu za jumla za mfumo kwa mujibu wa nguvu zake za kinetic za mstari kwa kutumia kasi katika maelekezo ya x - na y. Nishati ya jumla wakati boomerang inacha mkono ni
\[ E_{\text {Before }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} m v_{y}^{2}+\frac{1}{2} I \omega^{2} \nonumber \]
Nishati ya jumla kwa urefu wa juu ni
\[ E_{\text {Final }}=\frac{1}{2} m v_{x}^{2}+\frac{1}{2} I \omega^{2}+m g h \nonumber \]
Kwa uhifadhi wa nishati ya mitambo,\(E_{Before} = E_{Final}\) hivyo tuna, baada ya kufuta kama maneno,
\[ \frac{1}{2} m v_{y}^{2}=m g h \nonumber .\]
Tangu\(v_y\) = 30.0 m/s (\(\sin 40^{\circ}\)) = 19.28 m/s, tunapata
\[ h=\frac{(19.28 \: \mathrm{m} / \mathrm{s})^{2}}{2\left(9.8 \: \mathrm{m} / \mathrm{s}^{2}\right)}=18.97 \: \mathrm{m} \nonumber \]
Umuhimu
Katika sehemu (b), suluhisho linaonyesha jinsi uhifadhi wa nishati ni njia mbadala ya kutatua tatizo ambalo kwa kawaida litatatuliwa kwa kutumia kinematiki. Kutokuwepo kwa upinzani wa hewa, nishati ya kinetic ya mzunguko haikuwa sababu katika suluhisho kwa urefu wa juu.
Propeller ya nyuklia ya nyuklia ina muda wa inertia ya kilo 800.0 • m 2. Ikiwa propeller iliyojaa ina kiwango cha mzunguko wa 4.0 rev/s wakati inji inapokatwa, ni kiwango gani cha mzunguko wa propeller baada ya 5.0 s wakati upinzani wa maji umechukua 50,000 J nje ya mfumo?


