4.4: Mwendo wa Projectile

Last updated
Save as PDF

Page ID: 176982

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tumia mwendo mmoja wa mwelekeo katika maelekezo ya perpendicular kuchambua mwendo wa projectile.
Tumia upeo, wakati wa kukimbia, na urefu wa juu wa projectile inayozinduliwa na huathiri uso wa gorofa, usio na usawa.
Kupata muda wa kukimbia na athari kasi ya projectile kwamba ardhi katika urefu tofauti na ile ya uzinduzi.
Tumia trajectory ya projectile.

Mwendo wa projectile ni mwendo wa kitu kilichoponywa au kilichopangwa ndani ya hewa, chini ya kuongeza kasi tu kutokana na mvuto. Matumizi ya mwendo wa projectile katika fizikia na uhandisi ni nyingi. Baadhi ya mifano ni pamoja na vimondo wanapoingia katika anga ya Dunia, fireworks, na mwendo wa mpira wowote katika michezo. Vitu vile huitwa projectiles na njia yao inaitwa trajectory. Mwendo wa vitu vya kuanguka kama ilivyojadiliwa katika Motion Along a Straight Line ni rahisi moja-dimensional aina ya mwendo projectile ambayo hakuna harakati usawa. Katika sehemu hii, tunazingatia mwendo wa projectile mbili-dimensional, na matibabu yetu hupuuza madhara ya upinzani wa hewa.

Ukweli muhimu zaidi kukumbuka hapa ni kwamba mwendo pamoja na axes perpendicular ni huru na hivyo inaweza kuchambuliwa tofauti. Tulijadili ukweli huu katika Vectors ya Uhamisho na Velocity, ambapo tuliona kwamba mwendo wa wima na usawa ni huru. Funguo la kuchunguza mwendo wa projectile mbili-dimensional ni kuivunja katika mwendo mbili: moja pamoja na mhimili usawa na nyingine pamoja na wima. (Uchaguzi huu wa axes ni busara zaidi kwa sababu kuongeza kasi kutokana na mvuto ni wima; hivyo, hakuna kasi kwenye mhimili usawa wakati upinzani wa hewa ni duni.) Kama ilivyo desturi, tunaita mhimili usio na usawa wa x-axis na mhimili wima wa y-axis. Haihitajiki kwamba tunatumia uchaguzi huu wa axes; ni rahisi tu katika kesi ya kuongeza kasi ya mvuto. Katika hali nyingine tunaweza kuchagua seti tofauti ya axes. Kielelezo$\PageIndex{1}$ unaeleza nukuu kwa ajili ya makazi yao, ambapo sisi$\vec{s}$ kufafanua kuwa makazi ya jumla,$\vec{x}$ na$\vec{y}$ ni vectors sehemu yake pamoja shoka usawa na wima, kwa mtiririko huo. Ukubwa wa wadudu hawa ni s, x, na y.

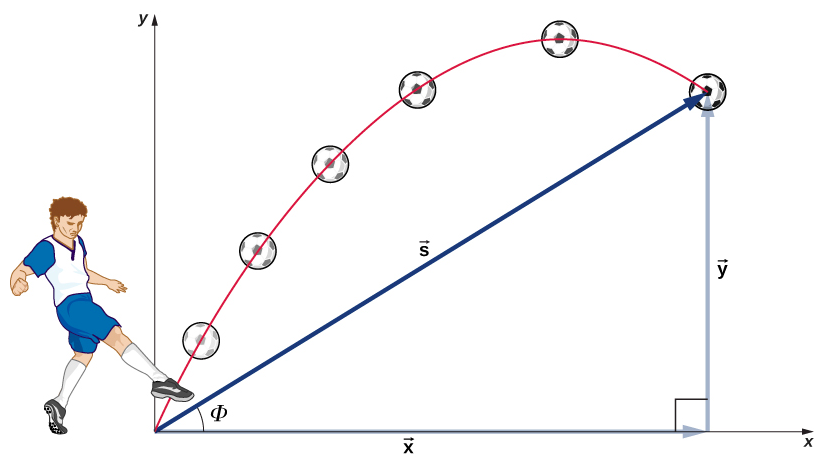
Mfano wa mchezaji wa soka akipiga mpira. Mguu wa mchezaji wa soka ni asili ya mfumo wa kuratibu x y. Trajectory ya mpira wa soka na eneo lake kwa muda wa 6 kwa wakati huonyeshwa. Trajectory ni parabola. Vector s ni makazi yao kutoka asili kwa nafasi ya mwisho ya mpira wa soka. Vector s na vipengele vyake vya x na y huunda pembetatu sahihi, na s kama hypotenuse na pembe phi kati ya mhimili x na s. — Kielelezo$\PageIndex{1}$: jumla ya makazi yao s ya mpira wa soka katika hatua kando ya njia yake. Vector$\vec{s}$ ina vipengele$\vec{x}$ na$\vec{y}$ pamoja na axes usawa na wima. Ukubwa wake ni s na hufanya angle$\phi$ na usawa.

Ili kuelezea mwendo wa projectile kabisa, lazima tujumuishe kasi na kuongeza kasi, pamoja na uhamisho. Lazima tupate vipengele vyao pamoja na x- na y-axes. Hebu tuchukue nguvu zote isipokuwa mvuto (kama vile upinzani wa hewa na msuguano, kwa mfano) ni duni. Kufafanua mwelekeo mzuri kuwa juu, vipengele vya kuongeza kasi ni rahisi sana:

\[a_{y} = −g = −9.8\; m/s^{2} (− 32\; ft/s^{2}) \ldotp\]

Kwa sababu mvuto ni wima, _x = 0. Kama _x = 0, hii ina maana kasi ya awali katika mwelekeo x ni sawa na kasi ya mwisho katika mwelekeo x, au v _x = v _0x. Kwa hali hizi juu ya kuongeza kasi na kasi, tunaweza kuandika equation kinematic 4.11 kupitia Equation 4.18 kwa mwendo katika uwanja sare mvuto, ikiwa ni pamoja na wengine wa milinganyo kinematic kwa kuongeza kasi ya mara kwa mara kutoka Motion na Kuongeza kasi ya mara kwa mara. Ulinganisho wa kinematic kwa mwendo katika uwanja wa mvuto sare huwa milinganyo ya kinematic na _y = -g, _x = 0:

Mzunguko wa usawa

\[v_{0x} = v_{x}, \quad x = x_{0} + v_{x} t \label{4.19}\]

Mwendo wa wima

\[y = y_{0} + \frac{1}{2} (v_{0y} + v_{y})t \label{4.20}\]

\[v_{y} = v_{0y} - gt \label{4.21}\]

\[y = y_{0} + v_{0y} t - \frac{1}{2} g t^{2} \label{4.22}\]

\[v_{y}^{2}= v_{0y}^{2} + 2g(y − y_{0}) \label{4.23}\]

Kutumia seti hii ya equations, tunaweza kuchambua mwendo wa projectile, kukumbuka baadhi ya pointi muhimu.

Mkakati wa Kutatua matatizo: Mwendo wa Projectile

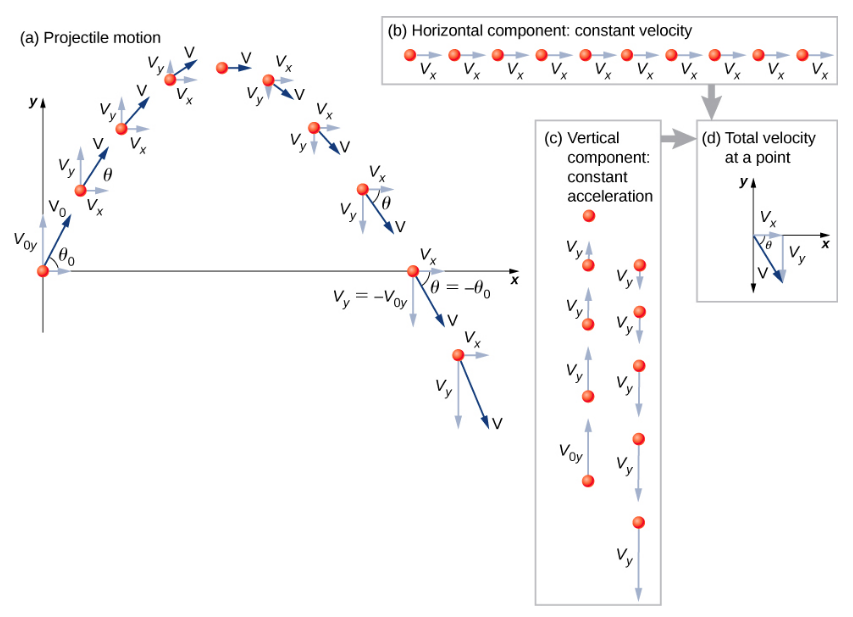
Tatua mwendo katika vipengele vya usawa na wima pamoja na x- na y-axes. Ukubwa wa vipengele vya uhamisho$\vec{s}$ pamoja na shoka hizi ni x na y. ukubwa wa vipengele vya kasi$\vec{v}$ ni v _x = vcos$\theta$ na v _y = vsin$\theta$, ambapo v ni ukubwa wa kasi na$\theta$ ni mwelekeo wake kuhusiana na usawa, kama inavyoonekana katika Kielelezo$\PageIndex{2}$.
Tumia mwendo kama mwendo wa kujitegemea wa mwelekeo mmoja: moja ya usawa na wima nyingine. Tumia usawa wa kinematic kwa mwendo usio na usawa na wima uliowasilishwa mapema.
Tatua kwa haijulikani katika mwendo mawili tofauti: moja ya usawa na moja ya wima. Kumbuka kuwa tu ya kawaida kutofautiana kati ya mwendo ni wakati t. taratibu za kutatua matatizo hapa ni sawa na zile za kinematics moja-dimensional na ni mfano katika mifano zifuatazo kutatuliwa.
Rejesha kiasi katika maelekezo ya usawa na wima ili kupata uhamisho wa jumla$\vec{s}$ na kasi$\vec{v}$. Kutatua kwa ukubwa na mwelekeo wa makazi yao na kasi kwa kutumia $$s =\ sqrt {x^ {2} + y ^ {2}}\ ldotp\ quad\ phi =\ tan^ {-1}\ kushoto (\ dfrac {y} {x}\ haki),\ quad v =\ sqrt {v_ {x} ^ {2} + v_ {y} ^ {2}} ldotp $$wapi$\phi$ mwelekeo wa makazi yao$\vec{s}$.

Kielelezo a inaonyesha maeneo na kasi ya projectile kwenye mfumo x y kuratibu katika 10 instants kwa wakati. Wakati projectile ni katika asili, ina kasi v ndogo 0 y ambayo inafanya angle theta ndogo 0 na usawa. Kasi inaonyeshwa kama mshale wa buluu giza, na sehemu zake x na y zinaonyeshwa kama mshale mwembamba wa buluu. msimamo projectile ifuatavyo chini-ufunguzi parabola, kusonga hadi urefu upeo, kisha nyuma y = 0, na kuendelea chini x mhimili kasi, V, katika kila wakati hufanya theta angle ambayo mabadiliko katika muda, na ina x sehemu V ndogo x na y sehemu v ndogo y. x sehemu ya kasi V ndogo x x ni sawa wakati wote. Sehemu y v ndogo y inaonyesha juu lakini inakuwa ndogo, mpaka projectile kufikia urefu wa juu, ambapo kasi ni ya usawa na haina sehemu y. Baada ya urefu upeo, kasi ina y sehemu akizungumzia chini na kukua kubwa. Kama projectile inafikia mwinuko sawa njiani chini kama ilivyokuwa njiani juu, kasi yake iko chini ya mlalo kwa angle sawa theta kama ilivyokuwa juu ya usawa njiani juu. Hasa, linapokuja nyuma y = 0 njiani chini, angle kati ya vector v na usawa ni minus s=theta ndogo zero na y sehemu ya kasi ni bala v ndogo 0 y. nafasi ya mwisho inavyoonekana ni chini x mhimili, na y sehemu ya kasi ni kubwa kuliko ilivyokuwa awali. Grafu inaonyesha wazi kwamba umbali usawa kusafiri katika kila moja ya vipindi wakati ni sawa, wakati umbali wima kupungua juu ya njia ya juu na kuongezeka juu ya njia ya chini. Kielelezo b kinaonyesha sehemu ya usawa, kasi ya mara kwa mara. Nafasi za usawa na vipengele x vya kasi ya projectile zinaonyeshwa kwenye mstari usio na usawa. Nafasi hizo zimewekwa sawasawa, na vipengele vya x vya kasi ni sawa, na vinaelezea haki. Kielelezo c kinaonyesha sehemu ya wima, kasi ya mara kwa mara. Nafasi za wima na y vipengele vya kasi ya projectile vinaonyeshwa kwenye mstari wa wima. Nafasi ni kupata karibu pamoja juu ya njia ya juu, kisha zaidi mbali juu ya njia ya chini. Vipengele y vya kasi vya awali vinaelezea, kupungua kwa ukubwa mpaka hakuna sehemu y kwa kasi kwa urefu wa juu. Baada ya urefu wa juu, vipengele vya y vya kasi vinazidi chini na kuongezeka kwa ukubwa. Kielelezo d inaonyesha kwamba kuweka vipengele usawa na wima ya takwimu b na c pamoja anatoa kasi jumla katika hatua. kasi V ina x sehemu ya V ndogo x, ina y sehemu ya V ndogo y, na hufanya angle ya theta kwa usawa. Katika mfano umeonyeshwa, kasi ina sehemu ya kushuka y. — Kielelezo$\PageIndex{2}$: (a) Sisi kuchambua mbili-dimensional projectile mwendo kwa kuvunja katika mbili kujitegemea moja dimensional mwendo pamoja axes wima na usawa. (b) Mwendo usio na usawa ni rahisi, kwa sababu _x = 0 na v _x ni mara kwa mara. (c) Kasi katika mwelekeo wima huanza kupungua kama kitu kinaongezeka. Katika hatua yake ya juu, kasi ya wima ni sifuri. Kama kitu kinaanguka kuelekea Dunia tena, kasi ya wima inaongezeka tena kwa ukubwa lakini inaashiria katika mwelekeo kinyume na kasi ya awali ya wima. (d) Mabadiliko ya x na y yanarejeshwa ili kutoa kasi ya jumla katika hatua yoyote iliyotolewa kwenye trajectory.

Mfano 4.7: Projectile Fireworks hulipuka juu na mbali

Wakati wa kuonyesha fireworks, shell ni risasi katika hewa na kasi ya awali ya 70.0 m/s kwa angle ya 75.0° juu ya usawa, kama inavyoonekana katika Kielelezo$\PageIndex{3}$. Fyuzi ni wakati muafaka wa kuwaka shell kama inavyofikia kiwango chake cha juu juu juu ya ardhi. (a) Tumia urefu ambao shell hupuka. (b) Ni muda gani unapita kati ya uzinduzi wa shell na mlipuko? (c) Uhamisho wa usawa wa shell unapopuka ni nini? (d) Je, ni makazi ya jumla kutoka hatua ya uzinduzi hadi hatua ya juu?

Trajectory ya shell fireworks kutoka uzinduzi wake hadi hatua yake ya juu inavyoonekana kama nusu ya kushoto ya parabola chini ya ufunguzi katika grafu ya y kama kazi ya x. urefu wa juu ni h = 233 mita na makazi yake x wakati huo ni x = 125 mita. Vector ya awali ya kasi v ndogo 0 ni juu na kulia, tangent kwa Curve trajectory, na hufanya angle ya theta ndogo 0 sawa na digrii 75. — Kielelezo$\PageIndex{3}$: Trajectory ya shell fireworks. Fuse imewekwa kulipuka shell kwenye hatua ya juu katika trajectory yake, ambayo inapatikana kuwa urefu wa 233 m na 125 m mbali kwa usawa.

Mkakati

Mwendo unaweza kuvunjwa katika mwendo usawa na wima ambapo _x = 0 na _y = -g.Tunaweza kisha kufafanua x ₀ na y ₀ kuwa sifuri na kutatua kwa kiasi taka.

Suluhisho

Kwa “urefu” tunamaanisha urefu au nafasi ya wima y juu ya hatua ya mwanzo. Sehemu ya juu katika trajectory yoyote, inayoitwa kilele, inafikiwa wakati v _y = 0. Kwa kuwa tunajua kasi ya awali na ya mwisho, pamoja na nafasi ya awali, tunatumia equation ifuatayo ili kupata y: $$v_ {y} ^ {2} = v_ {0y} ^ {2} - 2g (y - y_ {0})\ ldOTP $$Kwa sababu y ₀ na v _y ni sifuri, equation inafungua kwa $0 = v_ {0y} ^ 2 {} - 2gy\ ldOTP $kutatua kwa y anatoa $y =\ frac {v_ {0y} ^ {2}} {2g}\ lDotP$$Sasa tunapaswa kupata v _0y, sehemu ya kasi ya awali katika mwelekeo y. Inatolewa na v _0y = v ₀ dhambi$\theta_{0}$, ambapo v ₀ ni kasi ya awali ya 70.0 m/s na$\theta_{0}$ = 75° ni angle ya awali. Hivyo $v_ {0y} = v_ {0}\ dhambi\ theta = (70.0\; m/s)\ dhambi 75^ {o} = 67.6\; m/s $$ na y ni $y =\ frac {(67.6\; m/s) ^ {2}} {2 (9.80\; m/s ^ {2})}\ LDOTP $Hivyo, tuna $$y = 233\; m\ ldOTP $$Kumbuka kuwa kwa sababu ya juu ni chanya, kasi ya awali ya wima ni chanya, kama urefu wa juu, lakini kuongeza kasi kusababisha kutoka mvuto ni hasi. Kumbuka pia kwamba urefu wa juu unategemea tu sehemu ya wima ya kasi ya awali, ili projectile yoyote yenye sehemu ya wima ya awali ya 67.6-m/s kufikia urefu wa juu wa 233 m (kupuuza upinzani wa hewa). Nambari katika mfano huu ni busara kwa maonyesho makubwa ya moto, maganda ambayo yanafikia urefu huo kabla ya kulipuka. Katika mazoezi, upinzani wa hewa sio duni kabisa, hivyo kasi ya awali ingekuwa kubwa zaidi kuliko ile iliyotolewa kufikia urefu sawa.
Kama ilivyo katika matatizo mengi ya fizikia, kuna njia zaidi ya moja ya kutatua kwa wakati projectile inafikia hatua yake ya juu. Katika kesi hii, njia rahisi ni kutumia v _y = v _0y - gt. Kwa sababu v _y = 0 kwenye kilele, equation hii inapunguza $0 = v_ {0y} - gt $$au $$t =\ frac {v_ {0y}} {g} =\ frac {67.6\; m/s} {9.80\; m/s^ {2}} = 6.90\; s\ lDOTP $Wakati huu pia ni busara kwa fireworks kubwa. Ikiwa una uwezo wa kuona uzinduzi wa fireworks, angalia kwamba sekunde kadhaa hupita kabla ya shell kulipuka. Njia nyingine ya kutafuta muda ni kwa kutumia y = y ₀ +$\frac{1}{2}$ (v _0y + v _y) t Hii imesalia kwako kama zoezi la kukamilisha.
Kwa sababu upinzani wa hewa ni mdogo, _x = 0 na kasi ya usawa ni mara kwa mara, kama ilivyojadiliwa mapema. Uhamisho wa usawa ni kasi ya usawa inayoongezeka kwa wakati kama iliyotolewa na x = x ₀ + v _x t, ambapo x ₀ ni sawa na sifuri. Hivyo, $$x = v_ {x} t, $$ ambapo v _x ni x-sehemu ya kasi, ambayo hutolewa na $$ v_ {x} = v_ {0}\ cos\ theta = (70.0\; m/s)\ cos 75^ {o} = 18.1\; m/s\ LDOTP $$ wakati t kwa ajili ya mwendo wote ni sawa, hivyo x ni $$x = (18.1 .1\; m/s) (6.90\; s) = 125\; m\ LDOTP$mwendo wa usawa ni kasi ya mara kwa mara katika kutokuwepo kwa upinzani wa hewa. Uhamisho usio na usawa unaopatikana hapa unaweza kuwa na manufaa katika kuweka vipande vya fireworks kutoka kuanguka kwa watazamaji. Wakati shell hupuka, upinzani wa hewa una athari kubwa, na vipande vingi vinatembea moja kwa moja chini.
Vipengele vya usawa na wima vya uhamisho vilihesabiwa tu, hivyo kila kitu kinachohitajika hapa ni kupata ukubwa na mwelekeo wa makazi yao kwa kiwango cha juu: $$\ vec {s} = 125\ kofia {i} + 233\ kofia {j} $$$|\ vec {s} | =\ sqrt {125^ {2} + 233^ {2}} = 264\; m $$$$\ theta =\ tan^ {-1}\ kushoto (\ dfrac { 233} {125}\ haki) = 61.8^ {o}\ lDOTP $$Kumbuka kuwa angle ya vector ya uhamisho ni chini ya angle ya awali ya uzinduzi. Ili kuona kwa nini hii ni, tathmini Kielelezo$\PageIndex{1}$, ambayo inaonyesha curvature ya trajectory kuelekea ngazi ya chini. Wakati wa kutatua Mfano 4.7 (a), maneno tuliyopata kwa y halali kwa mwendo wowote wa projectile wakati upinzani wa hewa hauna maana. Piga urefu wa juu y = h Kisha, $$h =\ frac {v_ {0y} ^ {2}} {2g}\ lDotP$$Ulinganyo huu unafafanua urefu wa juu wa projectile juu ya nafasi yake ya uzinduzi na inategemea tu sehemu ya wima ya kasi ya awali.

Zoezi 4.3

Mwamba unatupwa kwa usawa mbali na mwamba 100.0 m juu na kasi ya 15.0 m/s. (a) Eleza asili ya mfumo wa kuratibu. (b) Ni equation gani inaelezea mwendo usawa? (c) Ambayo equations kuelezea mwendo wima? (d) Kasi ya mwamba ni nini katika hatua ya athari?

Mfano 4.8: Kuhesabu mwendo wa projectile- Mchezaji wa Tennis

Mchezaji wa tenisi atashinda mechi katika uwanja wa Arthur Ashe na anapiga mpira ndani ya anasimama saa 30 m/s na kwa angle 45° juu ya usawa (Kielelezo$\PageIndex{4}$). Njiani chini, mpira unachukuliwa na mtazamaji 10 m juu ya mahali ambapo mpira ulipigwa. (a) Tumia muda unachukua mpira wa tenisi kufikia mtazamaji. (b) Ni ukubwa na mwelekeo wa kasi ya mpira katika athari gani?

Mfano wa mpira wa tenisi ilizinduliwa kwenye safu. mchezaji ni upande wa kushoto wa anasimama na hits mpira juu na kulia katika pembe ya theta sawa na 45 digrii na kasi ya v ndogo 0 sawa na 30 mita kwa sekunde. Mpira hufikia mtazamaji ambaye ameketi mita 10 juu ya urefu wa awali wa mpira. — Kielelezo$\PageIndex{4}$: Trajectory ya mpira wa tenisi hupiga ndani ya kusimama.

Mkakati

Tena, kutatua mwendo huu mbili-dimensional katika harakati mbili za kujitegemea moja-dimensional inatuwezesha kutatua kwa kiasi kinachohitajika. Wakati projectile iko hewani inasimamiwa na mwendo wake wa wima pekee. Hivyo, sisi kutatua kwa mara ya kwanza. Wakati mpira unapoongezeka na kuanguka kwa wima, mwendo usio na usawa unaendelea kwa kasi ya mara kwa mara. Mfano huu unauliza kasi ya mwisho. Kwa hiyo, tunajumuisha matokeo ya wima na ya usawa ili kupata$\vec{v}$ wakati wa mwisho t, uliowekwa katika sehemu ya kwanza ya mfano.

Suluhisho

Wakati mpira upo hewani, huinuka na kisha huanguka kwenye nafasi ya mwisho 10.0 m juu kuliko urefu wake wa kuanzia. Tunaweza kupata muda wa hii kwa kutumia Equation\ ref {4.22}: $$y = y_ {0} + v_ {0y} t -\ frac {1} {2} gt^ {2}\ ldOTP $Kama sisi kuchukua nafasi ya awali y ₀ kuwa sifuri, basi nafasi ya mwisho ni y = 10 m. {0y} = v_ {0}\ dhambi\ theta_ {0} = (30.0\; m/s)\ dhambi 45^ {o} = 21.2\; m/s\ lDotP$$ Kubadilisha katika Equation\ ref {4.22} kwa y inatupa $10.0\; m = (21.2\; m/s) t - (4.90\; m/s^ {2}) t^ {2}\ LDOTP $$upya masharti hutoa quadrrr equation ya atiki katika t: $$ (4.90\; m/s^ {2}) t^ {2} - (21.2\; m/s) t + 10.0\; m = 0\ lDOTP$Matumizi ya formula ya quadratic mavuno t = 3.79 s na t = 0.54 s Tangu mpira ni katika urefu wa 10 m mara mbili wakati trajectory yake-mara moja juu ya njia ya juu na mara moja juu ya njia chini-sisi kuchukua ufumbuzi tena kwa muda inachukua mpira kufikia mtazamaji: $$t = 3.79\; s\ lDotP $Wakati wa mwendo wa projectile umeamua kabisa na mwendo wima. Kwa hiyo, projectile yoyote ambayo ina kasi ya wima ya awali ya 21.2 m/s na ardhi 10.0 m juu ya urefu wake wa kuanzia hutumia 3.79 s hewa.
Tunaweza kupata mwisho usawa na wima kasi v _x na v _y na matumizi ya matokeo kutoka (a). Kisha, tunaweza kuchanganya ili kupata ukubwa wa vector jumla ya kasi$\vec{v}$ na angle$\theta$ inafanya kwa usawa. Tangu v _x ni mara kwa mara, tunaweza kutatua kwa ajili yake katika eneo lolote usawa. Tunachagua hatua ya kuanzia kwa sababu tunajua kasi ya awali na angle ya awali. Kwa hiyo, $$ v_ {x} = v_ {0}\ cos\ theta_ {0} = (30\; m/s)\ cos 45^ {o} = 21.2\; m/s\ LDOTP $Kasi ya mwisho ya wima imetolewa na Equation\ ref {4.21}: $$v_ {y} = v_ {0y} - gt\ LdOTP $Tangu$v_{0y}$ ilipatikana katika sehemu (a) kuwa 21.2 m/s, tuna $v_ {y} = 21.2\; m/s- (9.8\; m/s^ {2}) (3.79 s) = -15.9\; m/s\ ldotp$$ Ukubwa wa kasi ya mwisho$\vec{v}$ ni $$v =\ sqrt {v_ {x} ^ {2} + v_ {y} ^ {2}} =\ sqrt {(21.2\; m/s) ^ {2} + (-15.9\; m/s) ^ {2}} = 26.5\; m/s\ LDOTP $Mwelekeo$\theta_{v}$ unapatikana kwa kutumia tangent inverse: $$\ theta_ {v} =\ tan^ {-1}\ kushoto (\ dfrac {v_ {y}} {v_ {x}}\ haki) =\ tan^ {-1}\ kushoto (\ dfrac {21.2} {-15.9}\ haki) = -53.1^ {o}\ ldotp $$

Umuhimu

Kama ilivyoelezwa hapo awali, wakati wa mwendo wa projectile umeamua kabisa na mwendo wa wima. Kwa hiyo, projectile yoyote ambayo ina kasi ya wima ya awali ya 21.2 m/s na ardhi 10.0 m juu ya urefu wake wa kuanzia hutumia 3.79 s hewa.
Pembe hasi inamaanisha kasi iko 53.1° chini ya usawa kwenye hatua ya athari. Matokeo haya ni sawa na ukweli kwamba mpira unaathiri kwa hatua upande wa pili wa kilele cha trajectory na kwa hiyo ina hasi y sehemu ya kasi. Ukubwa wa kasi ni chini ya ukubwa wa kasi ya awali tunayotarajia kwani inaathiri 10.0 m juu ya mwinuko wa uzinduzi.

Muda wa kukimbia, trajectory, na Upeo

Ya riba ni wakati wa kukimbia, trajectory, na aina mbalimbali kwa projectile ilizinduliwa juu ya uso gorofa usawa na athari juu ya uso huo. Katika kesi hii, equations ya kinematic hutoa maneno muhimu kwa kiasi hiki, ambacho hutolewa katika sehemu zifuatazo.

Muda wa kukimbia

Tunaweza kutatua wakati wa kukimbia kwa projectile ambayo imezinduliwa na athari juu ya uso gorofa usawa kwa kufanya baadhi ya manipulations ya equations kinematic. Tunaona nafasi na uhamisho katika y lazima iwe sifuri wakati wa uzinduzi na athari kwenye uso hata. Hivyo, sisi kuweka makazi yao katika y sawa na sifuri na kupata

\[y − y_{0} = v_{0y} t − \frac{1}{2} gt^{2} = (v_{0} \sin \theta_{0})t − \frac{1}{2} gt^{2} = 0 \ldotp\]

Factoring, tuna

\[t \left(v_{0} \sin \theta_{0} - \dfrac{gt}{2}\right) = 0 \ldotp\]

Kutatua kwa ajili yake inatupa

\[T_{tof} = \frac{2(v_{0} \sin \theta_{0})}{g} \ldotp \label{4.24}\]

Huu ndio wakati wa kukimbia kwa projectile iliyozinduliwa na kuathiri uso wa gorofa usawa. Equation\ ref {4.24} haina kuomba wakati projectile ardhi katika mwinuko tofauti kuliko ilizinduliwa, kama tulivyoona katika Mfano 4.8 ya mchezaji wa tenisi kupiga mpira ndani ya anasimama. Suluhisho lingine, t = 0, linalingana na wakati wa uzinduzi. Wakati wa kukimbia ni linearly sawia na kasi ya awali katika mwelekeo y na inversely sawia na g Hivyo, juu ya mwezi, ambapo mvuto ni moja ya sita ile ya Dunia, projectile ilizinduliwa kwa kasi sawa na duniani itakuwa dhuru mara sita kwa muda mrefu.

Trajectory

Trajectory ya projectile inaweza kupatikana kwa kuondoa muda wa kutofautiana t kutoka kwa usawa wa kinematic kwa t holela na kutatua kwa y (x). Tunachukua x ₀ = y ₀ = 0 hivyo projectile imezinduliwa kutoka asili. Equation ya kinematic kwa x inatoa

\[x = v_{0x}t \Rightarrow t = \frac{x}{v_{0x}} = \frac{x}{v_{0} \cos \theta_{0}} \ldotp\]

Kubadilisha maneno kwa t katika equation kwa nafasi y = (v ₀ dhambi$\theta_{0}$) t -$\frac{1}{2}$ gt ² inatoa

\[y = (v_{0} \sin \theta_{0}) \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right) - \frac{1}{2} g \left(\dfrac{x}{v_{0} \cos \theta_{0}}\right)^{2} \ldotp\]

Rearranging masharti, tuna

\[y = (\tan \theta_{0})x - \Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big] x^{2} \ldotp \label{4.25}\]

Equation hii ya trajectory ni ya fomu y = ax + bx ², ambayo ni equation ya parabola na coefficients

\[a = \tan \theta_{0}, \quad b = - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \ldotp\]

Range

Kutoka equation trajectory tunaweza pia kupata mbalimbali, au umbali usawa kusafiri na projectile. Factoring Equation\ ref {4.25}, tuna

\[y = x \Big[ \tan \theta_{0} - \frac{g}{2(v_{0} \cos \theta_{0})^{2}} x \Big] \ldotp\]

Msimamo y ni sifuri kwa hatua zote za uzinduzi na hatua ya athari, kwani sisi tena tunazingatia tu uso wa gorofa usawa. Kuweka y = 0 katika equation hii inatoa ufumbuzi x = 0, sambamba na hatua ya uzinduzi, na

\[x = \frac{2 v_{0}^{2} \sin \theta_{0} \cos \theta_{0}}{g} ,\]

sambamba na hatua ya athari. Kutumia utambulisho wa trigonometric 2sin$\theta$ cos$\theta$ = sin2$\theta$ na kuweka x = R kwa upeo, tunapata

\[R = \frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \ldotp \label{4.26}\]

Kumbuka hasa kwamba Equation\ ref {4.26} halali tu kwa uzinduzi na athari juu ya uso usawa. Tunaona mbalimbali ni moja kwa moja sawia na mraba wa kasi ya awali v ₀ na dhambi ²$\theta_{0}$, na ni inversely sawia na kuongeza kasi ya mvuto. Hivyo, juu ya Mwezi, upeo huo utakuwa mara sita zaidi kuliko duniani kwa kasi sawa ya awali. Zaidi ya hayo, tunaona kutokana na sababu dhambi ²$\theta_{0}$ kwamba mbalimbali ni upeo katika 45°. Matokeo haya yanaonyeshwa kwenye Kielelezo$\PageIndex{5}$. Katika (a) tunaona kwamba kasi kubwa ya awali, ni kubwa zaidi. Katika (b), tunaona kwamba upeo ni wa juu katika 45°. Hii ni kweli tu kwa hali ya kupuuza upinzani wa hewa. Ikiwa upinzani wa hewa unazingatiwa, angle ya juu ni ndogo sana. Inashangaza kwamba upeo huo unapatikana kwa pembe mbili za uzinduzi wa awali ambazo zinafikia 90°. Projectile ilizinduliwa kwa angle ndogo ina kilele cha chini kuliko angle ya juu, lakini wote wawili wana aina sawa.

Kielelezo a inaonyesha trajectories ya projectiles ilizindua saa moja ya awali 45 shahada angle juu usawa na tofauti kasi ya awali. Trajectories zinaonyeshwa kutoka uzinduzi hadi kutua nyuma kwenye mwinuko wa awali. Katika machungwa ni trajectory kwa mita 30 kwa pili, kutoa mbalimbali R (umbali kutoka uzinduzi hadi kutua) ya 91.8 m Katika zambarau ni trajectory kwa mita 40 kwa pili, kutoa mbalimbali R ya 163 m Katika bluu ni trajectory kwa mita 50 kwa pili, kutoa mbalimbali R ya 255 m urefu wa juu wa projectile huongezeka kwa kasi ya awali. Kielelezo b kinaonyesha trajectories ya projectiles ilizinduliwa kwa kasi sawa ya awali ya mita 50 kwa pembe ya pili na tofauti ya uzinduzi. Trajectories zinaonyeshwa kutoka uzinduzi hadi kutua nyuma kwenye mwinuko wa awali. Katika machungwa ni trajectory kwa angle ya digrii 15 juu ya usawa, kutoa mbalimbali R ya 128 m Katika zambarau ni trajectory kwa angle ya digrii 45 juu ya usawa, kutoa mbalimbali R ya 255 m Katika bluu ni trajectory kwa angle ya digrii 75 juu ya usawa, kutoa mbalimbali R ya 128 m, sawa na kwa trajectory shahada 15. Urefu wa juu huongezeka kwa angle ya uzinduzi. — Kielelezo$\PageIndex{5}$: Trajectories ya projectiles juu ya ardhi ngazi. (a) zaidi ya awali kasi v ₀, zaidi mbalimbali kwa ajili ya kupewa angle ya awali. (b) Athari ya angle ya awali (\ theta_ {0}\) juu ya kiwango cha projectile na kasi ya awali iliyotolewa. Kumbuka kuwa upeo huo ni sawa kwa pembe za awali za 15° na 75°, ingawa urefu wa juu wa njia hizo ni tofauti.

Mfano 4.9: Kulinganisha shots za golf

Golfer anajikuta katika hali mbili tofauti kwenye mashimo tofauti. Kwenye shimo la pili yeye ni 120 m kutoka kijani na anataka kugonga mpira 90 m na basi ni kukimbia kwenye kijani. Yeye pembe risasi chini ya ardhi katika 30° kwa usawa basi mpira roll baada ya athari. Kwenye shimo la nne yeye ni 90 m kutoka kijani na anataka kuruhusu mpira kuacha kwa kiwango cha chini cha rolling baada ya athari. Hapa, yeye pembe risasi katika 70° kwa usawa ili kupunguza rolling baada ya athari. Shots zote mbili hupigwa na zimeathiriwa kwenye uso wa ngazi. (a) kasi ya awali ya mpira kwenye shimo la pili ni nini? (b) kasi ya awali ya mpira kwenye shimo la nne ni nini? (c) Andika equation trajectory kwa kesi zote mbili. (d) Grafu trajectories.

Mkakati

Tunaona kwamba equation mbalimbali ina kasi ya awali na angle, hivyo tunaweza kutatua kwa kasi ya awali kwa wote (a) na (b). Tunapokuwa na kasi ya awali, tunaweza kutumia thamani hii kuandika equation trajectory.

Suluhisho

$R =\ frac {v_ {0} ^ {2}\ dhambi 2\ theta_ {0}} {g}\ Rightarrow v_ {0} =\ sqrt {\ dfrac {Rg} {\ dhambi 2\ theta_ {0}}} =\ sqrt {\ drac {(90.0\; m) (9.8\; m/s^ 2 {})} {\ dhambi (2 (30^ {o})}} = 31.9\; m/s $$
$R =\ frac {v_ {0} ^ {2}\ dhambi 2\ theta_ {0}} {g}\ Rightarrow v_ {0} =\ sqrt {\ dfrac {Rg} {\ dhambi 2\ theta_ {0}}} =\ sqrt {\ drac {(90.0\; m) (9.8\; m/s^ 2 {})} {\ dhambi (2 (70^ {o})}} = 37.0\; m/s $$
$$y = x\ Big [\ tan\ theta_ {0} -\ frac {g} {2 (v_ {0}\ cos\ theta_ {0}) ^ {2}} x\ Big] $$Shimo la pili: $$y = x\ Big [\ tan 30^ {o} -\ frac {9.8\; m/s^ {2}} {2}} {2} {(31.9\; m/s) (\ cos 30^ {o})] ^ {2}} x\ Big] = 0.58x - 0.0064x^ {2} $Shimo la nne: $$y = x\ Big [\ tan 70^ {o} -\ frac {9.8\; m/s^ {2}} {2}} {2}} {2} {2}} {2}} (37.0\; m/s) (\ cos 70^ {o})] ^ 2}} x\ Big] = 2 .75x - 0.0306x^ {2} $$
Kutumia matumizi ya graphing, tunaweza kulinganisha trajectories mbili, ambazo zinaonyeshwa kwenye Kielelezo$\PageIndex{6}$.

Kazi mbili za parabolic zinaonyeshwa. Aina ya trajectories zote mbili ni mita 90. Risasi moja husafiri juu sana kuliko nyingine. Risasi ya juu ina kasi ya awali ya mita 37 kwa pili na angle ya digrii 70. Risasi ya chini ina kasi ya awali ya mita 31.9 kwa pili na angle ya digrii 30. — Kielelezo$\PageIndex{6}$: Mbili trajectories ya mpira wa golf na aina mbalimbali ya 90 m. pointi athari ya wote ni katika ngazi sawa na hatua ya uzinduzi.

Umuhimu

Kasi ya awali ya risasi kwenye 70° ni kubwa kuliko kasi ya awali ya risasi kwenye 30°. Kumbuka kutoka Kielelezo$\PageIndex{6}$ kwamba projectiles mbili ilizindua kwa kasi sawa lakini kwa pembe tofauti na mbalimbali sawa kama uzinduzi pembe kuongeza 90°. Pembe za uzinduzi katika mfano huu zinaongeza kutoa idadi kubwa kuliko 90°. Hivyo, risasi katika 70° ina kuwa na kasi kubwa ya uzinduzi kufikia 90 m, vinginevyo ingeweza kutua kwa umbali mfupi.

Zoezi 4.4

Ikiwa shots mbili za golf katika Mfano 4.9 zilizinduliwa kwa kasi sawa, ambayo risasi ingekuwa na aina kubwa zaidi?

Tunaposema juu ya aina mbalimbali za projectile kwenye ardhi ya ngazi, tunadhani R ni ndogo sana ikilinganishwa na mzunguko wa Dunia. Kama, hata hivyo, mbalimbali ni kubwa, Dunia curves mbali chini ya projectile na kuongeza kasi kutokana na mvuto mabadiliko mwelekeo njiani. mbalimbali ni kubwa kuliko ilivyotabiriwa na equation mbalimbali aliyopewa mapema kwa sababu projectile ina mbali zaidi kuanguka kuliko ingekuwa juu ya kiwango cha chini, kama inavyoonekana katika Kielelezo$\PageIndex{7}$, ambayo ni msingi wa kuchora katika Principia Newton ya. Ikiwa kasi ya awali ni ya kutosha, projectile inakwenda kwenye obiti. Uso wa dunia hupungua m 5 kila m 8000 Katika 1 s kitu kinaanguka m 5 bila upinzani wa hewa. Hivyo, kama kitu kinapewa kasi ya usawa ya 8000 m/s (au 18,000 mi/hr) karibu na uso wa Dunia, itaingia katika obiti kuzunguka sayari kwa sababu uso unaendelea kuanguka mbali na kitu. Hii ni takribani kasi ya Kuhamisha Nafasi katika obiti ya chini ya Dunia wakati ilikuwa inafanya kazi, au satellite yoyote katika obiti ya chini ya Dunia. Mambo haya na mengine ya mwendo wa orbital, kama vile mzunguko wa Dunia, hufunikwa kwa kina zaidi katika Gravitation.

Takwimu inaonyesha kuchora ya dunia na mnara mrefu katika pole kaskazini na mshale usawa kinachoitwa v 0 akizungumzia haki. 5 trajectories zinazoanza juu ya mnara zinaonyeshwa. Wa kwanza hufikia dunia karibu na mnara. Ya pili hufikia dunia mbali na mnara, na ya tatu hata mbali zaidi. Trajectory ya nne inapiga dunia kwenye equator, na ni tangent kwa uso kwenye equator. Trajectory ya tano ni mzunguko unaozingatia dunia. — Kielelezo$\PageIndex{7}$: Projectile kwa satellite. Katika kila kesi iliyoonyeshwa hapa, projectile imezinduliwa kutoka mnara wa juu sana ili kuepuka upinzani wa hewa. Kwa kuongeza kasi ya awali, upeo huongezeka na kuwa mrefu zaidi kuliko ingekuwa kwenye ardhi ya ngazi kwa sababu Dunia inaondoka chini ya njia yake. Kwa kasi ya 8000 m/s, obiti inapatikana.

Masimulizi

Katika Phet Explorations: Projectile Motion, kujifunza kuhusu mwendo projectile katika suala la uzinduzi angle na kasi ya awali.