4.5: Mzunguko wa Mviringo Sare

Last updated
Save as PDF

Page ID: 176985

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Tatua kwa kasi ya centripetal ya kitu kinachohamia kwenye njia ya mviringo.
Tumia equations ya mwendo wa mviringo ili kupata msimamo, kasi, na kuongeza kasi ya chembe kutekeleza mwendo wa mviringo.
Eleza tofauti kati ya kuongeza kasi ya centripetal na kuongeza kasi ya tangential kutokana na mwendo usio wa kawaida wa mviringo.
Tathmini centripetal na tangential kuongeza kasi katika nonuniform mviringo mwendo, na kupata jumla kuongeza kasi vector.

Mzunguko wa mviringo wa kawaida ni aina maalum ya mwendo ambapo kitu kinasafiri kwenye mduara na kasi ya mara kwa mara. Kwa mfano, hatua yoyote juu ya propeller inazunguka kwa kiwango cha mara kwa mara ni kutekeleza mwendo sare mviringo. Mifano mingine ni ya pili, dakika, na saa mikono ya saa. Ni ajabu kwamba pointi juu ya vitu hivi kupokezana ni kweli kuongeza kasi, ingawa kiwango cha mzunguko ni mara kwa mara. Ili kuona hili, lazima tuchambue mwendo kwa suala la vectors.

Centripetal kuongeza kasi

Katika kinematics moja-dimensional, vitu vyenye kasi ya mara kwa mara vina kasi ya sifuri. Hata hivyo, katika kinematiki mbili na tatu-dimensional, hata kama kasi ni ya mara kwa mara, chembe inaweza kuwa na kasi ikiwa inakwenda pamoja na trajectory ya pembe kama vile mduara. Katika kesi hii vector kasi inabadilika, au\(\frac{d\vec{v}}{dt}\) ∙ 0. Hii inavyoonekana katika Kielelezo\(\PageIndex{1}\). Kama chembe inakwenda kinyume chake kwa wakati\(\Delta\) t kwenye njia ya mviringo, vector yake ya msimamo huenda kutoka\(\vec{r}(t)\) hadi\(\vec{r}(t + \Delta t)\). Vector kasi ina ukubwa wa mara kwa mara na ni tangent kwa njia kama inabadilika kutoka\(\vec{v}\) (t) hadi\(\vec{v}\left(t + \Delta t\right)\), kubadilisha mwelekeo wake tu. Kwa kuwa vector kasi\(\vec{v}(t)\) ni perpendicular kwa msimamo vector\(\vec{r}\) (t), pembetatu sumu na wadudu nafasi na\(\Delta \vec{r}\), na vectors kasi na\(\Delta \vec{v}\) ni sawa. Zaidi ya hayo, tangu

\[|\vec{r}(t) | = | \vec{r} (t + \Delta t)| \nonumber\]

\[| \vec{v} (t)| = | \vec{v} (t + \Delta t)|, \nonumber \]

pembetatu mbili ni isosceles. Kutokana na ukweli huu tunaweza kufanya madai

\[\dfrac{\Delta v}{v} = \dfrac{\Delta r}{r}\]

\[\Delta v = \dfrac{v}{r} \Delta r.\]

Kielelezo a inaonyesha mduara na kituo katika hatua C. sisi ni umeonyesha Radius r ya t na Radius r ya t, ambayo ni angle Delta theta mbali, na gumzo urefu delta r kuunganisha mwisho wa radii mbili. Vectors r ya t, r ya t plus delta t, na delta r kuunda pembetatu. Katika ncha ya vector r ya t, kasi inavyoonekana kama v ya t na pointi juu na kulia, tangent kwa mduara. Katika ncha ya vector r ya t plus delta t, kasi inavyoonekana kama v ya t plus delta t na pointi juu na kushoto, tangent kwa mduara. Kielelezo b inaonyesha wadudu v ya t na v ya t plus delta t na mikia yao pamoja, na vector delta v kutoka ncha ya v ya t kwa ncha ya v ya t plus delta t. wadudu hawa watatu kuunda pembetatu. Pembe kati ya v ya t na v ya t plus delta t ni theta. — Kielelezo\(\PageIndex{1}\): (a) chembe inahamia kwenye mduara kwa kasi ya mara kwa mara, na vectors nafasi na kasi wakati mwingine\(t\) na\(t + \Delta t\). (b) Vectors Velocity kutengeneza pembetatu. Pembetatu mbili katika takwimu ni sawa. Vector\(\Delta \vec{v}\) inaelezea kuelekea katikati ya mduara katika kikomo\(\Delta t → 0.\)

Tunaweza kupata ukubwa wa kuongeza kasi kutoka

\[a = \lim_{\Delta t \rightarrow 0} \left(\dfrac{\Delta v}{\Delta t}\right) = \frac{v}{r} \left(\lim_{\Delta t \rightarrow 0} \dfrac{\Delta r}{\Delta t}\right) = \frac{v^{2}}{r} \ldotp\]

Mwelekeo wa kuongeza kasi unaweza pia kupatikana kwa kutambua kwamba kama\(\Delta\) t na kwa hiyo\(\Delta \theta\) inakaribia sifuri, vector\(\Delta \vec{v}\) inakaribia mwelekeo perpendicular kwa\(\vec{v}\). Katika kikomo\(\Delta t → 0,\)\(\Delta \vec{v}\) ni perpendicular kwa\(\vec{v}\). Kwa kuwa\(\vec{v}\) ni tangent kwa mduara,\(\frac{d \vec{v}}{dt}\) pointi kasi kuelekea katikati ya mduara. Kuzingatia, chembe inayohamia kwenye mduara kwa kasi ya mara kwa mara ina kasi na ukubwa

\[a_{c} = \frac{v^{2}}{r} \ldotp \label{4.27}\]

Mwelekeo wa vector ya kuongeza kasi ni kuelekea katikati ya mduara (Kielelezo\(\PageIndex{2}\)). Hii ni kuongeza kasi ya radial na inaitwa kasi ya centripetal, ndiyo sababu tunaipa subscript\(c\). Neno centripetal linatokana na maneno ya Kilatini centrum (maana yake “katikati”) na petere (maana ya kutafuta”), na hivyo inachukua maana “kituo cha kutafuta.”

mduara ni umeonyesha kwa zambarau mshale kinachoitwa kama vector ndogo c akizungumzia radially ndani na kijani mshale tangent kwa mduara na kinachoitwa v. mishale ni inavyoonekana kwa mikia yao katika hatua moja juu ya mduara. — Kielelezo\(\PageIndex{2}\): Vector ya kuongeza kasi ya centripetal inaelezea kuelekea katikati ya njia ya mviringo ya mwendo na ni kuongeza kasi katika mwelekeo wa radial. Vector kasi pia inavyoonekana na ni tangent kwa mduara.

Hebu tuchunguze baadhi ya mifano inayoonyesha ukubwa wa jamaa wa kasi, radius, na kasi ya centripetal.

Mfano\(\PageIndex{1}\): Creating an Acceleration of 1 g

Ndege inaruka saa 134.1 m/s kando ya mstari wa moja kwa moja na hufanya kugeuka kwenye ngazi ya njia ya mviringo na ardhi. Je, radius ya mduara inapaswa kuzalisha kasi ya centripetal ya 1 g kwenye majaribio na ndege kuelekea katikati ya trajectory ya mviringo?

Mkakati

Kutokana na kasi ya ndege, tunaweza kutatua kwa radius ya mduara katika kujieleza kwa kasi ya centripetal.

Suluhisho

Weka kasi ya centripetal sawa na kasi ya mvuto: 9.8 m/s ² =\(\frac{v^{2}}{r}\).

Kutatua kwa radius, tunapata

\[r = \frac{(134.1\; m/s)^{2}}{9.8\; m/s^{2}} = 1835\; m = 1.835\; km \ldotp\]

Umuhimu

Ili kuongeza kasi zaidi kuliko g kwenye majaribio, ndege ingekuwa na kupungua kwa radius ya trajectory yake ya mviringo au kuongeza kasi yake kwenye trajectory yake iliyopo au wote wawili.

Zoezi 4.5

Flywheel ina radius ya cm 20.0. Je! Ni kasi gani ya hatua kwenye makali ya flywheel ikiwa inakabiliwa na kasi ya centripetal ya 900.0 cm/s ²?

Kuongeza kasi ya kasi inaweza kuwa na maadili mbalimbali, kulingana na kasi na radius ya curvature ya njia ya mviringo. Upeo wa kasi wa centripetal hutolewa katika Jedwali\(\PageIndex{1}\).

Jedwali\(\PageIndex{1}\): Upeo wa kawaida wa Centripetal
Kitu	Kuongezeka kwa kasi (m/s ² au sababu za g)
Dunia karibu na Jua	5.93 x 10 ^-3
Mwezi kuzunguka Dunia	2.73 x 10 ^-3
satellite katika obiti geosynchronous	0.233
Makali ya nje ya CD wakati wa kucheza	5.75
Jet katika roll ya pipa	(2-3 g)
Roller coaster	(5 g)
Electron inayozunguka protoni katika mfano rahisi wa Bohr wa atomi	9.0 x 10 ²²

Ulinganisho wa Mwendo kwa Mwendo wa Mviringo wa Sare

Chembe kutekeleza mwendo wa mviringo inaweza kuelezewa na vector yake ya msimamo\(\vec{r}(t)\). Kielelezo\(\PageIndex{3}\) kinaonyesha chembe kutekeleza mwendo mviringo katika mwelekeo kinyume. Kama chembe inakwenda kwenye mduara, vector yake ya msimamo inafuta angle\(\theta\) na x-axis. Vector\(\vec{r}(t)\) kufanya angle\(\theta\) na x-axis inavyoonekana na vipengele vyake pamoja na x- na y-axes. Ukubwa wa vector nafasi ni\(A = |\vec{r}(t)|\) na pia ni radius ya mduara, ili kwa suala la vipengele vyake,

\[\vec{r} (t) = A \cos \omega \hat{i} + A \sin \omega t \hat{j} \ldotp \label{4.28}\]

Hapa,\(\omega\) ni mara kwa mara inayoitwa mzunguko wa angular wa chembe. Mzunguko wa angular una vitengo vya radians (rad) kwa pili na ni idadi tu ya radians ya kipimo cha angular kwa njia ambayo chembe hupita kwa pili. Pembe\(θ\) ambayo vector nafasi ina wakati wowote ni\(\omega\) t.

Kama\(T\) ni kipindi cha mwendo, au wakati wa kukamilisha mapinduzi moja (\(2 \pi\, rad\)), basi

Radi ya mduara r, unaozingatia asili ya mfumo wa kuratibu x y inavyoonyeshwa. Radius r ya t ni vector kutoka asili hadi hatua kwenye mduara na iko kwenye pembe ya theta sawa na omega t kwa usawa. Sehemu x ya vector r ni ukubwa wa r ya t mara cosine ya omega t. y sehemu ya vector r ni ukubwa wa r ya t mara sine ya omega t. mzunguko ni kinyume chake kuzunguka mduara. — Kielelezo\(\PageIndex{3}\): Vector msimamo kwa chembe katika mwendo wa mviringo na vipengele vyake pamoja na x- na y-axes. Chembe huenda kinyume chake. Angle\(\theta\) ni mzunguko wa angular\(\omega\) katika radians kwa pili unaoongezeka kwa\(t\).

Velocity na kuongeza kasi inaweza kupatikana kutoka nafasi ya kazi kwa kutofautisha:

\[\vec{v} (t) = \frac{d \vec{r} (t)}{dt} = -A \omega \sin \omega t \hat{i} + A \omega \cos \omega t \hat{j} \ldotp \label{4.29}\]

Inaweza kuonyeshwa kutoka Kielelezo\(\PageIndex{3}\) kwamba vector kasi ni tangential kwa mduara katika eneo la chembe, na ukubwa A\(\omega\). Vile vile, vector ya kuongeza kasi inapatikana kwa kutofautisha kasi:

\[\vec{a} (t) = \frac{d \vec{v} (t)}{dt} = -A \omega^{2} \cos \omega t \hat{i} - A \omega^{2} \sin \omega t \hat{j} \ldotp \label{4.30}\]

Kutoka kwa usawa huu tunaona kwamba vector ya kuongeza kasi ina ukubwa A\(\omega^{2}\) na inaelekezwa kinyume na vector msimamo, kuelekea asili, kwa sababu\(\vec{a}\) (t) = -\(\omega^{2} \vec{r}\) (t).

Mfano\(\PageIndex{2}\): Circular Motion of a Proton

Proton ina kasi 5 x 10 ⁶ m/s na inahamia kwenye mduara katika ndege ya x ya radius r = 0.175 m Ni nafasi gani katika ndege ya xy wakati t = 2.0 x 10 ^-7 s = 200 ns? Katika t = 0, nafasi ya proton ni 0.175 m\(\hat{i}\) na inazunguka kinyume chake. Mchoro trajectory.

Suluhisho

Kutoka kwa data iliyotolewa, proton ina muda na mzunguko wa angular:

\[T = \frac{2 \pi r}{v} = \frac{2 \pi (0.175\; m)}{5.0 \times 10^{6}\; m/s} = 2.20 \times 10^{-7}\; s \nonumber \]

\[\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2.20 \times 10^{-7}\; s} = 2.856 \times 10^{7}\; rad/s \ldotp \nonumber \]

Msimamo wa chembe katika t = 2.0 x ^{10 -7} s na A = 0.175 m ni

\[\begin{align*} \vec{r} (2.0 \times 10^{-7}\; s) & = A \cos \omega (2.0 \times 10^{-7}\; s) \hat{i} + A \sin \omega (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{i} + 0.175 \sin (2.856 \times 10^{7}\; rad/s) (2.0 \times 10^{-7}\; s) \hat{j}\; m \\[4pt] & = 0.175 \cos (5.712\; rad) \hat{i} + 0.175 \sin (5.172\; rad) \hat{j}\; m \\ & = 0.147 \hat{i} - 0.095 \hat{j}\; m \ldotp \end{align*}\]

Kutokana na matokeo haya tunaona kwamba proton iko kidogo chini ya x-axis. Hii inavyoonekana katika Kielelezo\(\PageIndex{4}\).

Grafu ya nafasi y kama kazi ya nafasi ya x inavyoonyeshwa. Wote x na y hupimwa kwa mita na kukimbia kutoka -0.2 hadi 0.2. Proton inahamia kwenye mduara wa kinyume chake unaozingatia asili inavyoonyeshwa kwa nyakati 11 tofauti. Katika t = 0 s chembe iko katika x = 0.175 m na y = 0. Katika t = 200 nanoseconds, chembe iko katika nafasi iliyotolewa na vector 0.147 I kofia minus 0.95 j mita kofia. — Kielelezo\(\PageIndex{4}\): Nafasi vector ya proton katika\(t = 2.0 \times 10^{−7}\,ms = 200\, ns\). Trajectory ya proton inavyoonyeshwa. Pembe ambayo proton husafiri kando ya mduara ni 5.712 rad, ambayo kidogo chini ya moja mapinduzi kamili.

Umuhimu

Tulichukua nafasi ya awali ya chembe kuwa kwenye x-axis. Hii ilikuwa kiholela kabisa. Ikiwa nafasi tofauti ya kuanzia ilitolewa, tutakuwa na nafasi tofauti ya mwisho katika t = 200 ns.

Mzunguko usio wa kawaida wa mviringo

Mzunguko wa mviringo haipaswi kuwa kasi ya mara kwa mara. Chembe inaweza kusafiri katika mduara na kuharakisha au kupunguza kasi, kuonyesha kasi katika mwelekeo wa mwendo.

Katika mwendo wa mviringo sare, chembe inayofanya mwendo wa mviringo ina kasi ya mara kwa mara na mduara iko kwenye radius iliyowekwa. Ikiwa kasi ya chembe inabadilika pia, basi tunaanzisha kasi ya ziada katika mwelekeo tangential kwa mduara. Accelerations vile kutokea katika hatua juu kwamba ni kubadilisha kiwango chake spin, au rotor yoyote ya kuongeza kasi. Katika Uhamisho na Vectors Velocity tulionyesha kuwa kasi ya centripetal ni kiwango cha wakati wa mabadiliko ya mwelekeo wa vector kasi. Ikiwa kasi ya chembe inabadilika, basi ina kasi ya tangential ambayo ni kiwango cha wakati wa mabadiliko ya ukubwa wa kasi:

\[a_{T} = \frac{d |\vec{v}|}{dt} \ldotp \label{4.31}\]

Mwelekeo wa kuongeza kasi ya tangential ni tangent kwa mduara ambapo mwelekeo wa kasi ya centripetal ni radially ndani kuelekea katikati ya mduara. Hivyo, chembe katika mwendo wa mviringo na kuongeza kasi ya tangential ina kuongeza kasi ya jumla ambayo ni jumla ya vector ya kasi ya centripetal na tangential:

\[\vec{a} = \vec{a}_{c} + \vec{a}_{T} \ldotp \label{4.32}\]

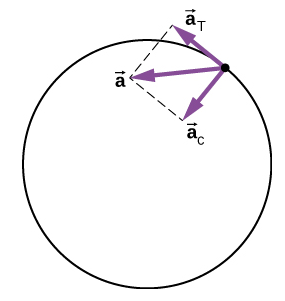
Vectors kuongeza kasi ni inavyoonekana katika Kielelezo\(\PageIndex{5}\). Kumbuka kwamba vectors mbili kuongeza kasi\(\vec{a}_{c}\) na\(\vec{a}_{T}\) ni perpendicular kwa kila mmoja, na\(\vec{a}_{c}\) katika mwelekeo radial na\(\vec{a}_{T}\) katika mwelekeo tangential. \(\vec{a}\)pointi jumla ya kuongeza kasi kwa pembe kati\(\vec{a}_{c}\) na\(\vec{a}_{T}\).

Kuongezeka kwa chembe kwenye mduara huonyeshwa pamoja na vipengele vyake vya radial na tangential. Kuongeza kasi ya centripetal pointi ndogo c radially kuelekea katikati ya mduara. Kuongeza kasi ya tangential ndogo T ni tangential kwa mduara katika nafasi ya chembe. Kuongeza kasi ya jumla ni jumla ya vector ya kasi ya kasi ya tangential na centripetal, ambayo ni perpendicular. — Kielelezo\(\PageIndex{5}\): Kuongeza kasi ya centripetal kuelekea katikati ya mduara. Kuongeza kasi ya tangential ni tangential kwa mduara katika nafasi ya chembe. Kuongeza kasi ya jumla ni jumla ya vector ya kasi ya kasi ya tangential na centripetal, ambayo ni perpendicular.

Mfano\(\PageIndex{3}\): Total Acceleration during Circular Motion

Chembe inakwenda kwenye mduara wa radius r = 2.0 m Wakati wa muda kutoka t = 1.5 s hadi t = 4.0 s kasi yake inatofautiana na wakati kulingana na

\[v(t) = c_{1} - \frac{c_{2}}{t^{2}}, c_{1} = 4.0\; m/s, c_{2} = 6.0\; m \cdotp s \ldotp\]

Je, ni kuongeza kasi ya jumla ya chembe saa t = 2.0 s?

Mkakati

Tunapewa kasi ya chembe na radius ya mduara, hivyo tunaweza kuhesabu kasi ya centripetal kwa urahisi. Mwelekeo wa kasi ya centripetal ni kuelekea katikati ya mduara. Tunapata ukubwa wa kuongeza kasi ya tangential kwa kuchukua derivative kwa heshima ya wakati wa |v (t) | kutumia Equation\ ref {4.31} na kutathmini kwa t = 2.0 s Tunatumia hii na ukubwa wa kasi ya centripetal ili kupata kasi ya jumla.

Suluhisho

Centripetal kuongeza kasi ni

\[v(2.0\; s) = \left(4.0 - \dfrac{6.0}{(2.0)^{2}}\right) m/s = 2.5\; m/s \nonumber \]

\[a_{c} = \frac{v^{2}}{r} = \frac{(2.5\; m/s)^{2}}{2.0\; m} = 3.1\; m/s^{2} \nonumber \]

kuelekezwa kuelekea katikati ya mduara. Tangential kuongeza kasi ni

\[a_{T} = \Big| \frac{d \vec{v}}{dt} \Big| = \frac{2 c_{2}}{t^{3}} = \frac{12.0}{(2.0)^{3}} m/s^{2} = 1.5\; m/s^{2} \ldotp \nonumber \]

Jumla ya kuongeza kasi ni

\[|\vec{a}| = \sqrt{3.1^{2} + 1.5^{2}} m/s^{2} = 3.44\; m/s^{2}\]

na\(\theta\) = ^{tan -1}\(\left(\dfrac{3.1}{1.5}\right)\) = 64° kutoka tangent hadi mduara. Angalia Kielelezo\(\PageIndex{6}\).

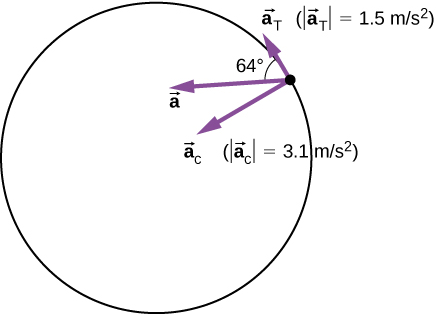
ALT="Kasi ya chembe kwenye mduara inaonyeshwa pamoja na sehemu zake za radial na tangential. Kuongeza kasi ya centripetal ndogo c inaelezea radially kuelekea katikati ya mduara na ina ukubwa mita 3.1 kwa mraba wa pili. Kuongeza kasi ya tangential ndogo T ni tangential kwa mduara katika nafasi ya chembe na ina ukubwa wa mita 1.5 kwa mraba wa pili. Pembe kati ya kuongeza kasi ya jumla na kasi ya tangential ndogo T ni digrii 64.” — Kielelezo\(\PageIndex{6}\): Vectors tangential na centripetal kuongeza kasi. Kuongeza kasi ya wavu\(\vec{a}\) ni jumla ya vector ya kasi mbili.

Umuhimu

Maelekezo ya kasi ya centripetal na tangential yanaweza kuelezewa kwa urahisi zaidi kwa suala la mfumo wa kuratibu wa polar, na vectors ya kitengo katika maelekezo ya radial na tangential. Mfumo huu wa kuratibu, ambao hutumiwa kwa mwendo pamoja na njia za mviringo, unajadiliwa kwa undani baadaye katika kitabu.